
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Дипломная работа: Модель портального манипулятора
Дипломная работа: Модель портального манипулятора
Построение и исследование динамической модели портального манипулятора
Аннотация
Данная работа посвящена построению и исследованию динамической модели портального манипулятора, описывающей переходные процессы в манипуляторе с шаговым приводом в момент его позиционирования. При построении были использованы экспериментально полученные параметры, благодаря чему удалось получить достаточно простую и адекватную модель.
При составлении подобных моделей у разработчика возникает стремление как можно более полно отразить свойства и характеристики объекта, что приводит к чрезмерному росту сложности модели, в результате чего снижается ее практическая полезность. Поэтому в данной работе особое внимание уделено разумному упрощению модели, а также возможности ее практического использования.
В ходе исследования полученной модели решена задача выбора оптимальной скорости перемещения рабочего органа, определена степень влияния точности позиционирования на быстродействие манипулятора.
Полученные результаты исследований могут быть использованы при проектировании новых и эксплуатации имеющихся моделей манипуляторов для определения рациональных значений динамических параметров.
Введение
Для решения задачи выбора оптимальной скорости перемещения звеньев манипулятора с шаговым двигателем, с целью увеличения его быстродействия, необходимо учитывать переходные процессы возникающие при позиционировании рабочих органов. Переходные процессы в виде затухающих механических колебаний возникают под действием инерционных нагрузок и приводят к увеличению времени позиционирования при выполнении переходов технологического процесса, например, при сборке, сверлении, контроле и др. Для планирования траектории необходимо знать время затухания колебаний до значения допустимой погрешности позиционирования, при котором рабочий орган манипулятора может продолжать движение. С целью определения времени такого переходного процесса создана модель манипулятора портального типа с консольной подвижной частью.
Моделирование динамики манипулятора
Методы построения динамической модели манипулятора
Динамическая модель манипулятора может быть построена на основе использования известных законов ньютоновской или лагранжевой механики. Результатом применения этих законов являются уравнения, связывающие действующие в сочленениях силы и моменты с кинематическими характеристиками и параметрами движения звеньев. Таким образом, уравнения динамики движения реального манипулятора могут быть получены традиционными методами Лагранжа – Эйлера или Ньютона – Эйлера. С помощью этих двух методов получен ряд различных форм уравнения движения, эквивалентных в том смысле, что они описывают динамику движения одной и той же физической системы.
Вывод уравнений динамики движения манипулятора методом Лагранжа – Эйлера отличается простотой и единством подхода. В рамках предположения о том, что звенья представляют собой твердые тела, этот подход приводит в общем случае к системе нелинейных дифференциальных уравнений второго порядка. Уравнения Лагранжа – Эйлера обеспечивают строгое описание динамики состояния манипулятора и могут быть использованы для разработки усовершенствованных законов управления в пространстве присоединенных переменных. В меньшей степени они используются для решения прямой и обратной задач динамики. Прямая задача состоит в том, чтобы по заданным силам и моментам определить обобщенные ускорения, интегрирование которых позволяет получить значения обобщенных координат и скоростей. Обратная задача динамики заключается в том, чтобы по заданным обобщенным координатам, скоростям и ускорениям определить действующие в сочленениях манипулятора силы и моменты.
С целью получения более эффективных с вычислительной точки зрения алгоритмов можно использовать уравнения Ньютона – Эйлера. Вывод уравнений движения манипулятора методом Ньютона – Эйлера прост по содержанию, но весьма трудоемок. Результатом является система прямых и обратных рекуррентных уравнений, последовательно применяемых к звеньям манипулятора. С помощью прямых уравнений последовательно от основания к схвату вычисляются кинематические характеристики движения звеньев, такие, как линейные и угловые скорости и ускорения, линейные ускорения центров масс звеньев. Обратные уравнения позволяют последовательно от схвата к основанию вычислить силы и моменты, действующие на каждое из звеньев. Наиболее важный результат такого подхода состоит в том, что время, необходимое для вычисления обобщенных сил и моментов прямо и пропорционально числу сочленений, но не зависит от реализующейся в процессе движения конфигурации манипулятора. Это позволяет реализовывать простые законы управления манипулятором в реальном времени.
Низкая вычислительная эффективность уравнений Лагранжа – Эйлера обусловлена в основном тем, что для описания кинематической цепи используются матрицы преобразования однородных координат. Уравнения Ньютона – Эйлера обладают большей вычислительной эффективностью, что связано с их рекуррентной природой. Однако такие рекуррентные уравнения не обладают “аналитичностью”, столь полезной при синтезе управления в пространстве состояний. Для синтеза законов управления желательно иметь в распоряжении замкнутую систему дифференциальных уравнений, точно описывающих динамику движения манипулятора.
В связи с тем что для построения модели динамики переходных процессов и дальнейшего анализа полученных уравнений необходима аналитическая форма, решено использовать для получения уравнений динамики метод Лагранжа – Эйлера.
Уравнения динамики манипулятора
Уравнения Лагранжа второго рода для голономной системы с n степенями свободы, которым отвечают обобщенные координаты ![]() (j = 1,2,…,n), имеют вид
(j = 1,2,…,n), имеют вид
|
|
(1.1) |
где ![]() – функция Лагранжа, разности кинетической Т и потенциальной П энергий системы;
– функция Лагранжа, разности кинетической Т и потенциальной П энергий системы; ![]() – обобщенные силы управляющих приводов, приведенные к j-ой обобщенной координате: они имеют размерность моментов, если
– обобщенные силы управляющих приводов, приведенные к j-ой обобщенной координате: они имеют размерность моментов, если ![]() – угол поворота, или сил, если
– угол поворота, или сил, если ![]() – линейное перемещение.
– линейное перемещение.
С учетом того, что ![]() и
и ![]() , перепишем уравнение (1.1) в виде
, перепишем уравнение (1.1) в виде
|
|
(1.2) |
где ![]() ,
, ![]() .
.
В последних равенствах через ![]() обозначены внешние обобщенные силы, вызванные весом звеньев и груза, удерживаемого в захватном устройстве. При наличии внешнего воздействия – силы
обозначены внешние обобщенные силы, вызванные весом звеньев и груза, удерживаемого в захватном устройстве. При наличии внешнего воздействия – силы ![]() , приложенной к захватному устройству, в правую часть равенства для
, приложенной к захватному устройству, в правую часть равенства для ![]() надо добавить член
надо добавить член ![]() , характеризующий это воздействие:
, характеризующий это воздействие:
|
|
(1.3) |
Используем выражение (1.2) для вывода уравнений динамики манипулятора. Рассматривая исполнительный механизм манипулятора как систему из n твердых тел, запишем его кинетическую энергию T в виде суммы кинетических энергий звеньев:
|
|
(1.4) |
В свою очередь величину ![]() определим по формуле [3]
определим по формуле [3]
|
|
(1.5) |
где ![]() – масса звена i;
– масса звена i; ![]() – скорость некоторой точки звена
– скорость некоторой точки звена ![]() , принятой за полюс;
, принятой за полюс; ![]() – вектор радиус центра инерции звена в системе осей с ним связанных, начало которой совпадает с полюсом
– вектор радиус центра инерции звена в системе осей с ним связанных, начало которой совпадает с полюсом ![]() ;
; ![]() – тензор инерции звена в точке
– тензор инерции звена в точке ![]() ;
; ![]() – вектор угловой скорости звена в принятой системе координат.
– вектор угловой скорости звена в принятой системе координат.
Выражение (1.5) принимает наиболее простой вид, если за полюс звена принять его центр инерции; величина ![]() будет равна нулю и выражение (1.5) упростится:
будет равна нулю и выражение (1.5) упростится:
|
|
(1.6) |
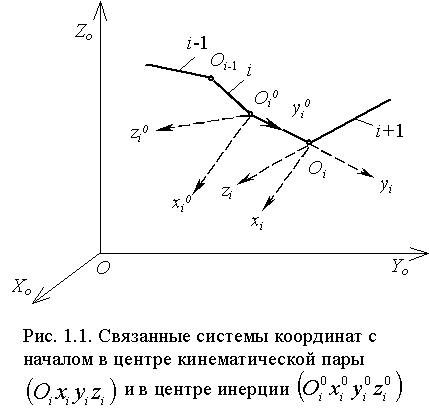
Кроме того, в большинстве случаев звенья манипулятора представляют собой твердые тела, обладающие симметрией относительно трех ортогональных осей, проведенных через центр инерции. Напомнив правило разметки осей систем координат, связанных со звеньями, в соответствии с которым одна из осей системы ![]() совпадает с осью звена (вектором
совпадает с осью звена (вектором ![]() ), а две другие образуют с ней правую триаду, получим при помещении точки
), а две другие образуют с ней правую триаду, получим при помещении точки ![]() в центр инерции
в центр инерции ![]() (см. рис. 1.1) оси полученной системы
(см. рис. 1.1) оси полученной системы ![]() становятся главными осями инерции и тензор вектора в точке
становятся главными осями инерции и тензор вектора в точке ![]() имеет вид диагональной матрицы
имеет вид диагональной матрицы
|
|
(1.7) |
моменты инерции относительно осей в которой определяются выражениями
|
|
(1.8) |
и для звеньев заданной конфигурации являются известными константами. При отсутствии осевых симметрий тензор инерции звена в точке ![]() характеризуется матрицей
характеризуется матрицей
|
|
(1.9) |
центробежные моменты в которой определяются выражениями
|
|
(1.10) |
и также являются известными константами.
Определим вектор скорости центра инерции звена i через проекции на оси связанной с ним системы координат как
|
|
(1.11) |
или через проекции на оси неподвижной системы осей в виде
|
|
(1.12) |
По аналогии с ![]() введем вектор угловой скорости звена
введем вектор угловой скорости звена
|
|
(1.13) |
и запишем равенство (1.6) в развернутой форме для случая, когда звенья манипулятора обладают симметрией относительно главных осей инерции. Для этого подставим выражения ![]() ,
, ![]() ,
, ![]() из (1.7), (1.11), (1.13) в (1.6) и получим
из (1.7), (1.11), (1.13) в (1.6) и получим
|
|
(1.14) |
При использовании вектора скорости центра инерции в форме (1.14) выражение
|
|
(1.15) |
с учетом которого равенство (1.4) принимает вид
|
|
(1.16) |
Построение динамической модели переходных процессов манипулятора МРЛ-901П
Модель переходных процессов в манипуляторе МРЛ-901П
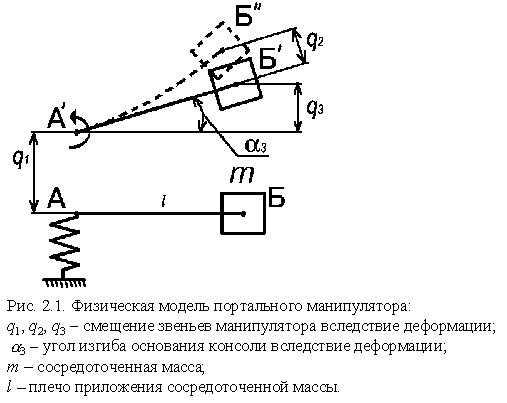
Модель портального манипулятора МРЛ-901П представлена на рис. 2.1. Деформирующимися элементами в манипуляторе являются: зубчатый ремень, обозначенный пружиной; консольная часть, на которой имеется сосредоточенная масса m. Деформация поперечной консоли обозначена на схеме углом ![]() . Исходными данными для расчета такой модели будут: значение подвижной массы m, плечо приложения этой массы l, а также коэффициент натяжения зубчатого ремня, определяемый как отношение прогиба ремня к его длине и влияющий на жесткость, и демпфирование модуля линейного перемещения.
. Исходными данными для расчета такой модели будут: значение подвижной массы m, плечо приложения этой массы l, а также коэффициент натяжения зубчатого ремня, определяемый как отношение прогиба ремня к его длине и влияющий на жесткость, и демпфирование модуля линейного перемещения.
При остановке электроприводов подвижные массы будут продолжать движение под действием инерционных сил, в результате чего точки А и Б займут положение ![]() и
и ![]() соответственно, затем остановятся и под действием сил упругой деформации пружины и балки начнут совершать колебательное движения.
соответственно, затем остановятся и под действием сил упругой деформации пружины и балки начнут совершать колебательное движения.
Рассматриваемая модель имеет три степени свободы, обозначим независимые обобщенные координаты как ![]() ,
, ![]() и
и ![]() . Для описания данной модели воспользуемся уравнением Лагранжа второго рода:
. Для описания данной модели воспользуемся уравнением Лагранжа второго рода:
|
|
(2.1) |
где T - кинетическая энергия системы; Q - обобщенная сила; k - количество степеней свободы.
Кинетическая энергия системы с тремя степенями свободы является однородной квадратичной формой обобщенных скоростей [5]:
|
|
(2.2) |
Коэффициенты ![]() являются функциями координат
являются функциями координат ![]() ,
, ![]() и
и ![]() .
.
Предположим, что обобщенные координаты отсчитываются от положения равновесия, где ![]() .
.
Располагая коэффициенты ![]() по степеням и пологая для упрощения записи
по степеням и пологая для упрощения записи ![]() , получим:
, получим:
|
|
(2.3) |
Потенциальная энергия ![]() системы:
системы:
|
|
(2.4) |
При этом учитываем, что в положении равновесия ![]() обобщенные силы также обращаются в нуль.
обобщенные силы также обращаются в нуль.
В (2.4) для упрощения приняты следующие обозначения:
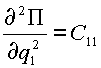 ,
, 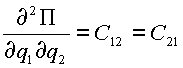 ,
, 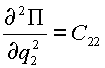 ,
, 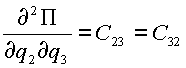 ,
, 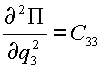 ,
, 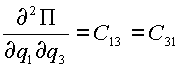 .
.
Для составления дифференциальных уравнений свободных колебаний в форме уравнений Лагранжа второго рода, выразим потенциальную энергию через обобщенные координаты. Рассмотрим равновесие системы, на которую действуют силы ![]()
![]() …,
…,![]() . Потенциальная энергия в состоянии устойчивого равновесия имеет минимум, равный нулю, а при вызванном действием сил
. Потенциальная энергия в состоянии устойчивого равновесия имеет минимум, равный нулю, а при вызванном действием сил ![]() отклонении от него выражается квадратичной формой вида (2.4).
отклонении от него выражается квадратичной формой вида (2.4).
Элементарная работа всех сил действующих на систему, по принципу возможных перемещений должна быть равна нулю:
|
|
(2.5) |
Замечая, что
|
|
а также приравнивая к нулю коэффициенты при независимых вариациях ![]() ,
, ![]() и
и ![]() , получаем три уравнения:
, получаем три уравнения:
|
|
(2.6) |
Здесь ![]() ,
, ![]() и
и ![]() -
обобщенные силы для системы сил
-
обобщенные силы для системы сил ![]()
![]() …,
…,![]() , уравновешивающих потенциальные силы, возникающие при отклонении системы из положения равновесия
, уравновешивающих потенциальные силы, возникающие при отклонении системы из положения равновесия ![]() . Заменяя в (2.6) производные потенциальной энергии их выражениями согласно (2.4), получим систему уравнений, определяющих значение координат
. Заменяя в (2.6) производные потенциальной энергии их выражениями согласно (2.4), получим систему уравнений, определяющих значение координат ![]() ,
, ![]() и
и ![]() в положении равновесия:
в положении равновесия:
|
|
(2.7) |
причем ![]() ,
, ![]() и
и ![]() .
.
Решение системы (2.7) имеет вид:
|
|
(2.8) |
где
|
|
(2.9) |
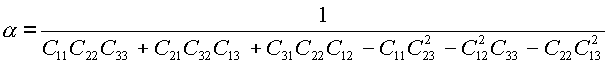 .
.
На систему действуют обобщенные силы, которыми являются инерционные силы и силы сопротивления движению. Обычно в сложных системах в целях упрощения [4, 5] силу сопротивления принимают пропорциональной первой степени скорости движения. С целью упрощения условимся, что угол ![]() мал и координаты массы m можно записать как
мал и координаты массы m можно записать как ![]() . Поэтому на основании кинетостатики можем записать:
. Поэтому на основании кинетостатики можем записать:
|
|
(2.10) |
где ![]() -
обобщенная сила,
-
обобщенная сила, ![]() -
коэффициент сопротивления пропорциональный первой степени скорости движения массы m. Так как масса собственно консоли манипулятора МРЛ-901П меньше массы закрепленных на ней рабочих головок, захватов и деталей, для упрощения примем условие, что точка исследования колебаний (практически -
рабочий орган манипулятора) совпадает с точкой приложения сосредоточенной массы m.
-
коэффициент сопротивления пропорциональный первой степени скорости движения массы m. Так как масса собственно консоли манипулятора МРЛ-901П меньше массы закрепленных на ней рабочих головок, захватов и деталей, для упрощения примем условие, что точка исследования колебаний (практически -
рабочий орган манипулятора) совпадает с точкой приложения сосредоточенной массы m.
Сила ![]() действует на все звенья манипулятора следовательно:
действует на все звенья манипулятора следовательно:
|
|
(2.11) |
Коэффициенты ![]() в (2.7) будем определять из того, что согласно (2.11) звенья можно рассматривать независимо друг от друга. Положим сначала, что
в (2.7) будем определять из того, что согласно (2.11) звенья можно рассматривать независимо друг от друга. Положим сначала, что ![]() действует только по координате
действует только по координате ![]() , затем только по координате
, затем только по координате ![]() и наконец только по координате
и наконец только по координате ![]() , тогда в выражение (2.7) можно переписать:
, тогда в выражение (2.7) можно переписать:
|
|
(2.12) |
таким образом ![]() , используя (2.9) находим:
, используя (2.9) находим:
|
|
(2.13) |
Коэффициенты ![]() ,
, ![]() и
и ![]() определяют податливость звеньев манипулятора по координатам
определяют податливость звеньев манипулятора по координатам ![]() ,
, ![]() и
и ![]() соответственно. Выражая податливость звеньев через их жесткость, запишем:
соответственно. Выражая податливость звеньев через их жесткость, запишем:
|
|
(2.14) |
где ![]() ,
, ![]() и
и ![]() жесткости звеньев по координатам
жесткости звеньев по координатам ![]() ,
, ![]() и
и ![]() соответственно.
соответственно.
Подставляя (2.14) , (2.11) и (2.10) в (2.8) получим:
|
|
(2.15) |
Для решения этой системы нужно выразить скорость и ускорение массы m через их составляющие:
|
|
(2.16) |
Поскольку в манипуляторе суммарную жесткость удобно экспериментально определять, прикладывая соответствующее усилие к его рабочему органу, и так как в конечном итоге необходимо определить положение массы m, координаты которой выражаются как ![]() , то для этого достаточно сложить уравнения в выражении (2.15):
, то для этого достаточно сложить уравнения в выражении (2.15):
|
|
(2.17) |
или:
|
|
(2.18) |
где С - суммарная жесткость звеньев манипулятора.
Анализ показывает, что величина C является переменной и зависит от плеча приложения l сосредоточенной массы m.
Преобразуя (2.18), получаем уравнение описывающие переходный процесс в системе:
|
|
(2.19) |
Уравнение (2.19) легко решается классическим способом при следующих начальных условиях:
|
|
(2.20) |
где ![]() - скорость рабочего органа манипулятора в момент выхода на конечную точку.
- скорость рабочего органа манипулятора в момент выхода на конечную точку.
Выражение (2.19) представляет собой линейное дифференциальное уравнение второго порядка. Будем искать частное решение уравнения в виде:
|
|
(2.21) |
где ![]() и
и ![]() -
произвольные постоянные, которые могут быть определены из начальных условий: при t = 0;
-
произвольные постоянные, которые могут быть определены из начальных условий: при t = 0; ![]() и
и ![]() -
корни характеристического уравнения:
-
корни характеристического уравнения:
|
|
(2.22) |
Решение уравнения (2.22) будет иметь вид:
|
|
(2.23) |
Определим произвольные постоянные ![]() и
и ![]() , решая систему уравнений:
, решая систему уравнений:
|
|
(2.24) |
Решение системы (2.24) будет иметь вид:
|
|
(2.25) |
если учесть (2.20) то:
|
|
(2.26) |
подставляя (2.26) в (2.21) и с учетом (2.23) имеем:
|
|
(2.27) |
где 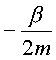 -
реальная часть;
-
реальная часть; 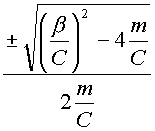 -
мнимая часть.
-
мнимая часть.
Тогда разделяя реальную и мнимую части в (2.27) получим:
|
|
(2.28) |
Учитывая что:
|
|
(2.29) |
имеем:
|
|
(2.30) |
Преобразуя (2.30) получим решение уравнения (2.19):
|
|
(2.31) |
Прологарифмируем выражение (2.31) предварительно подставив в него значение допустимой погрешности позиционирования:
|
|
(2.32) |
где ![]() -
допустимая погрешность позиционирования.
-
допустимая погрешность позиционирования.
Преобразуя (2.32) получим выражение для определения времени переходного процесса:
|
|
(2.33) |
Для расчета жесткости C и коэффициента демпфирования ![]() в модели используются экспериментально полученные зависимости. В частности коэффициент демпфирования определяется по осциллограмме затухания колебаний рабочего органа.
в модели используются экспериментально полученные зависимости. В частности коэффициент демпфирования определяется по осциллограмме затухания колебаний рабочего органа.
Таким образом, время переходного процесса, для данного типа манипулятора при заданной массе положении рабочего органа определяется по выражению (2.33), в котором коэффициенты жесткости и демпфирования предварительно определены экспериментально.
2.2 Анализ переходных процессов в манипуляторе МРЛ-901П
Источниками возникновения переходных процессов в манипуляторе МРЛ-901П являются: зубчатая ременная передача линейного модуля манипулятора и его свободная консоль.
На этапе зондирующих экспериментов исследовались парные зависимости коэффициента демпфирования от натяжения зубчатого ремня и смещения рабочего органа вдоль консоли. Результаты анализа полученных осциллограмм сведены в таблицы 2.1 и 2.2.
Анализ результатов показывает, что натяжение зубчатого ремня существенным образом влияет на коэффициенты демпфирования модуля линейного перемещения: так при увеличении начального натяжения ремня от минимального значения h = 0,03778 до максимального h = 0,00667 (в исследуемых приделах) коэффициент демпфирования уменьшается в 3 раза. Таким образом, можно сделать вывод о том, что демпфирование линейного модуля с зубчатой ременной передачей может задаваться и варьироваться в широких пределах, как на этапе конструирования, так и в процессе его эксплуатации.
|
Табл. 2.1 |
|||||
|
Результаты анализа осциллограмм собственных колебаний рабочего органа манипулятора МРЛ-901П на консоли |
|||||
|
Величина смещения рабочего органа вдоль консоли ly, мм |
Период колебаний рабочего органа T, с. |
Частота колебаний w, с-1 |
Логарифмический декремент затухания n |
Коэффициент демпфирования b, кг/c |
Время затухания колебаний tп.п., с. |
|
0 |
0,057 |
17,54 |
0,956 |
369 |
0,6 |
|
175 |
0,067 |
15 |
0,693 |
227,55 |
0,9 |
|
350 |
0,08 |
12,5 |
0,446 |
122,65 |
1,2 |
Анализ результатов исследований показывает, что смещение рабочего органа манипулятора МРЛ-901П вдоль свободной консоли, также как и увеличение начального натяжения ремня, вызывает уменьшение коэффициентов демпфирования, что существенно (в 2…3 раза) увеличивает время полного затухания собственных колебаний рабочего органа (см. табл. 2.1 и 2.2), и, как следствие снижает реальную производительность.
Смещение рабочего органа относительно основания и увеличение натяжения ремня приводит также к уменьшению частоты собственных колебаний манипулятора, что должно учитываться при использовании его в технологических процессах, связанных с резонансными явлениями.
Комплексные исследования демпфирующих свойств манипулятора осуществлялись с целью установления численной зависимости коэффициента демпфирования от величины начального натяжения ремня и смещения рабочего органа вдоль консоли. В качестве функции отклика выбиралась линейная модель. База данных для построения плана экспериментов сведена в табл. 2.
Основные уровни и интервалы варьирования выбирались на основе результатов зондирующих экспериментов, а также исследований жесткости и точносных параметров манипулятора МРЛ-901П.
|
Табл. 2.3 |
||||
|
База данных для построения плана экспериментов |
||||
|
Наименование фактора |
Условное обозначение |
Область определения |
Основной уровень |
Интервал варьирования |
|
Начальное натяжение ремня h |
X1 |
0...0,04 |
0,02 |
0,013 |
|
Величина смещения рабочего органа манипулятора вдоль консоли ly, мм |
X2 |
0...350 |
175 |
175 |
Матрица планирования и результаты экспериментов сведены в табл. 2.4.
Проводилась полная статистическая обработка результатов экспериментов, позволившая получить адекватную модель зависимости коэффициентов демпфирования от исследуемых факторов в виде:
|
|
(2.34) |
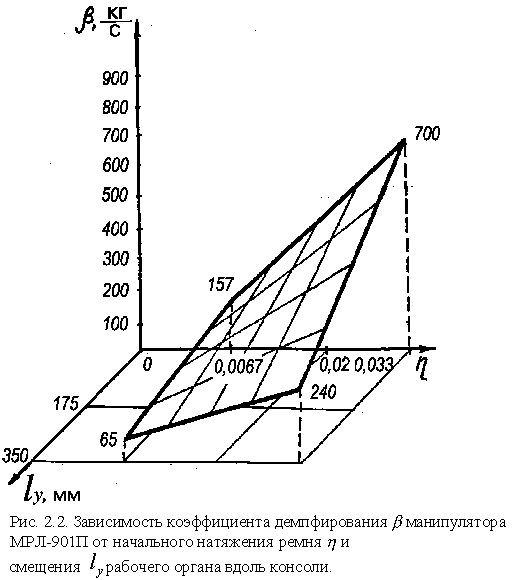
Поверхность отклика представлена на рис. 2.2. Выражение (2.34) позволяет получить численное значение коэффициента демпфирования, необходимое для расчета продолжительности переходного процесса при позиционировании.
|
Табл. 2.4 |
||||||||
|
Матрица планирования и результатов экспериментов по комплексному исследованию демпфирующих свойств манипулятора МРЛ-901П |
||||||||
|
Номер опыта |
|
|
|
|
Среднее значение коэффициента демпфирования, кг/c |
Дисперсия среднего арифметического |
Вычисленное значение |
|
|
1 |
+1 |
+1 |
+1 |
+1 |
240 |
64 |
240 |
|
|
2 |
+1 |
+1 |
-1 |
-1 |
700 |
49 |
700 |
|
|
3 |
+1 |
-1 |
+1 |
-1 |
65 |
4 |
65 |
|
|
4 |
+1 |
-1 |
-1 |
+1 |
157 |
16 |
157 |
|
Экспериментальные исследования времени переходного процесса осуществлялись при помощи комплекта виброизмерительной аппаратуры АВ-44, вибродатчик которой крепился на рабочем органе манипулятора.
2.3 Определение жесткости звеньев манипулятора МРЛ-901П
Жесткость звеньев манипулятора МРЛ-901П определялась по экспериментальным замерам деформации консоли манипулятора при действии на нее определенного усилия.
|
Таблица 2.5 |
||||
|
Деформация звеньев манипулятора МРЛ-901П под действием возмущающих сил |
||||
|
Возму- щающая сила |
Деформация звеньев манипуляционной системы d, мм |
|||
|
Ось X |
Ось Y |
|||
|
Y=0 |
|
|
||
|
0 |
0 |
0 |
0 |
0 |
|
10 |
0,111 |
0,135 |
0,178 |
0,111 |
|
20 |
0,206 |
0,234 |
0,390 |
0,206 |
|
30 |
0,265 |
0,334 |
0,560 |
0,265 |
|
40 |
0,302 |
0,418 |
0,750 |
0,302 |
|
50 |
0,345 |
0,507 |
0,930 |
0,348 |
|
60 |
0,390 |
0,580 |
1,090 |
0,393 |
|
70 |
0,418 |
0,658 |
0,421 |
|
|
80 |
0,460 |
0,745 |
0,465 |
|
|
90 |
0,498 |
0,825 |
0,505 |
|
|
100 |
0,534 |
0,902 |
0,540 |
|
Результаты исследования жесткости приведены в таблице 2.5. По этим данным были построены график зависимости деформации от смещения рабочего органа (рис. 2.3) и график зависимости деформации от натяжения зубчатого ремня (рис.2.4).
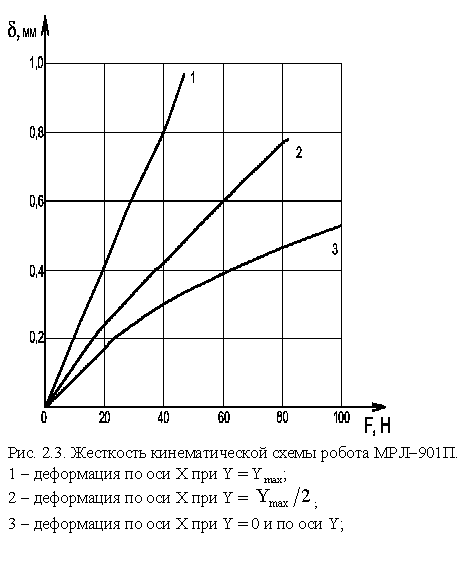
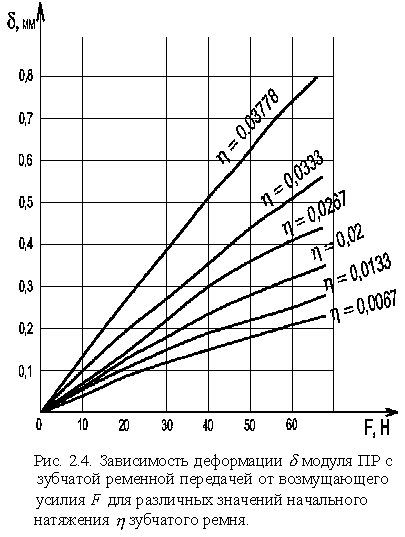
2.4 Исследование быстроходности манипулятора
Быстроходность манипулятора характеризуется временем перемещения рабочего органа в требуемую точку. Теоретические предпосылки указывают, что непосредственное влияние на величину этого времени оказывают совместные механические характеристики (СМХ) электроприводов манипулятора.
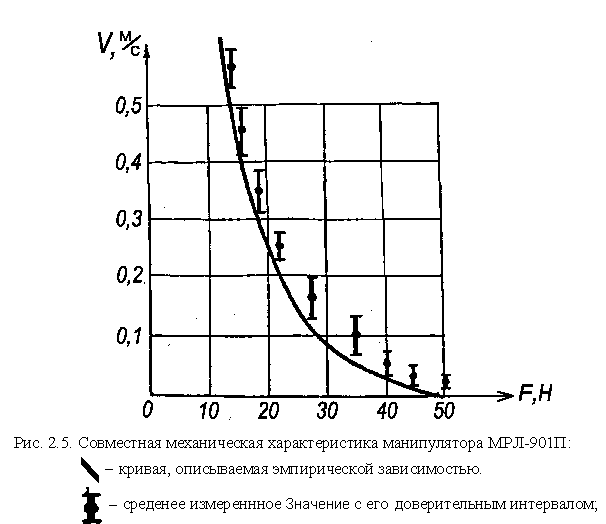
Иcследование СМХ осуществлялось путем анализа тахограмм движения манипулятора МРЛ-901П, зарегистрированных самописцем Н338Д/1. Статистически обработанные результаты экспериментов сведены в таблицу 2.6 и представлены в графическом виде на рис. 2.5.
Анализ экспирементальных данных показывает, что связь силы тяги, а, следовательно, и допустимого ускорения ![]() со значением достигнутой скорости
со значением достигнутой скорости ![]() существенно нелинейна. Для определения квазиоптимальных режимов движения манипулятора необходимо связать параметры a и V аналитическим выражением.
существенно нелинейна. Для определения квазиоптимальных режимов движения манипулятора необходимо связать параметры a и V аналитическим выражением.
Представим каждое значение ![]() СМХ в виде разности
СМХ в виде разности ![]() , где
, где ![]() -
статическая тяговая синхронизирующая сила, а
-
статическая тяговая синхронизирующая сила, а ![]() -
потери тяговой силы, зависящие от скорости движения манипулятора.
-
потери тяговой силы, зависящие от скорости движения манипулятора.
Такая запись СМХ имеет то очевидное приемущество, что для каждого конкретного образца манипулятора указанной модели могут быть введены уточнения формулы путем измерения одного лишь значения ![]() .
.
Следовательно, определение эмпирической формулы CМХ сводится к отысканию зависимости ![]() . Воспользовавшись способом отыскания эмпирических формул, приведенным в [7], легко установить, что экспериментальные точки
. Воспользовавшись способом отыскания эмпирических формул, приведенным в [7], легко установить, что экспериментальные точки ![]() наиболее точно отображают линейную зависиюсть на полулогарифмической функцональной координатной сетке. Из этого следует, что выражение
наиболее точно отображают линейную зависиюсть на полулогарифмической функцональной координатной сетке. Из этого следует, что выражение ![]() может быть описано логарифмической функцией. Из
может быть описано логарифмической функцией. Из
Результаты исследований совместной механической характеристики манипулятора МРЛ-901П.
|
Таблица 2.6 |
||||
|
Масса |
Число |
Численное значение синхронной скорости, м/c |
||
|
груза |
паралельных опытов |
среднее арифметическое |
среднее квадратическое откланение |
принимаемое значение |
|
2 |
10 |
0,80 |
0,013 |
0,8± 0,04 |
|
3 |
10 |
0,74 |
0,017 |
0,74± 0,05 |
|
4 |
10 |
0,67 |
0,016 |
0,67± 0,05 |
|
5 |
10 |
0,59 |
0,007 |
0,59± 0,02 |
|
6 |
10 |
0,49 |
0,013 |
0,49± 0,04 |
|
7 |
10 |
0,38 |
0,012 |
0,38± 0,04 |
|
8 |
10 |
0,29 |
0,010 |
0,29± 0,03 |
|
9 |
10 |
0,24 |
0,013 |
0,24± 0,04 |
|
10 |
10 |
0,20 |
0,011 |
0,20± 0,03 |
|
11 |
10 |
0,16 |
0,013 |
0,16± 0,04 |
|
12 |
10 |
0,12 |
0,006 |
0,12± 0,02 |
|
13 |
10 |
0,05 |
0,003 |
0,05± 0,01 |
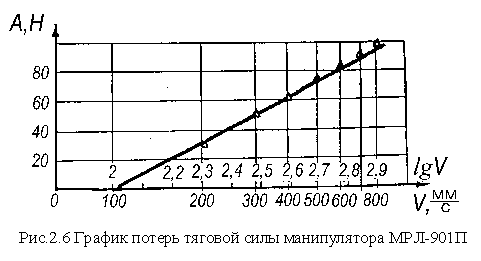
линейной зависимости, представленной на рис. 2.6 легко отыскать коэффициенты ее уравнения, вид которого ![]() . В итоге имеем:
. В итоге имеем:
|
|
(2.35) |
где: V измеряется в ![]() .
.
Следует, однако, заметить, что при нарастании значения экспериментальные точки ![]() несколько удаляются от прямой, описанной уравнением (2.35). Поэтому, с целью уточнения зависимости была внесена поправка, с учетом которой эмпирическая формула СМХ примет вид:
несколько удаляются от прямой, описанной уравнением (2.35). Поэтому, с целью уточнения зависимости была внесена поправка, с учетом которой эмпирическая формула СМХ примет вид:
|
|
(2.36) |
где: V -
измеряется в ![]() ; а
; а ![]() -
в [Н], или
-
в [Н], или
|
|
(2.37) |
где: ![]() ,
,![]() -
допустимые мгновенные значения ускорения и скорости соответственно (при этом лежит в интервале от 0,1
-
допустимые мгновенные значения ускорения и скорости соответственно (при этом лежит в интервале от 0,1![]() до 0,8
до 0,8 ![]() ).
).
2.5 Методика проведения эксперимента по определению механических характеристик манипулятора МРЛ-901П
Для исследования СМХ манипулятора портального типа МРЛ-901П наиболее удобной является следующая методика измерений.
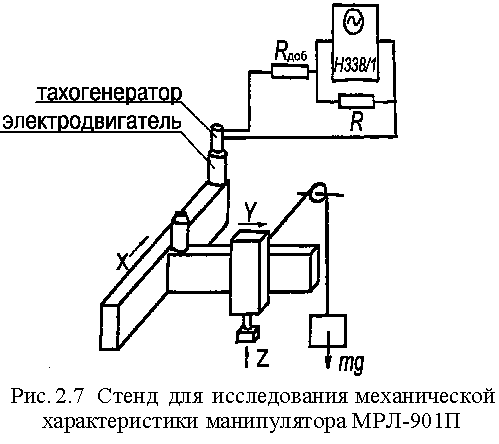
На свободный конец вала электродвигателя ШД 5Д1МУ3 крепился тахогенератор, электрический выход которого связан с измерительной схемой (рис. 2.7) вольтметра. Схема тарировалась путем задания устройством управления 2Р22 постоянных значений скорости движения рабочего органа манипулятора. При этом электродвигатель был полностью разгружен от момента нагрузки.
После тарировки к рабочему органу манипулятора прикреплялась перекинутая через ролик гибкая стальная нить, на свободный конец которой подвешивался переменный груз ![]() . По команде системы управления электродвигатель начинал равноускоренно вращаться, перемещая при этом рабочий орган манипулятора и преодолевая противодействие груза
. По команде системы управления электродвигатель начинал равноускоренно вращаться, перемещая при этом рабочий орган манипулятора и преодолевая противодействие груза ![]() . Дойдя до определенного значения скорости
. Дойдя до определенного значения скорости ![]() двигатель выходил из синхронизма, что отмечалось на фиксируемой самописцем тахограмме резким падением уровня сигнала.
двигатель выходил из синхронизма, что отмечалось на фиксируемой самописцем тахограмме резким падением уровня сигнала.
Изменение массы ![]() груза приводило к выходу электродвигателя из синхронизма уже при другом значении достигнутой скорости
груза приводило к выходу электродвигателя из синхронизма уже при другом значении достигнутой скорости ![]() . Таким образом, были найдены соотношения веса противодействующего груза и критической синхронной скорости ШД во всем диапазоне его работы.
. Таким образом, были найдены соотношения веса противодействующего груза и критической синхронной скорости ШД во всем диапазоне его работы.
Для уменьшения влияния инерционности системы задавалось ![]() , что позволило с точностью 5 -
7% полагать, что вся сила
, что позволило с точностью 5 -
7% полагать, что вся сила ![]() в момент выхода ШД из синхронизма расходуется на удержание груза
в момент выхода ШД из синхронизма расходуется на удержание груза ![]() , т. е.
, т. е. ![]() .
.
СМХ манипулятора определялась последовательно, для каждой программируемой координаты.
Для исследования других динамических характеристик, определяющих производительность манипулятора, необходимо вернуться к рассмотренному выше переходному процессу при позиционировании манипулятора.
В уравнение движения манипулятора (см. раздел 2.1) в качестве постоянных величин входят коэффициенты, пропорциональные скорости перемещения рабочего органа - коэффициенты демпфирования.
Коэффициент демпфирования b может быть определен по осциллограмме затухания колебаний рабочего органа манипулятора с использованием расчетной формулы:
|
|
(2.38) |
где m - масса подвижной части манипулятора;
u - логарифмический декремент затухания колебательного движения;
Т - период колебаний.
2.6 Сравнение результатов расчета модели с экспериментальными данными
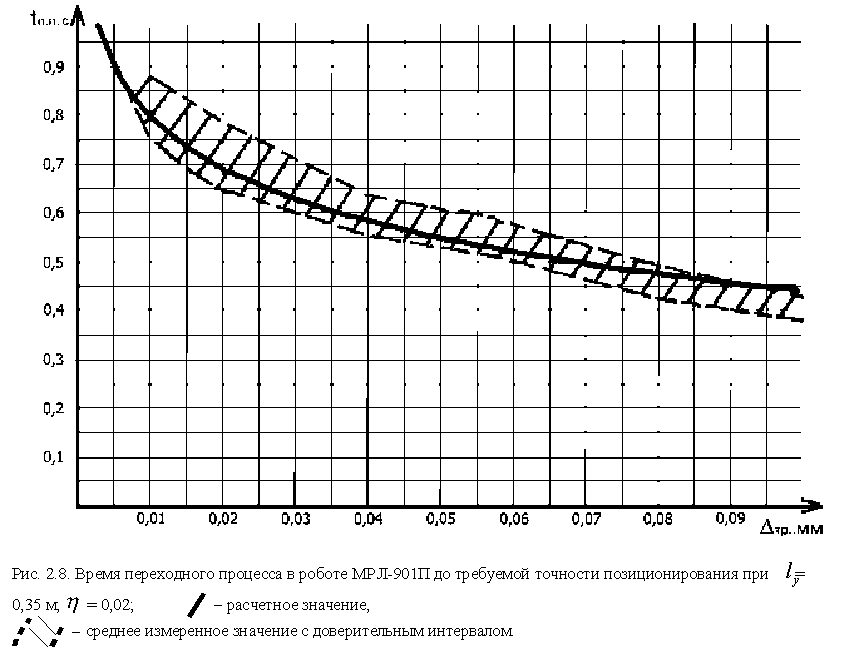
Результаты исследования жесткости и демпфирующих свойств манипулятора использовались для расчета времени переходного процесса при позиционировании. Расчет производился из аналитических выражений, полученных в разделе 2. 1 настоящей работы; его результаты сравнивались с экспериментальными данными (рис. 2.8).
Из графика видно, что расчетная кривая лежит в области экспериментально измеренных значений, это свидетельствует о достаточной точности модели, что позволяет использовать ее на практике.
3. Оптимизация скорости перемещения рабочего органа манипулятора
3.1 Время перемещения рабочего органа манипулятора
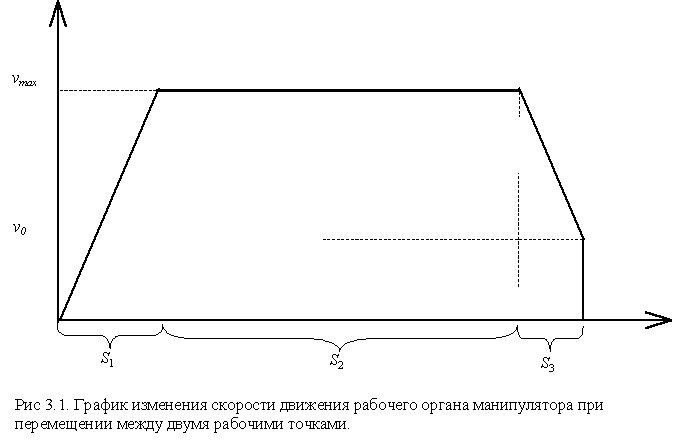
Траектория движения рабочего органа манипулятора состоит из участков разгона и торможения, а также участка, где перемещение происходит с постоянной скоростью. Очевидно, что минимальное время перемещения будет достигнуто при максимально возможных значениях скорости и ускорения, определяемых из совместной механической характеристики манипулятора (см. раздел 2.4). Заметим также, что время перемещения зависит от скорости в момент выхода на конечную точку ![]() (см. рис. 3.1). При увеличении этой скорости, протяженность участка
(см. рис. 3.1). При увеличении этой скорости, протяженность участка ![]() уменьшается, а протяженность участка
уменьшается, а протяженность участка ![]() увеличивается, тем самым возрастает средняя скорость движения рабочего органа, но при этом увеличивается время переходного процесса в момент останова. Таким образом для достижения минимального времени перемещения с учетом переходного процесса необходимо определить оптимальное значение скорости выхода на конечную точку
увеличивается, тем самым возрастает средняя скорость движения рабочего органа, но при этом увеличивается время переходного процесса в момент останова. Таким образом для достижения минимального времени перемещения с учетом переходного процесса необходимо определить оптимальное значение скорости выхода на конечную точку ![]() .
.
Время перемещения зависит от максимальных значений скорости и ускорения рабочего органа, а также от скорости в момент выхода на конечную точку рабочего органа манипулятора и складывается из следующих значений:
|
|
(3.1) |
где ![]() – время перемещения рабочего органа;
– время перемещения рабочего органа; ![]()
![]()
![]() – время перемещения рабочего органа на первом, втором и третьем участке траектории соответственно (см. рис 3.1);
– время перемещения рабочего органа на первом, втором и третьем участке траектории соответственно (см. рис 3.1); ![]() – время переходного процесса.
– время переходного процесса.
Время перемещения на первом участке траектории определяется из значений максимальной скорости и ускорения:
|
|
(3.2) |
где ![]() – максимальная скорость перемещения рабочего органа манипулятора;
– максимальная скорость перемещения рабочего органа манипулятора; ![]() – максимальное ускорение рабочего органа манипулятора.
– максимальное ускорение рабочего органа манипулятора.
На втором участке траектории рабочий орган перемещается равномерно с максимальной скоростью, при этом время перемещения составит:
|
|
(3.3) |
где S – расстояние между двумя конечными точками:![]() ;
;
Время перемещения на третьем участке траектории:
|
|
(3.4) |
где ![]() – скорость рабочего органа манипулятора в момент выхода на конечную точку.
– скорость рабочего органа манипулятора в момент выхода на конечную точку.
Длина первого участка определяется скоростью ![]() , которая достигается в конце этого участка, ускорением
, которая достигается в конце этого участка, ускорением ![]() , и выражается как:
, и выражается как:
|
|
(3.6) |
Длина третьего участка определяется начальной скоростью этого участка – ![]() , ускорением
, ускорением ![]() и конечной скоростью
и конечной скоростью ![]() :
:
|
|
(3.8) |
Для определения времени перемещения на втором участке подставим (3.6) и (3.8) в (3.3):
|
|
(3.9) |
Общее время перемещения с учетом переходного процесса получим подставляя (3.2), (3.4), (3.9) и (2.33) в (3.1):
|
|
(3.10) |
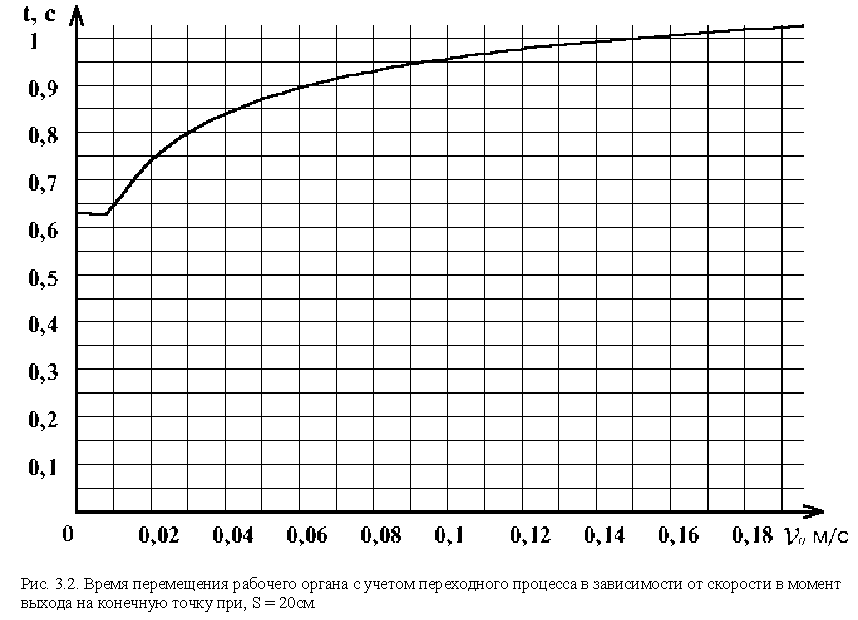
Анализируя выражение (3.10) относительно скорости выхода на конечную точку ![]() , получаем график времени перемещения рабочего органа манипулятора с учетом переходного процесса (см. рис.3.2). Из графика видно, что переходный процесс значительно влияет на время перемещения рабочего органа манипулятора.
, получаем график времени перемещения рабочего органа манипулятора с учетом переходного процесса (см. рис.3.2). Из графика видно, что переходный процесс значительно влияет на время перемещения рабочего органа манипулятора.
3.2 Время перемещения рабочего органа манипулятора при малых расстояниях между рабочими точками
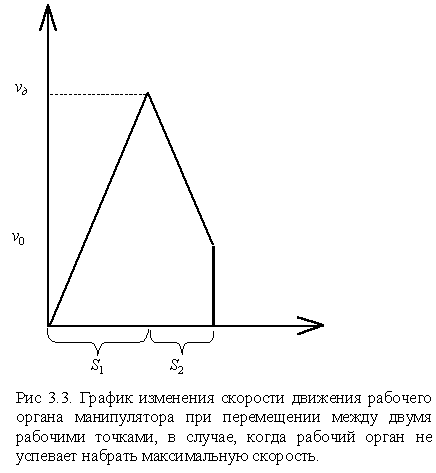
Часто возникают случаи, когда расстояние между двумя рабочими точками мало и рабочий орган манипулятора не успевает набрать максимально возможную скорость. При этом траектория движения состоит только из двух участков – разгона и торможения (см. рис. 3.3.). Скорость рабочего органа на участке разгона достигает некоторого значения ![]() , длина этого участка составит:
, длина этого участка составит:
|
|
(3.11) |
где ![]() – максимальная скорость которую успевает набрать рабочий орган манипулятора;
– максимальная скорость которую успевает набрать рабочий орган манипулятора; ![]() – максимальное ускорение рабочего органа манипулятора.
– максимальное ускорение рабочего органа манипулятора.
На втором участке траектории необходимо производить торможение рабочего органа в связи с тем что по достижению конечной точки его скорость должна иметь значение ![]() , при этом длина второго участка составит:
, при этом длина второго участка составит:
|
|
(3.12) |
тогда складывая выражения (3.11) и (3.12) получим суммарное перемещение рабочего органа:
|
|
(3.13) |
Зная расстояние между двумя рабочими точками, из (3.13) получим выражение для определения максимально достигнутой скорости:
|
|
(3.14) |
Используя (3.14) определим время перемещения рабочего органа на первом:
|
|
(3.15) |
и втором участке:
|
|
(3.16) |
Суммируя выражения (3.15), (3.16) и (2.33) получим выражение для определения времени перемещения с учетом переходного процесса при условии, что рабочий орган не успевает набрать максимальную скорость:
|
|
(3.17) |
Анализируя выражение (3.17) относительно скорости выхода на конечную точку ![]() , получаем график времени перемещения рабочего органа манипулятора с учетом переходного процесса (см. рис.3.4) для малых перемещений рабочего органа.
, получаем график времени перемещения рабочего органа манипулятора с учетом переходного процесса (см. рис.3.4) для малых перемещений рабочего органа.
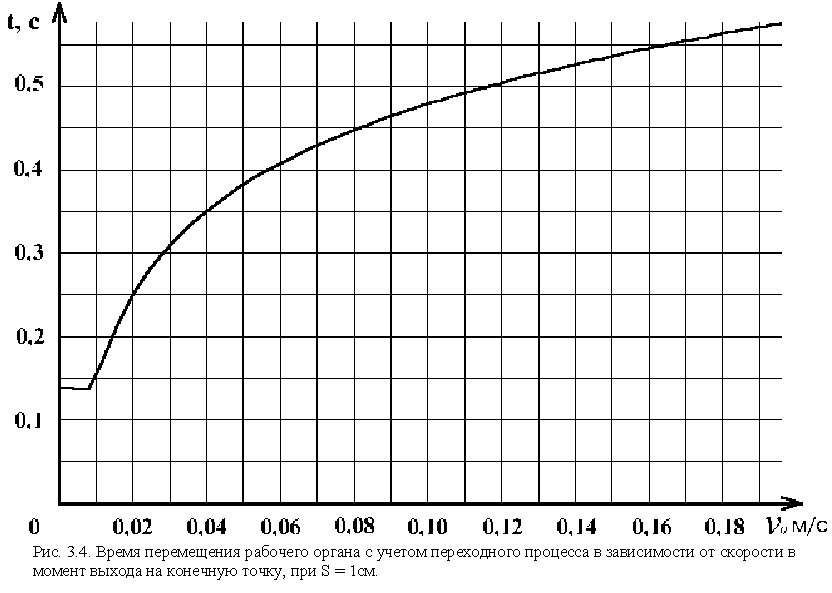
3.3 Получение оптимальной скорости в момент выхода на конечную точку
Анализ выражений (3.10) и (3.17) показывает (см. рис. 3.2, 3.4), что время перемещения рабочего органа будет минимально при таком значении скорости ![]() , когда переходный процесс в системе отсутствуют, то есть максимальная амплитуда колебаний не превышает допустимой погрешности позиционирования
, когда переходный процесс в системе отсутствуют, то есть максимальная амплитуда колебаний не превышает допустимой погрешности позиционирования ![]() . Для определения скорости
. Для определения скорости ![]() , достаточно прировнять к нулю выражение (2.33):
, достаточно прировнять к нулю выражение (2.33):
|
|
(3.18) |
Решение (3.18) относительно ![]() имеет вид:
имеет вид:
|
|
(3.19) |
Выражение (3.19) определяет такое значение скорости в момент выхода на конечную точку при которой амплитуда переходного процесса не превышает предельно допустимого значения, а следовательно время перемещения рабочего органа определяемое выражениями (3.10) и (3.17) минимально.
Анализ графиков зависимости времени перемещения с учетом переходного процесса от скорости выхода на конечную точку (см. рис. 3.2, 3.4.) показывает, что скорость выхода значительно влияет на время перемещения рабочего органа и отклонение скорости в большую сторону от расчетного значения ведет к значительным потерям времени за счет увеличения длительности переходного процесса.
Если проанализировать выражения (3.10) и (3.17) относительно допустимой погрешности позиционирования ![]() , то можно сделать вывод, что при увеличении допустимой погрешности позиционирования (см. рис. 3.5, 3.6.) наблюдается уменьшение времени перемещения, что можно использовать на операциях с низким требованием к точности, хотя это уменьшение весьма не значительное.
, то можно сделать вывод, что при увеличении допустимой погрешности позиционирования (см. рис. 3.5, 3.6.) наблюдается уменьшение времени перемещения, что можно использовать на операциях с низким требованием к точности, хотя это уменьшение весьма не значительное.
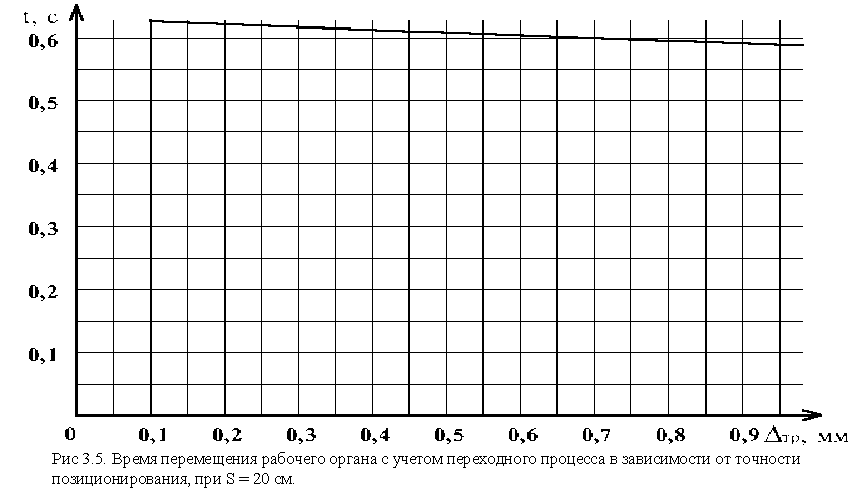
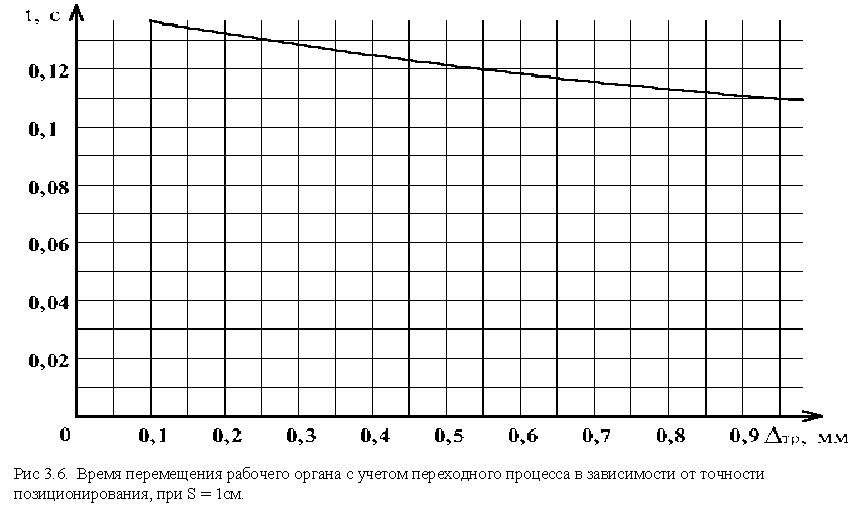
4. Программные средства для исследования динамической модели портального манипулятора
4.1 Программа для вычисления параметров переходного процесса портального манипулятора
Для исследования полученной динамической модели, построения графиков приведенных в работе, использовалась программа “Модель портального манипулятора МРЛ-901П в момент позиционирования” (см. рис. 4.1). Программа разработана для среды WIN32 API на языке C++ с использованием компилятора Borland C++ 5.02 и может выполняться на операционных системах Windows 95/98 и Windows NT.
Вычисление параметров переходного процесса в программе осуществляется с использованием выражения (2.31) при помощи которого вычисляется амплитуда колебаний рабочего органа манипулятора. По полученным значениям строится график переходного процесса и график зависимости времени переходного процесса от точности позиционирования.
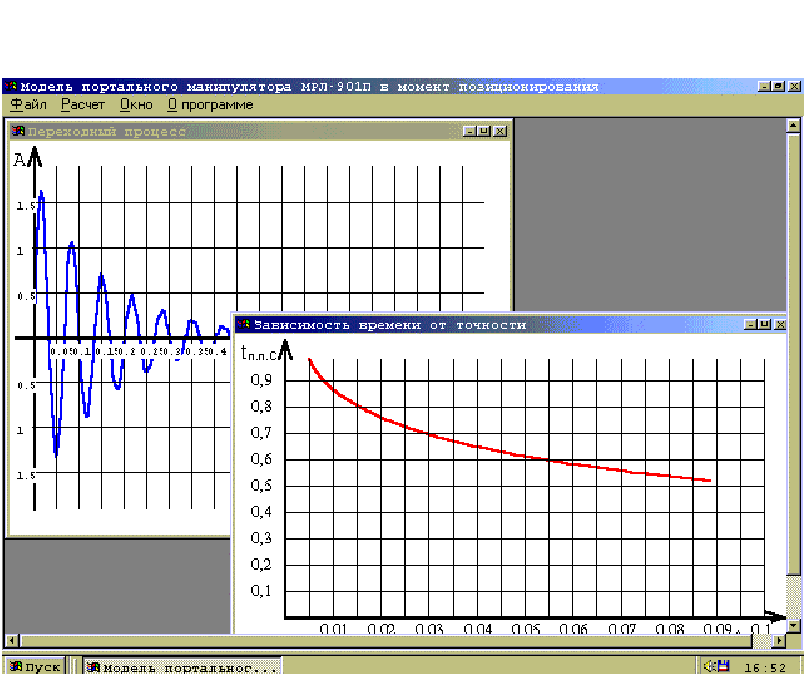
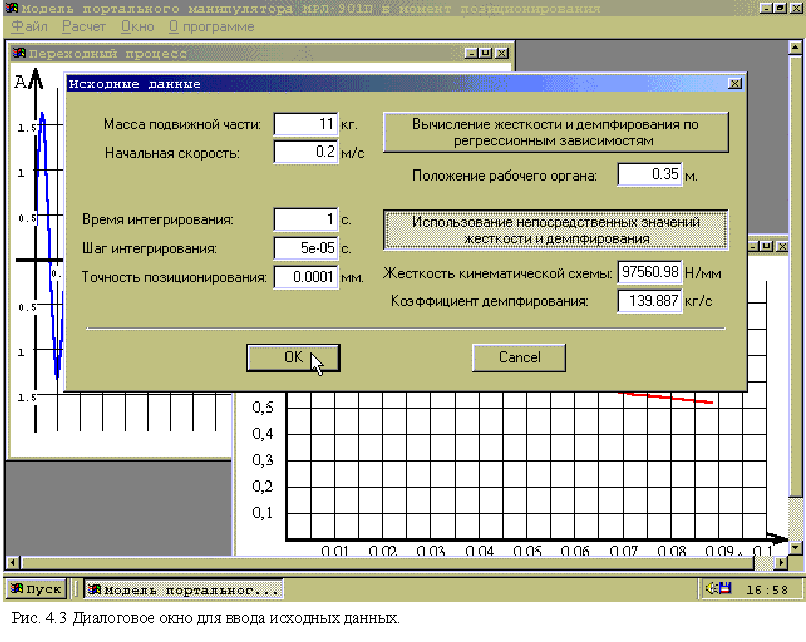
Ввод исходных данных осуществляется при помощи диалогового окна “Исходные данные” при выборе пункта меню “Расчет/Переходный процесс” (см. рис. 4.2). В диалоговое окно (см. рис. 4.3) вводятся необходимые исходные данные. После ввода исходных данных программа вычисляет амплитуду и длительность переходного процесса и выводит результаты расчетов в виде графиков.
4.2 Программа для вычисления времени переходного процесса и оптимальной скорости
Для практического использования динамической модели при разработке технологических процессов, вычисления главных параметров – времени переходного процесса и оптимальной скорости позиционирования, используются выражения (2.33) и (3.19), которые были использованы при создании программы “Mrl” (см. рис. 4.4).
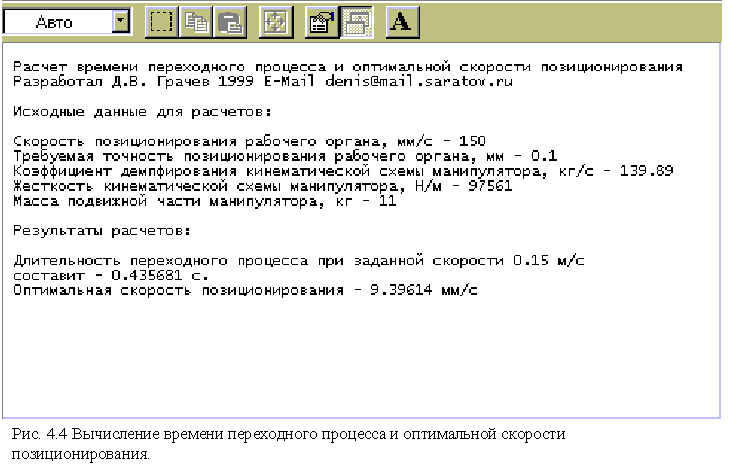
Программа “Mrl” использует текстовую консоль для ввода и вывода данных. Исходные данные и результаты вычислений записываются в файл. При необходимости, для задания имени файла результатов вычислений, можно использовать параметры командной строки.
Программа написана на языке С++ с использованием стандартных функций и может быть откомпилирована для работы в операционных системах Dos, WIN32 и UNIX. Текст программы приведен в приложении к данной работе.
Заключение
В ходе выполнения дипломной работы была построена динамическая модель портального манипулятора, параметры которой хорошо соответствуют параметрам реального манипулятора. При исследовании модели особое внимание уделялось получению выражений для определения оптимальных значений скорости движения рабочего органа с целью увеличения быстродействия манипулятора. Также в ходе исследования определены численные значения коэффициентов, входящих в динамическую модель манипулятора при его позиционировании. Установлено хорошее соответствие (ошибка в пределах 1...2%) расчетного значения продолжительности переходного процесса при позиционировании и реального позиционирования манипулятора. Разработаны методы влияния на вид и продолжительность переходного процесса путем управляемого регулирования технологических факторов: натяжения зубчатого ремня и взаимного расположения подвижных частей манипулятора МРЛ-901П. Исследованы диапазоны варьирования, определены значения технологических факторов, обеспечивающие максимальную производительность роботизированного оборудования, создаваемого на базе робота МРЛ 901П.
Проведенные исследования могут быть использованы для определения рациональных динамических параметров манипуляторов, разработки технологических процессов, а также в учебном процессе при проведении лабораторных работ.
ПРИЛОЖЕНИЕ
В приложении приведены программы для расчета параметров динамической модели портального манипулятора.
// File Mrl.сpp
// Программа для расчета времени переходного процесса и оптимальной
// скорости позиционирования
#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
#include <string.h>
int Transient(double&,
double,
double,
double,
double,
double );
int OptimalSpeed(double&,
double,
double,
double,
double );
char * s_title = "n Расчет времени переходного процесса и оптимальной "
"скорости позиционированияn Разработал Д.В. Грачев 1999"
" E-Mail denis@mail.saratov.ru";
char * s_v0 = "nn Иcходные данные для расчетов:nn Скорость"
" позиционирования рабочего органа, мм/c - # ";
char * s_d = " Требуемая точность позиционирования рабочего органа, мм - # ";
char * s_b = " Коэффициент демпфирования кинематической"
" схемы манипулятора, кг/c - # ";
char * s_c = " Жесткость кинематической схемы манипулятора, Н/м - # ";
char * s_m = " Масса подвижной части манипулятора, кг - # ";
char * s_inp = "%lf";
char * s_out = "%gn";
char * s_outp = "n Результаты расчетов: nn Длительность переходного"
" процесса при заданной скорости %g м/cn составит - %g с."
"n Оптимальная скорость позиционирования - %g мм/cn";
char * fn = "resultat.txt";
char * s_badparam = "n Недопустимый параметр - %c";
void inpparam(char** p)
{
if (*p[1] != 'f'){
printf (s_badparam, *p[1]);
exit(0);
}
strcpy(fn, p[2]);
}
int main(int as, char** av)
{
double t, v0, opv0, b, c, d, m;
printf (s_title);
if (as > 1) inpparam(av);
*strstr(s_v0,"#") = 0;
*strstr(s_d,"#") = 0;
*strstr(s_b,"#") = 0;
*strstr(s_c,"#") = 0;
*strstr(s_m,"#") = 0;
printf (s_v0);
scanf (s_inp, &v0);
v0 /= 1000;
printf (s_d);
scanf (s_inp, &d);
d /= 1000;
printf (s_b);
scanf (s_inp, &b);
printf (s_c);
scanf (s_inp, &c);
printf (s_m);
scanf (s_inp, &m);
Transient(t, v0, d, b, c, m);
OptimalSpeed(opv0, d, b, c, m);
opv0 *= 1000;
printf (s_outp, v0, t, opv0);
FILE * f_res = fopen(fn, "a+");
v0 *= 1000;
fprintf (f_res,strcat(s_v0,s_out), v0);
d *= 1000;
fprintf (f_res,strcat(s_d,s_out), d);
fprintf (f_res,strcat(s_b,s_out), b);
fprintf (f_res,strcat(s_c,s_out), c);
fprintf (f_res,strcat(s_m,s_out), m);
fprintf (f_res,s_outp, v0, t, opv0);
return 0;
}
// File speed.cpp
// Вычисление оптимального значения скорости в момент позиционирования
// по исходным данным
#include <math.h>
int OptimalSpeed(double& V0, // Начальная скорость
double Delta, // Требуемое значение точности позиционирования
double betta, // Коэффициент демпфирования
double C, // Жесткость
double m) // Масса
{
double mc2 = 2*m/C;
V0 = Delta * (1/mc2) * sqrt( fabs( pow(betta/C,2
) - 2 * mc2 ) );
return 0;
}
// File transient.cpp
// Вычисление времени перходного процесса
// по исходным данным
#include <math.h>
int Transient(double& t,// Время переходного процесса
double V0, // Начальная скорость
double Delta, // Требуемое значение точности позиционирования
double betta, // Коэффициент демпфирования
double C, // Жесткость
double m) // Масса
{
double mc2 = 2*m/C;
t = (log(V0)-log(Delta)-log(sqrt( fabs(pow(betta/C,2)-2*mc2
)
)/mc2 )
)*2*m/betta;
return 0;
}
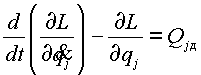 (j = 1,2,…,n),
(j = 1,2,…,n),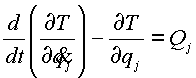 ,
,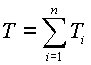 .
.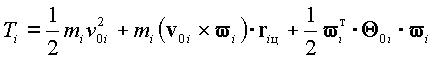 ,
,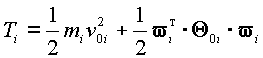 .
.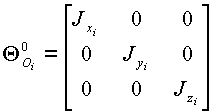 ,
,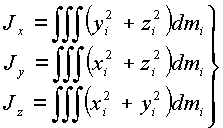 ,
,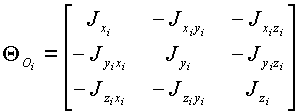 ,
,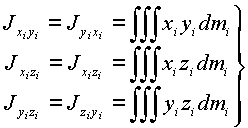
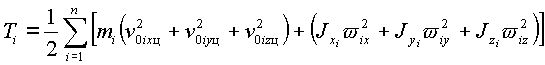 .
.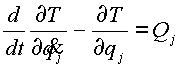 (j = 1,2,…,k),
(j = 1,2,…,k),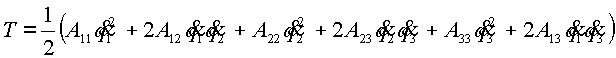 ,
,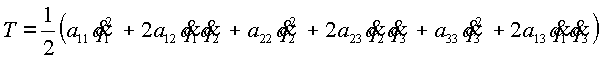
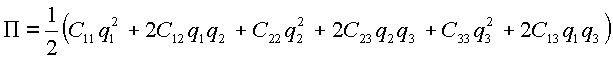
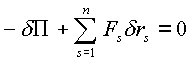 .
.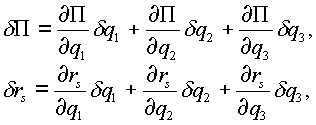
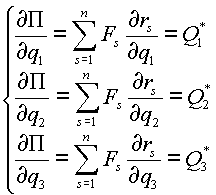 ,
,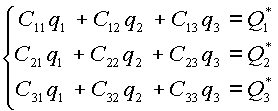 ,
,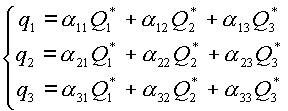 ,
,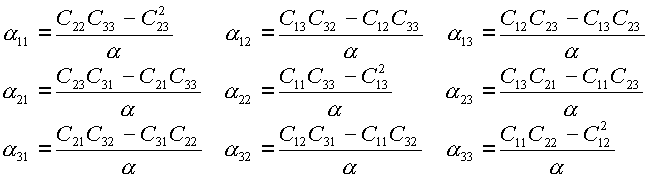
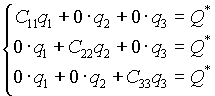 ,
,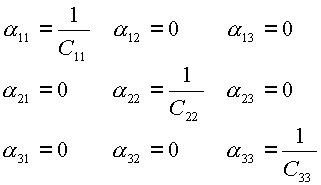
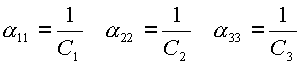 ,
,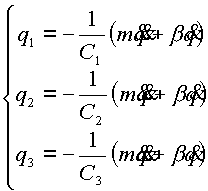
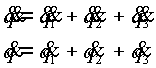 .
.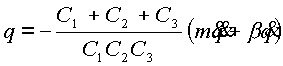
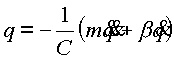 ,
,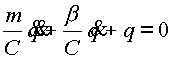 .
.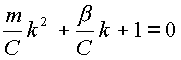 .
.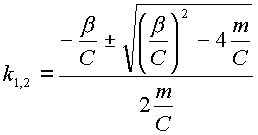
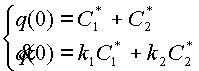 .
.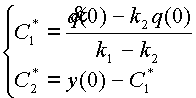 ,
,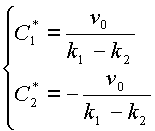
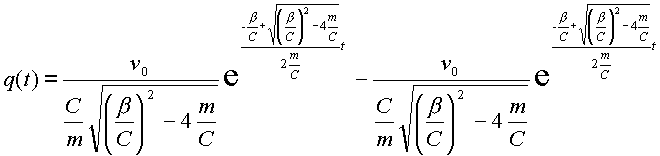
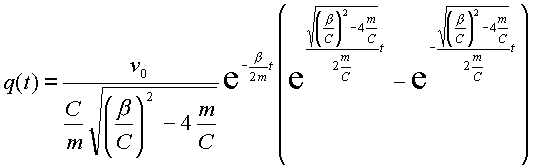 .
.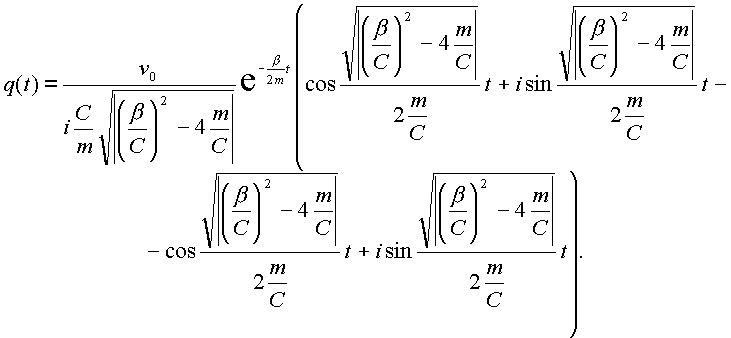
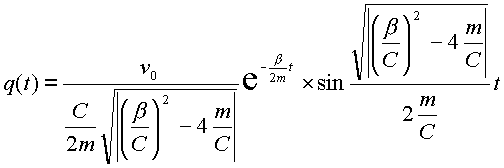
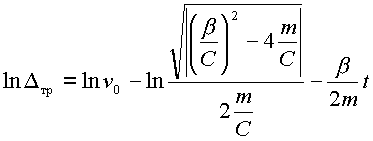 ,
,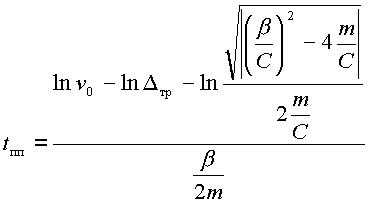
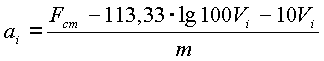 ,
,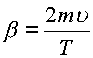 ,
,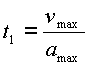 ,
,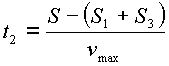 ,
,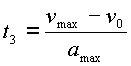 ,
,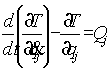 .
.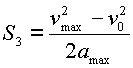 .
.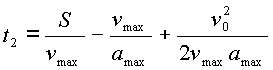 .
.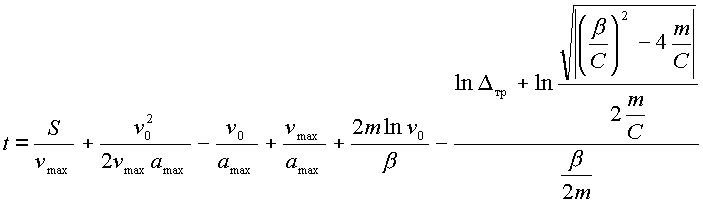 .
.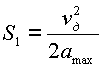 ,
,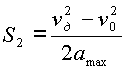 ,
,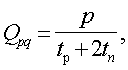 .
. .
.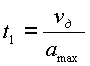 ,
,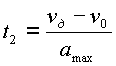 .
.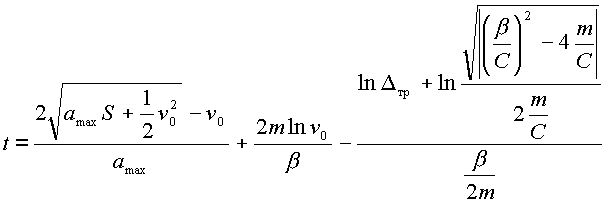
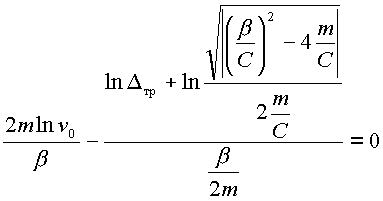 .
.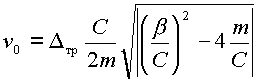 .
.