Реферат: Статистика

Часть 1.

Имеются данные о количестве заявок, поступающие на АТП по дням:

Первоначальный ряд:

5	14	7	2	8	10	2	6	12	3
5	7	9	4	3	11	12	7	8	5
12	7	11	14	3	12	8	10	8	3
13	11	8	8	2	9	8	5	14	4
10	12	6	8	2	8	7	9	2	8
4	6	13	5	3	12	2	5	7	9
5	7	2	9	5	6	14	4	7	7
10	10	5	11	8	3	2	9	10	14
10	7	4	2	8	7	14	6	8	11
13	8	12	3	11	2	7	9	9	8

Ранжированный ряд:

2	2	2	2	2	2	2	2	2	2
3	3	3	3	3	3	3	4	4	4
4	4	5	5	5	5	5	5	5	5
5	6	6	6	6	6	7	7	7	7
7	7	7	7	7	7	7	7	8	8
8	8	8	8	8	8	8	8	8	8
8	8	8	9	9	9	9	9	9	9
9	10	10	10	10	10	10	10	11	11
11	11	11	11	12	12	12	12	12	12
12	13	13	13	14	14	14	14	14	14

Величина вариации

R=xmax-xmin=14-2=12

Величина интервала:

xi	2	3	4	5	6	7	8	9	10	11	12	13	14
fi	10	7	5	9	5	12	15	8	7	6	7	3	6

Составим таблицу для накопительных частот:

xi	fi	Sfi
2¸4	22	0+22=22
4¸6	14	22+14=36
6¸8	27	36+27=63
8¸10	15	63+15=78
10¸12	13	78+13=91
12¸14	9	91+9=100

Средняя ошибка выборки:

Для дискретного ряда:

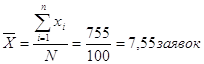
Для интервального ряда построим таблицу:

Интервалы по xi	Центр интервала	fi	xi*fi
2¸4	3	22	66
4¸6	5	14	70
6¸8	7	27	189
8¸10	9	15	135
10¸12	11	13	143
12¸14	13	9	117
		Sfi=100	Sxi*fi=720

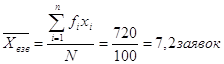
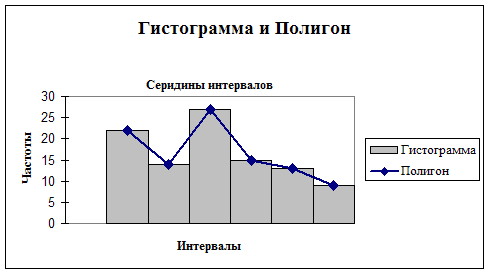
Наглядное изображение вариационного ряда

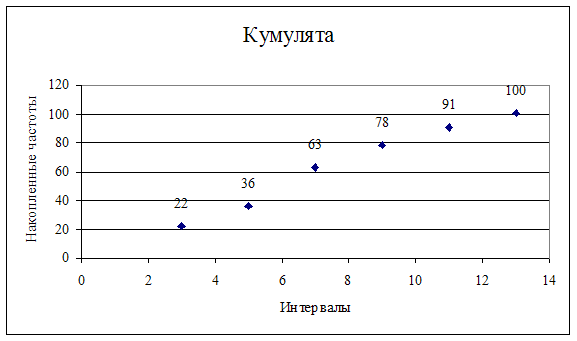
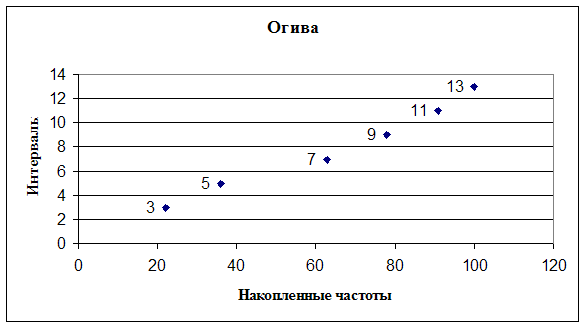
Интервалы по хi	Середина интервалов	fi	\|\|		yt	Теорет. f	Кумулятивная частота
Интервалы по хi	Середина интервалов	fi	\|\|		yt	Теорет. f	Факт.	Теорет.
2¸4	3	22	4,2	1,33	0,1647	10,3	22	10,3	11,7
4¸6	5	14	2,2	0,70	0,3123	19,5	36	29,8	6,2
6¸8	7	27	0,2	0,06	0,3982	24,9	63	54,7	8,3
8¸10	9	15	1,8	0,57	0,3391	21,2	78	75,9	2,1
10¸12	11	13	3,8	1,20	0,1942	12,1	91	88,0	3,0
12¸14	13	9	5,8	1,84	0,0734	4,6	100	92,6	7,4
									38,6

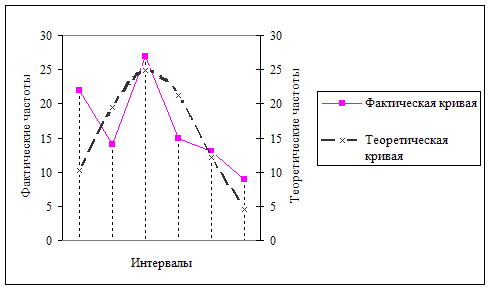l===1,17,

где l - критерий согласия;

P(l)=0,1122

С вероятностью 0,1122 можно утверждать, что отклонения фактических частот от теоретических в этом примере являются случайными. Следовательно, можно считать, что в основе фактического распределения лежит закон нормального распределения.

Среднее линейное отклонение к коэффициенту вариации:

r=,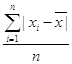

r=18/8=2,25

Относительное линейное отклонение:

nr=*100%=*100%=31%

Относительное квадратичное отклонение:

ns=*100%=*100%=42%

Мода.

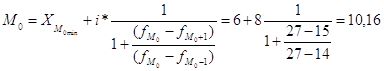
Медиана

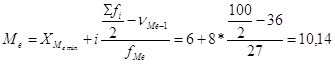
ЧастьII Анализ корреляционных зависимостей.

		Исходный ряд
№п/п	Xi	Yi	№п/п	Xi	Yi
1	20	11	26	5	6
2	8	7	27	10	5
3	5	4	28	10	6
4	10	8	29	4	4
5	10	9	30	15	9
6	15	7	31	13	4
7	10	7	32	12	8
8	10	5	33	12	4
9	5	3	34	15	4
10	10	10	35	6	3
11	10	10	36	17	3
12	5	6	37	2	3
13	11	11	38	10	4
14	4	4	39	12	5
15	10	9	40	12	6
16	7	5	41	13	6
17	8	7	42	11	4
18	25	14	43	11	4
19	11	12	44	13	12
20	4	4	45	5	4
21	8	5	46	6	4
22	7	3	47	4	4
23	4	4	48	3	1
24	20	7	49	4	4
25	5	7	50	7	3

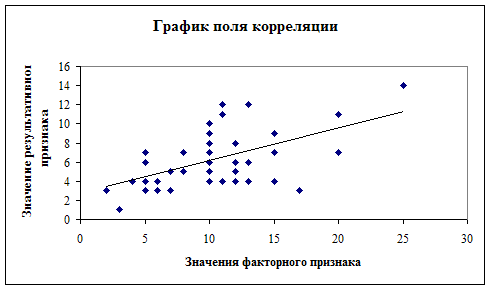
Линейная зависимость

	Ранжированный ряд
№п/п	Xi	Yi	№п/п	Xi	Yi
1	1	2	26	5	10
2	3	3	27	5	10
3	3	4	28	6	10
4	3	4	29	6	10
5	3	4	30	6	10
6	3	4	31	6	10
7	3	4	32	6	10
8	4	4	33	7	11
9	4	5	34	7	11
10	4	5	35	7	11
11	4	5	36	7	11
12	4	5	37	7	12
13	4	5	38	7	12
14	4	5	39	8	12
15	4	6	40	8	12
16	4	6	41	9	13
17	4	7	42	9	13
18	4	7	43	9	13
19	4	7	44	10	15
20	4	8	45	10	15
21	4	8	46	11	15
22	4	8	47	11	17
23	5	10	48	12	20
24	5	10	49	12	20
25	5	10	50	14	25

xi	2	3	4	5	6	7	8	10	11	12	13	15	17	20	25
fi	1	1	6	6	2	3	3	10	4	4	3	3	1	2	1

yi	1	4	5	6	7	8	9	10	11	12	14
fi	1	15	5	5	6	2	3	2	2	2	1

iy=1,86

ix=3,29

n=7
2. Построение комбинаторной таблицы

xi	2¸5,29	5,29¸8,58	8,58¸11,87	11,87¸15,16	15,16¸18,45	18,45¸21,74	21,74¸25,03
yi
1¸2,86	1
2,86¸4,72	3,3,3,3,3,3,4,4,4,4,4,4,4,	4,4,4,4,4,4,4,4
4,72¸6,58			5,5,5,5,5,6,6,6,6,6,
6,58¸8,44			7,7,7,7	7,7,8,8
8,44¸10,3				9,9,9,10,10
10,3¸12,16				11	11	12,12
12,16¸14,02							14
Число наблюдений	14	8	14	10	1	2	1

З. Нахождение теоретической формы связи.

Найдем ординату эмпирической линии регрессии

Составим вспомогательную таблицу

№ п/п	x	y	y2	x2	xy	Yt
1	2,00	3,36	11,29	4,00	6,72	2,76
2	5,29	4,00	16,00	27,98	21,16	4,66
3	8,58	5,93	35,16	73,62	50,88	6,55
4	11,87	8,80	77,44	140,90	104,46	8,44
5	15,16	11,00	121,00	229,83	166,76	10,33
6	18,45	12,00	144,00	340,40	221,40	12,23
7	21,74	14,00	196,00	472,63	304,36	14,12
S	83,09	59,09	600,89	1289,35	875,74	59,09

Уравнение прямой

ì a0*n+a1*Sx=Sy

îa0*Sx+a1*Sx2=Sx*y

a0=1,61 , а1=0,58

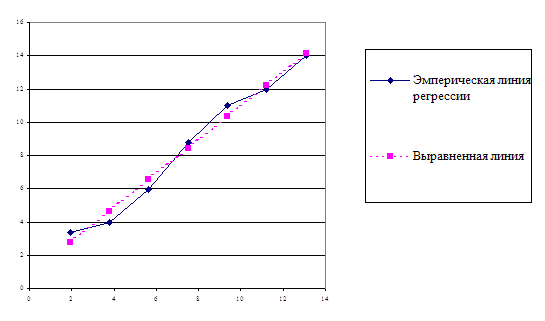
Расчет коэффициента корреляции

x	y	*(x-)*	*(y-)*	**(x-)(y-)***	*(x-)2*	*(y-)2*
2	3,36	-9,87	-5,08	50,15	97,42	25,82
5,29	4	-6,58	-4,44	29,22	43,30	19,73
8,58	5,93	-3,29	-2,51	8,26	10,82	6,31
11,87	8,8	0,00	0,36	0,00	0,00	0,13
15,16	11	3,29	2,56	8,42	10,82	6,55
18,45	12	6,58	3,56	23,42	43,30	12,66
21,74	14	9,87	5,56	54,86	97,42	30,90
			S	174,34	303,07	102,09

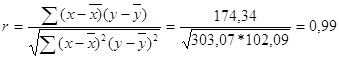
-1<0,99<+1 Þ зависимость между x и y прямая