Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Реферат: Курсовая работа по теории электрических цепей
Реферат: Курсовая работа по теории электрических цепей
Часть 1.
Анализ цепи во временной области методом переменных состояния при постоянных воздействиях.
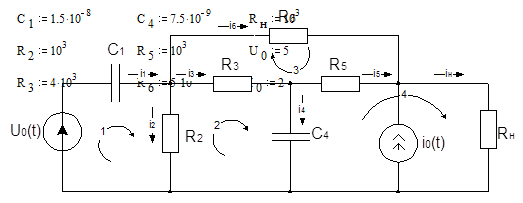 |
Дано:
Для схемы:
U0(t)= U0=const U0=5 В
i0(t)=I0d1(t) I0=2 A
1.1 Составить уравнения состояния для цепи при t³0.
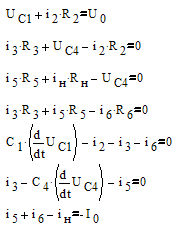 Переменными состояния для данной схемы
будут являться напряжения на емкостях С1 и С4. Для нахождения уравнений состояния запишем уравнения
по I и II законам Кирхгофа:
Переменными состояния для данной схемы
будут являться напряжения на емкостях С1 и С4. Для нахождения уравнений состояния запишем уравнения
по I и II законам Кирхгофа:
(1)
Для нахождения производных переменных состояния решим следующую систему, полученную из системы (1), приняв за неизвестные все токи, участвующие в системе (1) и первые производные переменных состояния. Переменные состояния примем за известные величины для получения их в правой части уравнений состояния:
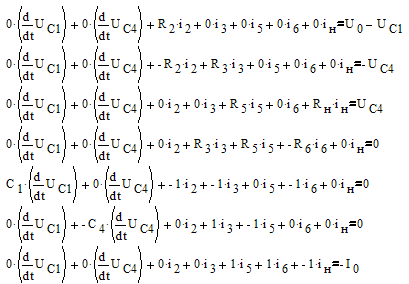
(2)
Решаем эту систему в матричном виде с помощью MathCad:

Таким образом, уравнения состояния будут иметь
вид:

1.2 Найти точные решения уравнений состояния.
Сначала найдем корни характеристического уравнения как собственные числа матрицы, составленной из коэффициентов при переменных состояния в уравнениях состояния:
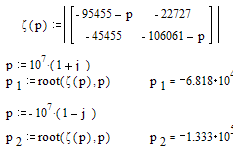
Общий вид точных решений уравнений состояния:
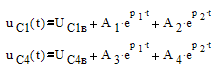
Вынужденные составляющие найдем как частное
решение уравнений состояния, учитывая то, что если в цепи включены только
постоянные источники питания, значит, и принужденные составляющие будут
константами, соответственно производные принужденных составляющих будут равны
нулю. Учитывая выше сказанное, найдем их из уравнений состояния следующим
способом:
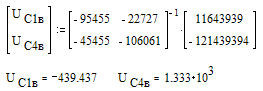
![]()
Начальные условия (находятся из схемы):
Для нахождения постоянных интегрирования A1, A2, A3, A4 требуется 4 уравнения. Первые два уравнения получим из выражений точного решения уравнений состояния, учитывая законы коммутаций: переменные состояния не меняют своего значения в момент коммутации.
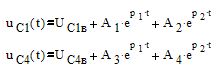
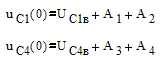
При t=0:
Далее найдем значения производных переменных состояния при t=0 из уравнений состояния:

Выражения эти производных найденные из выражений
решения уравнений состояния:
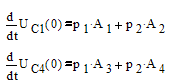
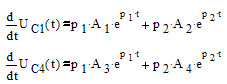
При t=0:
Таким образом имеем 4 уравнения для нахождения постоянных интегрирования, находим их:

Точные решения уравнений состояния:

1.2 Найти решения уравнений состояния, используя один из численных методов.
Для численного решения уравнений состояния воспользуемся алгоритмом Эйлера:
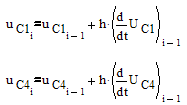
Подставляя выражения производных из уравнений
состояния:
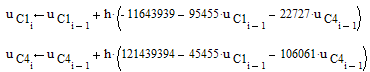
h
– шаг расчета =2*10-6 с. i=1…100. Переменными с нулевыми
индексами являются значения начальных условий.
1.2.2 Найти точные решения уравнений состояния.(второй способ)
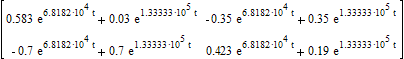
e(A)t = a0 + a1(A) e(A)t=
(X) = [e(A)t-1][A]-1[B][V]

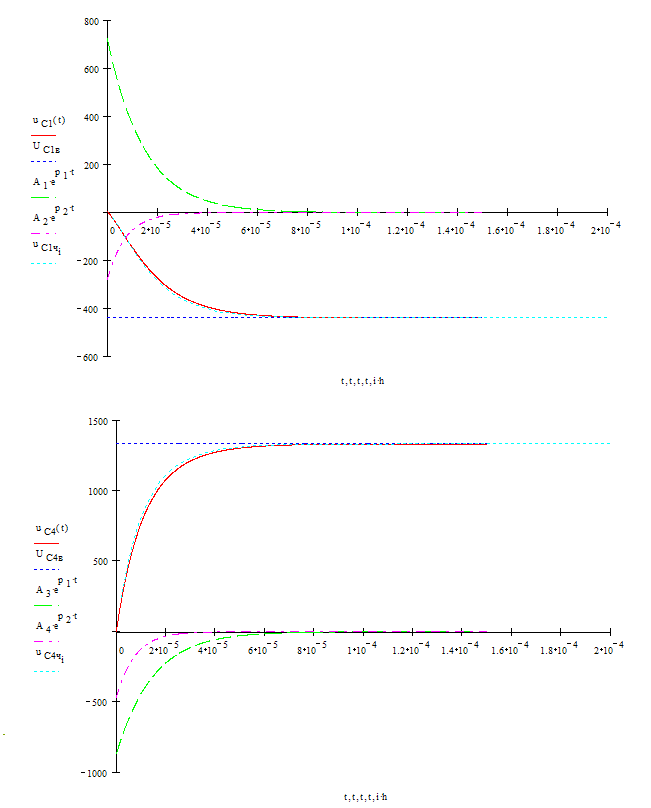
1.4 Построить точные и численные решения уравнений состояния, совместив их попарно на одном графике для каждой из переменной состояния.
Часть 2.
Анализ цепи операторным методом при апериодическом воздействии.
Анализу подлежит следующая цепь:
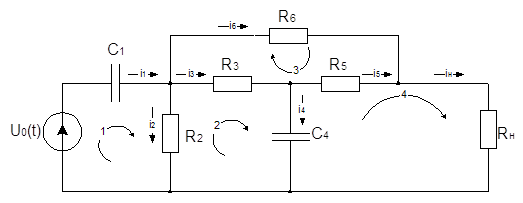
Параметры импульса: Um=10 В tu=6*10-5 c
Форма импульса:
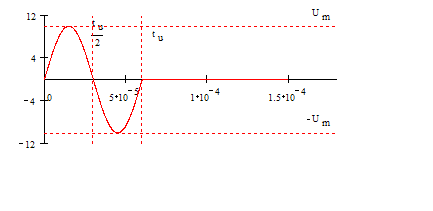
2.1 Определить функцию передачи: ![]()
воспользуемся методом пропорциональных величин и определим u(t)=1(t), его Лапласово изображение U0(s)=1/s.
Запишем уравнения по законам Кирхгофа в операторной форме, учитывая, что начальные условия нулевые:
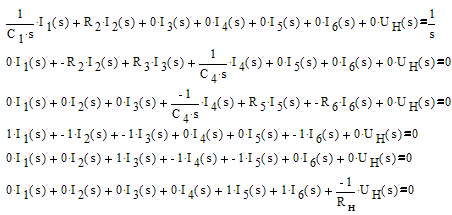
Решаем эту систему:

Таким образом:
![]()
Функция передачи:
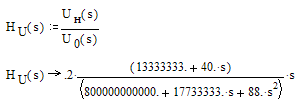
2.2 Найти нули и полюсы функции передачи и
нанести их на плоскость комплексной частоты.Полюсы:
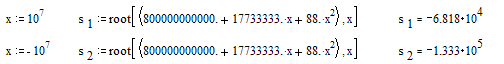
Нули:
![]()
Плоскость комплексной частоты:
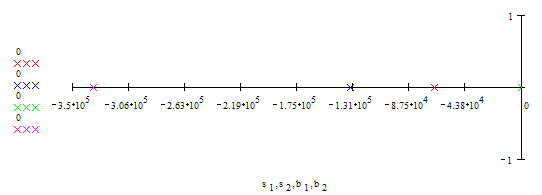
2.3 Найти переходную и импульсную
характеристики для выходного напряжения.
![]() Импульсная характеристика:
Импульсная характеристика:
Выделим постоянную часть в HU(s):
![]()
Числитель получившейся дроби:
![]()
Упрощенное выражение HU(s):
![]()
Для нахождения оригинала воспользуемся теоремой
о разложении. Для этого найдем производную знаменателя:
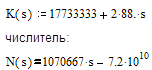
Коэффициенты разложения:
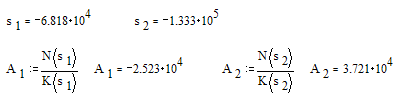
Оригинал импульсной характеристики:
![]()
![]()
Переходная характеристика:
Этим же методом находим оригинал характеристики:
![]()
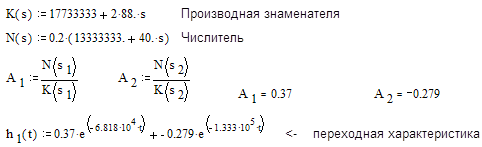
2.4 Определить изображение по Лапласу входного импульса.
Изабражение по Лапласу фукции f(t):
![]()
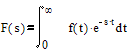 |
Входной импульс представляет собой функцию
Поэтому изображение входного сигнала будет
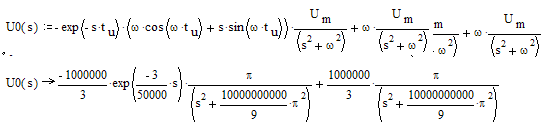
2.5 Найти напряжение на выходе схемы, используя HU(s).
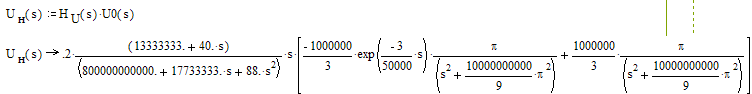
Изображение выходного сигнала:
Найдем отдельно оригиналы части выражения при ![]() и при части, не
имеющей этого множителя:
и при части, не
имеющей этого множителя:
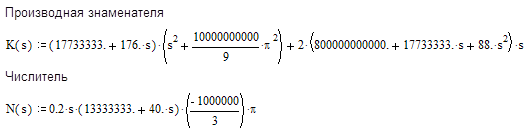 |
Для части выражения при
 |
Для части выражения не имеющей множителя
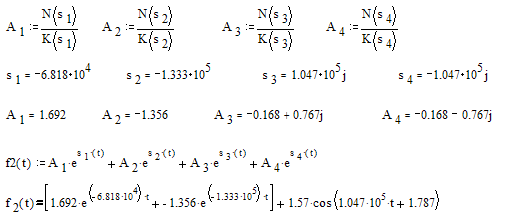
Функция напряжения на выходе схемы, получена с использованием теоремы о смещении оригинала:
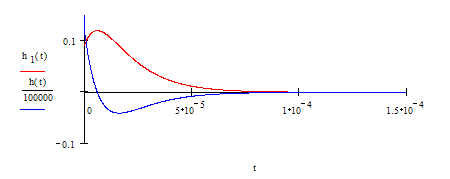
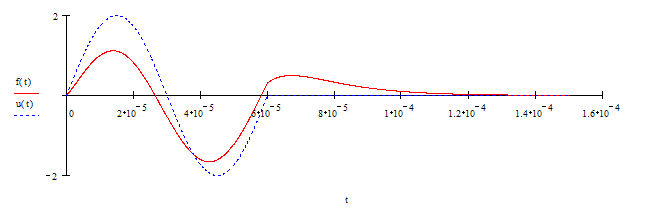
2.6 Построить на одном графике переходную и импульсную характеристики цепи, на другом – входной и выходной сигналы.
Переходная h1(t) и импульсная h(t) характеристики.
Входной и выходной сигналы.
Часть 3.
Анализ цепи частотным методом при апериодическом воздействии.
3.1 Найти и построить амплитудно-фазовую (АФХ), амлитудно-частотную (АЧХ) и фазо-частотную (ФЧХ) характеристики функций передачи HU(s).
амплитудно-фазовая характеристика:
![]()
амплитудно-частотная характеристика:
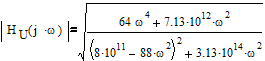
фазо-частотная характеристика:
![]()
График АЧХ:
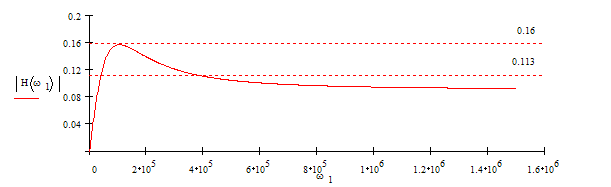
График ФЧХ:
3.2
Определить полосу пропускания цепи по уровню 0.707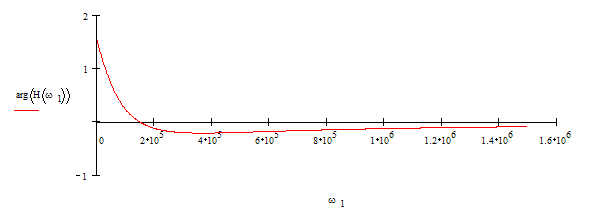
![]() .
.
Из
графика АЧХ находим полосу пропускания цепи: ![]()
![]() с-1.
с-1.
3.3
Найти и построить амплитудный и фазовый спектры входного сигнала по уровню 0.1![]() .
.
Амплитудный спектр входного сигнала:
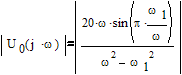
Фазовый спектр входного сигнала:
![]()
График амплитудного и фазового спектра входного
сигнала:
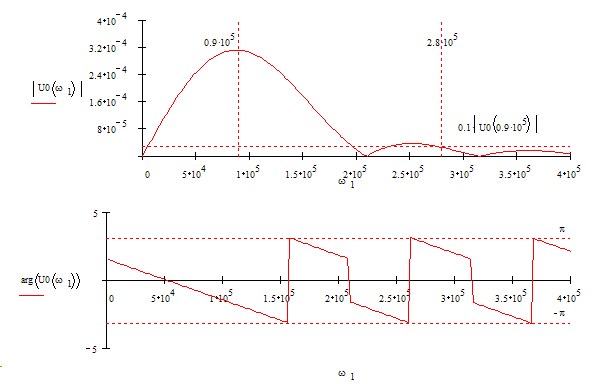 |
Ширина спектра
3.4 Сопоставляя спектры входного сигнала с частотными характеристиками цепи, дать предварительные заключения об ожидаемых искажениях сигнала на выходе цепи.
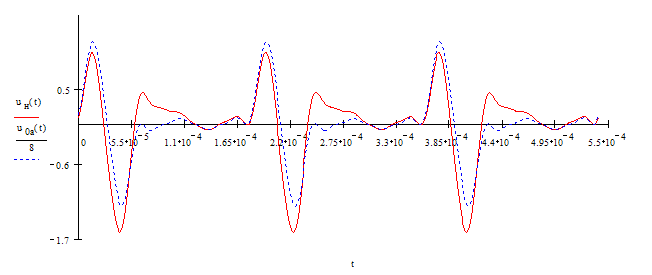
Существенная часть амплитудного спектра входного сигнала укладывается в полосу пропускания, исключая полосу 0-5*104 с-1, где и будут наблюдаться основные амплитудные искажения. Фазо-частотная характеристика цепи нелинейна, поэтому здесь будут иметь место фазовые искажения, что видно на рис.
3.5 Найти и построить амплитудный и фазовый спектр выходного сигнала.
Получаются по формулам:
![]()
![]()
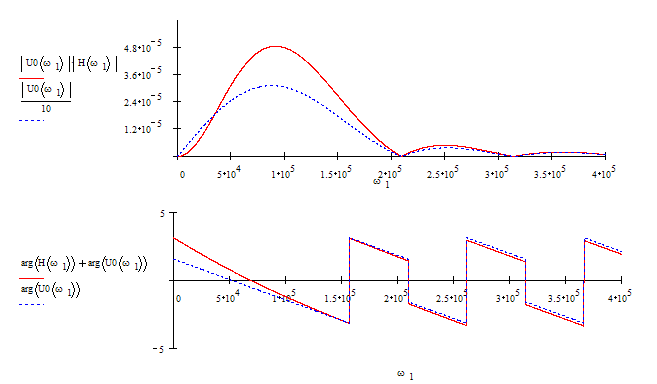
3.6 Определить выходной сигнал по вещественной частотной характеристике,
используя приближенный метод Гиллемина.
Вещественная характеристика:
![]()
Существенную часть этой характеристики кусочно-линейно аппроксимируем. Начертим первую и вторую производную кусочно-линейной аппроксимирующей функции.
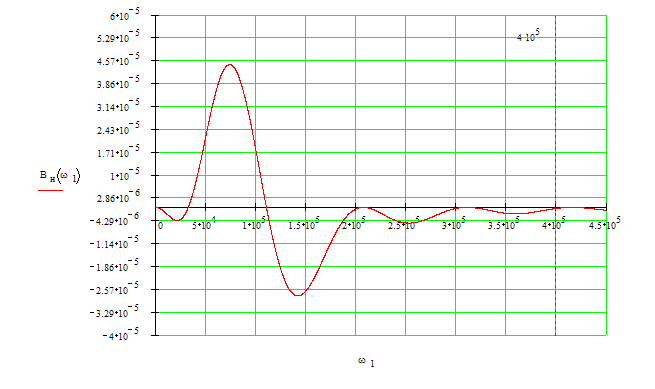
График вещественной характеристики:
![]()
Тогда: ![]()
График напряжения, вычисленного по этой формуле, и полученный в ч.2.
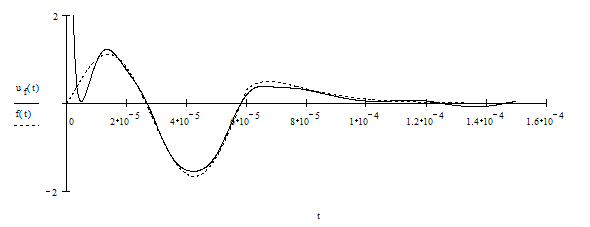
Часть 4.
Анализ цепи частотным методом при периодическом воздействии.
Дано: T=18*10-5c. Um=10 В. tu=6*10-5c.
форма сигнала u0(t):
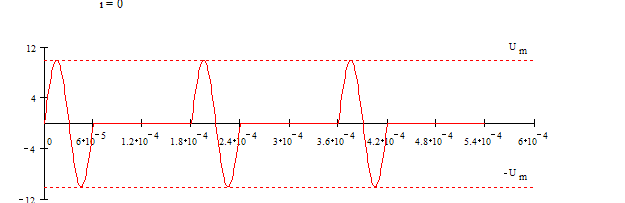
4.1 Разложить в ряд Фурье заданную периодическую последовательность
импульсов и построить ее амплитудный и фазовый спектры.
Коэффициенты ряда Фурье для u0(t) найдём из следующего соотношения:
![]()
где w1 = 2p/Т , k=0, 1, 2, ... w1=3.491*104с.
Значения Ak и ak приведены в табл. ,на рис. , построены соответственно амплитудный и фазовый спектры заданной периодически последовательности сигналов u0(t).
| k |
Ak |
ak |
| 0 | 0 | 0 |
| 1 | 2.067 | 0.524 |
| 2 | 3.308 | -0.524 |
| 3 | 2.774 | -1.571 |
| 4 | 2.363 | -2.618 |
| 5 | 1.034 | 2.618 |
| 6 | 0 | 1.571 |
| 7 | 0.413 | -2.618 |
| 8 | 0.301 | 2.618 |
| 9 | 0 | 1.571 |
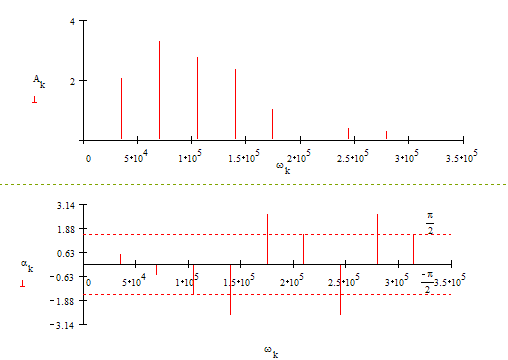
Таким образом, в соответствии с шириной спектра
.
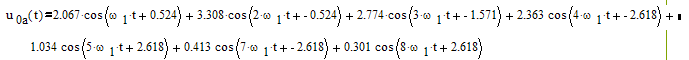
![]()
4.2 Построить на одном графике заданную периодическую последовательность импульсов и ее аппроксимацию отрезком ряда Фурье, число гармоник которого определяется шириной амплитудного спектра входного сигнала, найденной в п 3.3.
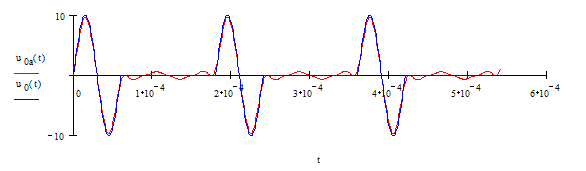
4.3 Используя рассчитанные в п. 3.1 АЧХ и ФЧХ функции передачи цепи,
определить напряжение или ток на выходе цепи в виде отрезка ряда Фурье.
Для определения коэффициентов ряда Фурье выходного напряжения вычислим значения АЧХ и ФЧХ функции передачи для значений kw1, k=0, 1, 2, ..., 8. Тогда
![]()

![]()
| k |
Ak |
ak |
| 0 | 0 | 0 |
| 1 | 0.208 | 1.47 |
| 2 | 0.487 | -0.026 |
| 3 | 0.436 | -1.355 |
| 4 | 0.361 | -2.576 |
| 5 | 0.15 | 2.554 |
| 6 | 0 | 1.443 |
| 7 | 0.054 | -2.785 |
| 8 | 0.037 | 2.429 |
| 9 | 0 | 1.371 |
В итоге получим:
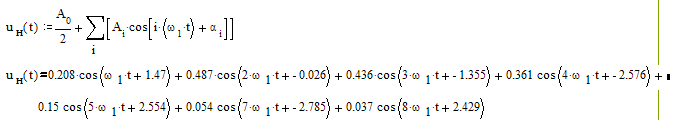
4.4 Построить напряжение на выходе цепи в виде суммы гармоник найденного отрезка ряда Фурье.