
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Реферат: Курсовая работа
Реферат: Курсовая работа
Исследование сложной электрической цепи постоянного тока методом узловых потенциалов.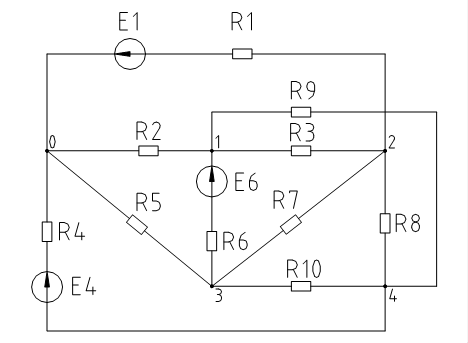
R1=130 Ом
R2=150 Ом
R3=180 Oм
R4=110 Oм
R5=220 Oм
R6=75 Oм
R7=150 Oм
R8=75 Oм
R9=180 Oм
R10=220 Oм
E1=20 В
E4=5.6 В
E6=12 В
1. Расчет узловых потенциалов.
Заземляем 0й узел, и относительно него рассчитываем потенциалы остальных узлов.
Запишем матрицу проводимостей для этой цепи:
Y=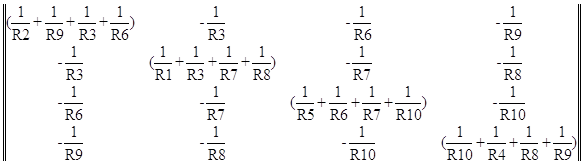
После подстановки значений:
Y=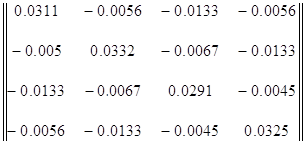
Составляем матрицу узловых токов:
I=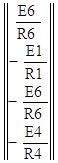
По методу узловых потенциалов мы имеем уравнение в матричном виде:
![]()
Y – матрица проводимостей;
U – матрица узловых потенциалов;
I – матрица узловых токов.
Из этого уравнения выражаем U:
![]()
Y-1 – обратная матрица;
Решаем это уравнение, используя математическую среду Matlab: U=inv(Y)*I
inv(Y) – функция ищущая обратную матрицу.
U=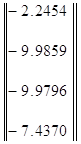
Зная узловые потенциалы, найдем токи в ветвях:
i1=![]() =
-0.0768; i2=
=
-0.0768; i2=![]() = -0.0150; i3=
= -0.0150; i3=![]() = -0.0430;
= -0.0430;
i4=![]() =
-0.0167; i5=
=
-0.0167; i5=![]() = -0.0454; i6=
= -0.0454; i6=![]() = 0.0569;
= 0.0569;
i7=![]() =
4.2281´10-5; i8=
=
4.2281´10-5; i8=![]() = 0.0340; i9=
= 0.0340; i9=![]() = -0.0288;
= -0.0288;
i10=![]() =
0.0116
=
0.0116
2. Проверка законов Кирхгофа.
Первый закон
для 0го узла : i4+i2-i5-i1=0
для 1го узла : i2+i6-i3-i9=0
для 2го узла : i3+i7-i8-i1=0
для 3го узла : i10-i7-i6-i5=0
для 4го узла : i8+i4+i9-i10=0
Второй закон
1й контур : i1R1+i2R2+i3R3=E1 Þ 20=20
2й контур : i2R2-i6R6+i5R5=-E6 Þ -12=-12
3й контур : i4R4-i8R8-i3R3-i2R2=E4 Þ 5.6=5.6
4й контур : i3R3+i8R8+i10R10+i6R6=-E6 Þ -12=-12
5й контур : i3R3-i7R7+i6R6=E6 Þ 12=12
6й контур : i9R9-i8R8-i3R3=0 Þ 0=0
3. Проверка баланса мощностей в схеме
Подсчитаем мощность потребителей:
P1=i12´R1+i22´R2+i32R3+i42´R4+i52´R5+i62´R6+i72´R7+i82´R8+i92´R9+i102´R10+E4´i4= 2.2188
Сюда включёна мощность Е4 так как он тоже потребляет энергию.
Подсчитаем мощность источников:
P2=E1´i1+E6´i6=2,2188
P1-P2=0
4. Метод эквивалентного генератора.
Рассчитаем ток в ветви с максимальной мощностью, методом эквивалентного генератора.
Сравнивая мощности ветвей видим, что максимальная мощность выделяется в первой ветви, поэтому уберём эту ветвь и для получившейся схемы рассчитаем Uxx и Rэк .
Расчёт Uxx методом узловых потенциалов:
Матрица проводимостей:
Y=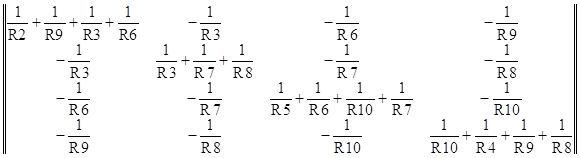
Матрица узловых токов:
I=![]()
По методу узловых потенциалов находим:
![]() =
=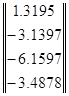
Но нас интересует только разность потенциалов между 0ым и 3им узлами: U30=Uxx =-6.1597.
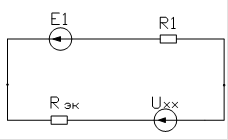
Þ
I1=![]() =
=![]() =-0.0686
=-0.0686![]()
Где эквивалентное сопротивление находится следующим образом:
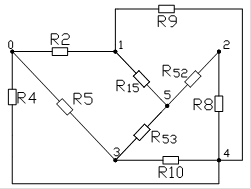
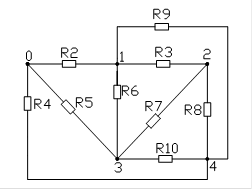
∆123 Þ :123
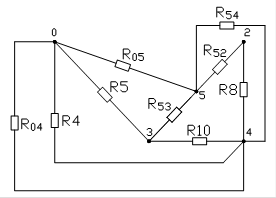
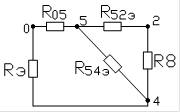
:054 Þ ∆054 :054 Þ ∆054
![]()
:024 Þ ∆024
При переходе от :
Þ ∆
используется формулы преобразования: ![]() , а при
переходе ∆ Þ ::
, а при
переходе ∆ Þ ::
![]() , две остальные формулы и в
том, и в другом случаях получаются путем круговой замены индексов.
, две остальные формулы и в
том, и в другом случаях получаются путем круговой замены индексов.
Определим значение сопротивления, при котором будет
выделяться максимальная мощность. Для этого запишем выражение мощности на этом
сопротивлении: ![]() . Найдя
производную этого выражения, и приравняв её к нулю, получим: R=Rэк, т.е. максимальная мощность выделяется при
сопротивлении нагрузки равном внутреннему сопротивлению активного
двухполюсника.
. Найдя
производную этого выражения, и приравняв её к нулю, получим: R=Rэк, т.е. максимальная мощность выделяется при
сопротивлении нагрузки равном внутреннему сопротивлению активного
двухполюсника.
5.
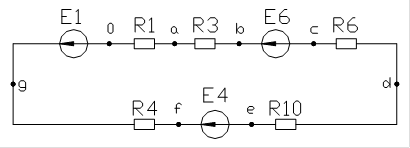 Построение потенциальной диаграммы по контуру.
Построение потенциальной диаграммы по контуру.
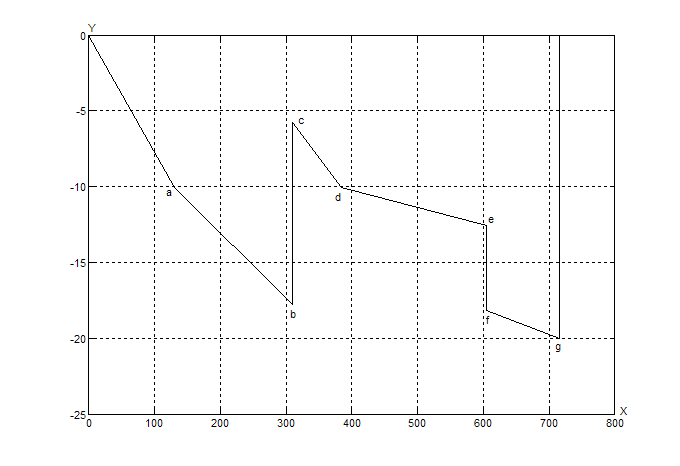 По оси X
откладывается сопротивление участка, по оси Y потенциал
соответствующей точки.
По оси X
откладывается сопротивление участка, по оси Y потенциал
соответствующей точки.
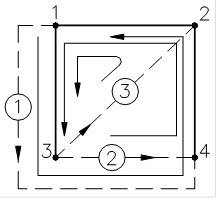
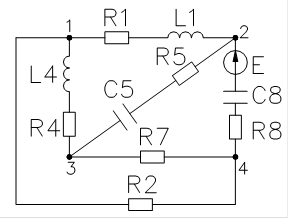
Þ
Переобозначим в соответствии с графом:
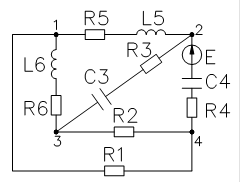
R1=110 Ом L5=50 млГ С4=0.5 мкФ
R2=200 Ом L6=30 млГ С3=0.25 мкФ
R3=150 Ом
R4=220 Ом E=15 В
R5=110 Ом w=2pf
R6=130 Ом f=900 Гц
1. Расчет токов и напряжений в схеме, методом контурных токов.
Матрица сопротивлений:
Z=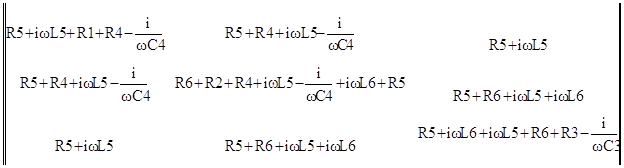 =
=
=102´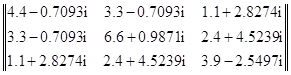
Матрица сумм ЭДС,
действующих в ком контуре: Eк=![]()
По методу контурных
токов: Ix=Z-1´Eк=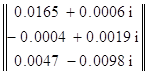
Действующие значения: Ix=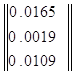
Выражаем токи в ветвях дерева: I4=I1+I2= 0.0161+0.0025i I4=0.0163
I5=I1+I2+I3=0.0208-0.0073i Þ I5=0.0220
I6=I2+I3=0.0043-0.0079i I6=0.0090
Напряжения на элементах:
UR1=I1´R1=1.8162 UL5=I5´w´L5=6.2327 UC3=I3´![]() =7.6881
=7.6881
UR2=I2´R2=0.3883 UL6=I6´w´L6=1.5259 UC4=I4´![]() =5.7624
=5.7624
UR3=I3´R3=1.6303
UR4=I4´R4=3.5844
UR5=I5´R5=2.4248
UR6=I6´R6=1.1693
2. Проверка баланса мощностей.
Активная мощность:
P=I12´R1+I22´R2+I32´R3+I42´R4+I52´R5+I62´R6=0.1708
Реактивная мощность:
Q=I52´w´L5+I62´w´L6-I32´![]() =-0.0263
=-0.0263
Полная мощность:
S=![]() =0.1728
=0.1728
С другой стороны:
Активная мощность источника:
P=E´I4´cos(arctg![]() )=0.1708
)=0.1708
Реактивная мощность источника:
Q=E´I4´sin(arctg![]() )=-0.0265
)=-0.0265
Полная мощность источника:
S=E´I4=0.1728
3. Построение векторной диаграммы и проверка 2го закона Кирхгофа.
Для 1го контура:
I1´R1+I4´R4+I4´ ![]() +I5´R5+I5´282.7433i-E=0.0088-0.0559i
+I5´R5+I5´282.7433i-E=0.0088-0.0559i
Для 2го контура:
I2´R2+I4´R4+I4´![]() +I5´282.7433i+I5´R5+I6´169.6460i+I6´R6=0.0088- 0.0559i
+I5´282.7433i+I5´R5+I6´169.6460i+I6´R6=0.0088- 0.0559i
Для 3го контура:
I5´R5+I6´169.6460i+I6´R6+I3´![]() +I3´R3+I5´282.7433i=-0.0680-0.0323i
+I3´R3+I5´282.7433i=-0.0680-0.0323i
Векторная диаграмма:
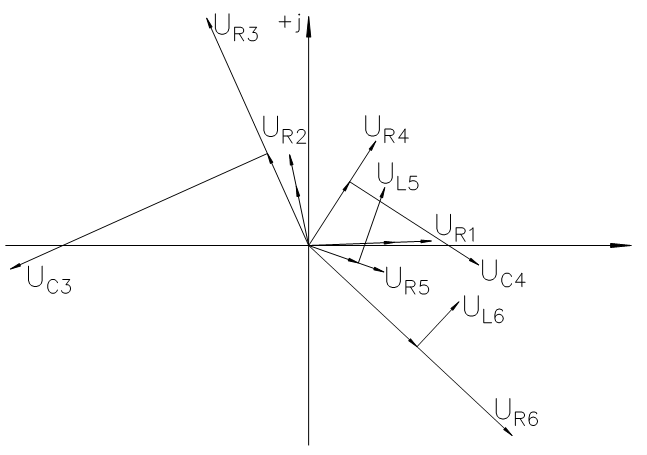
Топографическая диаграмма для 1го контура:
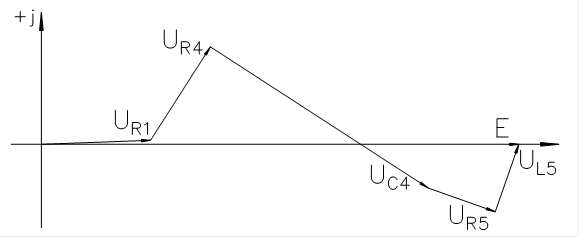
Топографическая диаграмма для 2го контура:
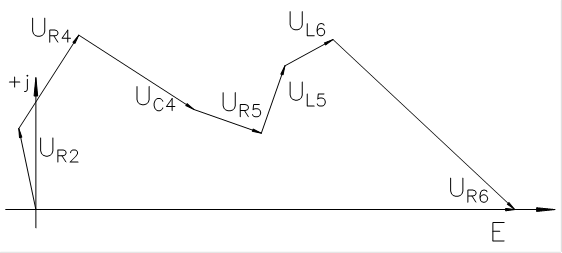
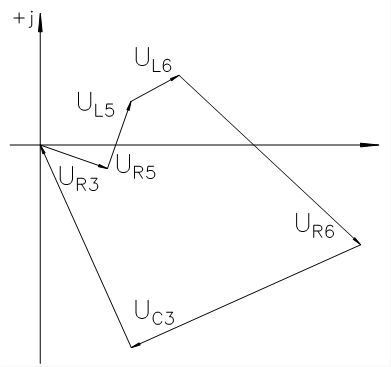
Топографическая диаграмма для 3го контура:
Исследование сложной электрической цепи постоянного тока методом узловых потенциалов. 1
1. Расчет узловых потенциалов. 1
2. Проверка законов Кирхгофа. 2
3. Проверка баланса мощностей в схеме_ 3
4. Метод эквивалентного генератора. 3
5. Построение потенциальной диаграммы по контуру. 4
Исследование сложной электрической цепи переменного тока методом контурных токов. 5
1. Расчет токов и напряжений в схеме, методом контурных токов. 6
2. Проверка баланса мощностей. 6
3. Построение векторной диаграммы и проверка 2го закона Кирхгофа. 7