Реферат: Справочник по геометрии (7-9 класс)

Выполнил:

ученик 9А класса

средней школы № 135

Матвеев Евгений.

Руководитель проекта:

Очеретина Т.В.

Казань 2004 г.

7 класс.

Глава I.

Точки, прямые, отрезки.

Через любые две точки Если две прямые имеют общую

можно провести прямую, точку, то они пересекаются.

и притом только одну.

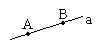
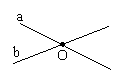
Прямая а и точки А и В.

Прямая а и b пересекаются в точке О.

Две прямые либо имеют только одну общую точку,

либо не имеют общих точек.

Угол.

Угол – это геометрическая фигура, Угол называется развёрнутым, которая состоит из точки и двух лучей, если обе его стороны

исходящих из этой точки. лежат на одной прямой.

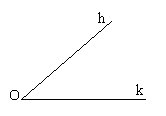
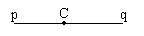
Угол с вершиной О и сторонами h и k. Развёрнутый угол с вершиной С

и сторонами p и q.

Развёрнутый угол = 180є; Неразвёрнутый угол < 180є .

Луч, исходящий из вершины угла и Два угла, у которых одна общая

делящий его на два равных угла, сторона общая, а две другие

называется биссектриса угла. являются продолжениями одна

другой, называются смежными.

Два угла, называются вертикальными,

если стороны одного угла являются Сумма смежных углов = 180є.

продолжениями сторон другого.

Две пересекающиеся прямые

Вертикальные углы равны. называются перпендикулярными,

если они образуют 4 прямых угла.

Глава I I.

Треугольники.

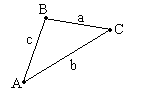
Треугольник – геометрическая фигура, РАВС = АВ+ВС+СА.

кот-ая состоит из 3 точек, не лежа-

щих на 1 прямой, соединённых отрезками.

В равных треугольниках против

Треугольник с вершинами А, В, С и соответственно равных сторон

Сторонами а, b, c. лежат равные углы, также против

соответственно равных равных

углов лежат равные стороны.

Теорема: Если 2 стороны и угол Теорема: Из точки, не лежа-

между ними 1-го треугольника щей на прямой, можно провести

соответственно равны 2 сторонам перпендикуляр к этой, и притом

и углу между ними другого только один.

треугольника, то треугольники равны.

Отрезок, соединяющий вершину треуг- Отрезок бисс-сы угла треуг-ка,

ка с серединой противоположной сто- соединяющий вершину треуг-ка

роны, называется медианой треуг-ка. с точкой противоположной сторо- ны, называется бисс-сой треуг-ка.

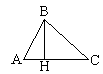
Перпендикуляр, проведённый из верши-

ны треуг-ка к прямой, содержащей Треуг-к, у кот-го 2 стороны равны,

противоположную сторону, называ- называется равнобедренным.

ется высотой треуг-ка.

Теорема: В равнобедренном треуг-ке

ВН - высота треуг-ка АВС. углы при основании равны.

Теорема: В равнобедренном Высота равнобедренного треуг-ка, про-

треуг-ке бисс-са, проведённая ведённая к основанию, является медианой

к основа-нию, является и бисс-сой.

медианой и высотой.

Медиана, проведённая к основанию, явля-

ется высотой и бисс-сой.

Теорема: Если сторона и 2 Теорема: Если три стороны 1го

прилежащих к ней угла 1го треуг-ка соответственно равны 3ём

треуг-ка соответственно рав- сторонам другого треуг-ка, то такие

ны стороне и 2 прилежащим к треуг-ки равны.

ней углам другого треуг-ка, то

такие треуг-ки равны.

Определение: Окружность называется геометр-ая фигура, состоя-щая из всех точек, располож-ых на заданном расс-нии от данной точки.

Глава I I I.

Параллельные прямые.

Определение: Две прямые Теорема: Если при пересечении 2 пря-

на плоскости параллельны, мых секущей накрест лежащие углы рав-

если они не пересекаются. ны, то прямые параллельны.

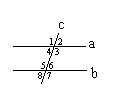Теорема: Если при пересечении 2 пря-

Накрест лежащие – 3 и 5, 4 и 6. мых секущей соответственные углы рав-

Односторонние – 4 и 5, 3 и 6. ны, то прямые параллельны.

Соответственные – 1 и 5, 4 и 8,2 и 6, 3 и 7.

Теорема: Если при пересече- Теорема: Если две параллельные пря-

нии 2 прямых секущей сумма мые пересечены секущей, то накрест

односторонних углов равна лежащие углы равны.

180є, то прямые параллельны.

Теорема: Если две прямые пересечены

Теорема: Если две парал- секущей, то сумма односторонних углов

лельные прямые пересечены равна 180є.

секущей, то соответствен-

ные углы равны.

Глава IV.

Соотношения между сторонами

и углами треугольника.

Теорема: Сумма углов Внешний угол треуг-ка = сумме двух углов тре-

треуг-ка = 180є. уг-ка, не смежных с ним.

В любом треугольнике либо Теорема: В треуг-ке против большей сто-

все углы острые, либо два роны лежит больший угол, против большего

два угла острые, а третий угла лежит большая сторона.

тупой или прямой.

В прямоугольном треуг- ке гипотенуза Если два угла треуг-ка равны, то больше катета. треуг-к – равнобедренный.

Теорема: Каждая сторона Для любых 3 точек А,В,С, не лежащих на

треугольника меньше суммы одной прямой, справедливы неравенства:

2 других сторон. АВAB+BC, ВС

Сумма двух острых углов пря- Катет прямоугольного треуг-ка, лежащий

моугольного треуг-ка = 90є. против угла в 30є, равен Ѕ гипотенузы.

Если катет прямоугольного треуг- Если катеты 1го прямоугольного треуг-

ка = Ѕ гипотенузы, то угол, лежа- ка соответственно = катетам другого

щий против этого катета, = 30є. , то такие треуг-ки равны.

Если катет и прилежащий к нему Теорема: Если гипотенуза и острый

острый угол 1го прямоугольного угол 1го прямоугольного треуг-ка соот-

треуг-ка соответственно равны ветственно равны гипотенузе и остро-

катету и прилежащему к нему му углу другого, то такие треуг-ки равны. острому углу другого, то такие

треугольники равны. Теорема: Если гипотенуза и катет 1го

прямоугольного треуг-ка соответствен-

Теорема: Все точки каж- но равны гипотенузе и катету другого,

дой из 2 параллельных прямых то такие треугольники равны.

равноудалены от другой прямой.

Расстояние от произвольной точки 1ой из параллельных прямых до

другой прямой называется прямой называется расстоянием между

этими прямыми.

8 класс.

Глава V.

Многоугольники.

Сумма углов выпуклого n-угольника В параллелограмме противоположные

= (n-2)180є. стороны равны и противоположные

углы равны.

Диагонали параллелограмма точ-

кой пересечения делятся пополам. Если в 4-угольнике 2 стороны равны и

параллельны, то этот 4-угольник – па-

раллелограм.

Если в 4-угольнике противопо-

ложные стороны попарно равны, Если в 4-угольнике диагональю пересе-

то этот 4-угольник – параллело- каются и точкой пересечения делятся

грамм. пополам, то этот 4-угольник – парал-

лелограмм.

Трапецией называется 4-угольник,

у кот-го 2 стороны параллельны, а Прямоугольником называется парал-

2 другие стороны не параллельны. лелелограмм, у кот-го все углы прямые.

Диагонали прямоугольника равны. Если в параллелограмме дигонали равны,

то этот параллелограмм – прямоуголь-

Ромбом называется параллело- ник.

грамм, у кот-го все стороны

равны. Диагонали ромба взаимно перпендикуляр-

ны и делят его углы пополам.

Квадкатом называется прямо-

угольник, у кот-го все стороны Все углы квадрата равны.

равны.

Диагонали квадрата равны, взаимно

Фигура называется симметричной перпендикулярны, точкой пересечения

относительно прямой а, если для делятся пополам и делят углы

каждой точки фигуры симметричная квадрата пополам.

ей точка относительно прямой а

также принадлежит этой фигуре. Прямая а называется осью симметрии.

Фигура называется симметричной Точка О называется центром симмет-

относительно точки О, если для рии фигуры.

каждой точки фигуры симметрич-

ная ей точка относительно точки О

также принадлежит этой фигуре.

ГлаваVI.

Площадь.

Равные многоугольники имеют S квадрата равна квадрату его стороны.

Равные S.

Если многоугольник составлен из Теорема: S прямоугольника = про-

нескольких многоугольников, то изведению его смежных сторон.

Его S = сумме площадей этих

многоугольников. Теорема: S параллелограмма = про-

изведению его основания на высоту.

Теорема: S треугольника =

= произведению его основания S прямоугольного треугольника = 1/2

на высоту. произведения его катетов.

Если высоты 2ух 3-угольников Теорема: Если угол 1го 3-угольника

равны, то их S относятся равен углу другого 3-угольника, то S

как основания. этих 3-угольников относятся как про-

изведения сторон, заключающих равные

Теорема: S трапеции = про- углы.

изведению полусуммы её осно-

ваний на высоту. Теорема: В прямоугольном 3-угольни-

ке квадрат гипотенузы = сумме квадра-

Теорема: Если квадрат 1ой тов катетов.

стороны 3-угольника = сумме

квадратов 2 других сторон, то

3-угольник прямоугольный.

ГлаваVII.

Подобные треугольники.

Определение: 2 3-угольника Теорема: Отношение S 2ух подоб-

называются подобными, если их ных 3-угольников = квадрату коэф-

углы соответственно равны и фициента подобия.

стороны 1го 3-угольника про-

порционально сходственны Теорема: Если 2 угла 1го 3-уголь-

сторонам другого. ника соответственно = 2ум углам

другого, то такие 3-угольники по-

Теорема: Если 2 стороны 1го добны.

3-угольника пропорциональны 2ум

сторонам другого 3-угольника и углы, заключённые между этими сторо-

нами, равны, то такие 3-угольники подобны.

Теорема: Если 3 стороны 1го Теорема: Средняя линия параллель-

3-угольника пропорциональны на 1ой из его сторон и равна Ѕ этой

3ём сторонам другого, то такие стороны.

3-угольники подобны.

sin острого угла прямоугольного cos острого угла прямоугольного 3-уголь-

3-угольника – отношение ника – отношение прилежащего катета

противолежащего катета к к гипотенузе.

гипотенузе.

tg угла = отношению sin к cos

tg острого угла прямоугольного этого угла: tg = sin/ cos.

3-угольника – отношение противо-

лежащего катета к прилежащему. Основное тригонометрическое

тождество:

Если острый угол 1го прямоугольного sin2α+ cos2α=1.

3-угольника = острому углу другого прямо-

угольного 3-угольника, то синусы, косинусы и тангенсы этих углов равны.

x

0°

30°

45°

60°

90°

180°

270°

360°

sinx

0

1/2

2/2

3/2

1

0

-1

0

cosx

1

3/2

2/2

1/2

0

-1

0

1

tgx

0

1/ 3

1

3
—
0
—
0

ctgx
—
3

1

1/ 3

0
—
0
—

0

П/6

П/4

П/3

П/2

П

3П/2

2П

Глава VIII.

Окружность.

Если расстояние от центра окруж- Если расстояние от центра окруж-

ности до прямой < радиуса, то пря- ности до прямой = радиуса, то пря-

мая и окружность имеют 2 общие мая и окружность имеют 2 общие

точки. Прямая является секущей. точки. Прямая является касательной.

Если расстояние от центра окруж- Теорема: Касательная к окруж-

ности до прямой > радиуса, то пря- ности перпендикулярна к r, прове-

мая и окружность не имеют общих дённому в точку касания.

точек.

Теорема: Если прямая проходит

Отрезки касательных к окружнос- через конец r, лежащий на окруж-

ти, проведённые из 1ой точки, рав- ности, и перпендикулярна к этому

ны и составляют равные углы с r, то она является касательной.

прямой, проходящей через эту точ-

ку и центр окружности. Дуга является полуокружностью.

Угол с вершиной в центре окруж- Если дуга АВ окружности с центром

ности — её центральный угол. О < полуокружности или является

полуокружностью, то её градусная

Сумма градусных мер 2ух дуг ок- мера считается равной градусной

ружности с общими концами = мере центрального угла АОВ. Если же

= 360°. дуга АВ > полуокружности, то её

градусная мера считается =

Угол, вершина кот-го лежит на = 360°–

окружности, а стороны пересе-

кают окружность, называется Теорема: Вписанный угол измеряя-

вписанным углом. ется Ѕ дуги, на кот-ую он опирается.

Луч ВО совпадает с 1ой из сто- Луч ВО делит угол АВС на 2 угла, если

рон угла АВС. луч ВО пересекает дугу АС.

Луч ВО не делит угол АВС на 2 Вписанные углы, опирающиеся на 1 и ту

угла и не совпадает со сторона- же дугу, равны.

ми этого угла, если луч ВО не

пересекает дугу АС. Вписанный угол, опирающийся на полу-

окружность, -- прямой.

Теорема: Если 2 хорды ок- Теорема: Каждая точка бисс-сы

ружности пересекаются, то неразвёрнутого угла равноудалена

произведение отрезков 1ой от его сторон. Каждая точка, ле-

хорды = произведению отрез- жащая внутри угла и равноудалённая

ков другой хорды. от сторон угла, лежит на его бисс-се.

Бисс-сы 3-угольника пересека- Серединным перпендикуляром к отрезку

ются в 1ой точке. называется прямая, проходящая через

середину отрезка и перпендикулярная

Теорема: Каждая точка се- к нему.

рединного перпендикуляра к

отрезку равноудалена от концов Серединные перпендикуляры к сторо-

этого отрезка. Каждая точка, нам 3-угольника пересекаются в 1ой

равноудалённая отконцов отрез- точке.

ка, лежит на серединном перпен-

дикуляре. Теорема: в любой 3-угольник мож-

но вписать окружность.

Теорема: Высоты 3-угольника

(или их продолжения) пересека- В 3-угольник можно вписать только 1у

ются в 1ой точке. окружность.

Теорема: Около любого треу- В любом вписанном 4-угольнике сумма

гольника можно онисать окруж- противоположных углов = 180°.

ность.

Если сумма противоположных углов 4-угольника = 180°, то около него можно описать окружность.

Глава IX.

Векторы.

Физические величины, характери- Определение: Отрезок, для кот-

зуещиеся направлением в прост- го указано, какой из его концов счи-

ранстве – векторные. тается началом, а какой – концом,

называется вектором.

Длина (модуль) – длина АВ.

Длина нулевого вектора = 0.

Нулевые векторы называются

коллинеарными, если они лежат Если 2 вектора направлены одинаково,

либо на одной прямой, либо на то эти векторы – сонаправлены.

параллельных прямых; нулевой

вектор считается коллинеар- Если 2 вектора направлены противопо-

ным любому вектору. ложно, то они противоположно напра-

влены.

Определение: Векторы,

называются равными, если От любой точки М можно отложить

они сонаправлены и их дли- вектор, равный данному вектору г, и

ны равны. притом только один.

Теорема: для любых векторов ă, č и ĕ справедливы равенства:

ă + č = č + ă (переместительный закон);

( ă + č )+ ĕ = ă +( č + ĕ ).

Теорема: Для любых векто- Произведение любого вектора на число

ров ă и č справедливо равенство: 0 есть нулевой вектор.

ă – č = ă + ( - č ).

Для любого числа k и любого векто- ( kl )ă=k( lă ) (сочетательный закон);

ра ă векторы ă и kă коллинеарны. ( k+ l )ă=kă+lă(1ый рспред-ный закон);

k(ă+č )=kă+kč.

Теорема: Средняя линия тра-

пеции параллельна основаниям

и = их полусумме.

9 класс.

Глава X.

Метод координат.

Лемма: Если векторы ă и č Теорема: Любой вектор можно раз-

коллинеарны и ă=0, то сущес- ложить по 2ум данным неколлинеар-

твует такое число k, что č=kă. ным векторам, причём коэффициен-

ты разложения определяются един-

Каждая координата суммы 2ух ственным образом.

векторов = сумме соответству-

ющих координат этих векторов. Каждая координата произведения век-

тора на число = произведению соот-

Каждая координата разности ветствующей координаты вектора

2ух векторов = разности соот- на это число.

ветствующих координат век-

тора на это число. Координаты точки М = соответству-

ющим координатам её радиус-вектора.

Каждая координата вектора =

разности соответствующих ко- Каждая координата середины отрезка

ординат его конца и начала. равна полусумме соответствующих ко-

ординат его концов.

Глава XI.

Соотношения между сторонами

и углами 3-угольника.

Скалярное произведение

векторов.

Для любого угла α из промежут- tg угла α(α=90°) называется отношение

ка 0° sin угла α называ- sinα/cosα.

ется ордината у точки М, а cos

угла α – абсцисса х угла α. sin(90°-- α)= cos α

Теорема: S 3-угольника = Ѕ Теорема: Стороны 3-угольника про-

произведения 2ух его сторон на порциональны sin противолежащих

sin угла между ними. углов.

Теорема: Квадрат стороны 3-угольника = сумме квадратов 2ух других сторон – удвоенное произведение этих сторон на cos угла между ними.

а2=b2+с2-2bс cos α.

Скалярным произведением 2ух Скалярный квадрат вектора = квадра-

векторов называется произве- ту его длины.

дение их длин на cos угла между

ними.

Теорема: Скалярное произведение векторов а( х1; у1) и b( х2; у2 ) выражается формулой:

ab=х1 х2 +у1 у2.

Нулевые векторы а( х1; у1) и cos угла а между нулевыми векторами

b( х2; у2 )перпендикулярны а( х1; у1) и b( х1; у1) выражается формулой:

тогда и только тогда, ког- cos α= х1 х2 +у1 у2 / х1+у1 х2 + у2.

да х1 х2 + у1 у2 = 0.

Для любых векторов а, b, с и любого числа k справедливы соотношения:

а2>0, причём а2>0 при а=0.

аb=bа (переместительный закон).

( а+ b )с=ас+ bс (распределительный закон).

( kа )b=k( ab) (сочетательный закон).