Реферат: Моделирование систем управления

Южно Уральский Государственный Университет

Кафедра “Автоматики и телемеханики”

К У Р С О В А Я Р А Б О Т А

По теме “Моделирование систем управления”

Вариант № 17

Выполнила: Киселева Е.В.

Группа 421

Проверил: Стародубцев Г.Е.

Миасс, 1999 г.

Задание на курсовое проектирование

1. Провести полный факторный эксперимент вида 3^3 с моделью BLACK BOX

2. Методом регрессионного анализа получить аналитическую зависимость

y=f(x1,x2,t)

3. Составить модель полученного уравнения регрессии.

4. Провести оценку адекватности уравнения регрессии заданной модели по критерию Фишера для a=0,05 , рассчитать среднее абсолютное отклонение координат аналитической модели от заданной.

5. Провести оценку значимости коэффициентов регрессии по критерию Стьюдента для a=0,05

6. Получить графики ошибки

ym-yr=f(t)

ym - выходная координата модели BLACK BOX

yr - выходная координата созданной модели

Значения параметров:

x1= 0.6 ... -1.4

x2= 2.0 ... 0.6

t = 2 ... 10

b = 1.1

Экспериментальные данные.

1. Составим последовательность имитации эксперимента, исходя из данных курсового задания, и представим в матричной форме. Имитационная модель – это модель системы управления с введением случайной переменной погрешности b=1,1.

Необходимо найти аналитическое уравнение связи параметров системы и числовых знаковых коэффициентов. Уравнение регрессии имеет следующий вид:

Y=b0+Sbixi+Sbijxixj+Sbiixi2

bixi – линейная регрессия,

bijxixj- неполная квадратичная регрессия,

biixi2- квадратичная регрессия.

Схема для проведения экспериментов (приложение №1 Vissim 32)

Матричная форма имитационного эксперимента.

x0	x1	x2	x3=t	x1*x2	x1*x3	x2*x3	x1*x1	x2*x2	x3*x3
1	0,6	2	10	1,2	6	20	0,36	4	100
1	0,6	2	6	1,2	3,6	12	0,36	4	36
1	0,6	2	2	1,2	1,2	4	0,36	4	4
1	0,6	1,3	10	0,78	6	13	0,36	1,69	100
1	0,6	1,3	6	0,78	3,6	7,8	0,36	1,69	36
1	0,6	1,3	2	0,78	1,2	2,6	0,36	1,69	4
1	0,6	0,6	10	0,36	6	6	0,36	0,36	100
1	0,6	0,6	6	0,36	3,6	3,6	0,36	0,36	36
1	0,6	0,6	2	0,36	1,2	1,2	0,36	0,36	4
1	-0,4	2	10	-0,8	-4	20	0,16	4	100
1	-0,4	2	6	-0,8	-2,4	12	0,16	4	36
1	-0,4	2	2	-0,8	-0,8	4	0,16	4	4
1	-0,4	1,3	10	-0,52	-4	13	0,16	1,69	100
1	-0,4	1,3	6	-0,52	-2,4	7,8	0,16	1,69	36
1	-0,4	1,3	2	-0,52	-0,8	2,6	0,16	1,69	4
1	-0,4	0,6	10	-0,24	-4	6	0,16	0,36	100
1	-0,4	0,6	6	-0,24	-2,4	3,6	0,16	0,36	36
1	-0,4	0,6	2	-0,24	-0,8	1,2	0,16	0,36	4
1	-1,4	2	10	-2,8	-14	20	1,96	4	100
1	-1,4	2	6	-2,8	-8,4	12	1,96	4	36
1	-1,4	2	2	-2,8	-2,8	4	1,96	4	4
1	-1,4	1,3	10	-1,82	-14	13	1,96	1,69	100
1	-1,4	1,3	6	-1,82	-8,4	7,8	1,96	1,69	36
1	-1,4	1,3	2	-1,82	-2,8	2,6	1,96	1,69	4
1	-1,4	0,6	10	-0,84	-14	6	1,96	0,36	100
1	-1,4	0,6	6	-0,84	-8,4	3,6	1,96	0,36	36
1	-1,4	0,6	2	-0,84	-2,8	1,2	1,96	0,36	4

Матрица значений полученных в результате эксперимента.

y0	y1	y2	y3	y4	Ysr
235,09	235,41	235,727	234,95	236,37	235,51
134,71	136,34	136,881	135,22	135,76	135,78
67,067	68,544	67,82	68,197	68,574	68,04
140,38	140,7	141,017	140,24	141,66	140,8
60,996	62,634	63,171	61,508	62,046	62,071
14,357	15,834	15,11	15,487	15,864	15,33
64,287	64,606	64,926	64,146	65,565	64,706
5,906	7,544	8,081	6,418	6,956	6,981
-19,73	-18,26	-18,979	-18,6	-18,23	-18,759
100,25	100,57	100,887	100,11	101,53	100,67
65,866	67,504	68,041	66,378	66,916	66,941
64,227	65,704	64,98	65,357	65,734	65,2
-9,162	-8,843	-8,523	-9,303	-7,884	-8,743
-22,54	-20,91	-20,368	-22,03	-21,49	-21,468
-3,182	-1,705	-2,429	-2,052	-1,675	-2,2086
-99,95	-99,63	-99,313	-100,1	-98,67	-99,533
-92,33	-90,7	-90,158	-91,82	-91,28	-91,258
-51,97	-50,5	-51,219	-50,84	-50,47	-50,999
-53,19	-52,87	-52,553	-53,33	-51,91	-52,773
-21,57	-19,94	-19,398	-21,06	-20,52	-20,498
42,787	44,264	43,54	43,917	44,294	43,76
-177,3	-177	-178,663	-177,4	-176	-177,28
-124,7	-123	-122,509	-124,2	-123,6	-123,61
-39,32	-37,85	-38,569	-38,19	-37,82	-38,349
-282,8	-282,5	-282,153	-282,9	-281,5	-282,37
-209,2	-207,5	-206,999	-208,7	-208,1	-208,1
-102,8	-101,3	-102,059	-101,7	-101,3	-101,84

Вычислим коэффициенты B по формуле

B=(XTX)-1XTYsr

XT – транспонированная матрица

Ysr- средние экспериментальные значения

b0	-29,799251
b1	13,6541852
b2	9,96405181
b3	-15,946707
b4	-21,000048
b5	16,508325
b6	7,50010119
b7	-9,3224778
b8	19,0904535
b9	0,99813056

Вычисления производились в Microsoft Excel по следующей формуле

=МУМНОЖ(МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП (Хматрица);Хматрица));ТРАНСП(Хматрица));Yматрица)

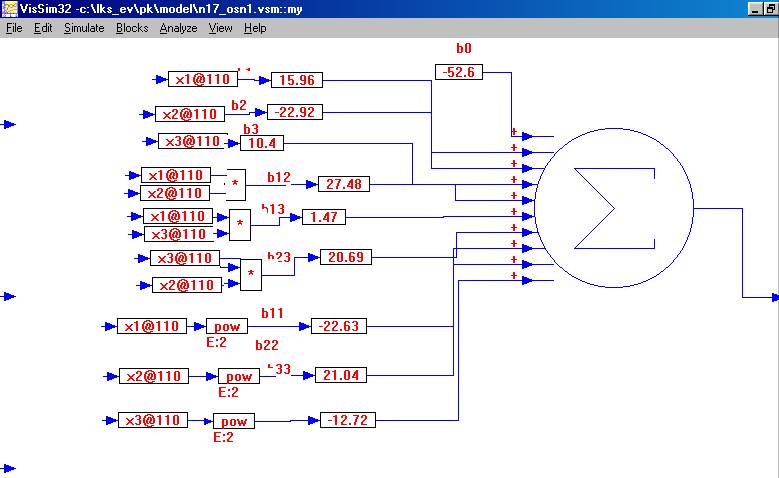
Полученные коэффициенты подставим в уравнение регрессии и построим схему для проведения эксперимента (приложение №2,3 Vissim 32) и проведем эксперимент без использования дельты или шума.

Внесем полученные данные в столбец (Yip) таблицы.

Ysr	Si кв	Yip	(Yi-Yip)2
235,51	0,3219	234,7	0,61090
135,78	0,7492	135,5	0,06574
68,04	0,3897	68	0,00163
140,8	0,3219	140	0,68327
62,071	0,75	61,77	0,09060
15,33	0,3897	15,25	0,00646
64,706	0,3214	63,93	0,60218
6,981	0,75	6,73	0,06300
-18,759	0,3897	-18,78	0,00046
100,67	0,3219	99,93	0,54258
66,941	0,75	66,73	0,04452
65,2	0,3897	65,21	0,00009
-8,743	0,3214	-9,51	0,58829
-21,468	0,75	-21,71	0,05856
-2,2086	0,3897	-2,23	0,00046
-99,533	0,3216	-100,3	0,51380
-91,258	0,75	-91,45	0,03686
-50,999	0,3897	-50,97	0,00082
-52,773	0,3214	-53,48	0,49985
-20,498	0,75	-20,68	0,03312
43,76	0,3897	43,79	0,00088
-177,28	0,9015	-177,6	0,12013
-123,61	0,7492	-123,8	0,04902
-38,349	0,3897	-38,35	0,00000
-282,37	0,3219	-283,1	0,48525
-208,1	0,7492	-208,3	0,02938
-101,84	0,3892	-101,8	0,00240
SSi=13,73			S=5,13026

Так как результаты опытов обладают статической неопределенностью, поэтому опыты воспроизводим несколько раз при одних и тех же значениях факторов для повышения точности коэффициентов регрессии за счет эффекта понижения дисперсии.

n=27- экспериментов

m=10 – количество членов уравнения

Si2=1/g-1*S(Ygi-Yi)2 , g- количество экспериментов ( 5)

Sy2=1/n*SSi2

S0= å(Yi-Yip)2/n-m – среднеквадратичная ошибка на степень свободы

d=å|Yi-Yip|/n – среднее обсолютное отклонение между расчетными значениями

Адекватность вида регрессии уравнения определяется по критерию Фишера, а значимость коэффициентов по критерию Стьюдента и доверительного интервала на его основе.

Fрасч= S02/Sy2<Fтабл(a, n-m)

Fтабл=1,77 ,

a=0,05 – уровень значимости

1-a®р – вероятность с которой уравнение будет адекватно.

n-mÞ27-10=17 – число степеней свободы

SDbj2=Sy2/n - дисперсия коэффициентов взаимодействия

Dbj=±tc* Ö Sy2/ Ö n

tc=2,12

Sy2	0,5085	Fрасч.	1,08031201
So	0,5493	Sg2	0,01883355
d	0,4359	Dbj	0,29093901
		p	0,95

Fтабл=1,75> Fрасч.= 1,08, значит система адекватна.

Уравнение регрессии примет вид.

Y=-29,79+13,65x1+9,96x2-15,94x3-21x1x2+16,5x1x3 +7,5x2x3-9,32x12+19,09x22+0,99x32

График ошибки (см. приложение № 4).

Вывод.

Исходя из полученных значений сделаем вывод, что полученная система очень мало отличается от заданной.

Уравнения адекватны

Коэффициенты значимы

Приложение № 1

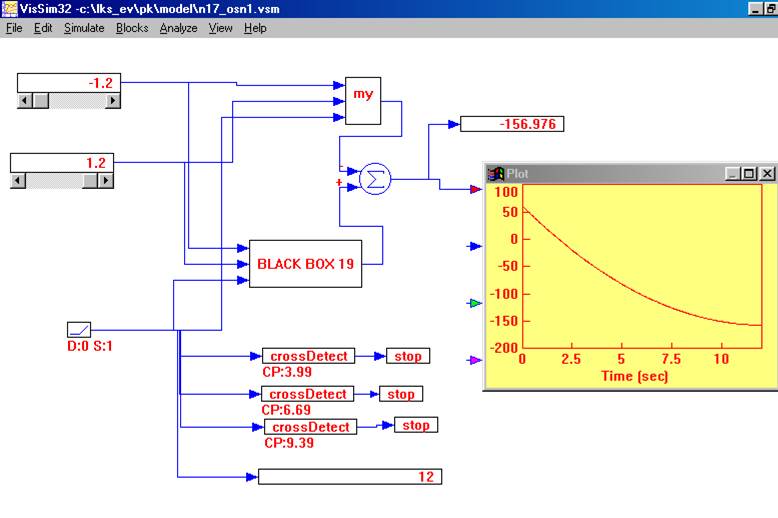
Приложение № 2