Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Реферат: Методические основы уровневой дифференциации при обучении алгебре в классах с углубленным изучением математики
Реферат: Методические основы уровневой дифференциации при обучении алгебре в классах с углубленным изучением математики
Министерство просвещения ПМР
Приднестровский государственный университет
им. Т. Г. Шевченко
физико-математический факультет
Допустить к защите
зав. кафедрой
![]() Гайдаржи
Гайдаржи
![]()
![]() «
» 2002 г.
«
» 2002 г.
ДИПЛОМНАЯ РАБОТА
Тема: Методические основы уровневой дифференциации при обучении алгебре в классах с углубленным изучением математики
Научный руководитель:
Герасимова А. Д.
Выполнила:
Студентка заочного отделения группы № 52
Предеина Елена Юрьевна
Тирасполь 2002 г.
СОДЕРЖАНИЕ
Введение.
Глава 1. Дифференциация в истории школы
математического
образования.
1.1 Основные понятия теории
дифференцированного обучения.
. 1.2 Дифференциация как система
1.3 Индивидуальные особенности
учащихся и их учет в процессе
обучения математики.
Типологические группы учащихся.
1.4 Организация дифференцированного
подхода в обучении математики.
1.5 Отбор учащихся в классы с углубленным
изучением математики.
Глава 2. Методические основы уровневой
дифференциации.
2.1 Фронтальная работа.
2.2 Групповая работа.
2.3 Индивидуальная работа учащихся.
2.4 Критерии оценки знаний учащихся.
Заключение.
Список использованной литературы.
Введение.
Наше время ставит перед школой задачу – повышение качества образования и воспитания, прочное овладение основами наук, обеспечение более высокого научного уровня преподавания каждого предмета. В школах отказываются от традиционной формы обучения, не учитывающей индивидуальных способностей каждого ученика. Обновление образования требует разработки моделей школ нового типа, создания новых учебников и программ обучения, разработки новых методик обучен6ия. Поднять работу школы на новый уровень можно путем индивидуализации обучения, создания таких условий, при которых каждый школьник мог бы полностью овладеть установленным программами образовательным минимумом, который в первом приближении дан в вышедших в августе 1993 года государственных стандартах общего среднего образования, подчеркивающих роль уровневой дифференциации в ходе обучения.
Анализ психолого-педагогической литературы показывает, что дифференциация обучения как общая педагогическая задача не является новой ни для нашей, ни для зарубежной школы. Необходимо отметить работы в этом направлении педагогов: Бабанского Ю.К., Кирсанова А.А., Лернева И.Я., Рабунского Е.С., Скаткина Н.М., Унт И.Э. и других; психологов: Выгодского С.Л., Гальперина П.Я., Давыдова В.В., Крутецкого В.А., Менчинской Н.А., Талызиной Н.Ф., Фридмана Л.М. и других; методистов: Гусева В.А., Капеносова А.Н., Куприяновича В.В., Метельского Н.В., Слепкань З.И., Смирновой И.М. Столяра А.А. и других. Довольно много разработок в этой области принадлежит математикам Болтянскому В.Г., Дорофееву Г.В., Калягину Ю.М. и другим.
В современных условия важно осознать и принять принципиальную педагогическую установку- каждый ученик может добровольно выбрать для себя уровень усвоения и отчетности в результатах своего учебного труда. Обязанностью ученика становится выполнение обязательных требований, что позволяет ему иметь положительную оценку по математике. В то же время ученик получает право самостоятельно решать, ограничиться ли ему уровнем образовательных требований или двигаться дальше. Это кардинально меняет традиционные подходы к организации обучения: не следует решать за ученика, какой уровень усвоения соответствует его способностям, но следует создать в классе такие условия, при которых достижение обязательного уровня будет реальным, ученики, способные двигаться дальше, будут заинтересованы в этом продвижении.
Существующая система обучения в школе пока не отвечает гигиеническим требованиям и не способствует формированию здорового образа жизни. Подросткам приходится осваивать слишком большой объем информации: анализ учебной литературы (учебников, задачников, книг для чтения), конспектов работ показывает, что учащиеся профильных десятых классов должны прочесть около 5500 страниц учебников, литературно-художественных произведений и первоисточников, выучить более 2900 определений, усвоить 1000 понятий. Необходимо добавить сюда еще 300 основных и вспомогательных понятий по профилирующим предметам и решить более200 задач по математике, физике, химии и биологии. Большая дневная нагрузка, сокращение дневного отдыха и ночного сна оказывают отрицательное влияние на здоровье человека. Практика дифференцированного обучения могла бы считаться наиболее эффективной в сравнении с обучением в массовой школе, если бы более высокий уровень знаний и умений обеспечивался при существенном сокращении времени на обучение. Поэтому эта проблема остается пока открытой, учебная нагрузка нуждается в нормализации, а методы преподавания в дальнейшем совершенствовании.
Итак, особое значение для внедрения в практику любых форм и приемов дифференцированного обучения имеет организация предметного содержания учебного материала. Центральное место в нем отводится системам задач, так как они служат основными средствами формирования приемов учебной деятельности учащихся по решению задач. Анализ методических работ показал, что настоящий момент системы школьных математических задач строятся без учета знаний о задаче как сложном объекте, о ее внешнем и внутреннем строении. В исследованиях, посвященных задачам широкое распространение нашел деятельностный подход (Ю.М. Калягин, В.И. Крупич, Г.И. Саранцев). Однако основное внимание уделяется внешней (информационной) структуре задачи ( Ю.М. Калягин, Л.М. Фридман). Знание структуры задачи позволяет решить вопрос о ее сложности и на этой основе строить системы задач, обладающих свойством структурной полноты.
Все вышесказанное обуславливает актуальность проблемы исследования: выявление индивидуальных особенностей учащихся и возможности системы дифференцированных задач в процессе обучения учащихся алгебре.
Объектом исследования является организация процесса обучения учащихся алгебре в классах с углубленным изучением математики.
В ходе исследования была выдвинута следующая гипотеза:
повышение результатов обучения, выявление возможностей построения системы предметных задач с целью повышения эффективности обучения учащихся решению задач курса алгебры.
Для решения поставленной проблемы и проверки сформулированной гипотезы были выдвинуты следующие задачи исследования:
1. Раскрыть психолого-педагогические основы уровневой дифференциации в обучении математике.
2. Сформулировать требования к системе задач, направленной на реализацию уровневой дифференциации.
3. Рассмотреть различные способы организации обучения с целью повышения его эффективности.
Дипломная работа состоит из введения, двух глав (теоретической и методической), заключения и списка литературы.
Глава 1. Дифференциация в истории школы математического образования.
1.1 Основные понятия теории дифференцированного обучения.
В педагогической психологии, дидактике, а также в школьной практике широко используются термины « индивидуальный подход», «индивидуализация обучения», «дифференцированное обучение», «дифференциация образования» и другие. Эти термины нередко употребляются как синонимы, но в то же время в содержании каждого из этих понятий имеются свои существенные признаки.
Продемонстрируем это следующей таблицей, составленной на основании анализа работ в этой области.
Таблица (1.1.1.).
|
Ф. И. О. автора |
Понятия |
|
| Е.С. Рабинский |
1) Индивидуальный подход в учебном процессе означает действенное внимание к каждому ученику, его творческой индивидуальности в условиях классно-урочной системы обучения по общеобразовательным учебным программам и факультативам (в старших классах), предполагает разумное сочетание фронтальных, групповых и индивидуальных занятий для повышения качества обучения и развития каждого школьника. 2) Индивидуализация обучения – особая организация учебного процесса в коллективе класса (группы), которая направлена на осуществление требований индивидуального подхода. 3) Дифференциация образования – разделение учебных планов и программ в старших классах средней школы, осуществляемое на факультативных занятиях, в специализированных школах и классах. 4)Дифференцированный подход – дидактическое положение, предполагающее деление класса на группы, например, по интересам, успеваемости и т.п. 5) Дифференциация обучения = дифференциация учебной работы. Они означают реализацию дифференцированного подхода в обучении, нацеливают на борьбу против ориентации ис5ключительно на учебный класс. |
|
| А.А. Кирсанов |
1) Дифференциация поисков деятельности школьников – предоставление им возможности решать поставленную перед классом познавательную задачу или возникшую перед ним в ходе учебно-практической работе проблему своими путями, своими способами, своим темпом, исходя из уровня подготовленности и познавательных возможностей. 2) Индивидуализация учебной деятельности – система воспитательных и дидактических средств, соответствующих цели деятельности и реальным познавательным возможностям коллектива класса, отдельных учеников и групп учащихся, позволяющих обеспечить учебную деятельность каждого ученика на уровне его потенциальных возможностей с учетом целей обучения. |
|
| И.Э. Унт |
1) Индивидуализация – это учет в процессе обучения индивидуальных особенностей учащихся во всех его формах и методах независимо от того, какие особенности и в какой мере учитываются. 2) Дифференциация – это учет индивидуальных особенностей учащихся в этой форме, когда учащиеся группируются на основании каких-либо особенностей для отдельного обучения, обычно обучение в этом случае происходит по несколько различным учебным плана и программам. |
|
| М.К. Акимова и другие |
1) Индивидуальный подход – ориентация на индивидуально-психологические особенности учеников, включение в работу с ними специальных способов и приемов, соответствующих их индивидуальным особенностям. 2) Внутриклассная индивидуализация обучения – это те приемы и способы индивидуальной работы, которые использует учитель на уроке в обычном классе массовой школы. |
|
| Педагогическая энциклопедия |
Индивидуализация определяется как организация учебного процесса, при котором выбор способов, приемов, темпа обучения учитывает индивидуальные различия учащихся, уровень развития их способностей к обучению. |
|
| А.М. Абрамов и другие |
Дифференциация обучения – создание относительно стабильных или временных учебных групп, различающихся по тем или иным признакам ( содержание, уровень учебных требований, интересы, формы обучения и т.п.) |
|
| Г.В. Дорофеев и другие |
Дифференциация – такая система обучения, при которой каждый ученик, овладевая некоторым минимумом общеобразовательной подготовки, являющейся общезначимой и обеспечивающей возможность адаптации в постоянно изменяющихся условиях, получая право и гарантированную возможность уделять преимущественное внимание тем направлениям, которые в наибольшей степени отвечают его склонностям. |
|
Приведенные высказывания свидетельствуют о тесной взаимосвязи понятий дифференциации и индивидуализации обучения. Это отмечает И.Э. Унт в своей книге «Индивидуализация и дифференциация обучения». В ней говорится о том, что на самом деле в реальной школьной практике стоит говорить об относительной индивидуализации. Относительность она объясняет следующими причинами:
1) Обычно учитываются индивидуальные особенности не каждого отдельного ученика, а в группе учащихся, обладающих примерно сходными особенностями;
2) Учитываются лишь известные особенности или их комплексы, важные с точки зрения учения (общие умственные способности и т.д.); при этом может быть ряд особенностей, учет которых в данной форме индивидуализации невозможен или даже не так уж и необходим (различные свойства характера или темперамента).
3) Иногда учитывают некоторые свойства состояния в том случае, если именно это важно для данного ученика (талантливость в какой-либо области, состояние здоровья и т.д.);
4) Индивидуализация реализуется эпизодически или в каком-либо виде учебной работы и интегрирована с не индивидуализированной работой.
В современной школе одной из возможных форм учета индивидуальных особенностей учащихся является дифференциация обучения.
1.2 Дифференциация как система.
Дифференциацию можно рассматривать с нескольких точек зрения:
1) Процесса обучения (отбор форм, методов и приемов обучения);
2) Содержания образования (создание учебных планов, программ, учебной литературы и составления заданий, предъявляемых учащимся);
3) Построения школьной системы (формирование различных типов школ и классов).
Существует два основных вида дифференциации: уровневая и профильная.
УРОВНЕВАЯ ДИФФЕРЕНЦИАЦИЯ
Уровневая дифференциация выражается в том, что, обучаясь в одном классе, по одной программе и учебнику, школьники могут усваивать материал на разных уровнях.
Концепция уровневой дифференциации – это принципиально новая концепция для нашей страны, Это аналог обучения на основе полного усвоения, которое получило широкое распространение в США, Англии, Австрии, Бельгии, Бразилии, Индонезии, Южной Кореи, Норвегии и других странах.
Фундамент концепции обучения на основе полного усвоения составляют идеи, выдвинутые в 60-е годы американскими психологами Дж. Кэрролом и Б. Блумом. Общественная картина разброса успеваемости обычно объясняется соответствующим разбросом способностей к обучению. Дж. Кэррол обратил внимание на то, что в традиционном учебном процессе всегда фиксированы параметры условий обучения (одинаковые для всех учебное время, способ предъявления информации и т.д.). Единственное, что остается не зафиксированным, - это результат обучения, В таком случае все параметры условий будут меняться, подстраиваясь под достижения всеми учащимися заранее заданного результата.
Этот подход был поддержан и развит Б. С. Блумом. Он предположил, что способности ученика определяются его темпом учения при оптимально подобранных для данного ребенка условиях. Б.С. Блум изучал способности учащихся при изучении разных предметов в условиях, когда время на изучение материала не ограничивается.
Результаты изучения показали, что при правильной организации обучения и, особенно, при снятии жестких временных рамок, около 95% учащихся могут полностью усваивать все содержания обучения.
Реализуя данный подход последователей Дж. Кэррола и Б.С. блума (Дж. Блок, Л. Андерсон и другие) на практике разработали методику обучения на основе полного усвоения. При обучении по этой системе различия в учебных результатах будут иметь место за пределами общего для всех общеобразовательного минимума, под которым будет надстраиваться последующее дифференцированное обучение
Перечислим ряд условий, выполнение которых необходимо для успешного и эффективного осуществления уровневой дифференциации:
1) Выделенные уровни усвоения материала и в первую очередь обязательные результаты обучения должны быть открытыми для учащихся.
Если цели известны и посильны ученику, а их достижения поощряется, то подросток стремится к их выполнению, т. е. формируются положительные мотивы учения, сознательное отношение к учебной работе; можно привлечь самооценку ученика для организации дифференцированной работы.
2) Наличие определенных «ножниц» между уровнем требований и уровнем обучения. Уровень требования должен быть в целом существенно выше, чем обязательный уровень усвоения материала. То есть уровневая дифференциация осуществляется не за счет того, что одним ученикам дают меньше, а другим больше, а в силу того, что , предлагая ученикам одинаковый объем материала, предъявляют различные уровни требований к его усвоению. В силу этого ученик должен иметь учебник, в котором были бы предусмотрены (и явно выделены) все уровни усвоения материала (в том числе и минимально обязательные).
3) В обучении должна быть обеспечена последовательность в продвижении ученика по уровням. То есть не следует предъявлять более высоких требований тем учащимся, которые не достигли уровня обязательной подготовки, но при этом не следует необоснованно задерживать остальных на этом этапе.
4) Содержание контроля и оценка должны отражать принятый уровневый подход. Контроль должен предусматривать проверку достижения всеми учащимися обязательных результатов обучения как государственных требований, а также дополняться проверкой усвоения материала на более высоких уровнях. При этом достижении обязательных результатов целесообразно оценивать «зачтено» - «не зачтено», для более высоких уровней целесообразно соответствующую шкалу оценивания (например, отметка «4», «5»).
5) Добровольность в выборе уровня усвоения и отчетности. Уровневую дифференциацию можно организовать в разнообразных формах. Основной путь осуществления дифференциации обучения – формирование мобильных групп учащихся. По каким же показателям распределять учащихся в группы?
А.Н. Капиносов предложил в качестве таких показателей взять «темп овладения материалом » и «способность самостоятельно применять усвоенные знания и умения». Он выделил четыре группы учеников: с высоким, средним и низким темпом продвижения в обучении; не успевающие учащиеся, значительно отстающие в умственном развитии от сверстников и имеющие существенные пробелы в знаниях.
ПРОФИЛЬНАЯ ДИФФЕРЕНЦИАЦИЯ
Профильная дифференциация (или дифференциация по содержанию) предполагает обучение разных групп школьников по программам, отличающимися глубиной изложения материала, объемом сведений или даже номенклатурой включенных вопросов.
Перечислим основные принципы профильной дифференциации, выделенные на основе анализа отечественного и зарубежного опыта прошлого и настоящего.
1) Обучение по направлениям лишь после того, как школьники получат достаточное единое базовое образование и утвердятся в своих склонностях.
2) На старшей ступени обучения следует обеспечить возможно большее количество направлений обучения или продолжения образования через широкую систему учебных заведений различных типов.
3) По каждому учебному предмету целесообразно объединять различные направления обучения в блоке по принципу сходства целей и задач обучения в этих направлениях для создания единых программ для каждого блока.
4) При составлении программ и учебников, в выборе форм и методов обучения следует учитывать возрастные особенности подростков, склонных к данному виду деятельности, и в то же время не исключать возможности изменить профиль обучения подростку при ошибке в его выборе.
5) Математика должна входить в набор обязательных учебных предметов любого из профилей (физико-математического, технического и гуманитарного). Содержание и объем учебного математического материала должны отражать специфику данного направления.
К блоку обязательных предметов обычно относят следующие четыре предмета: родной язык и литературу, историю и обществоведение, математику и физкультуру. На них должно отводиться не менее 50% учебного времени.
И обязательные предметы, и предметы по выбору предлагается излагать на двух уровнях – общекультурном и повышенном.
Отнесение математики к числу обязательных предметов допускает следующие варианты для ученика:
1) ученик выбирает общекультурный курс и только им и ограничивается;
2) он выбирает повышенный курс, общекультурный при этом не изучает.
Все курсы по двум направлениям – академическому и профессиональному. Академическое направление включает три основных секции: гуманитарную, физико-математическую, естественнонаучную. Профессиональное направление – секциями, имеющими ориентацию на промышленность, сельское хозяйство, сферу обслуживания.
Требования, предъявляемые к математической подготовке учащихся 8-9 классов с углубленным изучением математики, вытекают из ориентационного характера этого этапа. Учащиеся , безусловно, должны владеть всем материалом, входящим в общеобразовательный курс математики, при этом минимальный уровень требований должен совпадать с уровнем требований к учащимся общеобразовательных классов. В то же время достижение учащимися лишь обязательного уровня требований на первом этапе углубленного изучения должно служить сигналом того, что не целесообразно на следующей ступени обучения выбирать профили, связанные с повышенными курсами математики.
Реализация дифференциации может осуществляться различными путями. На основании анализа работ Н.М. Шахмаева, С.В. Алексеева и авторского коллектива, в который вошли А.М. Абрамов, Д.В. Алексеевский, А.М. Гольдман и другие, можно выделить следующие формы дифференциации обучения (см. таблицу 1.2.1).
Исходя из сказанного выше, подчеркнем тот факт, что оба вида дифференциации – уровневая и профильная – взаимосвязаны и сосуществуют на всех ступенях школьного математического образования, однако в разном удельном весе. В основной школе ведущим направлением дифференциации является уровневая, хотя она не теряет своего значения и в старших классах. НА старшей ступени школы приоритет отдается профильной дифференциации, хотя она может уже проявляться и в основной школе, где она осуществляется через систему кружковых занятий и факультативных курсов.
Подводя итог вышесказанному, надо подчеркнуть тот факт, что современный процесс обучения характеризуется двумя неразрывно связанными частями: индивидуально-психологических особенностей каждого ученика, способов и форм реализации дифференцированной работы как с типологическими группами учеников в целом, так и с отдельными учениками. Можно говорить о двустороннем характере этого подхода. При этом индивидуализация определяет обоснованность дифференцированного подхода, а дидактические способы и формы направлены на его практическую реализацию.
Таблица 1.2.1.
![]()
![]() Дифференциация обучения.
Дифференциация обучения.


 Внешняя Внутренняя
Внешняя Внутренняя
![]()
| Самодифференцировка учащихся в соответствии с их уровнем обученности ( по решению задач различной сложности) |
 Спецшколы
Спецшколы
Классы с углубленнымИзучением математики |
|
учитель определяет уровень развития и предлагает учащимся задания, соответствующие их возможностям |

 Факультативы
Факультативы
Альтернативные
|
![]() Математические
кружки
Математические
кружки
|
По математике |
1.3 Индивидуальные особенности учащихся и их учет в процессе обучения математики. Типологические группы учащихся.
В учебной деятельности проявляется широкий диапазон индивидуальных особенностей. Существуют разные классификации, определяемые тем, какие показатели берутся за основу для распределения школьников в группы.
Рассмотрим некоторые из них:
1. А.А. Бударный в качестве основных показателей берет «способность учащихся к учению» и «работоспособность».
А.А. Бударный выделил три группы учеников: с высокими, средними и низкими учебными возможностями. Эти критерии определяют различия учащихся в процессе обучения, но носят довольно общий характер.
2. И.Э. Унт считает, что к особенностям учащихся, которые в первую очередь следует учитывать при индивидуализации обучения, относятся:
1) Обучаемость, то есть общие умственные способности, а также специальные особенности;
2) Учебные умения;
3) Обученность, которая состоит как из программных, так и внепрограммных знаний, умений и навыков;
4) Познавательные интересы (на фоне общей учебной мотивации);
5) Состояние здоровья ребенка.
В отдельных случаях к эти особенностям при индивидуальном подходе к детям добавляются и такие факторы, которые в отношении данного ребенка оказывают специфическое влияние на его учебную деятельность (особенно важны среди этих факторов домашние воспитательные условия).
3.Отклоняя ориентацию на « планируемые результаты обучения», В.Г. Болтянский и Г.Д. Глейзер предложили свою концепцию дифференцированного обучения математике.
Авторы предлагают разделить учащихся по их отношению к курсу математики на три группы, условно уровни знания математики учащимися этих трех групп можно соответственно назвать общекультурным, прикладным и творческим.
1) Общекультурный уровень.
Эту группу должны составлять школьники, для которых математика является лишь элементом общего развития и в их дальнейшей производственной деятельности применяется в незначительном объеме. Для этой категории учащихся существенно овладение общематематической культурой.
2) Прикладной уровень.
В эту группу могут входить учащиеся, для которых математика будет важным инструментом в их профессиональной деятельности. Для этой категории учащихся существенны, наряду со знаниями о математических фактах, навыками логического мышления и пространственными представлениями, прочие навыки решения математических задач.
3) Творческий уровень.
Эту группу должны составлять учащиеся, которые берут математику (или близкие к ней области знания) в качестве основы своей будущей деятельности. Учащиеся этой группы проявляют повышенный интерес к изучению математики и должны творчески овладеть ее основами.
4. Л.В. Виноградова считает, что в качестве основного критерия может быть принят уровень развития мышления, так как необходимо организовать индивидуальный подход так, чтобы он не просто обеспечивал усвоение знаний, но и способствовал бы развитию учащихся.
В пользу выделения в качестве основного именно этого фактора говорят следующие аргументы. У школьников по-разному развиты мыслительные операции, сформированы приемы умственной деятельности, у каждого учащегося своя «зона ближайшего развития». В.С. Цетлин и Е.С. Рабунский в своих работах говорят о том, что основной причиной отставания в обучении у большинства не успевающих школьников является более низкий, чем у сверстников, уровень развития мышления. Поэтому на первый план в работе с не успевающими выдвигается развитие познавательной самостоятельности.
По данным психологов, у детей с пониженной обучаемостью нет патологических изменений в памяти, не связанной с мышлением, но страдает логическая смысловая память. При соответствующих условиях (на нейтральных методиках) слабые ученики концентрируют свое внимание одинаково с сильными. Но внимание является вторичным явлением, его нельзя считать первопричиной возникновения трудностей; оно само обусловлено тем, что ученик в силу особенностей своего мышления не вовлечен в активную учебную работу, ему трудно участвовать в ней.
Активность учащихся, которая заключается в усиленной деятельности в том, что надо не просто смотреть, а видеть, не слушать, а слышать, понимать, осмысленно пользоваться мыслительными операциями, приемами умственной работы, также зависит от развития мышления. Уровень практических действий и у сильных, и у слабых школьников практически одинаков. Но там, где обобщение протекает в словесно-логическом плане, где требуется формировать признаки или искать зависимости, и возникают трудности, обнаруживаются различия между учащимися. Мотивация, отношение к учению также во многом зависят от того, как ученик справляется с работой, получает ли от нее удовлетворение или нет.
5. В.В. Куприянович в качестве основных показателей берет «быстроту усвоения».
В соответствии с этим В.В. Куприянович выделил три группы (таблица 1.3.1.).
Таблица 1.3.1.
|
Уровень |
Быстрота усвоения |
Активность мышления |
|
А: Учащиеся, имеющие хорошие математи-ческие способности |
1. Дословное повторение текста. 2. Частичное повторение. 3. Воспроизведение 50 % текста. 4. Самостоятельное воспроизведение ранее изученного текста. |
1. Плодотворная работа на протяжении всего урока. 2. Работа со «вспышками». |
|
В: Учащие, имеющие средние математи-ческие способности |
4.Самостоятельное воспроизведение ранее изученного текста. 5. Воспроизведение материала с помощью учителя. 6. Воспроизведение с ошибками, но основная нить вопроса выдерживается. |
2. Работа со «вспышками». 3. Неполная работоспособность. |
|
С: Учащие, имеющие низкие математи-ческие способности |
7. Замедленное, невнятное воспроизведение текста. 8. Умственная отсталость (затухание развития). |
4. Быстрая утомляемость. 5. Игнорирование заданий. |
6. А.Н. Капиносов считает, что «объективно существующие различия учащихся в темпах овладения учебным материалом, а также способностях самостоятельно применять усвоенные знания и умения» обуславливает необходимость дифференцированного обучения математики. С учетом этих факторов А.Н. Капиносов выделил четыре «условных» группы:
Первая группа – учащиеся с высоким темпом продвижения в обучении: общие схемы выполнения типовых или усложненных задач, предполагающих применение нескольких известных способов решения.
Вторая группа – учащиеся со средним темпом продвижения в обучении: овладение новыми знаниями и умениями не вызывает особых затруднений, способы выполнения типовых задач усваивают после рассмотрения 2-3 образцов; решения измененных и усложненных задач находят, опираясь на указания учителя.
Третья группа – учащиеся с низким темпом продвижения: при усвоении нового материала испытывают определенные затруднения, во многих случаях нуждаются в дополнительных разъяснениях, обязательными результатами обучения овладевают после достаточно длительной тренировки, способностей к самостоятельному нахождению решений измененных и усложненных задач, как правило, не проявляют.
Четвертая группа – не успевающие учащиеся, значительно отстающие в умственном развитии от сверстников и имеющие существенные пробелы в знаниях. Достижение учащимися этой группы даже уровня обязательных результатов представляет сложную педагогическую задачу.
В заключение этого пункта, что в практической деятельности учителю на уроке затруднительно ориентироваться на многие факторы, практически он не может организовать одновременно работу более чем с 2-3 группами. Следовательно, и класс не может быть разбит более чем на 2-3 группы, - чтобы имелась возможность управления деятельностью в этих группах.
Для организации дифференцированного подхода учителю необходимо следующее: иметь представление об особенностях мыслительной деятельности разных групп учащихся; о путях развития мышления; уметь оценивать уровень развития учащихся; уметь оказывать помощь разной меры при затруднениях учеников; владеть формами организации индивидуального подхода с учетом необходимости развития мышления.
1.4 Организация дифференцированного подхода в обучении математики.
Рассмотрим второе условие осуществления дифференцированного подхода в обучении – определение конкретных направлений его реализации: дифференциация содержания учебного материала, методов и форм обучения; совершенствование способов организации учебной деятельности.
ДИФФЕРЕНЦИАЦИЯ СОДЕРЖАНИЯ ОБУЧЕНИЯ.
Предложенная С.В.Алексеевым дифференциация содержания обучения не будет понятна, если ее не рассмотреть детально. В своей работе он определяет так основные направления работы учителя при осуществлении дифференцированного подхода в обучении:
1) деление класса на группы учащихся, различающихся успешностью обучения;
2) определение трудностей предлагаемого задания.
По мнению С.В. Алексеева целесообразно различать следующие три уровня:
На первом уровне учащиеся воспроизводят знания в том виде, как они изложены в учебнике или были первоначально раскрыты учителем.
Второй уровень характеризуется применением знаний и умений по образцу в повторяющейся учебной ситуации.
Для третьего уровня характерно творческое применение знаний и умений в новой учебной ситуации (см. таблицу 1.4.1.).
Экспресс-информация 3-го уровня представляет собой сообщение (15 мин.) требующее серьезной глубокой проработки источников информации с цель не только изложения публикуемых данных, но и постановкой проблемы для обсуждения.
Заслуживает внимания следующая форма обучения математике – «экспресс - информация». В зависимости от уровня дифференциации эта форма представляет собой следующее:
На 1-ом уровне экспресс – информация представляет собой небольшие (5 мин.) сообщения по темам, требующие репродуктивного воспроизведения известных исторических данных, необходимых для проведения данного урока по данной теме, например, история теоремы Пифагора.
Экспресс – информации 2-го уровня предполагают сообщения требующие определенного времени поиска, ознакомления с современной научно-популярной литературой и умения этот достаточно большой материал сконцентрировать в небольшое сообщение (10-15 мин.
Таблица 1.4.1.
Дифференциация содержания обучения, используемого в математике.
|
Виды учебной информации |
Уровень дифференциации |
||
|
Изложение нового учебного материала. Дифференцированные задания
|
Учащиеся с низкой успеш-ностью обучения |
Учащиеся со средней успеш- ностью обучения |
Учащиеся с высокой успеш- ностью обучения |
| Базовый уровень | Объем программы | Сверх- програм- мный материал | |
|
Классные и домашние Разной сложности по содержанию: а) теоретические; б) расчетные; в) экспериментальные |
Репродук- тивный | Частично- поисковый | Исследова- тельский (твор- ческий) |
|
Классные и домашние Разного объема информации: а) теоретические; б) расчетные; в) экспериментальные |
Объем базового уровня | Объем программы | Объем сверх-программы |
ДИФФЕРЕНЦИАЦИЯ МЕТОДОВ И ФОРМ, ИСПОЛЬЗУЕМЫХ ПРИ ОБУЧЕНИИ МАТИМАТИКЕ.
В соответствии с уровнями дифференциации можно выделить следующие методы и формы, используемые при обучении математике. Эти данные представим в виде таблицы 1.4.2.
Таблица 1.4.2.
| Методы и формы обучения | Уровень дифференциации | ||
| Учащиеся с низкой успешностью обучения | Учащиеся со средней успешностью обучения | Учащиеся с высокой успешностью обучения | |
| 1.Самостоятельные работы с внепрограммным, дополнительным материалом | Экспресс-информация, сообщение | Реферат | Доклады |
| 2.Самостоятельные работы с учебником | Репродуктивные | Познавательно-творческие | Творческие |
| 3.Групповая работа (КСО) | Участник группы | Руководитель группы | |
| 4.Деловые игры | Участники игры | Исполнитель ролевой ситуации | Ведущие игры |
| 5.Внеклассные учебные занятия | Дополнительные занятия, консультации | Факультативы | |
| 6.Работа временных групп во внеурочное время | Группы по ликвидации пробелов | Группы для подготовки к олимпиадам | |
| 7.Программированный контроль | Ответы типа «правильно» - «неправильно» | Из 5 ответов – один правильный | Из 10 ответов – несколько правильных |
| 8.Работа в парах (консультанты) | Консультируемый | Консультант | |
| 9.Работа с обучающими программами | Подробная схема - программа | Средний уровень схематизации | Упрощенная схема - программа |
КЛАССИФИКАЦИЯ РАЗЛИЧНЫХ СПОСОБОВ ОРГАНИЗАЦИИ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ В УСЛОВИЯХ ДИФФЕРЕНЦИРОВАННОГО ОБУЧЕНИЯ
Способы организации учебной деятельности в условиях дифференцированного обучения можно разделить на три крупных блока:
1) фронтальная работа
2) групповая работа
3) индивидуальная работа.
Каждый из этих блоков делится в свою очередь на части по способу учебной деятельности каждого ученика. Представим это деление кратко в виде следующей таблицы:
Таблица 1.4.3.
Таблица № 6
Способы организации учебной деятельности.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Фронтальная работа Групповая работа Индивидуальная
Фронтальная работа Групповая работа Индивидуальная
![]()
|
1. Общеклассная ( Фронтальная ) с единым заданием. |
|
Групповая с единым заданием |
|
|
|
|
|
2. Фронтальная с дифференцирован- ным заданием. |
![]()
![]()
|
2. Групповая с дифференцированным заданием. |
![]()
![]()
![]() 3. Фронтально-вариантная.
3. Фронтально-вариантная.
Организация дифференцированного подхода на различных этапах урока.
Рассмотрим применение дифференцированного подхода на различных этапах урока.
ОРГАНИЗАЦИЯ ДИФФЕРЕНЦИРОВАННОГО ПОЛХОДА НА РАЗЛИЧНЫХ ЭТАПАХ УРОКА.
Рассмотрим применение дифференцированного подхода на различных этапах урока.
Первый этап. Введение нового материала.
Дифференцированный подход не есть что-то отдельно взятое, в процессе обучения он тесно связан с различными подходами. Так на основании статей Л.В. Виноградовой и В.А. Смирнова можно сделать вывод о том, что дифференцированное введение нового материала можно осуществить сочетанием двух подходов – дифференцированного и проблемного.
Было предложено осуществлять проблемный подход при изучении нового материала на трех уровнях.
На первом уровне ученики самостоятельно ведут поиск. Учитель указывает лишь результат, формулирует саму проблему.
На втором уровне, т.е. для другой группы учащихся, учитель указывает на проблему, но не сообщает конечного результата, ученики сами формулируют проблему
На третьем уровне учитель не указывает на проблему, а постепенно подводит учащихся к тому, что они самостоятельно усматривают ее.
Второй этап.
а) самостоятельные работы учащихся по изучению нового,
б) самостоятельные работы по применению изученной теории к решению задач.
В связи с этим заслуживает внимания работа С.В. Алексеева. Он предлагает разделить самостоятельные работы по степени помощи со стороны учителя ученикам (по наличию в них элементов помощи) на три группы (см. таблицу 1.4.4.).
Таблица 1.4.4.
|
Т Т Е О П Р Е О Н Н У Ь Ы В Е Л У И П Ч Ч О И И М Т В О Е А Щ Л Е И Я Т С С Я О |
Степень помощи | Элементы помощи |
| Первая группа | Задание, литература | |
|
Вторая группа а) или б) |
Задание, литература, план. Задание, литература, инструктаж |
|
| Третья группа | Задание, литература, план, инструктаж. |
Большинство методов дифференциации помощи со стороны учителя могут бить объединены в следующие основные группы:
1) указания типа задач, правила, на которые опирается данное упражнение;
2) дополнение к заданию в виде чертежа, схемы (и тут возможна дифференциация помощи: рисунок, чертеж без обозначений, чертеж с обозначениями и т.п.);
3) запись условия в виде таблицы, матрицы, графика;
4) указание алгоритма решения;
5) приведения аналогичной задачи, решенной ранее;
6) объяснение хода выполнения подобного задания;
7) предложение выполнить вспомогательное задание, наводящее на решение основной задачи;
8) наведение на поиск решения с помощью ассоциации;
9) указание причинно-следственных связей, необходимых для выполнения задания;
10) указания ответа, результата заранее;
11) расчленение сложной задачи на ряд элементарных;
12) постановка наводящих вопросов;
13) указание теорем, формул, на основании которых выполняется задание;
14) предупреждение о наиболее типичных ошибках, неправильных подходах и т. д. ;
15) указание ошибки в чертеже, в вычислениях, в постановке алгоритма работы, в установлении зависимости т. п. ;
16) использование вспомогательных дифференцированных крат (блоков информации по темам) различной степени помощи;
17) использование опорных конспектов;
18) использование рабочих тетрадей с печатной основой.
Третий этап. Работа с учебником.
При работе с учебником задания, предлагаемые учащимся, также могут быть дифференцированы. Например, одной группе учащихся предлагается прочитать теорему и выделить все шаги доказательства, другой – план доказательства; третьей группе предлагаются задания с пропусками и т.д.
Четвертый этап. Дифференцированный контроль подготовленности к уроку.
Н.В.Метельский предлагает на каждом уроке математики проводить фронтальный письменный опрос всех учащихся класса одновременно в двух вариантах на 10 минут. Он подчеркивает, что такие письменные опросы целесообразно проводить отдельно по трем основным компонентам содержания:
а) формулировка определений, теорем, правил и т. п. (типа математического диктанта);
б) доказательствам;
в) решению задач (выполнение упражнений)
Стимулируя подготовку всех учащихся к каждому уроку математики, систематически проводимые опросы класса будут предупреждать накопление пробелов в знаниях, приучать школьников к повседневной работе.
Пятый этап. Домашние задания.
М.М. Рассудовская предлагает составлять дифференцированные домашние задания, которые могли бы более полно использовать возможности учащихся и позволили бы организовать их проверку в классе. Принцип составления таких упражнений заключается в том, что первое упражнение предназначено для всего класса, а второе непосредственно связано с первым, но содержит по сравнению с первым некоторую дополнительную трудность.
Пример.
1. Выполните действия:
2. Используя предыдущий результат, вычислите устно:
Это пример дифференцированного домашнего задания. На самом деле они могут быть самыми различными по содержанию, в зависимости от той цели, с которой они делаются.
В заключение надо отметить, что выполнение задачи прочного усвоения школьного курса математики, который тесно связан с получением и осмысливанием большого объема учебной информации, невозможно без совместной согласованной деятельности учащихся по объединению и обобщению работы каждого. Коллективная деятельность при этом становится этапом завершения индивидуальной работы.
Следует подчеркнуть, что на каждом уроке учитель не имеет возможностей для полного и всестороннего учета индивидуальных особенностей всех учащихся.
Ориентация на обязательные результаты обучения постоянно поддерживает подготовку школьников на опорном уровне, это позволяет ученику при возможности и возникшем интересе перейти на более высокие уровни на любом этапе обучения. Кроме этого, так как каждый ученик работает на посильном для него уровне трудности, он лучше осознает свои ближайшие цели и задачи. Поэтому ведущим видом является уровневая дифференциация. Из анализа психолого-педагогической и методической литературы, а также изучения опыта работы учителей видно, что уровневую дифференциацию можно организовать в разнообразных формах, которые существенно зависят от индивидуального стиля работы учителя, от особенностей класса, от возраста учащихся и др. Уровневая дифференциация способствует более полному учету индивидуальных запросов учащихся, развитию их интересов и способностей. В условиях дифференцированного обучения ученик реализует право выбора предмета или уровня обучения в соответствии со своими склонностями.
1.5. Отбор учащихся для обучения в классах с углубленным изучением математики
Как показывает опыт, создание классов с общематематическим уклоном является не только дополнением к школам общематематического профиля, но и наиболее гибкой и экономичной формой углубленной математической подготовки, а также имеет ряд следующих преимуществ.
1) для создания класса с математическим уклоном бывает достаточно иметь одного высококвалифицированного учителя;
2) относительная легкость набора учащихся в 1-2 класса;
3) возможность почти в каждой школе «вырастить» будущих учащихся математического класса из состава учащихся 4-7 классов той же школы с помощью кружков, факультативных занятий и т.д.
Основными принципами построения программы курса математики для таких классов является:
1. Изучение математики в классах соответствующего профиля должно давать учащимся глубокие математические знания и широкое математическое развитие на базе основного курса математики.
2. Учащиеся – выпускники математических классов – должны обладать такими знаниями и умениями, которые полностью отвечали бы требованиям, предъявляемым к математической подготовке учащихся обычных школ, но вместе с тем были бы более глубокими и прочными.
Учащиеся должны научиться работать самостоятельно с учебной математической литературой и обладать к концу обучения устойчивым интересом к предмету естественно-математического цикла.
3. Возможное расширение программы должно быть органически связано с основным курсом и соответствовать имеющимся (возникающим) интересам учащихся и их познавательным интересам.
В процессе преподавания математики в этих классах открываются большие возможности в осуществлении оптимальной индивидуализации обучения, в использовании проблемного обучения, т.е. широкая возможность оптимальной активизации обучения. Организуя набор в такие классы целесообразно проводить общую для всех контрольную работу (тестовые задания) с последующим собеседованием с каждым из учащихся для выявления уровня развития и степени интереса к математике. Примерный образец такого теста мы приводим ниже.
Нередки случаи, когда уже в процессе работы в VIII классе выясняется, что у кого-то практически отсутствует элементарная логика, а кто-то, обладая одаренностью, совершенно не обучаем. Значит, необходимы формы отбора, которые позволили бы получить наиболее полное представление о том или ином школьнике.
Одна из оптимальных форм отбора учащихся в класс с углубленным изучением математики – задания в тестовой форме, нацеленные на диагностику умственного развития ребенка. Здесь предложены два из них.
Первое – это «тест интеллекта», основой которого является форма задания: испытуемые должны выявить некоторые закономерности. Этот тест должен дать представление о структуре интеллекта и способностях испытуемого.
Второе – это «тест достижений», где основой является не форма, а содержание задания и который позволяет выявить знания в предметной области (в нашем случае – в области математики).
Заметим, что нельзя идеализировать тестовую методику ни как средство диагностики, ни как средство контроля. В частности, отбор детей в специализированные классы может строиться на основе результатов тестирования, но с учетом мнения учителей, уровня мотивации ученика и других факторов. Тем не менее результаты теста могут быть показательными для проведения сравнительного анализа ряда качеств учащихся, что играет важную роль в процессе комплектования класса.
Приведем пример тестов, которые можно использовать в качестве одного из элементов конкурсного отбора семиклассников для их поступления в VIII класс с углубленным изучением математики. На выполнение каждого теста отводится 30 мин. Ответы к заданиям записываются в специальные бланки.
Бланки для записи ответов
к «тесту интеллекта» и к «тесту достижений»
| 1 | 1 | а); б); в); г) | ||
| 2 | 2 | -16; 0; 2; 4; 16 | ||
| 3 | 3 | 1); 2); 3); 4); 5) | ||
| 4 | 4; 8; 12; 16; 24 | 4 | ||
| 5 |
А) да/нет; Б) да/нет; В) да/нет; Г) да/нет |
5 | А); Б); В); Г) | |
| 6 | 6 | 3 см; 4 см; 5 см; 6 см; 9см | ||
| 7 | 7 | 1); 2); 3); | ||
| 8 | 8 |
у = х; у = х2; у = -х; у = |х| |
||
| 9 | 9 | А); Б); В); Г) | ||
| 10 | 10 |
Бланк заданий «теста интеллекта»
| № | Инструкция | Задание |
| 1 | Выберите из приведенного списка лишнее слово и запишите его |
Малиновый; желтый; сиреневый; лимонный |
| 2 | Запишите два слова, которые должны стоять на месте пропусков |
Лондон: Англия = = Париж : ... = = ... : Италия |
| 3 | Закончите данное предложение |
Из того, что Петя выше Толи, а Толя выше Оли, следует, что... |
|
|
Сколько треугольников изображено на рисунке? Правильный ответ обведите рамкой | |
| 5 | Обведите рамкой слово «да» если утверждение верно и слово «нет», если – неверно |
А) Если у человека высокая температура, то он болен. Б) Если человек болен, то у него высокая температура. В) Все звери живут в лесу. Г) Некоторые звери живут в лесу. |
| 6 | Запишите в порядке убывания следующие слова | кило, милли, деци, санти |
| 7 | Найдите два недостающих числа в указанной последовательности | 2; 5; 10; 17; ...; 37; 50; ...; 82; 101 |
|
|
Установите, какой элемент из II списка соответствует каждому элементу из I списка |
I список 1) 2) 3) 4) II список а) б) в) г) |
| 9 | Запишите грамматически правильную последовательность указанных слов | правила очень знает Вася хорошо |
| 10 | Запишите одно слово, которое является общим для всех четырех приведенных слов | хорда медиана высота радиус |
Бланк заданий «теста достижений»
| № | Инструкция | Задание |
| 1 |
Вычислите и запишите ответ |
а) |
| 2 |
Вычислите. Правильный ответ обведите рамкой |
7˚ + (-2)3 – 5 · (4,92 – 5,12) – (-1)4 + |-9| |
|
|
Установите, какой элемент из II списка соответствует каждому элементу из I списка |
I список: 1) углы 6 и 3 2) углы 2 и 3 1 2 а 3) углы 4 и 6 3 4 4) углы 7 и 8 5) углы 5 и 1 5 6 в 7 8 II список а) внутренние односторонние б) внутренние накрест лежащие в) соответственные г) смежные д) вертикальные |
| 4 |
Выпишите номера только тех формул, которые являются вернными |
1) а2 + в2 = (а – в) · (а + в) 2) х4 – 16 = (х – 2) · (х + 2) · (х2 + 4) 3) а2 + в2 + с2 = (а + в + с)2 4) с5 – 1 = (с – 1) · (с4 + с3 + с2 + с + 1) |
| 5 |
Запишите числа, которые должны стоять на месте пропусков |
А) 30% от 120 составляют ... Б) 12 составляет 60% от ... В) 15 составляет ...% от 20 Г) 16 больше, чем 8 на ...% |
|
|
Используя приведенный рисунок, найдите длину отрезка АD. Верный ответ обведите рамкой |
А | D 150° | В С 12см |
| 7 |
Установите, какой элемент из II cписка соответствует каждому элементу из I списка |
I список: 1) 2х = 0; 2) 0х = 0; 3) 0х = 2. II список: а) нет корней; б) один корень; в) бесконечно много корней. |
|
|
Подчеркните ту функцию которой соответствует указанный график |
у
1 -1 0 1 х |
|
|
Туристы прошли путь из пункта А в пункт F. На графике показана зависимость пройденного ими расстояния (s) от времени (t). Установите, истинно или ложно каждое из приведенных высказываний. Истинные высказывания отметьте знаком «+», а ложные – знаком «-». |
А) Протяженность маршрута составила 24 км; Б) Из А в F туристы шли без остановок; В) Участок CD был пройден ровно за 4 ч; Г) Участок AB был пройден со скоростью 8 км/ч S (км) F D 16 В С E
8
1 3 5 7 t (ч) |
| 10 |
Катер плывет по реке. Скорость течения реки равна х, а скорость катера в стоячей воде равна у. Какая из формул выражает время, которое затрачивает катер на то, чтобы спуститься вниз по течению на 30 км, а потом сразу вернуться обратно? (Выпишите номер подходящей формулы). |
1) 60 ; у-х 2) 30 + 30 ; у +х у – х 3) 30 + 30 ; х у 4) 30х + 30у |
Бланк правильных ответов
к «тесту интеллекта»
| № | Ответ к заданию |
| 1 | желтый |
| 2 | Франция, Рим |
| 3 | Петя выше Оли (Оля ниже Пети) |
|
|
4 8 12 16 24 |
| 5 | А) да / нет; Б) да/ нет ; В) да/ нет ; Г) да / нет; |
|
|
1) кило; 2) деци; 3) санти; 4) милли |
| 7 | 26 и 65 |
| 8 | 1) – в); 2) – г); 3) – а); 4) – б) |
| 9 | Вася очень хорошо знает правила |
| 10 | Отрезок |
Бланк правильных ответов
к «тесту достижений»
| № | Ответ к заданию |
| 1 |
а) 5 ; б) 1 ; в) 1 ; г) 3 ( или 1 1 , или 1,5) 6 6 6 2 2 |
|
|
-16; 0; 2 ; 4; 16 |
|
|
1) – б); 2) - д); 3) - а); 4) - г); 5) - в) |
| 4 | 2) и 4) |
| 5 | А) 36; Б) 20; В) 75; Г) 100 |
|
|
3 см; 4 см; 5 см; 6 см ; 9 см |
| 7 | 1) - б); 2) - в); 3) - а) |
| 8 |
у = х; у = х2; у = -х; у = |х| |
| 9 | А) +; Б) - ; В) - ; Г) + |
| 10 | 2) |
РОЛЬ ЗАДАЧ В ОБУЧЕНИИ МАТЕМАТИКЕ.
Важной целью задач является развитие мышления школьников. Задачи служат также основным дидактическим целям: формируют системы знаний, умений и навыков решения различных типов задач, творческое мышление учащихся; способствуют развитию интеллекта, мировоззрения, нравственных качеств, выполняют показательную роль в обучении. Задачи и процессы их решения являются основой реализации целей обучения, воспитания и развития.
Смысл задачи как средства обучения состоит в том, что только с ее помощью учебный материал, подлежит усвоению, может стать «предметом обучения лишь тогда, когда он принимает для учения вид определенной задачи, направляющей и стимулирующей учебную деятельность».
Задачи выступают так же как средство целенаправленного формирования математических способностей, познавательного интереса, самостоятельности, активности учащихся в обучении.
Вопрос о необходимости исследования самих задач как сложных объектов (а не только процессов их решения) в настоящее время четко ставится в психологических, дидактических и методических исследованиях. Так, например, У.Р.Рейтман отмечает: «… если мы попытаемся понять, как люди решают задачи какого-либо вида, нам необходимо иметь хорошее представление о структуре решаемой задачи».
Отсюда становится очевидным то, что эффективность процесса обучения решению задач повысится, если учитель и учащиеся будут иметь ясное представление о структуре задачи. В этом заключается суть задачи как предмета изучения.
Школьная математическая задача, как и любая задача, несет в себе две информации: субъективную и объективную.
Это положение позволило рассматривать задачу как сложный объект, имеющий внешнюю (информационную) и внутреннюю структуру. В связи с этим многие авторы рассматривают задачу как систему (системный подход) (Ю.М.Колягин, В.И.Крупич,Е.И.Машбиц и другие).
С точки зрения информационной структуры задачу можно рассматривать как замкнутую систему S = (A, С, R, D, В), где
А – условия (условие) задачи, то есть данные и отношения между ними;
В – требование задачи, то есть искомые (искомое) и отношения между ними;
С – базис решения задачи, то есть теоретическая и практическая основа, необходимая для обоснования решения;
D – способ, определяющий процесс решения задачи, то есть способ действия по преобразованию условий (условия) задачи для нахождения искомого;
R - основное отношение в системе отношений между данными и искомым.
Информационная структура задачи позволяет различать задачи по степени их психологической сложности (проблемности), как одного из основных компонентов трудности.
Трудность задачи есть психолого-дидактическая категория и представляет совокупность многих субъективных факторов, зависящих от особенностей личности, таких как степень ее новизны, интеллектуальные возможности учащегося, его потребности и интересы, опыт решения задач, уровень владения интеллектуальными и практическими умениями и др. Однако основными компонентами трудности задачи как объекта являются степень ее проблемности и сложности.
Сложность задачи является объективной характеристикой, не зависящей от субъекта. Она определяется внутренней структурой задачи.
Хотя выделен общий механизм построения внутренней структуры следующих задач школьного курса математики (текстовые задачи, дробно-рациональные уравнения, геометрические задачи на вычисление) единого подхода к пониманию внутренней структуры задачи не существует.
Например, А.М.Сохор при выявлении внутренней структуры задачи опирается на характер внутренних отношений (связей, зависимостей) между данными и искомыми величинами.
Е.И.Лященко, Г.Н.Васильева выявляют структуру задачи, исходя из структуры ее решения.
Школьная математическая задача содержит некоторое множество отношений. Например, это отношения между данными, между искомыми, то есть между условием и требованием задачи. В этом множестве отношений на основе обобщения можно выделить главное, ведущее отношение, которое принято называть основным. Основное отношение в общем случае выражает функциональную зависимость между величинами, входящими в условие и требование задачи, и реализовано на предметной области задачи.
Выявление основного отношения в процессе анализа задачи является необходимым условием построения методики обучения решению задач на основе реализации системного типа ориентировки учащихся в этом процессе, а также выявления внутренней структуры задачи, ее элементов.
СИСТЕМНЫЙ ПОДХОД К ОБЪЕКТУ ИССЛЕДОВАНИЯ.
Характерной чертой современной науки является направленность научного познания на управление в природе и обществе. В связи с этим значительное место в научных исследованиях стала занимать общенаучная методология системных исследований.
Обобщенной научной формой ее выражения является системный подход к объекту исследования. Основой этого подхода является философский принцип системности, сущность которого состоит в том, что объект исследования рассматривается как нечто целое, имеющее определенную структуру.
Основными понятиями системного подхода являются система, структура и элемент.
Система – совокупность элементов, находящихся в отношениях и связях между собой и образующих определенную целостность, единство.
Структура – строение и внутренняя форма организации системы, выступающая как единство устойчивых взаимосвязей между ее элементами, а также законов данных взаимосвязей.
Под элементом понимают объект, входящих в состав определенной системы и рассматриваемый в ее пределах как неделимый.
Основными принципами системного подхода являются принцип целостности, принцип сложности и принцип организованности.
Под целостностью понимается такая характеристика объекта, которая позволяет отразить объект в единстве его элементов и связей. Целое выступает как совокупность связей и отношений между его частями, обладающее качественно новыми свойствами.
Целостность объекта проявляется также в сложности и иерархичности строения объекта, в наличии нескольких уровней его организации. Если отсутствует хотя бы один из уровней его организованности, то целостность разрушается.
Иерархичность системы означает, что каждая ее подсистема может рассматриваться как система, а сама исследуемая система представляет собой лишь одну из подсистем более широкой системы (количество элементов, связей и др.).
Отметим, что деятельностный подход к процессу обучения при исследовании объекта также опирается на принципы системного подхода.
Действительно, если рассмотреть структуру человеческой деятельности, состоящую из следующих взаимопереходящих друг в друга элементов: деятельность, действие, операция и потребность, мотив, цель; с точки зрения системного подхода, то здесь действуют все основные принципы системного подхода: целостность, сложность и иерархичность (организованность).
Основные принципы системного подхода находят непосредственную реализацию в процессе анализа объективной информации, определяющей внутреннюю структуру и сложность задачи.
Глава 2. Методические основы уровневой дифференциации.
В данной главе мы более подробно рассмотрим такие способы организации учебной деятельности в условиях дифференцированного обучения как фронтальная, групповая и индивидуальная работа, и их практическую реализацию. Глава содержит также ряд практических задач различной степени сложности.
Формирование математического мышления предполагает целенаправленное развитие на предмете математики всех качеств, присущих естественнонаучному мышлению, комплекса мыслительных умений в органическом единстве с формами проявления мышления.
В процессе обучения математике, естественно уделять особое внимание развитию у учащихся качеств мышления, специфичных для мышления математического. Органическое сочетание и повышенная активность разнообразных компонентов мышления вообще и различных его качеств проявляются в особых способностях человека, дающих ему возможность успешно осуществлять деятельность творческого характера в разнообразных областях науки. Математические способности – это определенная совокупность некоторых качеств творческой личности, сформированных и применяемых в процессе математической деятельности.
Совокупность способностей, присущих творческой личности, реализуемых в процессе мышления, называют творческим мышлением.
Факторы творческого развития выражаются в следующих принципах:
1) творческие потенциалы заложены в каждом ребенке;
2) развитие творческого стиля мышления происходит только в творческой деятельности;
3) формирование творческой инициативности зависит от условий социальной среды.
Итак, можно сделать следующий вывод: творчество – природная функция мозга, творчество зависит от условий обучения.
Создание этих условий одно из важнейших задач педагога. Одним из них является выбор формы организации работы и типа урока по технологии - творческого развития.
1-ый тип урока – урок анализа домашнего задания
2-ой тип урока – урок выравнивания знаний.
Цель урока - Создать для всех учащихся равные стартовые условия до начала изучения нового учебного материала, т.е. выравнивание знаний по усвоенному ранее материалу.
3-ий тип урока – урок постановки учебной задачи.
Цель урока – научить учащихся целеобразованию, формулировать учебные задачи на первом этапе урока.
При традиционном обучении учебные цели ставит сам учитель, а учащиеся должны их принять к исполнению. Технология урока творческого развития предполагает создание ситуации целеобразования, где возникает процесс порождения новых целей в учебной деятельности, что является одним из важных проявлений творческого мышления.
Целеобразование может быть непроизвольным и произвольным, когда цель возникает в результате специального намерения и планирования.
Существуют различные механизмы целеобразования:
1) внешние требования учителя превращаются в индивидуальную цель;
2) превращение мотивов в цели при их осознании;
3)преобразование неосознанных предвидений в цели и т.д.
4-й тип урока – урок решения учебной задачи (УЗ).
Цель урока – Научить учащихся теоретическому анализу учебного материала, развивать и формировать диалектико-логический, творческий способ мышления.
Процесс решения учебной задачи самый ответственный этап урока, где формируются интеллектуальные способности, творческое мышление, способность к самодвижению
Учебная задача только тогда является действительно «учебной», если она квалифицированно расчленена на дискретные части, т.е. на элементарные задания, раскрывающие УЗ только с какой-то одной стороны. При этом каждое задание у учащихся вызывает проблемную ситуацию.
Максимальные результаты в обучении и воспитании учащихся возможны только при комплексном и умелом использовании всех научных открытий и рекомендаций. Однако для этого нужен совершенно другой тип специалистов, работающих на уровне педагогической акмеологии, т.е. ученые и учителя, достигшие высшей степени профессионализма. К сожалению, фактическое положение таково, что одни знают, что такое развивающее обучение, другие – что такое проблемное обучение, третьи – еще что-то, но трудно найти специалистов, которые в равной мере умели бы продуктивно использовать результаты разных научных школ.
5-й тип урока – урок формирования общего способа.
Цель урока – научить учащихся выделению учебных (умственных) действий и формулировать на их основе общие способы в процессе решения учебной задачи.
6-й тип урока – урок моделирования содержания материала или способов решения.
Цель урока – научить учащихся действиям моделирования усвоенного учебного материала в графической, знаковой, символической или другой форме.
Учебное моделирование – это процесс чистого творчества, великолепное средство познания и содержательного обобщения знаний и способов действий. Учебная модель является результатом творческого анализа научного понятия и условием формирования устойчивой мотивации учения.
Урок моделирования может проходить в двух формах: как процесс (фиксированный в наглядно-логической форме), как результативное средство (модель фиксирования в конце урока в результате специального задания).
7-й тип урока – урок самоконтроля.
Цель урока – научить учащихся осуществлять контроль над своими учебными действиями.
Самоконтроль – основное нравственное действие человека связанное с развитостью его волевой сферы. Самоконтроль осуществляется на основе личностно значимых мотивов и установок, что ведет к рациональной рефлексии и оценке учащимися своих собственных учебных действий. Самоконтроль учащихся предполагает сличение, анализ и коррекцию отношений между целями, средствами и результатами.
Различают следующие основные виды:
1) итоговый контроль (по результату);
2) процессуальный;
3) прогнозирующий;
8-й тип урока – урок самооценки.
Цель урока - научить учащихся осознавать степень усвоения учебного материала и адекватно оценивать свои знания.
Школьная самооценка - это оценка учеником самого себя, своих знаний, возможностей, качеств и занимаемого места среди одноклассников. Учебная самооценка является важным регулятором поведения школьника и относится к главному фактору формирования личности.
В самооценке необходимо выделять ее адекватность, надежность и полноту.
9-й тип урока – урок учебной деятельности (творческого развития).
Цель урока - научить детей работать в ситуации целостной учебной деятельности, где в свернутой, обобщенной, сокращенной форме одновременно присутствуют все типы уроков как структурные, естественные компоненты типичного (обычного) урока творческого развития.
Обычный, «классический» тип урока творческого развития в себя включает все «чистые типы» уроков.
10-й тип урока – урок усвоения групповых форм учебной деятельности.
Цель урока - научить учащихся работать в группах, знания добывать совместными усилиями.
2.1. Фронтальная работа.
Фронтальная работа может осуществляться в нескольких видах:
- подача нового материала;
- устные упражнения – как средство для повторения и моделирования проблемы;
- работа с классом.
Значение этого метода достаточно велико, но для повышения эффективности обучения необходимо комбинировать его с другими формами.
Задания для фронтальной работы могут быть направлены на активизацию
1) процесса памяти;
2) процесса логического мышления на базе имеющихся навыков и знаний;
3) творческой деятельности и поиска новых знаний.
Рассмотрим несколько примеров реализации дифференцированного подхода во фронтальной работе
Пример 1. Для примера выберем тему «Прогрессии»
Покажем план урока подачи нового материала в классах различного типа и уровня развития.
1. Класс сильный, думающий, увлеченный математикой.
Сама математика как предмет держат его внимание. Потому, с одной стороны, в таком классе легко работать, но с другой стороны, есть и сложности. Особенно если тема простая, а рассматриваемая нами тема «Прогрессии» не содержит сложного материала.
Если идти по пути построения урока, достойного развития детей, то можно начать изучение двух тем параллельно. Например, дается определение арифметической прогрессии, приводятся примеры, и тут же рядом записывается определение геометрической прогрессии, составленное по аналогии самими учащимися. Действительно, если есть арифметическая прогрессия, то, наверное, существует и геометрическая.
Затем встает вопрос о формуле любого числа. Здесь сами ребята догадаются о ее структуре и докажут справедливость. Учителю придется подсказать лишь каким методом это сделать. Уместен будет разговор о методе математической индукции, хотя в качестве информации.
Последними можно рассмотреть характеристические свойства.
При всем этом нельзя забывать, что даже этот круг учеников нуждается в отработке элементарных операций. Поэтому далее целесообразно включить устную работу (10-15 мин.), направленную на отработку специальных умений по этой теме. Затем решить по одной задаче на характеристическое свойство каждой из прогрессий.
Закончить урок можно решением таких задач:
Задача 1. Выписаны 2 арифметические прогрессии. Если из каждого члена первой прогрессии вычесть соответственно член второй прогрессии, то получится ли снова арифметическая прогрессия?
Решение:
Ответ: да.
Задача 2. Могут ли три последовательных члена арифметической прогрессии вместе с тем быть и тремя последовательными членами геометрической прогрессии? (прогрессии с неравными членами).
Решение: Пусть числа а, в, с, образуют арифметическую прогрессию и геометрическую одновременно, тогда:
Ответ: нет.
Задача 3. В двух трехчленных прогрессиях (арифметической и геометрической с положительными членами) одинаковы оба первых и оба последних члена. В какой из них сумма членов больше?
Ответ: в арифметической.
Однако вместо этих задач можно сделать экскурс в историю. Рассказать о том, что примеры отдельных арифметических и геометрических прогрессий можно встретить еще в древне-вавилонских и египетских надписях (500-400 лет до нашей эры), что в Древней Греции были известны такие суммы:
А знаменитая задача о награде за изобретение шахматы впервые встречается у хорезмского математика Аль-Бируни
Можно упомянуть и о бесконечных рядах и их применении. Впечатляет и способ вычисления суммы бесконечного ряда
2. Класс шумный, думающий, заинтересованный предметом, но с недостаточно развитой самостоятельностью действий.
В этом случае работа будет носить фронтально-индивидуальный характер. Учащиеся, отвечающие вышеизложенной характеристике, любят учиться, но испытывают тягу к получению быстрых результатов. Однако с большим интересом воспринимают информацию о самих себе: о своей памяти, внимании, работоспособности. Учитель должен завладеть вниманием учащихся и удержать его до конца урока. Класс с готовностью выполняет четкие указания учителя и этот момент надо непременно использовать. Но необходимо не трафаретное начало. Поэтому учащихся можно сразу озадачить вопросами: какие анализаторы человек использует при восприятии информации? Дальше можно сказать, что основными являются анализаторы запаха, вкуса, осязания, слуха. Для рационального восприятия необходимо знать свой доминирующий анализатор, обычно зрение или слух. Именно его следует использовать в первую очередь. Для выявления учеников предлагаются задания следующего типа. На доске записаны числа 6,8,10,12,14,16,18,20;-12; -9; -6; -3; 0; 3; 6; 9; 12.
Учащиеся после минутного рассмотрения должны воспроизвести запись в тетрадях, что удается не каждому. Далее им предлагается ряд равенств, для запоминания которых включается не только зрительная, но и логическая память:
Затем делается акцент на слуховую память: медленно читается определение, которое необходимо записать после прослушивания.
«Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом, называется арифметической прогрессией». После паузы читается определение еще раз и все проверяют запись.
После этого можно сделать общий вывод принципов рационального восприятия информации:
1. Постановка цели: что люди мыслят под этим понятием, хочу про него знать все.
2. Использование основного анализатора.
3. Интерес.
Далее дети читают в своем темпе параграф по теме.
Завершает урок ряд задач из учебника или подобранных учителем.
Пример 2. Устные упражнения.
Устные упражнения заслуживают особого внимания. Они эффективны кажущейся легкостью, эмоциональностью, действуют на учащихся мобилизующе, способствуют развитию внимания и памяти, но требуют от школьников большого умственного напряжения, поэтому могут быстро их утомить.
На ряду с чисто устными практикуются также полуустные (зрительно-слуховые), когда задания записаны на доске или проецируется на экран. Некоторые мы рассматривали в предыдущем примере, когда с их помощью вводился новый материал.
Устные упражнения успешно применяются и при повторении. Например, при подготовке к контрольной работе в 8 классе по теме «арифметический квадратный корень» можно предложить следующую систему устных упражнений:
- в начале урока:
1) Известно, что площадь квадрата составляет а2; 36; 900 кв.ед. Чему равна его сторона?
Запись на доске:
2) Сравнить значения выражений:
3) Упростить выражения:
4) Назвать область определения:
5) Решить уравнения (назвать его корни):
- после блока повторения – построение графиков:
1) указать ход построение графиков:
Приведем так же пример обобщающего повторения. В начале 9 класса необходимо восстановить в памяти учащихся все о квадратном трехчлене и квадратных уравнениях с помощью упражнений:
1. Указать общий вид квадратных уравнений, корни которых равны по величине, но противоположны по знаку:
2. При каком значении «а» один из корней уравнения
3. Выразите зависимость между коэффициентами уравнения
4. Составьте такое уравнение, чтобы сразу было видно, что оно имеет три корня 0; 2; 5.( Ответ:
Фронтальную работу можно использовать так же при текущем контроле знаний и умений учащихся. Например, в форме математического диктанта, при чем задания можно давать повариантно: первый вариант доказывает свойство умножения степеней с одинаковыми основаниями, второй – свойство возведения степени в степень; в качестве второго задания даются не сложные примеры на вычисление и т.п.
2.2 Групповая работа.
Для того, чтобы обучение проявляло развивающий эффект, необходимо соблюдать универсальное условие: развиваемый субъект должен быть включен в активную деятельность и общение. Это условие вытекает из того, что ученик в учебном процессе не только объект, но и субъект процесса собственного учения.
Формирование творческой активности – высшая цель активизации, но нельзя игнорировать более низкие ее ступени. К содержательной стороне активизации относятся составление и предъявление заданий, активизирующих учебно-познавательный процесс. Другой ее стороной является организация активизированной учебной работы.
Групповая работа – одна из форм активизации учащихся. По определению Х.И.Лийметса под групповой работой понимают такое построение работы, при которой класс делится на группы по 3-8 человек (чаще по четыре человека) с целью выполнения той или иной учебной задачи.
Групповая работа так же представляет много возможностей для индивидуализации, особенно, если группы составлены из схожих по какому-либо признаку учащихся, причем тогда для каждой группы подбираются специальные задания.
В малой группе учащийся находится в более благоприятных условиях, чем при фронтальной работе. Группы могут быть сформированы как учителем (на основании уровня знаний и/или умственных способностей), так и по пожеланию учащихся.
Групповая работа достаточно эффективна, однако следует следить за тем, чтобы более сильные и старательные не заглушали инициативу более слабых и пассивных. Целесообразно проводить работу также с относительно стабильными группами, что позволяет оперативно распределять задания различной степени сложности, причем по результатам обучения возможен переход из одной группы в другую.
И так групповая учебная деятельность – это организованная система активности взаимодействующих учащихся, направленная на целенаправленное решение поставленной учебной задачи.
Основными показателями являются отношение учашихся к совместному действию. Это отношение выявляется
1) по характеру деятельности группы при выполнении задания;
2) по используемым средствам фиксации совместного действия (моделирование, выработка способа, формулировка выводов и т.д.)
3) по характеру общения членов группы.
При учебной кооперации учащиеся выполняют общую работу, осуществляя обмен операциями и мнениями. В это процессе наступают понимание каждым участником своей зависимости от действий другого и ответственности.
Рассмотрим систему задач разной тематики для возможного решения в группах. Задачи подобраны по следующему принципу: по каждой теме предлагается по две задачи, причем одно из них является более сложной в смысле выявления способа решения или выделения основных отношений и связей и требует творческого подхода к решению.
1. Упростить выражение
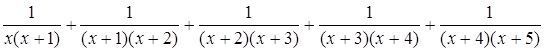
Решение.
Тактически нецелесообразно складывать сразу все дроби.
Сложим первые две: 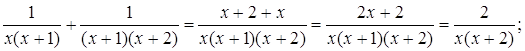
Прибавим третью: 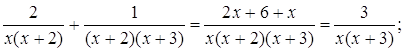
Затем четвертую : 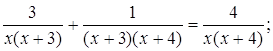 и пятую:
и пятую: 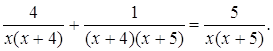
Можно предложить и другой способ решения.
Легко проверить, что
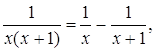 причем аналогичные равенства
справедливы и для других дробей. Заменив каждую дробь. Входящую в выражение на
соответствующую разность получим:
причем аналогичные равенства
справедливы и для других дробей. Заменив каждую дробь. Входящую в выражение на
соответствующую разность получим:
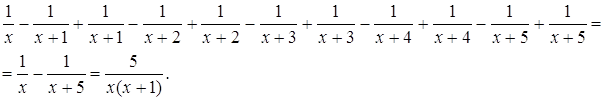
Ответ: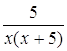 .
.
2. Докажем равенство
![]()
Решение.
Преобразуем левую часть данного равенства:
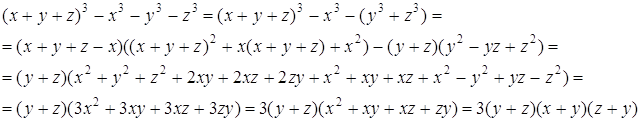
Поменяв местами множители, получим выражение, стоящее в правой части.
3.Решить уравнение.
![]()
Решение.
Вместо стандартного освобождения от знаменателя, приведения подобных слагаемых и решение полученного квадратного уравнения, объединим дроби в пары и произведем действия внутри пар:
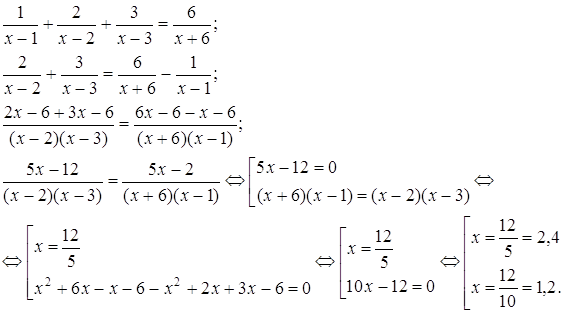
Ответ: ![]()
4. Решить уравнение:
![]() .
.
Решение.
Замена ![]() , тогда
, тогда ![]() , а
, а ![]() . Подставляем полученные
выражения в исходное уравнение, имеем:
. Подставляем полученные
выражения в исходное уравнение, имеем:
![]() ;
;
![]() ;
; ![]() .
.
![]() не удовлетворяет условию
не удовлетворяет условию ![]() .
.
Возвращаемся к ![]() :
:
![]() ;
;
![]() .
.
Ответ: ![]()
5. Решить систему уравнений:
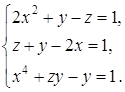
Решение.
Выразим
![]() , из второго уравнения
, из второго уравнения ![]() :
:
![]() и
подставляем в первое и третье уравнения системы:
и
подставляем в первое и третье уравнения системы:
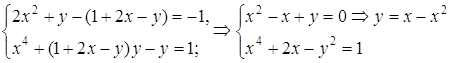
Выразив
![]() через
через ![]() и подставив во второе
уравнение, получим:
и подставив во второе
уравнение, получим:
![]()
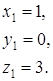
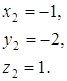
Ответ:
![]() ,
,![]() .
.
5. Решить систему уравнений:
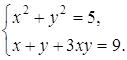
Решение.
Предложенная система
является симметричной: замена ![]() на
на ![]() , а
, а ![]() на
на ![]() не меняет каждого из
уравнений системы.
не меняет каждого из
уравнений системы.
Используем замену
переменных: ![]() .
.
Поскольку ![]() , относительно
, относительно ![]() и
и ![]() получим следующую систему:
получим следующую систему:
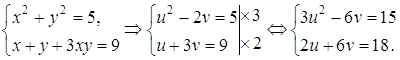
![]()
Для ![]() и
и ![]() соответственно будем иметь
две системы:
соответственно будем иметь
две системы:
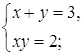
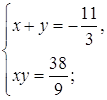 Вторая система не имеет
действительных корней, первая имеет два решения: (1;2); (2;1).
Вторая система не имеет
действительных корней, первая имеет два решения: (1;2); (2;1).
Ответ: (1;2); (2;1).
7. Решить неравенство:
![]()
Решение.
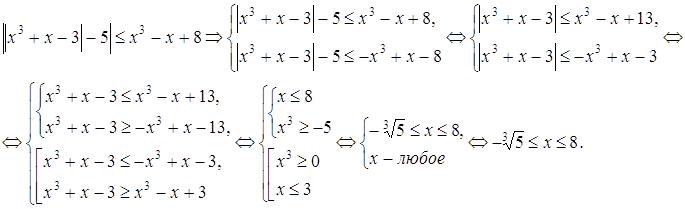
Ответ:![]() .
.
8. Решить неравенство:
![]()
Решение.

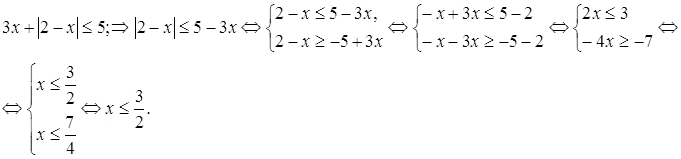
Ответ:![]() .
.
Стандартная схема решения текстовых задач состоит из трех этапов:
1. Выбор неизвестных.
2. Составление уравнений (неравенств).
3. Нахождение нужного неизвестного или нужной комбинации неизвестных.
Рассмотрим несколько примеров.
9. От пристани А одновременно отправились вниз по течению катер и плот. Катер спустился вниз по течению на 96км, затем повернулся обратно и вернулся в А через 14ч. Найти скорость катера в стоячей воде и скорость течения, если известно, что катер встретил плот на обратном пути на расстоянии 24км от А.
Решение.
I способ (алгебраический).
1)
Пусть ![]() (км/ч) скорость катера в
стоячей воде, у (км/ч) – скорость течения.
(км/ч) скорость катера в
стоячей воде, у (км/ч) – скорость течения.
2)
Составим уравнения. Поскольку скорость катера при движении по течению ![]() , а против течения
, а против течения ![]() , то на основании того, что
сказано во второй фразе условия, получим:
, то на основании того, что
сказано во второй фразе условия, получим:![]() или
или
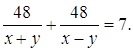
Вторая часть последней фразы дает нам 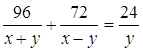 (плот прошел до встречи
24км, катер 96 – 24 =72км на обратном пути).
(плот прошел до встречи
24км, катер 96 – 24 =72км на обратном пути).
Таким образом, имеем систему уравнений
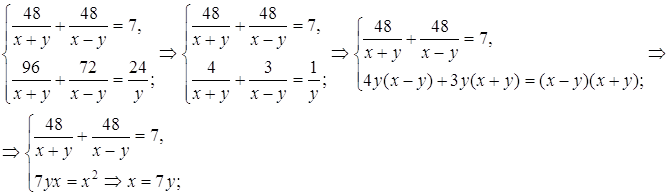
Подставляем
![]() в I уравнение
системы
в I уравнение
системы
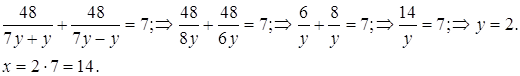
Ответ: скорость катера в стоячей воде 14км/ч, скорость течения 2км/ч.
II способ (арифметический).
Итак, если катер удаляется от плота или приближается к нему, то его скорость относительно плота равна скорости катера в стоячей воде, меняется лишь направление этой скорости. Следовательно, катер удаляется от плота за то же время, что и приближается к нему, т.е. путь в 96км пройден за то же время, что и путь 72км (против течения).
96 : 72 = 4 : 3- отношение скорости катера по течению к скорости катера против течения.
Весь путь занял 14ч. Разделим число 14 на части пропорционально 3:4 :
![]() катер
шел по течению;
катер
шел по течению;
![]() катер
шел против течения.
катер
шел против течения.
96 : 6 =16 (км/ч) – скорость по течению;
96 : 8 =12 (км/ч) – скорость против течения;
![]() -
скорость течения;
-
скорость течения;
![]() -
собственная скорость катера.
-
собственная скорость катера.
Ответ: 2км/ч; 14км/ч.
Как видно из решения задачи 9 «арифметический» способ решения зачастую удобнее, так как для него характерна достаточность знаний и умений, которыми располагает учащийся, окончивший начальную школу плюс, конечно развитый логический аппарат.
10. Лошадь съедает копну сена за 2 дня, корова может съесть такую же копну за 3 суток, овца за 6 суток. За какое время они съедят эту копну вместе?
Решение.
Задача
может даваться с 6 класса. Итак, если лошадь съедает копну сена за 2 дня, то за
один день она съест ![]() часть копны,
аналогично корова
часть копны,
аналогично корова ![]() часть копны, а
овца
часть копны, а
овца ![]() часть копны.
часть копны.
За
один день вместе они съедают ![]() копны
сена, т.е. всю.
копны
сена, т.е. всю.
Ответ: 1 день.
Функции
![]()
Наибольшее
значение ![]() при
при ![]() . Возвращаясь к
. Возвращаясь к ![]() , получим, что
, получим, что ![]() при
при ![]()
Ответ:
наибольшее значение ![]() .
.
Почти вся теория квадратного трехчлена основывается на приеме, называемом «выделение полного квадрата»:
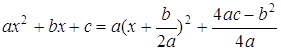
![]() -
дискриминант квадратного уравнения.
-
дискриминант квадратного уравнения.
Если
![]() , то уравнение имеет два
корня,
, то уравнение имеет два
корня,
![]() ,то уравнение имеет1 корень
(2 совпадающих);
,то уравнение имеет1 корень
(2 совпадающих);
![]() , уравнение не имеет действительных
корней.
, уравнение не имеет действительных
корней.
11.
Доказать, что при любом ![]() уравнение
уравнение
![]() имеет
решения.
имеет
решения.
Процесс нахождения дискриминанта и доказательства, что он положителен достаточно трудоемкий, поэтому попробуем другой метод решения.
Пусть
![]() .
.
![]() при любом
при любом ![]() .
.
Т.о.
уравнение всегда имеет решение, причем если ![]() ,
то уравнение имеет два корня; при этом всегда имеется корень, удовлетворяющий
неравенству
,
то уравнение имеет два корня; при этом всегда имеется корень, удовлетворяющий
неравенству ![]() .
.
12.
Пусть ![]() и
и ![]() корни уравнения
корни уравнения ![]() . Выразить
. Выразить ![]() через
через ![]() и
и ![]() .
.
Решение.
Необходимо
выразить ![]() через
через ![]() и
и ![]() :
:
![]()
По
теореме Виета ![]()
тогда
![]()
Ответ: ![]() .
.
13.
Определить все значения параметра ![]() , при
которых уравнение
, при
которых уравнение ![]() имеет 1 корень.
имеет 1 корень.
Решение.
В
условие не сказано, что рассматривается квадратное уравнение, поэтому
рассмотрим случай ![]()
Остальные
значения параметра получим из уравнения ![]() .
.
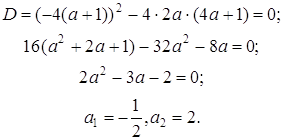
Ответ:
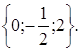
Простейший прием нахождения наибольших значений, основанный на свойствах квадратичных функций состоит в том, что исследуемая функция при помощи преобразований или замены переменной приводится к квадратичной, после чего выделяется полный квадрат.
14.Найти наибольшее значение функции
![]()
Решение.
Положим
![]() , тогда
, тогда ![]() Отсюда
Отсюда ![]() Итак, после замены получим,
что надо найти наибольшее значение
Итак, после замены получим,
что надо найти наибольшее значение
15.Найти
наибольшее и наименьшее значения функции 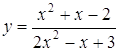 .
.
Решение.
Рассмотрим
данное неравенство как уравнение с неизвестным ![]() и
параметром
и
параметром ![]() .
.
После преобразований получим
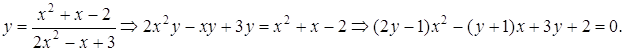 Для того, чтобы уравнение имело решение
необходимо и достаточно, чтобы
Для того, чтобы уравнение имело решение
необходимо и достаточно, чтобы
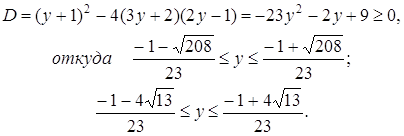
Отсюда
наименьшее значение функции 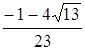 ,
наибольшее
,
наибольшее 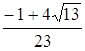 .
.
Ответ: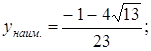
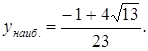
Как
видно из решений последних задач на нахождение наибольшего и наименьшего
значений иногда удобнее рассматривать функцию ![]() как
уравнение с неизвестным
как
уравнение с неизвестным ![]() , в
котором необходимо установить при каких
, в
котором необходимо установить при каких ![]() это
уравнение имеет решение. Рассмотрим еще один пример, в котором работает эта
идея с небольшими вариациями.
это
уравнение имеет решение. Рассмотрим еще один пример, в котором работает эта
идея с небольшими вариациями.
16.
Найти наибольшее и наименьшее значение выражения ![]() ,
если
,
если
![]() .
.
Решение.
Положим
![]() . Подставим полученное выражение
в (1):
. Подставим полученное выражение
в (1):
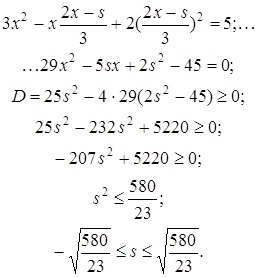
Ответ:
наибольшее значение выражения ![]() равно
равно ![]()
![]() ;
наименьшее -
;
наименьшее - 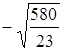 .
.
Рассмотрим один из самых универсальных методов доказательства – методом математической индукции.
17.
Доказать, что при любом натуральном ![]() число
число ![]()
![]() делится
на 7.
делится
на 7.
Решение.
Обозначим
![]() .
.
1)
При ![]()
![]() - делится на 7.
- делится на 7.
2)
Пусть ![]() делится
на 7.
делится
на 7.
Имеем 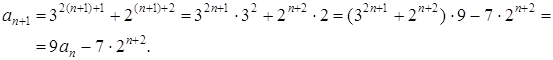
Последнее число делится на 7, т.к. представляет собой разность двух целых чисел, которые делятся на 7, ч.т.д.
17. Доказать тождество:
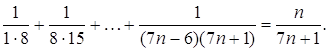
Решение.
1)При
![]()
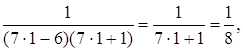 равенство выполняется.
равенство выполняется.
2)Предположим,
что равенство выполняется при ![]()
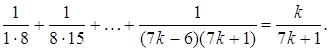
При
![]() имеем:
имеем:
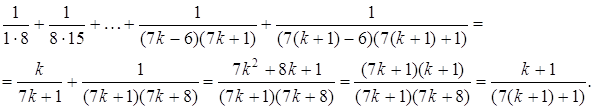
ч.т.д.
18. Выполнить следующие действия:
а)
![]() ; б)
; б) ![]() ; в)
; в)![]()
Решение.
а)
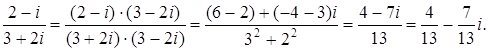
б)
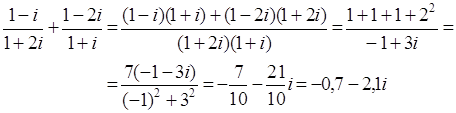
в)
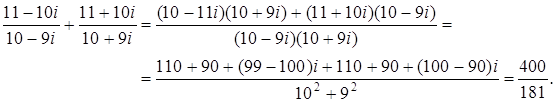
Ответ: а)![]() ; б)
; б)![]() в)
в)![]()
19. Решить уравнения:
а)
![]() ;
;
б)
![]()
Решение.
а)
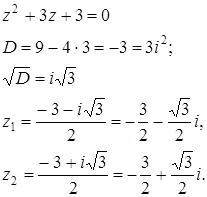
б)
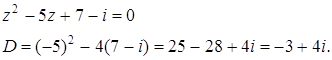
Чтобы
найти ![]() не будем переходить к
тригонометрической форме (но и этот путь верный). Итак, надо найти числа
не будем переходить к
тригонометрической форме (но и этот путь верный). Итак, надо найти числа ![]() и
и ![]() такие что,
такие что, 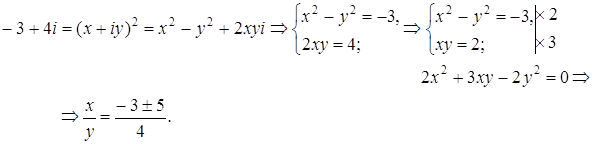
Достаточно
найти одно решение ![]()
Т.о.
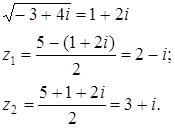
Ответ: а)![]() б)
б)![]() .
.
2.3. Индивидуальная работа учащихся.
Поскольку внеклассная индивидуализация осуществляется в основном в форме самостоятельной работы, следует, естественно, учитывать требования, исходящие из методики самостоятельной работы.
Самостоятельная работа учащихся – это такой способ учебной работы, где 1) учащимся предлагаются учебные задания и руководства для их выполнения; 2) работа проводится без непосредственного участия учителя, но под его руководством; 3) выполнение работы требует от учащегося умственного напряжения.
С точки зрения организационных основ самостоятельную работу можно разделить на: 1) самостоятельную работу в школе и 2) самостоятельную работу, выполняемую за пределами школы, в т. ч. и дома. Самостоятельная работа в школе может проводиться в рамках урока, зачета, семинара, практического занятия и т. д. На основе другого логического членения можно выделить еще два вида самостоятельной работы: 1) индивидуальную и 2) групповую.
В ходе самостоятельной работы каждый ученик получает конкретное задание, которое предполагает и выполнение определенной письменной работы. В этом случае можно проверить степень участия ученика в выполнении этого задания. Самостоятельная работа позволяет работать и в индивидуальном темпе и стиле.
Учебные задания для самостоятельной работы.
Учебные задания для самостоятельной работы весьма разнообразны. Их можно в основном делить на следующих 4 логических основаниях: 1) по методу самостоятельной работы учащихся (например, наблюдения, упражнения, работа с текстом учебника); 2) по звеньям учебного процесса (задания на восприятие, систематизацию, закрепление и повторение учебного материала); 3) по характеру познавательной деятельности учащегося (репродуцирующие и творческие задания); 4) по характеру руководства (подробное или менее подробное инструктирование).
Выделяют 3 основных вида основной работы:
А. Учебные задания, опосредующие учебную информацию. В учебном задании соответствующая информация дана непосредственно или же задание указывает на источник, откуда можно получить необходимую информацию. Этот вид задания заменяет устное изложение учителя и предназначен в основном для первоначального восприятия учебного материла.
Б. Учебные задания, направляющие работу ученика с учебным материалом. Эти задания ориентируют ученика на осмысление и систематизацию учебного материала, а также на самоконтроль; наводят на сравнение, выводы, обобщения.
В. Учебные задания, требующие от ученика творческой деятельности. Эти задания направляют ученика к решению проблем, к самостоятельному сбору материала, к составлению заданий.
Рабочее руководство к индивидуализированной самостоятельной работе.
Рабочее руководство к индивидуализированной самостоятельной работе представляет собой, в принципе, такое же рабочее руководство, которое используется при обычной самостоятельной работе. Поэтому по отношению к нему действуют точно такие же требования. Эти руководства различаются тем, что в пределах класса не ограничиваются только одним-единственным рабочим руководством, а составляют его варианты, где учитываются индивидуальные особенности учащихся с помощью индивидуализированных заданий.
Варианты рабочего руководства могут отличать друг от друга или частично, или полностью. Выбор варианта зависит от того, в какой мере желают индивидуализировать учебную работу.
Среди вариантов, использованных в наших экспериментах, можно выделить следующие типы рабочих руководств:
1 тип.1. Общие задания.
2. Дополнительные задания более быстрым и сильным ученикам.
2 тип.1. Общее задание.
2. Разветвленные задания: а) более легкий вариант, б) средний вариант, в) более трудный вариант.
3 тип. Разветвленные задания: а) более легкий вариант, б) средний вариант, в) более трудный вариант.
4 тип. 1. Разветвленные задания: а) более легкий вариант, б) средний вариант, в) более трудный вариант.
2. Общие задания.
АЛГЕБРА IX КЛАСС
I вариант
Часть А
1. Упростите выражение а3 (а-2)3.
1) а-5; 2) а-3; 3) а-9; 4) а9.
2. Найдите значение выражения b – 54b-2, если b = 3.
1) –6; 2) 9; 3) –3; 4) 327.
3. Решите систему уравнений:
![]()
![]()
1) (3; -1); 2) (-1; 3); 3) (-2; 6); 4) (6; -2).
4. Сократите дробь: 9с2 - 1
2с+ 6с2
1)
![]()
![]() ;
2)
;
2) ![]() ; 3) 3с – 1; 4) 3с
+ 1.
; 3) 3с – 1; 4) 3с
+ 1.
5. Упростите выражение: 25 – (5 – 2с)2.
1) 20с + 4с2; 2) 10с – 4с2;
3) –20с + 4с2; 4) 20с – 4с2.
6.
Упростите выражение: ![]() +
+ ![]() + 5
+ 5![]() .
.
1)
14![]() ;
2) 50
;
2) 50![]() ; 3) 20
; 3) 20![]() ; 4) 24
; 4) 24![]() .
.
7. Решите систему неравенств:
![]()
1)
(∞; -8); 2) ![]() ;
;
3)
![]() +∞ ); 4)
(-∞;
+∞ ); 4)
(-∞; ![]() .
.
8. Через точку (0; -1) проходит график функции
1)
у = 1 – х2; 2) у = ![]() ; 3) у = х – 1; 4) у =
; 3) у = х – 1; 4) у = ![]() - 1.
- 1.
9.
![]() По графику квадратичной функции найдите все значения
аргумента, при которых значения функции неотрицательны.
По графику квадратичной функции найдите все значения
аргумента, при которых значения функции неотрицательны.
у
1) (∞; -1);
2)
 (∞;
(∞; ![]()
![]()
![]()
![]() ;
+∞);
;
+∞);
3)
![]() ; ∞); 4)
; ∞); 4) ![]() ;
+∞).
;
+∞).
![]() 0
0
-3 -2 -1 1 2 3 4 х
10. Упростите выражение: m + m2 + 9
m+3 9-m2
1)
![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
.
11.
Выразите из формулы S=![]() переменную b.
переменную b.
1) b = ![]() ;
2) b =
;
2) b = ![]() ;
;
3) b = ![]() - а; 4) b =
- а; 4) b = ![]() - a.
- a.
12. На рисунке изображен график движения пешехода из города М в город К. На каком расстоянии от города М пешеход устроил привал?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() S (км)
S (км)
![]()
![]()
![]()
![]()
![]()
![]()
![]() 14 К
14 К
![]() 12
12
![]() 10
10
![]()
![]()
![]() 8
8
![]() 6
6
![]() 4
4
![]() 2
2
![]() М
1 2 3 4 5 6 t(ч)
М
1 2 3 4 5 6 t(ч)
1) 8 км; 2) 4 км; 3) 2 км; 4) 5 км.
13.
Расположите в порядке возрастания числа ![]() ;
3
;
3![]() ; 4.
; 4.
1)
![]() ; 4; 3
; 4; 3![]() ; 2) 4;
; 2) 4; ![]() ; 3
; 3![]() ;
;
3)
3![]() ;
; ![]() ; 4; 4) 4; 3
; 4; 4) 4; 3![]() ;
; ![]() .
.
14. Катер прошел по течению реки 8 км и вернулся обратно, потратив на весь путь 5ч. Скорость течения реки 3 км/ч. какова собственная скорость катера?
Если собственную скорость катера обозначить буквой х, то можно составить уравнение:
1)
2,5(х+3)+2,5(х-3) = 8 2) ![]() +
+![]() = 5;
= 5;
3)
![]() +
+![]() =
8; 4)
=
8; 4) ![]() +
+![]() = 8.
= 8.
15. Соотношение соли и сахара в рассоле равно 5 : 2. Сколько сахара содержится в 210 г рассола?
1) 60 г; 2) 70г; 3) 42 г; 4) 105г.
16. Вычислите значение выражения:
( 1,47 • 10-5) : (4,2 • 10-8)
и приведите результат к стандартному виду.
1) 3,5 • 10-2; 2) 3,5 • 102; 3) 3,5 • 104; 4) 0,35 • 103.
17.
Решите неравенство х2 – 5х + 4 ![]() 0.
0.
1)
(∞; 4); 2) (-∞; ![]() ; 3)
; 3) ![]() ; 4) (-4; -1).
; 4) (-4; -1).
Часть В
1. Найдите 35% от числа 420.
2. Найдите положительный корень уравнения 17х2 – 51х = 0
3.
Решите уравнение ![]() -
- ![]() = 8
= 8
4. Найдите ординату точки пересечения графиков функций у=5х – 1 и у = 4х + 5.
5.
Найдите меньший корень
уравнения ![]() = 5 + х
= 5 + х
Часть С
1.Сократите дробь 4х2 + 5х + 1
2х + 8х2.
2. Задайте формулой квадратичную функцию, график которой – парабола с вершиной в точке Т (0; 4), проходящая через точку М (-3; -8).
Найдите сумму всех положительных членов арифметической прогрессии 11,3; 9,6; … .
Ответы
I вариант
А: 1. 2; 2. 3; 3. 1; 4. 1; 5. 4; 6. 3; 7. 4; 8. 3; 9. 2; 10. 4; 11. 3; 12. 1;
13. 2; 14. 4; 15. 4; 16. 2; 17. 3.
В: 1. 147; 2. 3; 3. –22; 4. 29; 5. –6.
С:
1. ![]() ;
2. у = -
;
2. у = -![]() х2
+ 4; 3. 43,4.
х2
+ 4; 3. 43,4.
АЛГЕБРА И НАЧАЛА АНАЛИЗА XI КЛАСС
I вариант
Часть А
1. Результат вычисления выражения
![]() (1,6
- 2
(1,6
- 2![]() -
- ![]()
![]() )
· (-3
)
· (-3![]() ) – 0,4 : (-1,25) равен:
) – 0,4 : (-1,25) равен:
1) 1; 2) 2; 3) 3; 4) 4; 5) 5.
2. Результат упрощения выражения
(
![]() +
+ ![]() ) :
) : ![]() +
+![]() имеет вид:
имеет вид:
1) –с – 1; 2) 1 – с; 3) 2 – с; 4) с – 1; 5) с –2.
3. Даны три точки: (1; -2), (-2; 1), (2; 3). Если две из них принадлежат графику функции у = ах + b, пересекающему ось Оу в точке с положительной ординатой, то значение параметра а равно:
1) –1; 2) 2; 3) 5; 4) 0,5; 5) 0,75.
4.
Число целых значений аргумента на
промежутке ![]() , при которых функция у =
2х2 – 8х + 2 принимает отрицательные значения, равно:
, при которых функция у =
2х2 – 8х + 2 принимает отрицательные значения, равно:
1) 0; 2) 1; 3) 2; 4) 3; 5) 4.
5. Если х0, у0 – решение системы уравнений
![]()
то сумма х0 + у0 равна:
1) 2; 2) 1; 3) –1; 4) –2; 5) –3.
6. Если х1 и х2 – корни уравнения –2х2 + 3х + 5 = 0, то значение выражения х1 + х2 + 2х1х2 равно:
1) 9; 2) –3,5; 3) 15; 4) –7,5; 5) 0.
7. Среднее арифметическое всех корней уравнения
(х-1)2 (х+2) + (1-х2) (х+3) = х2 + 4х – 5 равно:
1) 0,25; 2) 0,5; 3) 0,75; 4) –0,75; 5) –0,5.
8.
Если х0 – корень уравнения ![]() ·
·
![]() = х+1, то значение
выражения х0 + 2 равно:
= х+1, то значение
выражения х0 + 2 равно:
х0 – 2
1)
-![]() ; 2)
; 2) ![]() ; 3) –3; 4) 3; 5) 1.
; 3) –3; 4) 3; 5) 1.
9.
Количество целых положительных решений неравенства ![]()
![]()
![]() равно:
равно:
1) 2; 2) 3; 3) 4; 4) 5; 5) 1.
10. Сумма корней уравнения ׀6х – 5х2׀ = 1 равна:
1) –2,4; 2) –2,2; 3) –1,2; 4) 1,2; 5) 2,4.
11. Количество целых решений неравенства ׀׀х׀ - 2׀ < 1 равно:
1) 1; 2) 0; 3) 2; 4) 3; 5) 6.
12.
Наименьший положительный период
функции у = ![]() tg
tg![]() равен:
равен:
1) 2π; 2) 2π; 3) 21π; 4) 2π; 5) 4π.
7 3 4
13. Если sin α = 3 и 0 < α <π, то величина sin α равна:
2 5
1)
-![]() ;
2) -
;
2) -![]() ; 3) -
; 3) -![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]()
![]() .
.
5
14. Значение выражения cos ( π – arcsin 4) равно:
2 5
1)
-![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4) -
; 4) -![]() ; 5)
; 5) ![]() .
.
15. Сумма корней уравнения 2cos2x + sinx = 2, принадлежащих промежутку [π ; 9π], равна:
2![]() 8
8
1) 11π ; 2) 3π ; 3) 4π ; 4) 5π ; 5) π .
6 2 3 6 2
16.
Решением неравенства sin х ![]()
![]() , удовлетворяющим
условию
, удовлетворяющим
условию
2
х![]() [- π ; 5π
], является промежуток:
[- π ; 5π
], является промежуток:
2 4
1) [ π ; 3π ]; 2) [ -π ; 5π ]; 3) [ π ; 5π ]; 4)[ π ; 5π ]; 5) [ π ; π ].
4 4 4 4 4 4 2 4 4 2
17.
Область определения функции ![]() f(х)
= 1 имеет вид:
f(х)
= 1 имеет вид:
log5 (4-x) –1
1)
(-∞; 4); 2) (-∞; -1) ![]() (-1;
4); 3) (-1; ∞); 4) (-∞; 4)
(-1;
4); 3) (-1; ∞); 4) (-∞; 4) ![]() (4;
∞); 5) (4; ∞).
(4;
∞); 5) (4; ∞).
18.
Результат вычисления выражения 4 1-2log39+log5![]() равен:
равен:
1)
![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() .
.
19. Корень уравнения log2(x+4) + log2(x-3) = 3 принадлежит промежутку:
1) (-3; 1); 2) (-10; 0); 3) (1; 5); 4) [5; 12); 5) (-1; 3).
20. Множество решений неравенства (1,5)х * ( 2 )2х-1 > 4 имеет вид:
3 9
1)
( 3; ∞); 2) ( 2; ∞ ); 3) (- ∞; 3); 4) (-∞; 2) ![]() (4; ∞); 5) (6; ∞).
(4; ∞); 5) (6; ∞).
21. Количество целых решений неравенства log1/2(3x+1) > -3 равно:
1) 2; 2) 4; 3) 3; 4) 1; 5) 6.
22. Если касательная, проведенная к графику функции у = -2х2 + 5х, имеет угловой коэффициент, равный –2, то абсцисса точки касания равна:
1)
-![]() ; 2)
; 2) ![]() ; 3) -
; 3) -![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() .
.
23. Уравнение касательной, проведенной к графику функции у=х2 в точке с абсциссой х0=-1, имеет вид:
1) у = -2х + 1; 2) у = -2х; 3) у = -2х – 1; 4) у = -х – 1; 5) у = -х –1.
24. Точка максимума функции у = х3 – 3х2 – 45х равна:
1) -2; 2) –3; 3) –4; 4) –5; 5) –6.
25. Одна из первообразных функций 6sin3x равна:
1) 1 – 2cos3x; 2) –18cosx; 3) 18cosx; 4) 2cos3x; 5) 1 + 2sin3x.
26. Площадь криволинейной трапеции, ограниченной линиями
у = 4cosx, y = 0, x = 0, и х = π , равна:
6
1) 2; 2) 1; 3) 3; 4) 2,5; 5) 0,5.
Часть В.
1.
Найдите количество целых решений
неравенства 17х + 1 ![]() 1.
1.
8х2 + 8х + 15
2. Найдите сумму первых одиннадцати членов арифметической прогрессии, шестой член которой равен 6.
3. Найдите значение выражения х0(х0 + 2), если х0 – корень уравнения 5х – 7 · 5х-2 = 90.
4. Найдите наименьшее значение функции у = 3х2 – 12х – 16 на отрезке [3; 8].
Ответы:
А: 1. 4; 2. 4; 3. 4; 4. 3; 5. 3; 6. 2; 7. 4; 8. 4; 9. 4; 10. 5; 11. 3; 12. 4;
13. 4; 14. 3; 15. 1; 16. 1; 17. 2; 18. 3; 19. 3; 20. 3; 21. 3; 22. 5; 23. 3;
24. 2; 25. 1; 26. 1.
В: 1. 7; 2. 66; 3. 15; 4. 25.
2.4. Критерии оценки знаний и умений учащихся.
Учитель, опираясь на эти рекомендации, оценивает знания и умения учащихся с учетом их индивидуальных особенностей.
1. Содержание и объем материала, подлежащего проверке, определяется программой по математике для средней школы. При проверке этого материала следует выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях
2. Основными формами проверки знаний и умений учащихся по математике в средней школе являются письменная контрольная работа и устный опрос. При оценке письменных и устных ответов учитель в первую очередь учитывает показанные учащимися знания и умения (их полноту, глубину, прочность, использование в различных ситуациях). Оценка зависит так же от наличия и характера погрешностей, допущенных учащимися.
3. Среди погрешностей выделяются ошибки и недочеты. Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе. К недочетам относятся погрешности, свидетельствующие о недостаточно полном ил недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в соответствии с программой основными. Недочетами также являются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения; неаккуратная запись; небрежное выполнение чертежа. Граница между ошибками и недочетами является в некоторой степени условной. При одних обстоятельствах допущенная учащимися погрешность может рассматриваться учителем как ошибка, в другое время и при других обстоятельствах – как недочет.
4. Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач. Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а устное изложение и письменная запись ответа математически грамотны и отличаются последовательностью и аккуратностью. Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
5. Оценка ответа учащегося при устном и письменном опросе проводится по пятибальной системе.
Оценка устных ответов учащихся.
Ответ оценивается отметкой «5», если ученик:
- полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
- изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
- правильно выполнил рисунка, чертежи, графики, сопутствующие ответу;
- показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
- продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;
- отвечал самостоятельно, без наводящих вопросов учителя.
Возможны 1-2 неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
- в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;
- допущены 1-2 недочета при освещении основного содержания ответа, исправленные после замечания учителя;
- допущены ошибка или более 2 недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставиться в следующих случаях:
- неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы, достаточные для дальнейшего усвоения программного материала;
- имелись затруднения или допущены ошибки в определении понятия, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
- ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
- при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
- не раскрыто основное содержание учебного материала;
- обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
- допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
- ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.
Оценка письменных работ учащихся.
Отметка «5» ставится, если:
-работа выполнена полностью;
- в логических рассуждениях и обосновании решения нет пробелов и ошибок;
- в решении нет математических ошибок (возможна лдна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
- работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
- допущена одна ошибка или есть два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
- допущено более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
- допущены существенные ошибки, показавшие, что учащийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
- работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть выполнена не самостоятельно.
6. Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им каких либо других заданий.
Список использованной литературы
1. Абрамов А.И. и др. Концепция развития школьного математического образования // Математика в школе.1990.N 1. С. 15.
2. Акимова М.К. и др. Индивидуальность учащегося и индивидуальный подход. - М.: Знание, 1992. - 56с.
3. Алгебра и математический анализ для 9 класса: Учебное пособие для учащихся вход и классов с углубленным изучением математики/ Н.Я.Виленкин и др. - М.: Просвещение, 1983. -319с.
4. Алексеев С.В. Дифференциация в обучении предметам естественнонаучного цикла. - Л.: ЛГИУУ, 1991. -112с.
5. Антропова М.В. и др. Дифференцированное обучение : педагогическая и физиологическая оценка// Педагогика.1992. № 9-10.
6. Бабанский Ю.К. Введение в научное исследование по педагогике: Учебное пособие для студентов пединститутов/ Под ред. В.И.Журавлева.-: Просвещение.1988.С.91-106.
7. Башмаков М.И. Уровень и профиль школьного математического образования// Математика в школе.1993.N 2.С.8.
8. Богоявленский Д.Н. Приемы умственной деятельности и их формирование у школьников// Вопросы психологии.1969. № 2.С.25-38.
9. Болтянский В.Г., Глейзер Г.Д. К проблеме школьного математического образования// Математика в школе. 1988.N 3.С.9.
10. Бударный А.А. Индивидуальный подход в обучении//Советская педагогика.1965.А.N 7.С.18-20.
11. Виноградова Л.В. Развитие мышления учащихся при обучении математике. - Петрозаводск: Карелия,1989. - 163с.
12. Гальперин П.Я. К исследованию интеллектуального развития ребенка// Вопросы психологии.1969.N 1.С.12-15.
13.Государственные стандарты образования// Учительская газета. 1993.N 32.
14. Гурова Л.Л. Психологический анализ решения задач. - Воронеж: Изд-во Воронежского ун-та,1976. -327с.
15. Гусев В.А. Индивидуализация учебной деятельности учащихся как основа дифференцированного обучения математике в средней школе// Математика в школе.1990.N 4.С.19-21.
16. Гусев В.А. Методические основы дифференцированного обучения математике в средней школе: Автореф. ...дисс.докт.наук. - М., 1990. -39с.
17. Дидактика средней школы/ Под ред. М.Н.Скаткина. - М.: Просвещение,1982.-319с
18. Дифференциация как система. Ч.1.Ч.2. М.: Новая школа,1992
19. Дорофеев Г.В. и др. Дифференциация в обучении математике//Математика в школе.1990.N 4.С.15.
20. Епишева О.Б., Крупич В.И. Учить школьников учиться математике: Формирование приемов учебной деятельности: Кн. для учителя. - М.: Просвещение.1990. -128с.
21. Зыкова В.И. Познавательная деятельность учащихся со стойкой неуспеваемостью в условиях работы в экспериментальных классах// В кн.: Психологические проблемы неуспевающих школьников. - М.: Педагогика,1971. -287с.
22. Каким быть учебнику: Дидактические принципы построения/ Под ред. И.Я.Лернера, Н.М.Шахмаева. 4.1. 4.2. М.: Просвещение,1992. -36с., -42с.
23. Капиносов А.Н. Уровневая дифференциация при обучении математике в 5-9 классах// Математика в школе.1990.N 5.С.11-14.
24. Кирсанов А.А. Индивидуализация учебной деятельности школьников. - Казань,1980. -123с.
25.Колишев Н.С. Индивидуально - дифференцированный подход в процессе обучения старшеклассников: Автореф. ...дисс.канд.пед. - М.,1993. - 178с.
26. Колягин Ю.М. и др. Задачи в обучении математике. Ч.1.4.2. М.:Просвещение,1977. -110с., -142с.
27. Колягин Ю.М. и др. Профильная дифференциация в обучении математике// Математика в школе.1990.N 4.С.21.
28. Крупич В.И. Теоретические основы обучения решению школьных математических задач. - М.: Прометей,1995. -166с.
29. Крутецкий В.А. Психология математических способностей школьников. - М.: Просвещение,1968. -427с.
30. Куприянович В.В. Изучение способностей направляет дифференциацию// Математика в школе.1991.N 5.С.8-10.
31. Лященко Е.И. Проблема задач в школьном курсе математика// Задачи как цель и средство обучения математике учащихся средней школы - Л.,1981.С.3-13.
32. Машбиц Е.И. Психологический анализ учебной задачи// Советская педагогика.1973.N 2.С.58-65.
33. Менчинская Н.А. Краткий обзор состояния проблемы неуспевающих школьников// В кн.: Психологические проблемы неуспевающих школьников. - М.: Педагогика,1971. -196с.
34. Метельский Н.В. Пути совершенствования обучения математике:Проблемы современной методики математики.- Мн.: Университетское,1989. -149с.
35. Методика преподавания математики в средней школе: Общая методика/ Сост. Черкасов Р.С., Столяр А.А. - М.: Просвещение, 1995. -336.
36. Методика преподавания математики в средней школе: Частная методика: Учеб. пособие для студентов пед. ин-тов физ.-мат. спец./ А.Я.Блох, В.А.Гусев и др.: Сост. В.И.Мишин. - М.: Просвещение,1987. -416с.
37. Мордкович А.Г. Беседы с учителями математики. - М.: Школа-Пресс,1995. -272с.
38. Мурачковский Н.И. Как предупредить неуспеваемость школьников. Мн.: Нар.асвета,1977. -179с.
39.Обучение и развитие: Экспериментально-педагогическое исследование/ Под ред. Л.В.Занкова. - М.: Педагогика,1975. -407с.
40. Педагогическая энциклопедия. Том 1. - М.: Сов. энциклопедия.1964.С.760.
41. Педагогическая энциклопедия. Том 2. -М.: Сов. энциклопедия.1965.С.201.
42.Рабунский Е.С. Индивидуальный подход в процессе обучения школьников. - М.: Педагогика,1975. - 213с.
43. Рассудовская М.М. Домашнее задание для всего класса// Математика в школе.1984.N 6.С.19.
44. Рахимов А.З. Психодидактика. Учебное пособие. – Творчесто, Уфа, 1996
45. Рейтман У.Р. Познание и мышление: Моделирование на уровне информационных процессов: Пер. с англ./ Под ред. А.В.Напалкова. - М.: Нир.1968. -400с.
46. Рогановский Н. М. Каким быть дифференцированному учебнику// Математика в школе.1990.N З.С.17.
47. Саранцев Г.И. О методике обучения школьников поиску решения математических задач// Преподавание алгебры и геометрии в школе: Пособие для учителей/ Сост. О.А.Боковнев. - М.: Просвещение,1982.С.123-131.
48. Слепкань З.И. Психолого-педагогичиские основы обучения математике. - Киев: Рад.школа, 1983. -192с.
49. Смирнов В.А., Смирнова И.М. Активизация деятельности учащихся при изучении теории// Математика в школе.1992.N 1.С-19.
50. Сохор А.М. Логическая структура учебного материала: Автореф. ...докт.пед.наук. - М.,1974. -44с.
51.Столяр А.А. Педагогика математики. - Мн.: Высшая школа, 1986. -414с.
52. Унт Н.Э. Индивидуализация и дифференциация обучения. - М.:Педагогика,1990. -190с.
53. Фридман Л.М. Психолого-педагогические основы обучения математике в школе. - М.: Просвещение,1983. -160с.
54. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи.- М.: Просвещение, 1989. -191с.
55. Хамраев Ч. Деятельностный подход в процессе обучения решению планиметрических задач на вычисление: Дисс. ...канд.пед.наук.- Чарджев,1993. -224с.
56. Цетлин В.С. Предупреждение неуспеваемости учащихся. - М.:Знание,1989. -41с.
57. Шахмаев Н.Н. Учителю о дифференцированном обучении: Методические рекомендации. - М.: АПН СССР НИИ общей педагогики,1989. -64с.
58. Шарыгин И.Ф. Факультативный курс по математике. Решение задач. М.: Просвещение, 1989


 4
4 3
3