
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Реферат: Контрольная работа
Реферат: Контрольная работа
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Томский государственный университет систем управления
и радиоэлектроники (ТУСУР)
Кафедра Экономики
Контрольная работа
по дисциплине “Математические модели в Экономике ”
Вариант №18
Выполнил:
Студент гр. з822
________ Васенин П.К.
Проверила:
________ Сидоренко М.Г.
г. Томск 2003
Задание №1
1. Объём выпуска продукции Y зависит от количества вложенного труда x как функция
![]() .
Цена продукции v, зарплата p.
Другие издержки не учитываются. Найти оптимальное количество вложенного труда.
.
Цена продукции v, зарплата p.
Другие издержки не учитываются. Найти оптимальное количество вложенного труда.
Решение:
Оптимальное количество вложенного труда обозначим через X*
Определим прибыль ![]()
Воспользуемся соотношением ![]() - т.е. частные производные
приравняем к нулю, найдём оптимальное количество вложенного труда
- т.е. частные производные
приравняем к нулю, найдём оптимальное количество вложенного труда
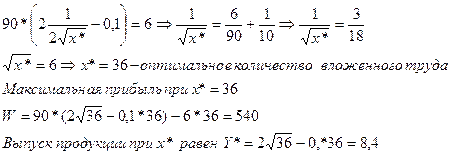
Задание №2
2. Даны зависимости спроса D=200-2p и предложения S=100+3p от цены. Найдите равновесную
цену, цену при которой выручка максимальна и эту максимальную выручку.
Решение:
Равновесная цена находится путём приравиевания спроса и предложения, т.е. 200-2p=100+3p; p*=20 – равновесная цена.
Найдём прибыль при равновесной цене:
![]()
Найдём цену, определяющую максимум выручки:
![]()
При p*(200-2p) максимум достигается в точке p’=50 (определили через производную)
W (50)=50*(200-2*50)=5000
Таким образом, максимальная выручка W(p’)=5000 достигается не при равновесной цене.
Задание №3
3. Найти
решение матричной игры (оптимальные стратегии и цену игры) ![]() .
.
Решение:
1- способ. Проверим на наличие седловой точки. Седловая точка является одновременно наименьшим элементом строки и наибольшим элементом столбца. В матрице седловой точки нет.
![]() Выигрыш
первого есть случайная величина с рядом распределения:
Выигрыш
первого есть случайная величина с рядом распределения:
![]()
Найдём средний выигрыш за партию Первого – это математическое ожидание случайной величины W(x,y):
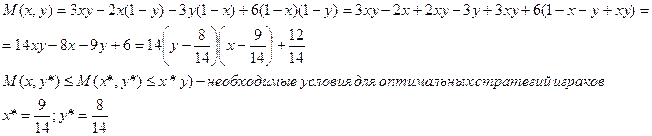
Оптимальные стратегии игроков:
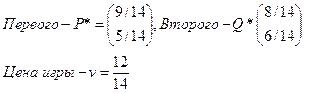
2 – способ. Если решить
эту игру как матричные игры двух игроков с нулевой суммой, то для игры с
матрицей ![]() оптимальные смешанные для 1
и 2 игроков и цена игры получаются из решения уравнений:
оптимальные смешанные для 1
и 2 игроков и цена игры получаются из решения уравнений:
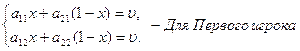
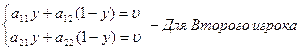
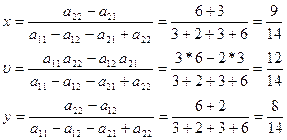
Откуда, Оптимальные стратегии игроков:
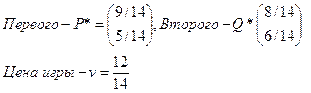
Задание №4
4. Для
трехотраслевой экономической системы заданы матрица коэффициентов прямых
материальных затрат 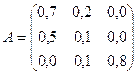 и вектор конечной
продукции
и вектор конечной
продукции 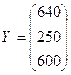 . Найти коэффициенты полных
материальных затрат двумя способами (с помощью формул обращения невыраженных
матриц и приближённо), заполнить схему межотраслевого баланса.
. Найти коэффициенты полных
материальных затрат двумя способами (с помощью формул обращения невыраженных
матриц и приближённо), заполнить схему межотраслевого баланса.
Решение:
I. Определим матрицу коэффициентов полных материальных затрат приближённо, учитывая косвенные затраты до 2-го порядка включительно.
Матрица косвенных затрат первого порядка:
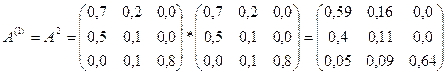
Матрица косвенных затрат второго порядка:
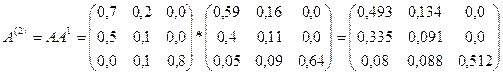
Получаем матрицу коэффициентов полных материальных затрат (приближённо):
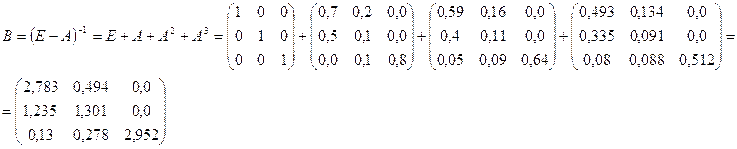
II. Определим матрицу коэффициентов полных материальных затрат с помощью формул обращения невыраженных матриц:
a) Находим матрицу (E-A):
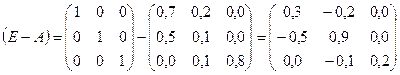
b) Вычисляем определитель этой матрицы:
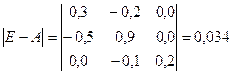
c) Транспонируем матрицу (E-A):
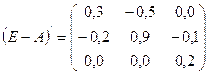
d) Находим алгебраические дополнение для элемента матрицы (E-A)’:
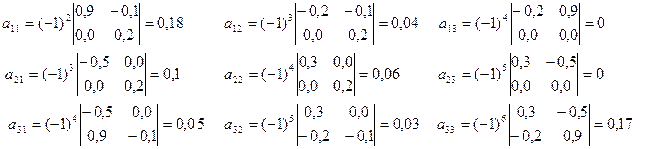
Таким образом:
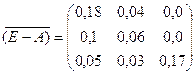
e) Находим матрицу коэффициентов полных материальных затрат:
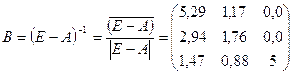
Таким образом, расчёты первым и вторым способом получились разные – это произошло из-за того, что второй способ наиболее точен (рассчитан по точным формулам), а первый способ рассчитан приближённо, без учёта косвенных затрат выше второго порядка.
Для заполнения межотраслевого баланса необходимо найти величину валовой продукции:
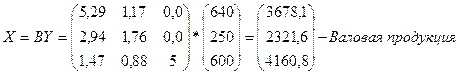
Схема межотраслевого баланса
|
Производящие отрасли |
Потребляющие отрасли |
||||
|
1 |
2 |
3 |
Конечная продукция |
Валовая продукция |
|
|
1 2 3 |
2574,67 1839,05 0 |
464,32 232,16 232,16 |
0 0 3328,64 |
640 250 600 |
3678,1 2321,6 4160,8 |
|
Условно чистая продукция |
-735,62 |
1392,96 |
832,16 |
1490 |
|
|
Валовая продукция |
3678,1 |
2321,6 |
4160,8 |
10160,5 |
|
Задание №5
5. Проверить
ряд ![]() на наличие выбросов методом
Ирвина, сгладить методом простой скользящеё средней с интервалом сглаживания 3,
методом экспоненциального сглаживания (а=0,1), представить результаты
графически, определить для ряда трендовую модель в виде полинома первой степени
(линейную модель), дайте точечный и интервальный прогноз на три шага вперёд.
на наличие выбросов методом
Ирвина, сгладить методом простой скользящеё средней с интервалом сглаживания 3,
методом экспоненциального сглаживания (а=0,1), представить результаты
графически, определить для ряда трендовую модель в виде полинома первой степени
(линейную модель), дайте точечный и интервальный прогноз на три шага вперёд.
Решение:
a) Проверим ряд на наличие выбросов методом Ирвина. Метод Ирвина Служит для выявления аномальных уровней, т.е. – это отдельное значение временного ряда которое не отвечает потенциальным возможностям исследуемой экономической системы и которое, оставаясь в качестве значения уровня ряда, оказывает существенное влияние на значение основных характеристик временного ряда, и на трендовую модель.
Для выявления аномальных уровней воспользуемся формулой:
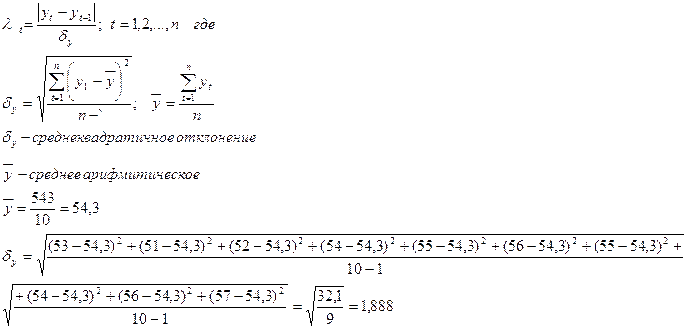
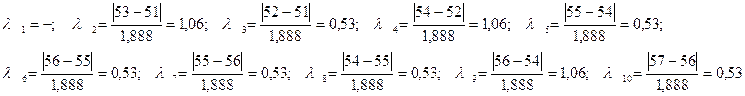 Расчётные значения:
Расчётные значения:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
|
- | 1,06 | 0,53 | 1,06 | 0,53 | 0,53 | 0,53 | 0,53 | 1,06 | 0,53 |
Необходимо, расчётные значения
сравнить с табличными критерия Ирвина ![]() ,
и если окажется, что расчётное больше табличного, то соответствующее значение
,
и если окажется, что расчётное больше табличного, то соответствующее значение ![]() уровня ряда считается
аномальным.
уровня ряда считается
аномальным.
Табличные значения для уровня значимости a=0,05, т.е. с 5% ошибкой:
| n | 2 | 3 | 10 | 20 | 30 | 50 | 100 |
|
|
2,8 | 2,3 | 1,5 | 1,3 | 1,2 | 1,1 | 1 |
Таким образом, при сравнении
значений, обнаруживаем, что аномальных уровней нет, т.е. ![]() .
.
b) Сгладим методом простой скользящей средней с интервалом сглаживания m=3:
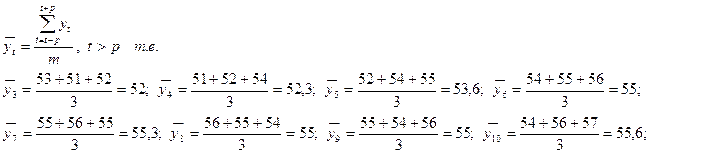
| t |
|
Метод простой
скользящей средней, |
| 1 | 53 | -- |
| 2 | 51 | -- |
| 3 | 52 | 52 |
| 4 | 54 | 52,3 |
| 5 | 55 | 53,6 |
| 6 | 56 | 55 |
| 7 | 55 | 55,3 |
| 8 | 54 | 55 |
| 9 | 56 | 55 |
| 10 | 57 | 55,6 |
c) Сгладим экспоненциальным методом с а=0,1 – параметр сглаживания:
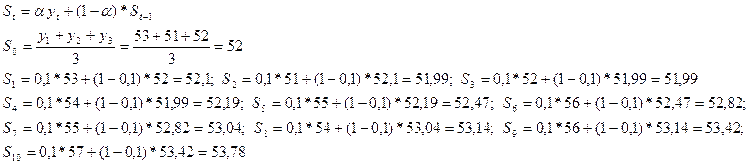
| t |
|
Экспоненциальный
метод, |
| 1 | 53 | 52,1 |
| 2 | 51 | 51,99 |
| 3 | 52 | 51,99 |
| 4 | 54 | 52,19 |
| 5 | 55 | 52,47 |
| 6 | 56 | 52,82 |
| 7 | 55 | 53,04 |
| 8 | 54 | 53,14 |
| 9 | 56 | 53,42 |
| 10 | 57 | 53,78 |
d) Представим результаты графически:
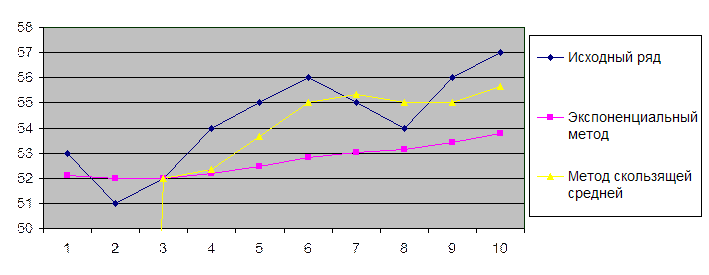
e) Определим для ряда трендовую модель в виде полинома первой степени (линейную модель):
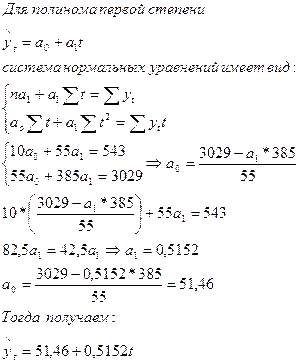
Необходимо оценить адекватность и точность построения модели, т.е. необходимо выполнение следующих условий:
a) Проверка случайности колебаний уровней остаточной последовательности:
![]()
Проверку
случайности уровней ряда проведем по критерию пиков, должно выполняться:![]()
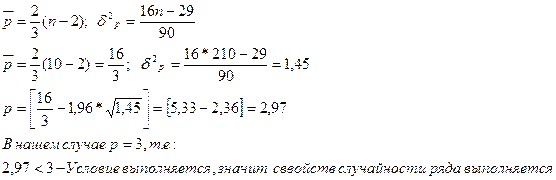
| t |
Фактическое |
Расчётное |
Отклонение |
Точки пиков |
|
1 2 3 4 5 6 7 8 9 10 |
53 51 52 54 55 56 55 54 56 57 |
51,97 52,49 53 53,52 54,03 54,55 55,06 55,58 56,09 56,61 |
1,03 -1,49 -1 0,48 0,97 1,45 -0,06 -1,58 -0,09 0,39 |
-- 1 0 0 0 1 0 1 0 -- |
| 55 | 543 | 542,9 | 0,1 | 3 |
b) Проверка соответствия распределения случайной компоненты нормальному закону распределения:
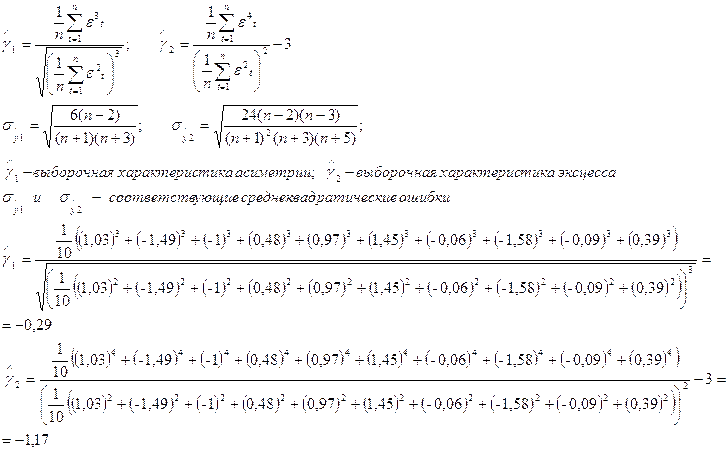
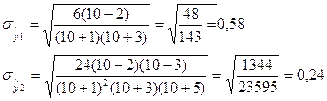
Необходимые условия:
![]()
Если эти условия выполняются одновременно, то гипотеза о характере распределения случайной компоненты принимается, если выполняется хотя бы одно из следующих неравенств:
![]()
то гипотеза о нормальном распределении отвергается, трендовая модель признаётся неадекватной.
1)![]()
2)![]()
Таким образом, одно из неравенств не выполняется, трендовая модель неадекватна, значит, дальнейшее исследование не имеет смысла.
Задание №6
6. Пункт
по приёму квартир работает в режиме отказа и состоит из двух бригад.
Интенсивность потока ![]() ,
производительность пункта
,
производительность пункта ![]() .
Определить вероятность того, что оба канала свободны, один канал занят, оба
канала заняты, вероятность отказа, относительную и абсолютную пропускную
способности, среднее число занятых бригад.
.
Определить вероятность того, что оба канала свободны, один канал занят, оба
канала заняты, вероятность отказа, относительную и абсолютную пропускную
способности, среднее число занятых бригад.
Решение:
Коэффициент использования (количество заявок, поступающих за время использования одной заявки)
![]()
a) Вероятность того, что оба канала свободны:
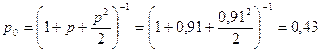
b) Вероятность того, что один канала занят:
![]()
c) Вероятность того, что оба канала заняты:
![]()
d) Вероятность отказа в заявке:
![]()
e) Относительная пропускная способность:
![]()
f) Абсолютная пропускная способность:
![]()
g) Среднее число занятых бригад:
![]()