
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Реферат: Цепные дроби
Реферат: Цепные дроби
Содержание
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава I. ПРАВИЛЬНЫЕ КОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ
§1. Представление рациональных чисел цепными дробями
§2. Подходящие дроби. Их свойства . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава II. БЕСКОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ
§1. Представление действительных иррациональных чисел правильными бесконечными цепными дробями
1.1. Разложение действительного иррационального числа в правильную бесконечную цепную дробь . . . . . . . . . . . . . . . . . . . . .
1.2. Сходимость правильных бесконечных цепных дробей . . . . .
1.3. Единственность представления действительного иррационального числа правильной бесконечной цепной дробью
§2. Приближение действительного числа рациональными дробями с заданным ограничением для знаменателя
2.1. Оценка погрешности при замене действительного числа его подходящей дробью . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2. Приближение действительного числа подходящими дробями
2.3. Теорема Дирихле . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4. Подходящие дроби как наилучшие приближения
§3. Квадратические иррациональности и периодические цепные дроби . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§4. Представление действительных чисел цепными дробями общего вида . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Решение задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Используемая литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Введение
Целью моей курсовой работы является исследование теории цепных дробей. В ней я попытаюсь раскрыть свойства подходящих дробей, особенности разложения действительных чисел в неправильные дроби, погрешности, которые возникают в результате этого разложения, и применение теории цепных дробей для решения ряда алгебраических задач.
Цепные дроби были введены в 1572 году итальянским математиком Бомбелли. Современное обозначение непрерывных дробей встречается у итальянского математика Катальди в 1613 году. Величайший математик XVIII века Леонардо Эйлер первый изложил теорию цепных дробей, поставил вопрос об их использовании для решения дифференциальных уравнений, применил их к разложению функций, представлению бесконечных произведений, дал важное их обобщение.
Работы Эйлера по теории цепных дробей были продолжены М. Софроновым (1729-1760), академиком В.М. Висковатым (1779-1819), Д. Бернулли (1700-1782) и др. Многие важные результаты этой теории принадлежат французскому математику Лагранжу, который нашел метод приближенного решения с помощью цепных дробей дифференциальных уравнений.
Глава I. Правильные конечные цепные дроби.
§1. Представление рациональных чисел цепными дробями.
Целое
число, являющееся
делителем
каждого из
целых чисел
![]() ,
называется
общим делителем
этих чисел.
Общий делитель
этих чисел
называется
их наибольшим
общим делителем,
если он делится
на всякий общий
делитель данных
чисел.
,
называется
общим делителем
этих чисел.
Общий делитель
этих чисел
называется
их наибольшим
общим делителем,
если он делится
на всякий общий
делитель данных
чисел.
Пусть
![]() - рациональное
число, причем
b>0.
Применяя к a
и
b
алгоритм
Евклида для
определения
их наибольшего
общего делителя,
получаем конечную
систему равенств:
- рациональное
число, причем
b>0.
Применяя к a
и
b
алгоритм
Евклида для
определения
их наибольшего
общего делителя,
получаем конечную
систему равенств:
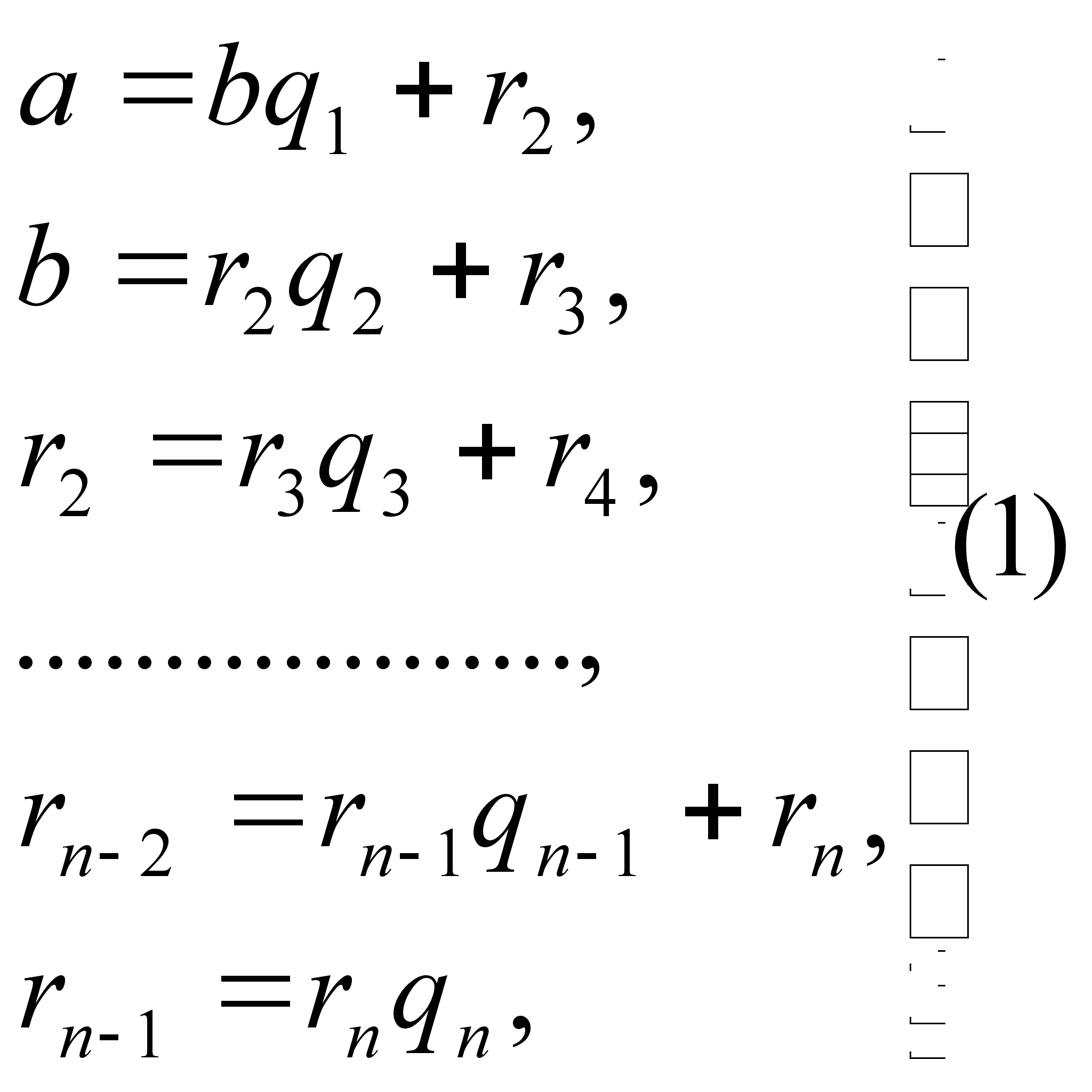
где
неполным частным
последовательных
делений
![]() соответствуют
остатки
соответствуют
остатки
![]() с условием
b>
с условием
b>![]() >
>![]() >…>
>…>![]() >0,
а соответствует
остаток 0.
>0,
а соответствует
остаток 0.
Системе равенств (1) соответствует равносильная система
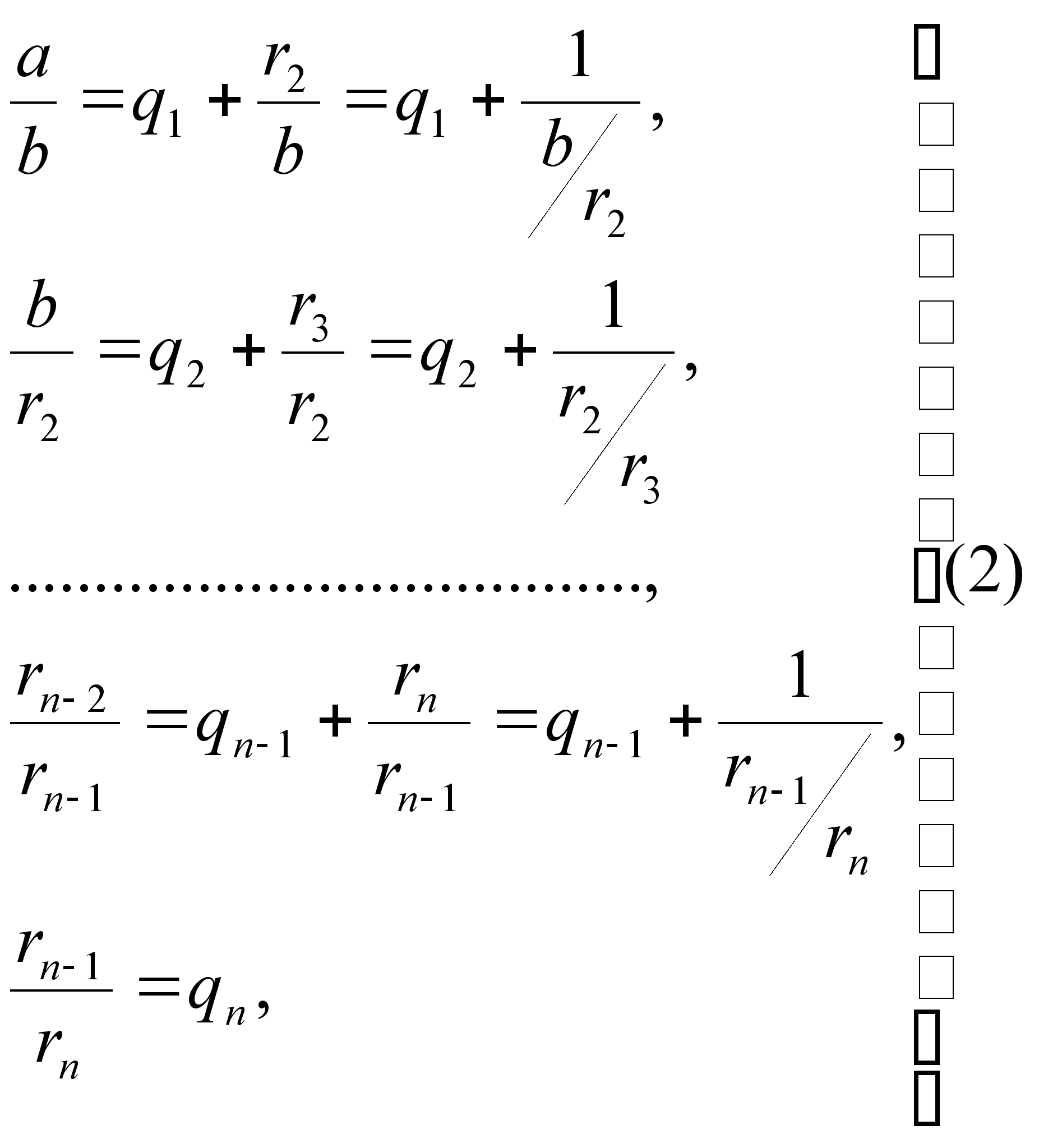
из
которой последовательной
заменой каждой
из дробей
![]() и т.д. ее соответствующим
выражением
из следующей
строки получается
представление
дроби
и т.д. ее соответствующим
выражением
из следующей
строки получается
представление
дроби
![]() в виде:
в виде:
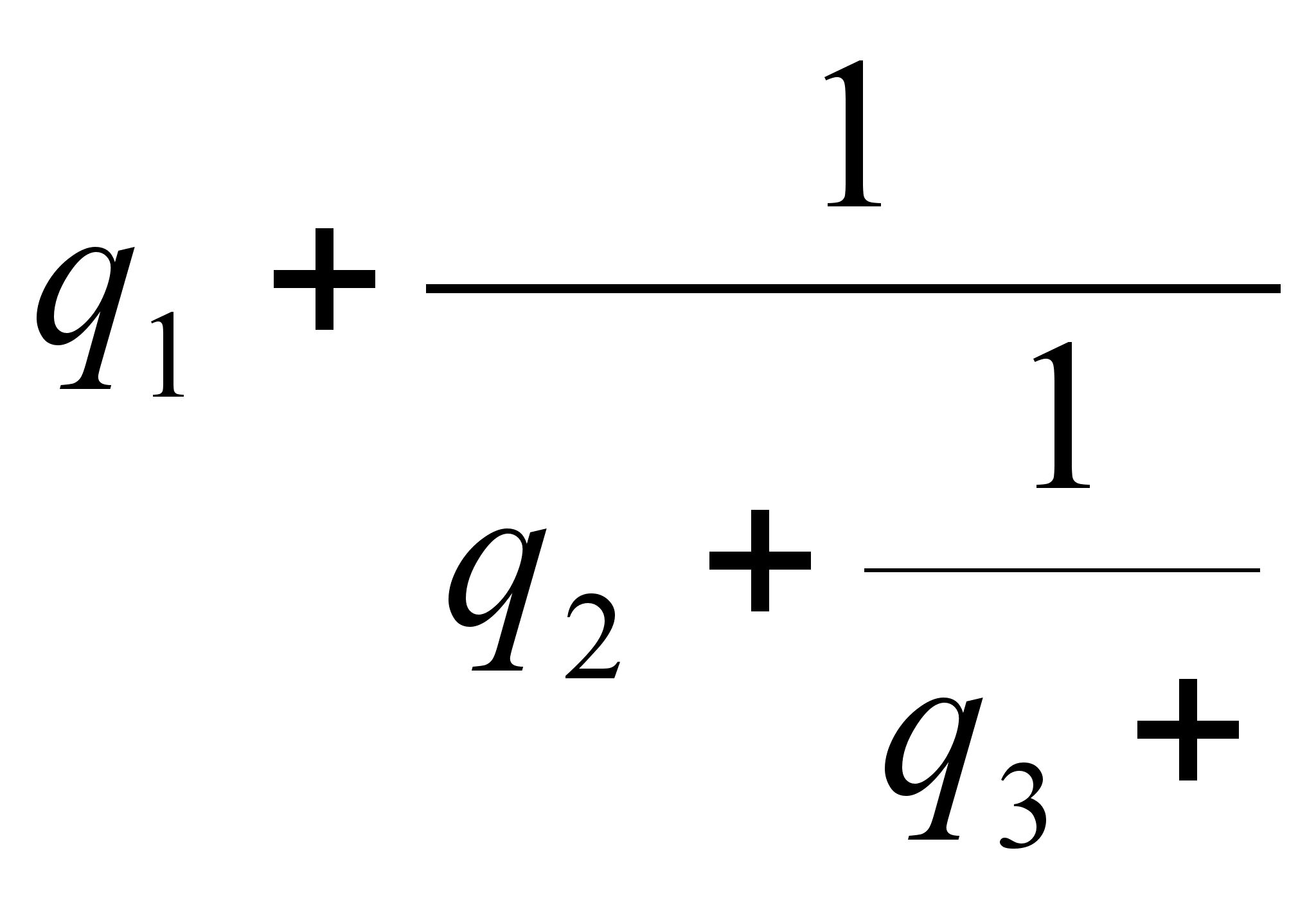
![]()
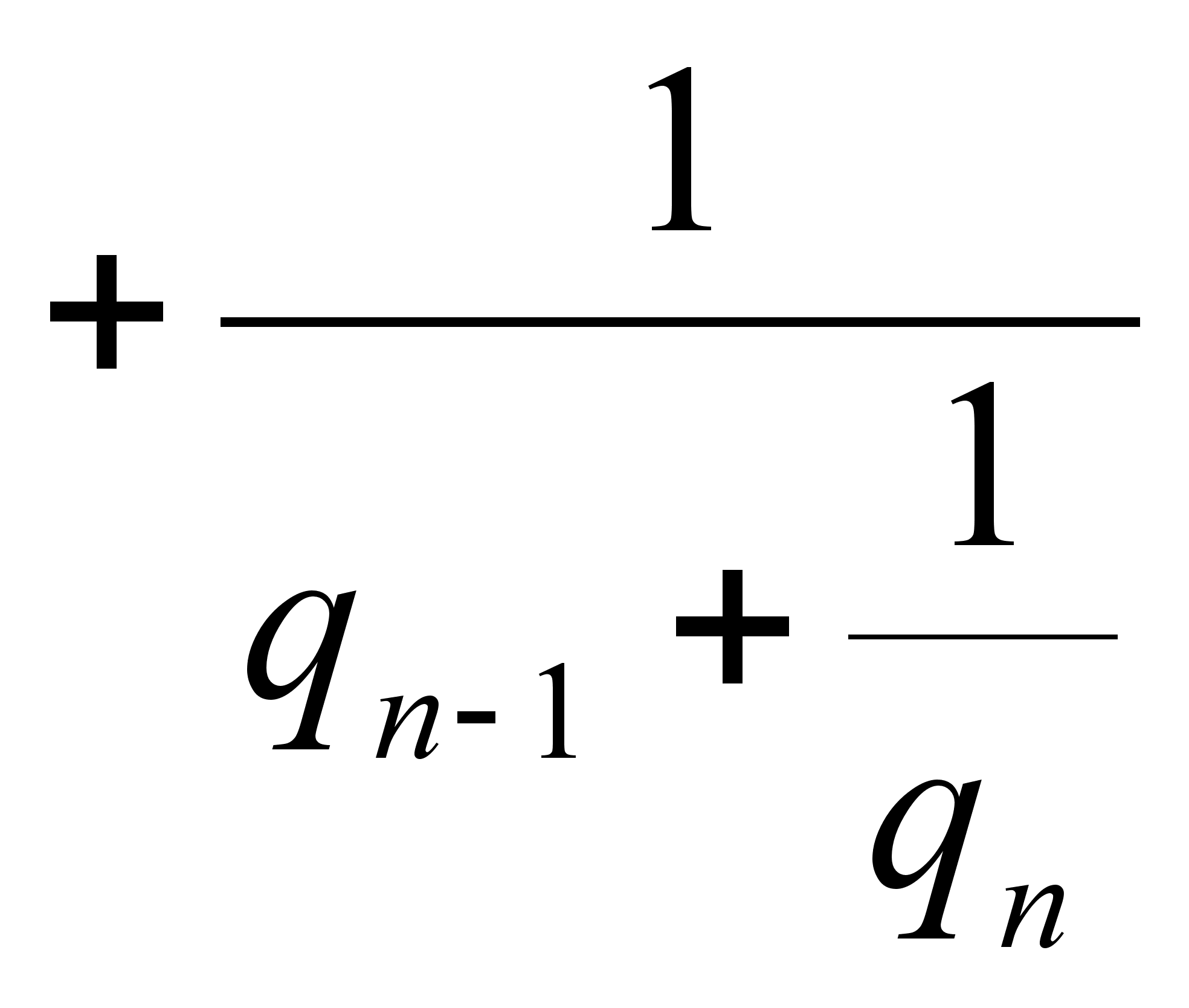
Такое
выражение
называется
правильной
(конечной) цепной
или правильной
непрерывной
дробью, при
этом предполагается,
что
![]() – целое число,
а
– целое число,
а
![]() ,
…,
,
…,
![]() - натуральные
числа.
- натуральные
числа.
Имеются различные формы записи цепных дробей:

![]()
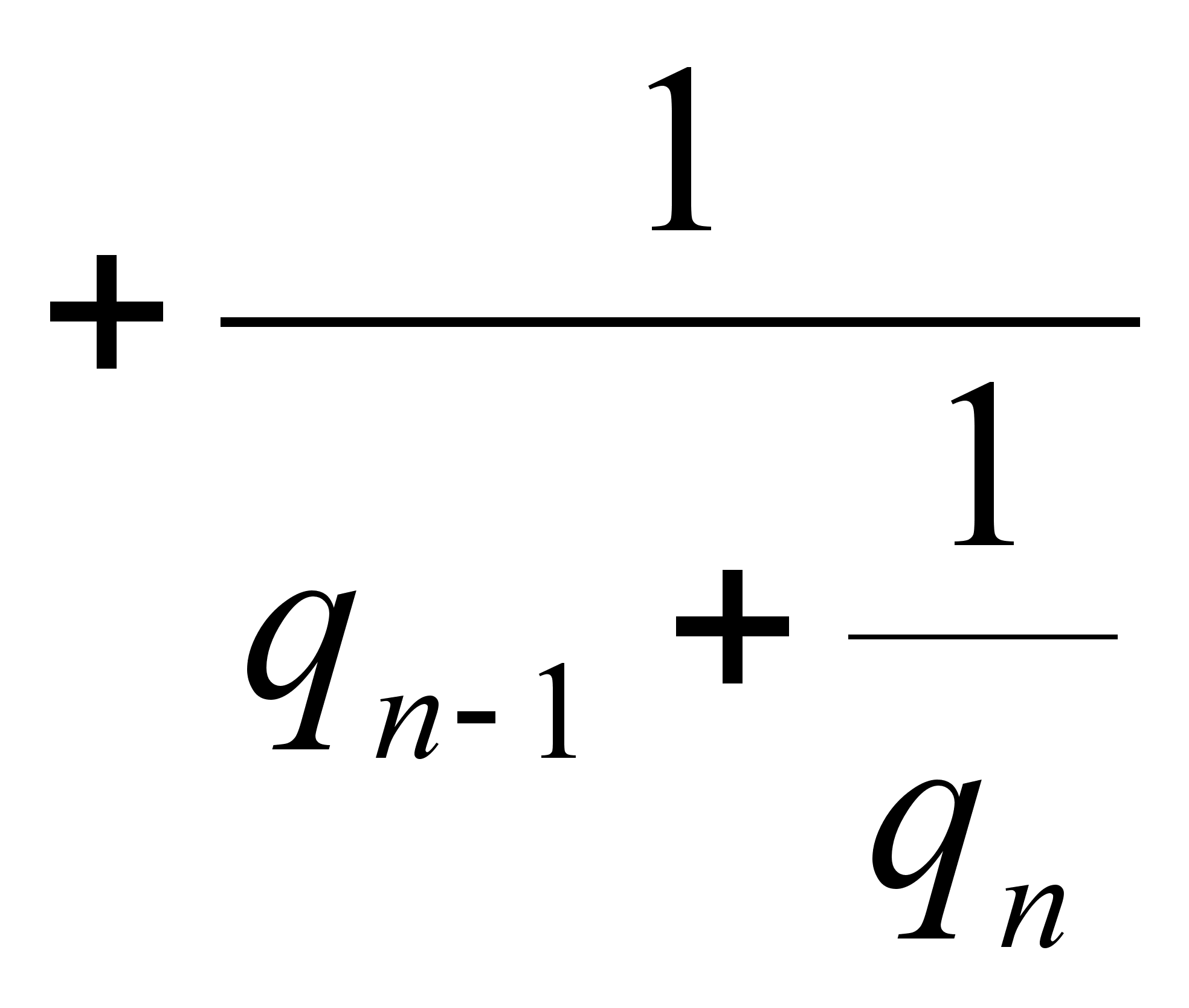
![]()
![]()
Согласно последнему обозначению имеем
![]()
Числа
![]() ,
,
![]() ,
…,
,
…,
![]() называются
элементами
цепной дроби.
называются
элементами
цепной дроби.
Алгоритм Евклида дает возможность найти представление (или разложение) любого рационального числа в виде цепной дроби. В качестве элементов цепной дроби получаются неполные частные последовательных делений в системе равенств (1), поэтому элементы цепной дроби называются также неполными частными. Кроме того, равенства системы (2) показывают, что процесс разложения в цепную дробь состоит в последовательном выделении целой части и перевертывании дробной части.
Последняя точка зрения является более общей по сравнению с первой, так как она применима к разложению в непрерывную дробь не только рационального, но и любого действительного числа.
Разложение
рационального
числа
![]() имеет, очевидно,
конечное число
элементов, так
как алгоритм
Евклида последовательного
деления
a
на
b
является конечным.
имеет, очевидно,
конечное число
элементов, так
как алгоритм
Евклида последовательного
деления
a
на
b
является конечным.
Понятно,
что каждая
цепная дробь
представляет
определенное
рациональное
число, то есть
равна определенному
рациональному
числу. Но возникает
вопрос, не имеются
ли различные
представления
одного и того
же рационального
числа цепной
дробью? Оказывается,
что не имеются,
если потребовать,
чтобы было
![]() .
.
Теорема.
Существует
одна и только
одна конечная
цепная дробь,
равная данному
рациональному
числу, но при
условии, что
![]() .
.
Доказательство:
1) Заметим, что
при отказе от
указанного
условия единственность
представления
отпадает. В
самом деле, при
![]() :
:
![]()
так что представление можно удлинить:
![]()
например, (2, 3, 1, 4, 2)=( 2, 3, 1, 4, 1, 1).
2)
Принимая условие
![]() ,
можно утверждать,
что целая часть
цепной дроби
,
можно утверждать,
что целая часть
цепной дроби
![]() равна ее первому
неполному
частному
равна ее первому
неполному
частному
![]() .
В самом деле:
.
В самом деле:
если n=1, то
если n=2, то
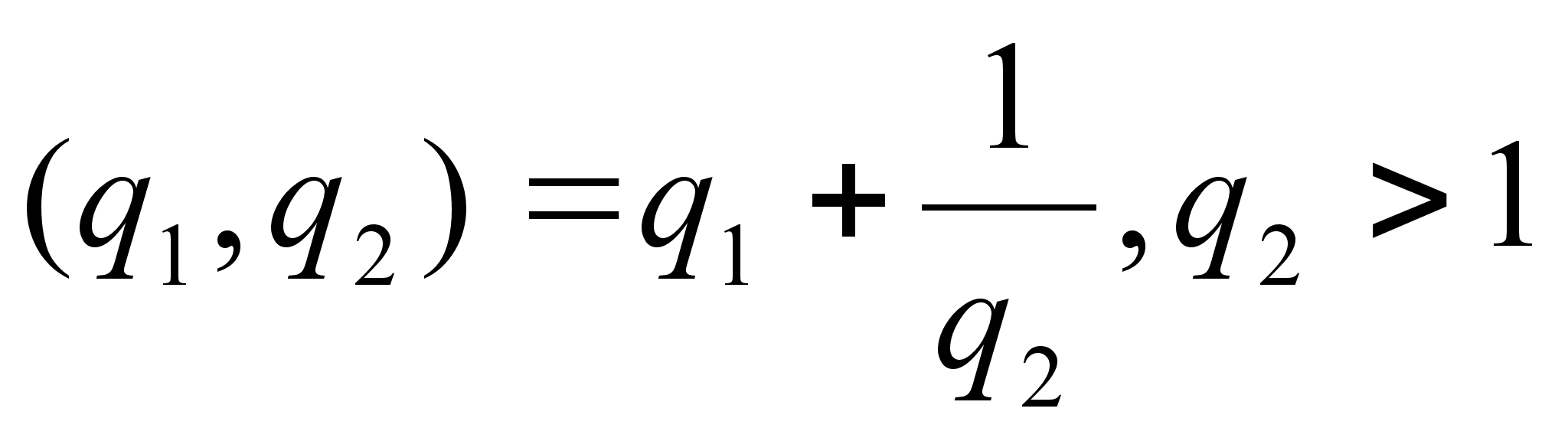 ;
поэтому
;
поэтому
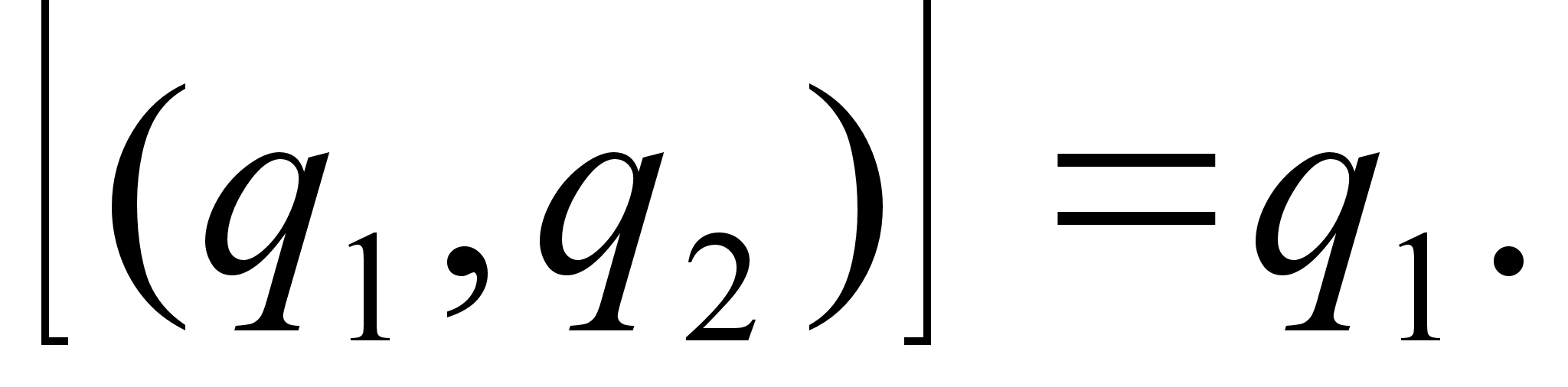
если n>2, то
![]() =
=![]()
![]()
![]() ,
,
где
![]() >1, т.к.
>1, т.к.
![]()
![]()
![]()
Поэтому
и здесь
![]() .
Докажем то, что
рациональное
число
.
Докажем то, что
рациональное
число
![]() однозначно
представляется
цепной дробью
однозначно
представляется
цепной дробью
![]() ,
если
,
если
![]() .
.
Пусть
![]() с условием
с условием
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
так что
,
так что
![]() .
Повторным
сравнением
целых частей
получаем
.
Повторным
сравнением
целых частей
получаем
![]() ,
а следовательно
,
а следовательно
![]() и так далее.
Если
и так далее.
Если
![]() ,
то в продолжении
указанного
процесса получим
также
,
то в продолжении
указанного
процесса получим
также
![]() .
Если же
.
Если же
![]() ,
например
,
например
![]() ,
то получим
,
то получим
![]() ,
что невозможно.
,
что невозможно.
Теорема доказана.
Вместе
с тем мы установили,
что при соблюдении
условия
![]() между рациональными
числами и конечными
цепными дробями
существует
взаимно
однозначное
соответствие.
между рациональными
числами и конечными
цепными дробями
существует
взаимно
однозначное
соответствие.
Замечания:
В случае разложения правильной положительной дроби первый элемент
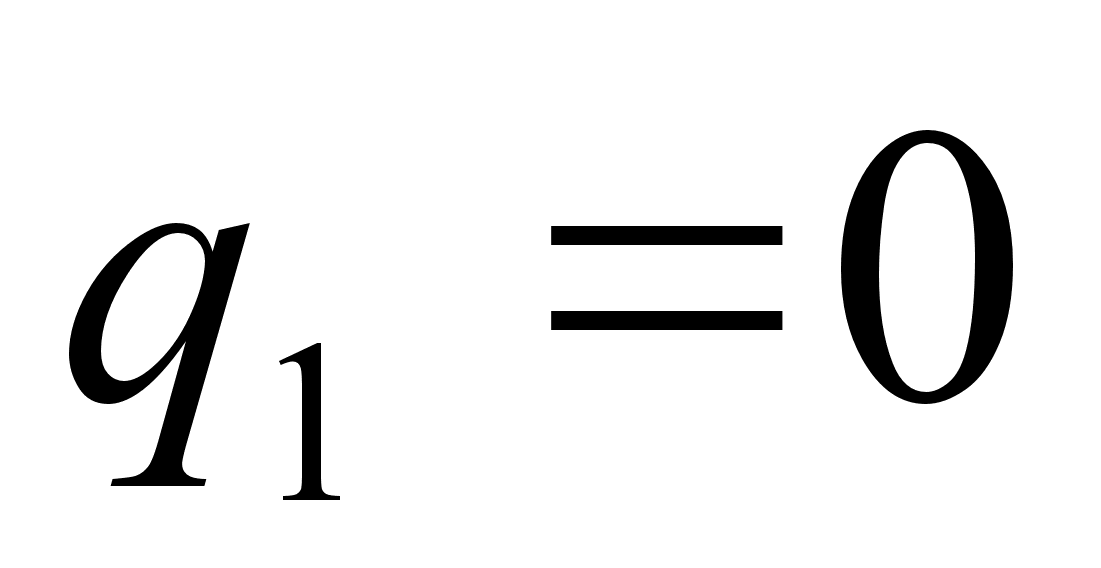 ,
например,
,
например,
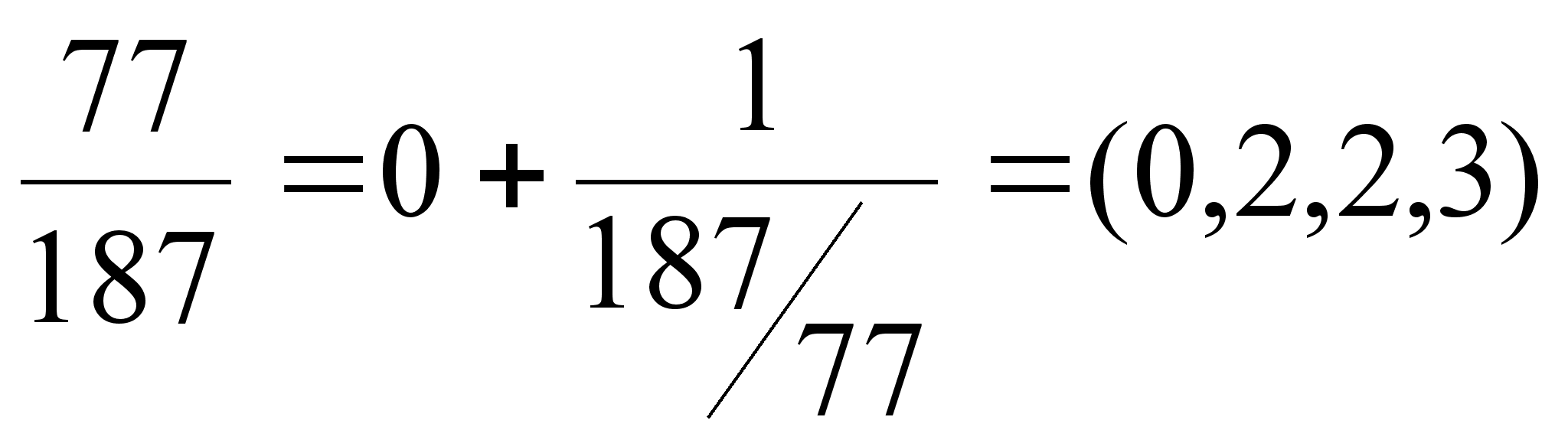 .
.При разложении отрицательной дроби (отрицательный знак дроби всегда относится к числителю) первый элемент будет отрицательным, остальные положительными, так как целая часть отрицательной дроби является целым отрицательным числом, а ее дробная часть, как всегда, положительна.
Пример:
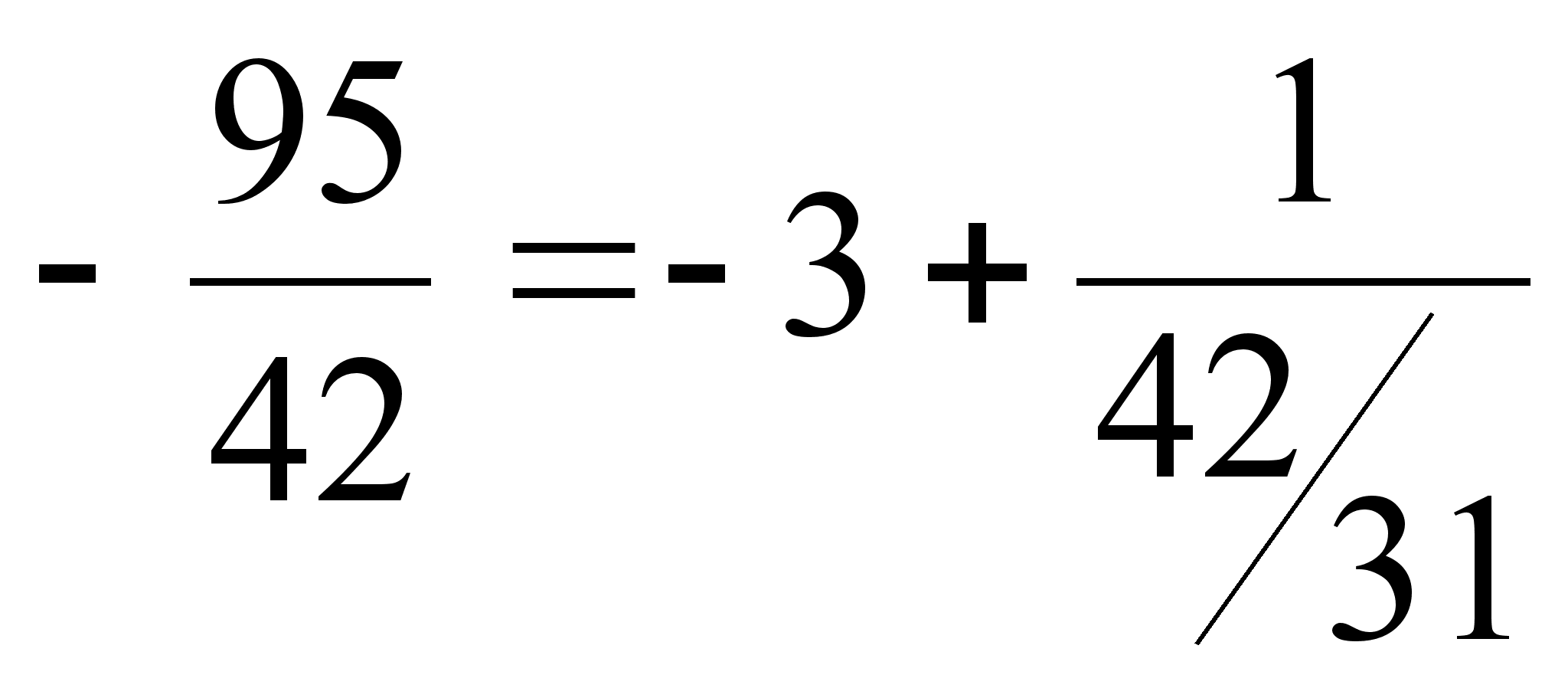 ,
а так как
,
а так как
![]() ,
то
,
то
![]() .
.
Всякое целое число можно рассматривать как непрерывную дробь, состоящую из одного элемента.
Пример:
5=(5);
![]() .
.
§2. Подходящие дроби. Их свойства.
Задаче
разложения
обыкновенной
дроби в непрерывную
дробь противостоит
обратная задача
– обращения
или свертывания
цепной дроби
![]() в простую дробь
в простую дробь
![]() .
.
При этом основную роль играют дроби вида:
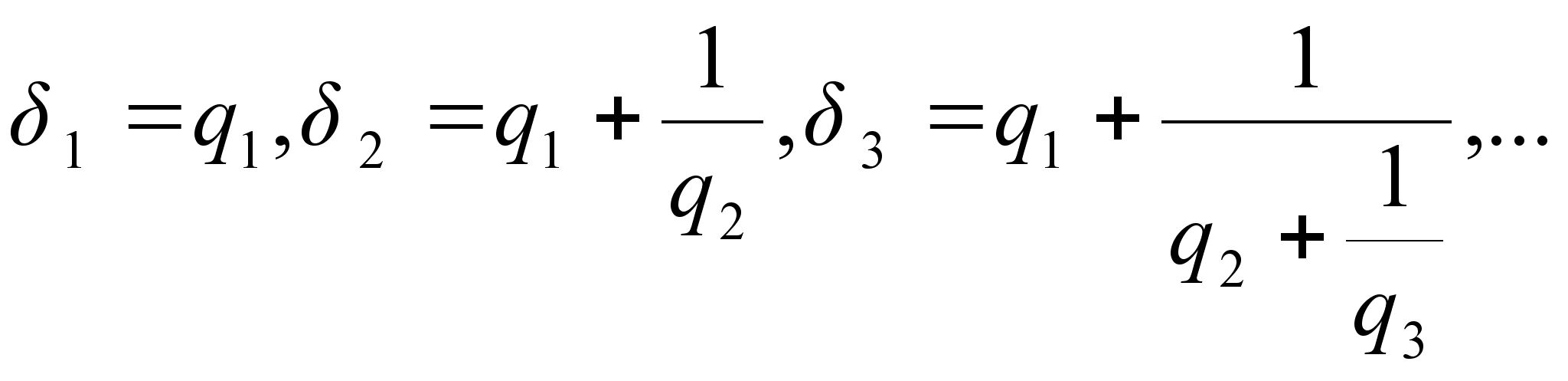 или
или
![]() которые
называются
подходящими
дробями данной
непрерывной
дроби или
соответствующего
ей числа
которые
называются
подходящими
дробями данной
непрерывной
дроби или
соответствующего
ей числа
![]() .
.
Заметим,
что
![]() =
=![]() =
=![]() .
Считается, что
подходящая
дробь
.
Считается, что
подходящая
дробь
![]() имеет порядок
k.
имеет порядок
k.
Прежде
чем приступить
к вычислению
подходящих
дробей заметим,
что
![]() переходит в
переходит в
![]() ,
если в первой
заменить
,
если в первой
заменить
![]() выражением
выражением
![]() .
.
Имеем
![]() ,
,
![]() ,
,
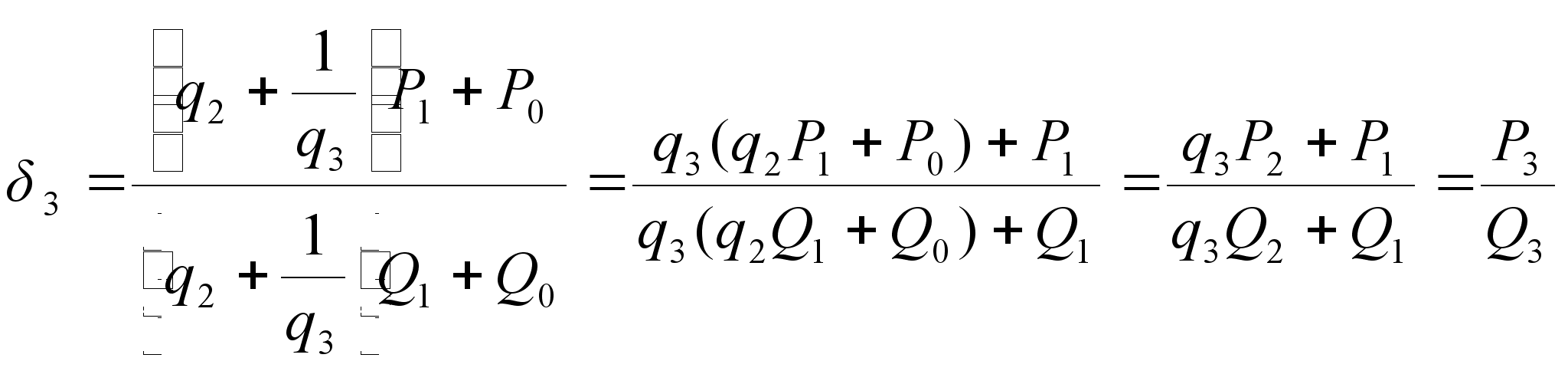 ,
…,
,
…,
при
этом принимается,
что
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() и так далее.
и так далее.
Закономерность,
которую мы
замечаем в
построении
формулы для
![]() (ее
числителя
(ее
числителя
![]() и знаменателя
и знаменателя
![]() ),
сохраняется
при переходе
к
),
сохраняется
при переходе
к
![]() и сохранится
также при переходе
от
k
к (k+1).
и сохранится
также при переходе
от
k
к (k+1).
Поэтому,
на основании
принципа
математической
индукции, для
любого k,
где
![]() ,
имеем
,
имеем
![]() (1),
(1),
причем
![]() (2)
(2)
![]() (3)
(3)
Далее,
говоря о подходящих
дробях
![]() (в свернутом
виде), мы будем
иметь в виду
их форму
(в свернутом
виде), мы будем
иметь в виду
их форму
![]() .
.
Соотношения
(1) являются
рекуррентными
формулами для
вычисления
подходящих
дробей, а также
их числителей
и знаменателей.
Из формул для
числителя и
знаменателя
сразу видно,
что при увеличении
k
они возрастают.
Последовательное
вычисление
числителей
![]() и знаменателей
и знаменателей
![]() подходящих
дробей по формулам
(2) и (3) удобно
располагать
по схеме:
подходящих
дробей по формулам
(2) и (3) удобно
располагать
по схеме:
|
|
|
… |
|
|
|
… |
|
||
|
|
|
|
|
… |
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
… |
|
Пример: Найти подходящие дроби к цепной дроби (2, 2, 1, 3, 1, 1, 4, 3).
|
2 |
2 |
1 |
3 |
1 |
1 |
4 |
3 |
|
|
|
2 |
5 |
7 |
26 |
33 |
59 |
269 |
866 |
|
|
1 |
2 |
3 |
11 |
14 |
25 |
114 |
367 |
Подходящие
дроби
![]() (
(![]() )
равны
соответственно
)
равны
соответственно
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Практически
нахождение
неполных частных
и подходящих
дробей удобно
объединить
в одну краткую
схему, которую
приведем для
![]() =(2,
3, 1, 4, 2)
=(2,
3, 1, 4, 2)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
А сейчас рассмотрим ряд свойств подходящих дробей.
Теорема: При k=1, 2, …, n выполняется равенство
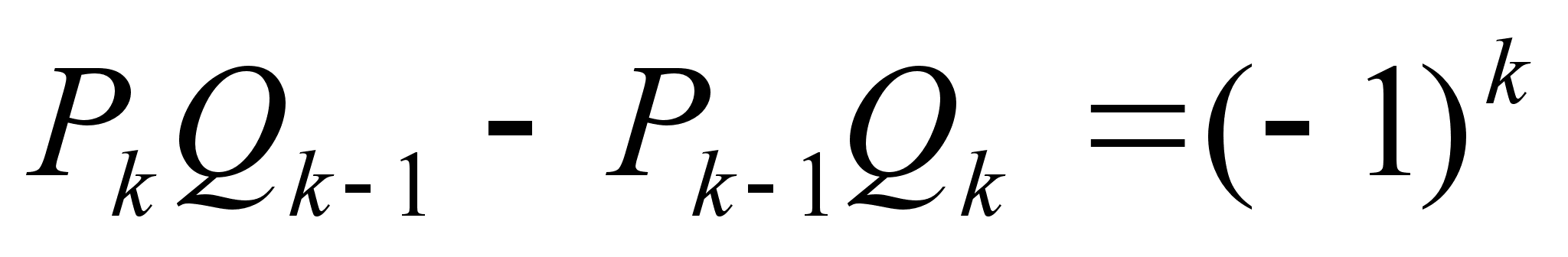
Доказательство: Проведем индукцию по k:
При k=1
равенство
справедливо,
так как
![]()
![]() .
.
Пусть
это равенство
верно при некотором
k=n
(![]() ).
).
Докажем справедливость равенства при k=n+1.
![]()
![]()
, то есть равенство верно при k=n+1.
Согласно
принципу полной
математической
индукции равенство
верно для всех
k(![]() ).
).
Теорема: Числитель и знаменатель любой подходящей дроби – взаимно простые числа, то есть всякая k–подходящая дробь несократима.
Доказательство:
Докажем это
свойство методом
от противного.
По предыдущему
свойству имеем
![]() .
.
Пусть
![]() ,
то есть
,
то есть
![]() ,
тогда из равенства
,
тогда из равенства
![]() следует,
что
следует,
что
![]() делится на
делится на
![]() без остатка,
что невозможно.
Значит, наше
допущение
неверно, а верно
то, что требовалось
доказать, то
есть
без остатка,
что невозможно.
Значит, наше
допущение
неверно, а верно
то, что требовалось
доказать, то
есть
![]() .
.
Теорема: При
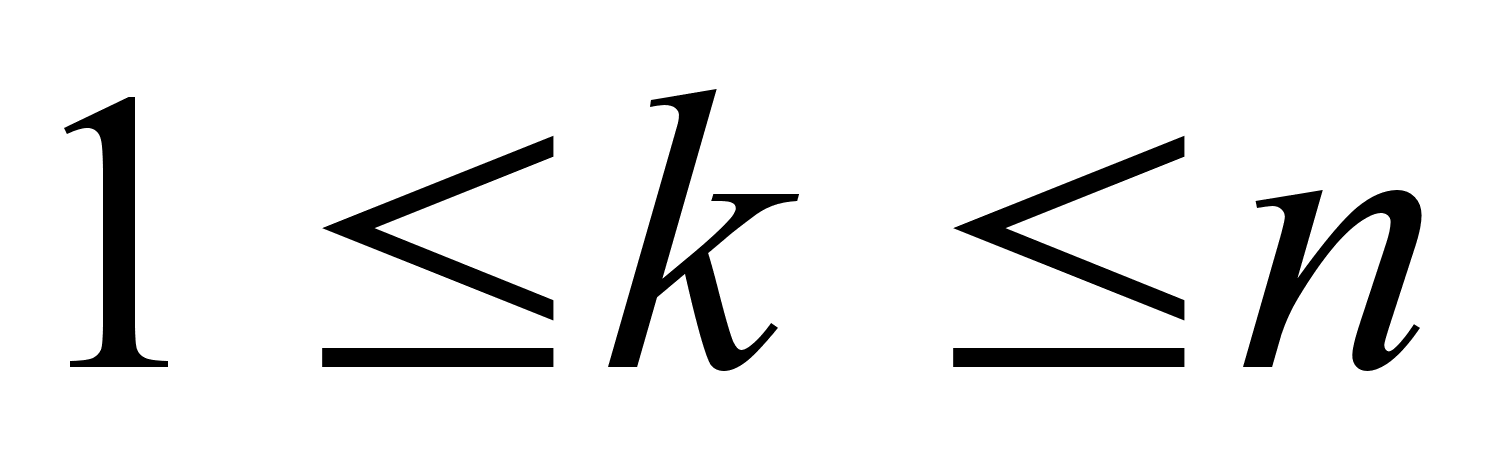
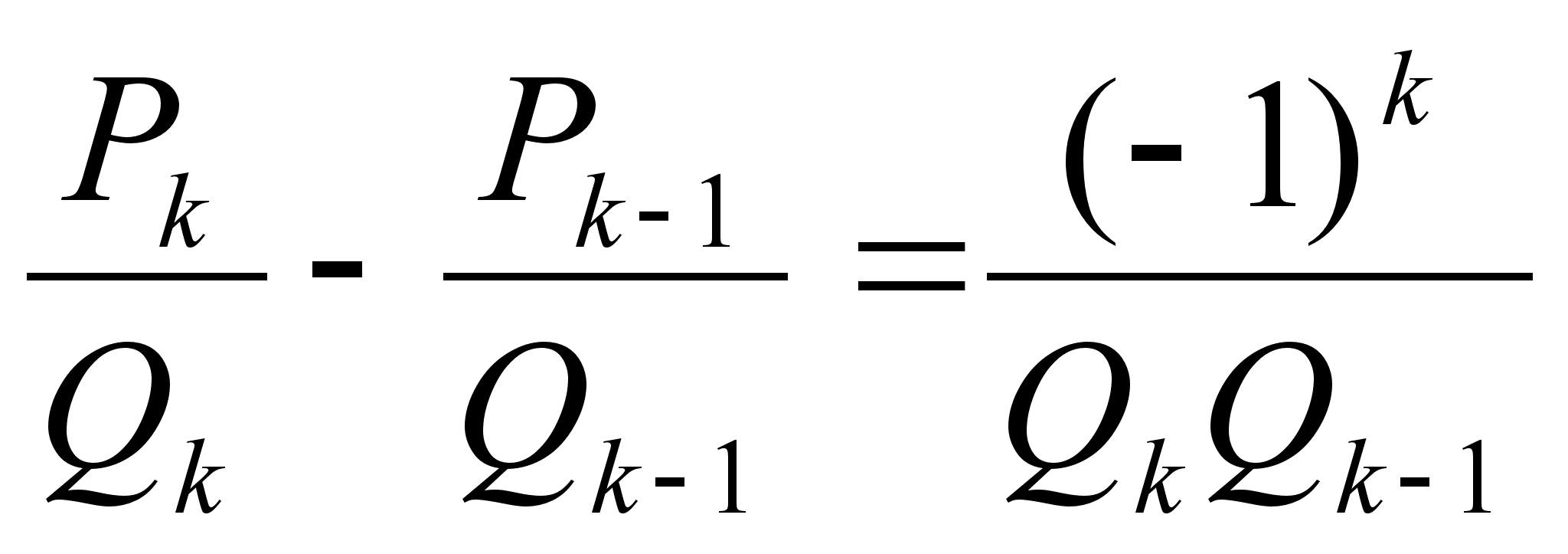 (
(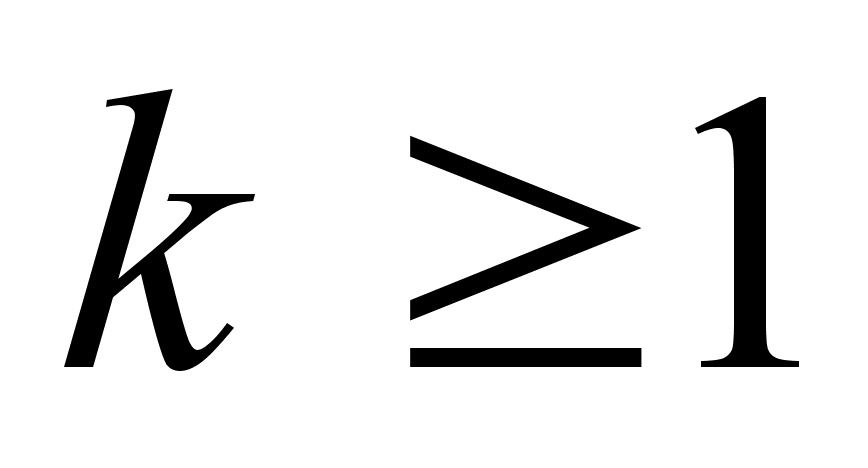 )
)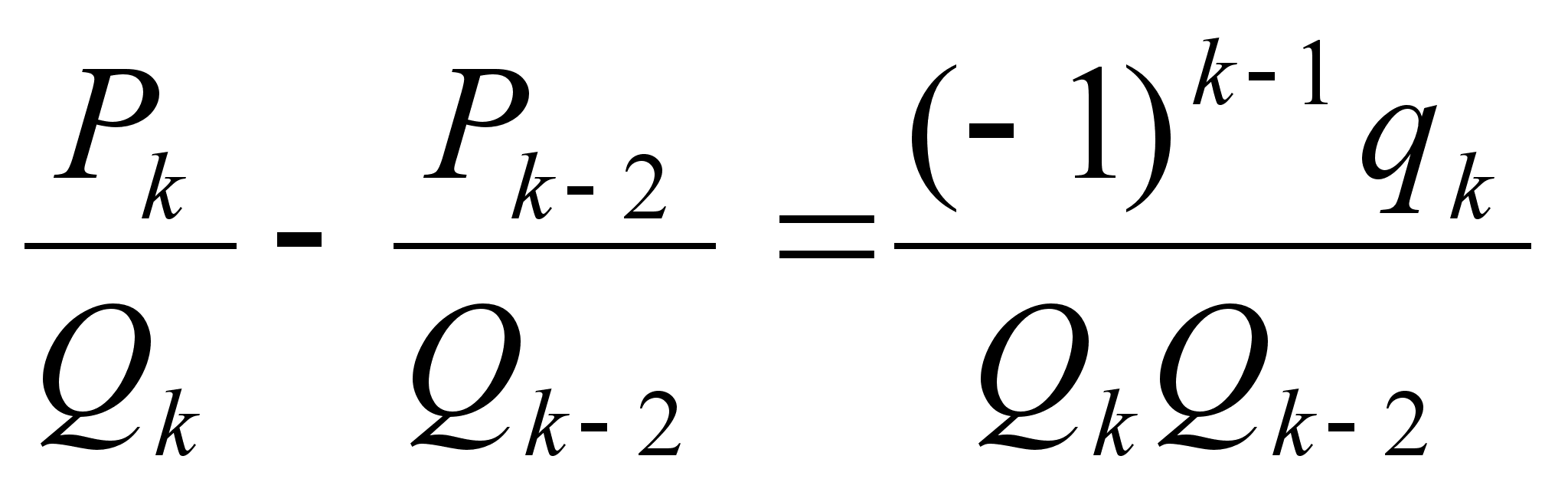 (
(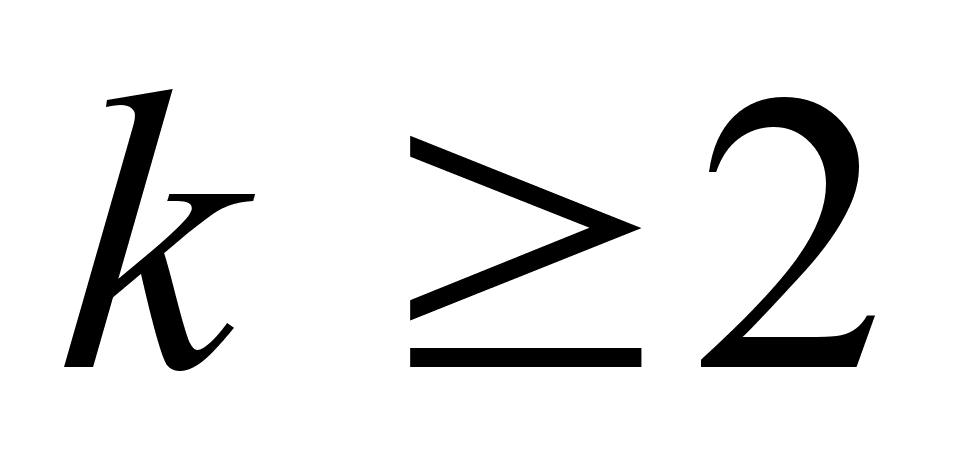 )
)
Доказательство:
Первое соотношение
можно получить
из равенства
![]() ,
доказанного
выше, путем
деления обеих
частей на
,
доказанного
выше, путем
деления обеих
частей на
![]() .
Получаем
.
Получаем
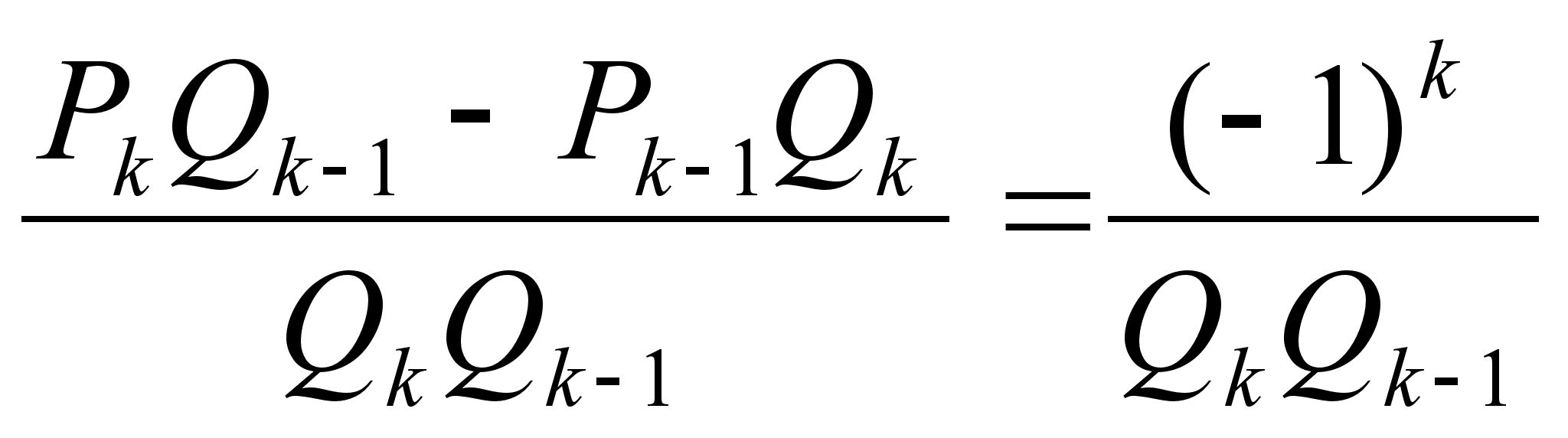
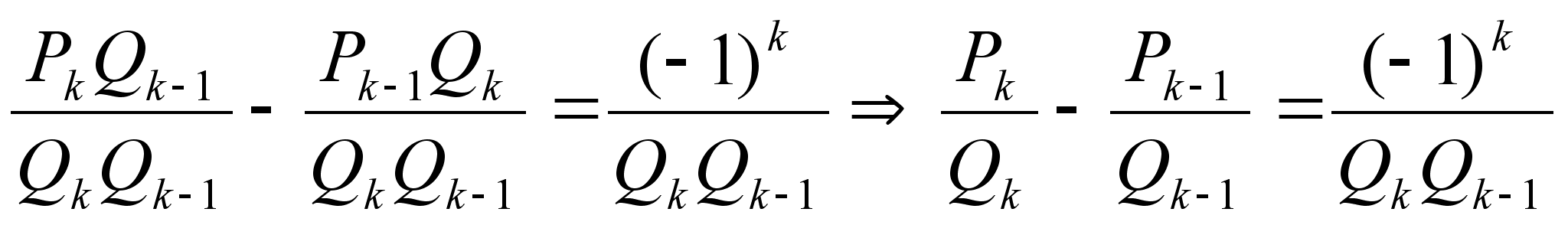 ,
что
и требовалось
доказать.
,
что
и требовалось
доказать.
Докажем второе соотношение.
![]()
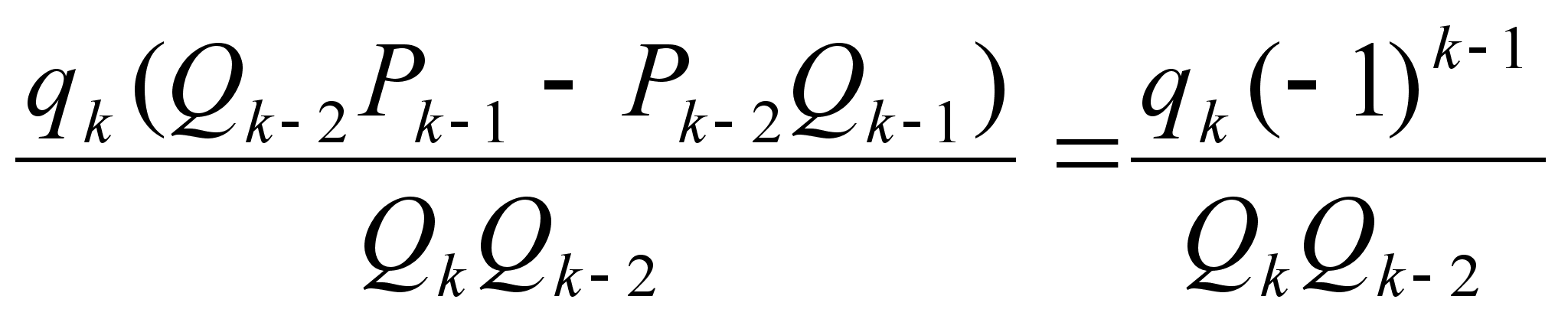 .
.
Теорема доказана полностью.
Теорема: Знаменатели подходящих дробей к цепной дроби, начиная с первого, образуют монотонно возрастающую последовательность, то есть 1=
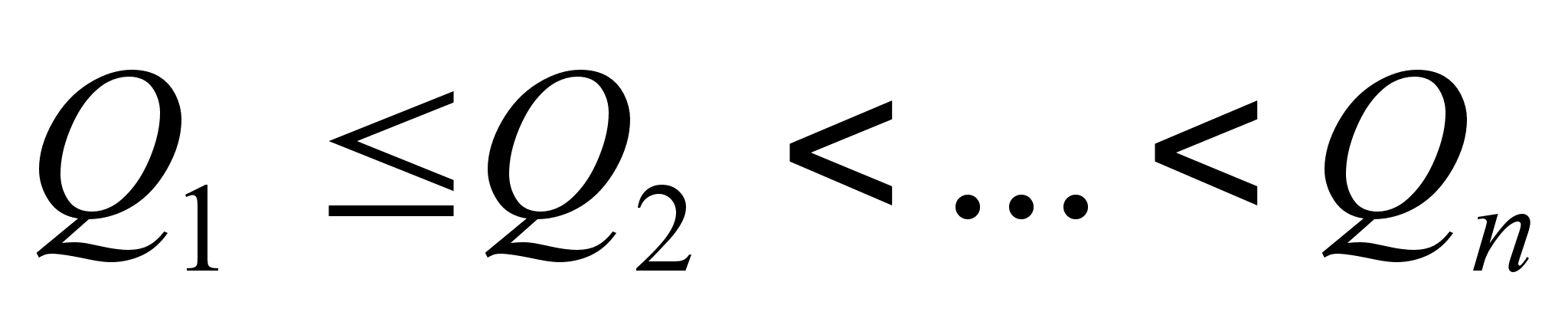 .
.
Доказательство:
![]() ,
,
![]() ,
так что
,
так что
![]() и
и
![]() положительны.
положительны.
Соотношение
![]() (
(![]() )
(*)
показывает,
что и все следующие
знаменатели
)
(*)
показывает,
что и все следующие
знаменатели
![]() ,
,
![]() ,
…,
,
…,
![]() положительны.
При
положительны.
При
![]() ,
поскольку тогда
,
поскольку тогда
![]() ,
из (*)
получаем
,
из (*)
получаем
![]() ,
что и требовалось
доказать.
,
что и требовалось
доказать.
Теорема: Нечетные подходящие дроби образуют возрастающую, а четные подходящие дроби – убывающую последовательность:
![]() ;
;
![]() .
.
Две
подходящие
дроби
![]() и
и
![]() ,
у которых номер
отличается
на единицу,
будем называть
соседними.
,
у которых номер
отличается
на единицу,
будем называть
соседними.
Теорема: Из двух соседних подходящих дробей четная дробь всегда больше нечетной.
Доказательство: По уже доказанному выше свойству имеем:
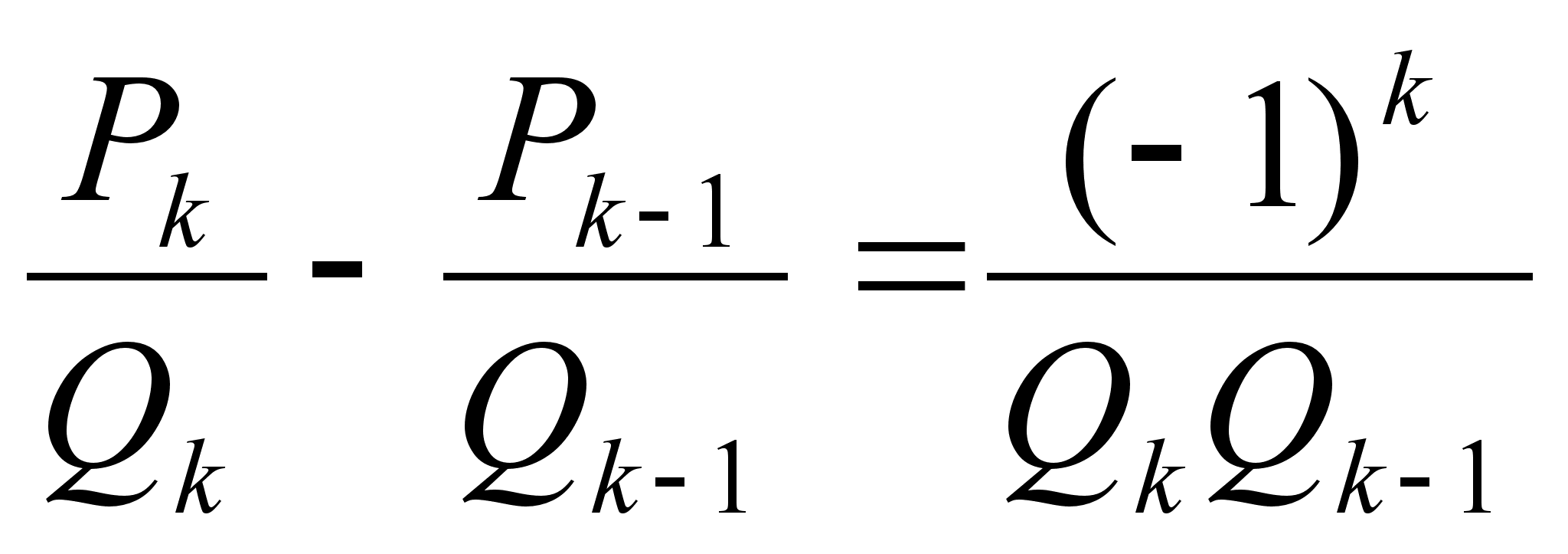 .
.
Если
k
–
четное,
то
![]()
![]()
Если
k
–
нечетное,
то
![]()
![]()
Значит,
из двух соседних
дробей
![]() и
и
![]() четная всегда
больше нечетной,
что и требовалось
доказать.
четная всегда
больше нечетной,
что и требовалось
доказать.
Теорема: Расстояние между двумя соседними подходящими дробями
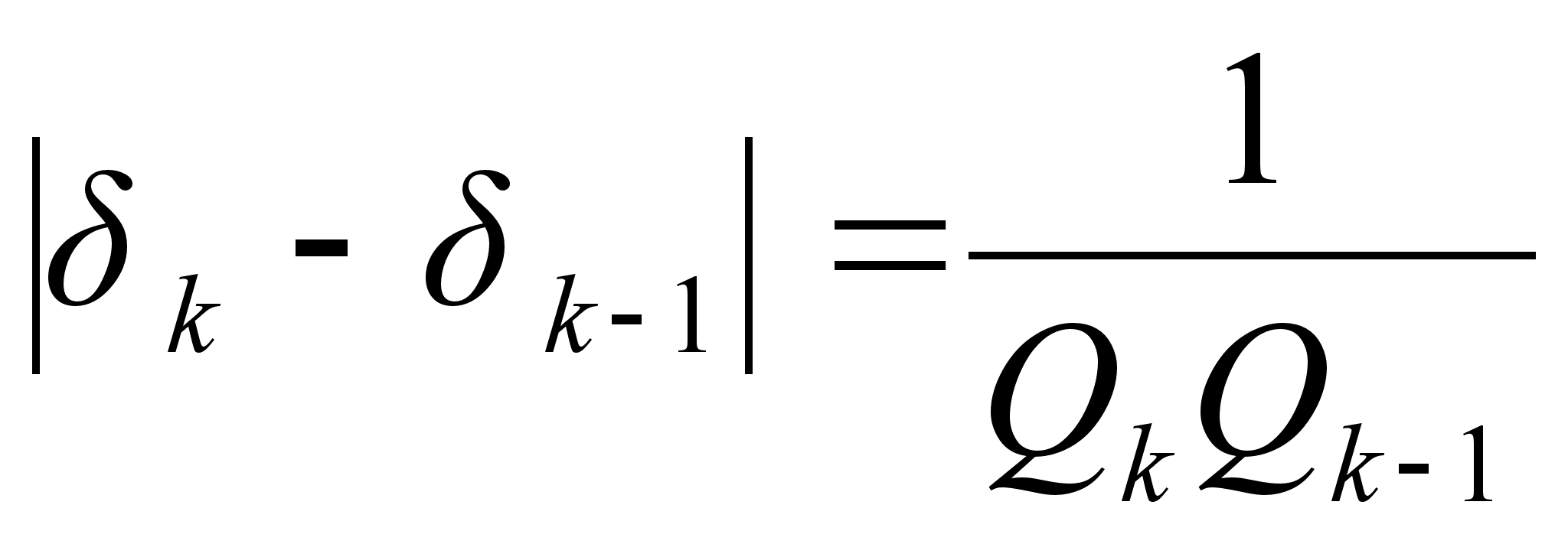 .
.
Доказательство:
Так как
![]() ,
то
,
то
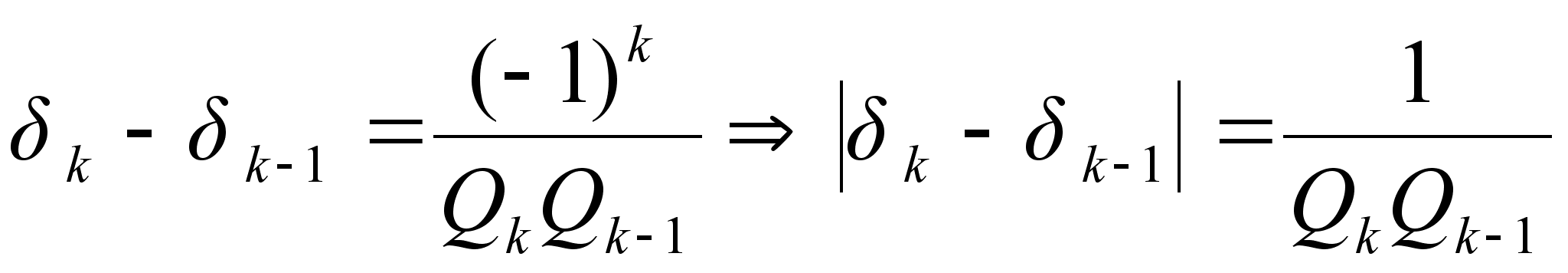 ,
что и требовалось
доказать.
,
что и требовалось
доказать.
Глава II. Бесконечные цепные дроби.
§1. Представление действительных иррациональных чисел правильными бесконечными цепными дробями.
Разложение действительного иррационального числа в правильную бесконечную цепную дробь.
В предыдущей
главе мы рассмотрели,
как в процессе
последовательного
выделения целой
части и перевертывания
дробной рациональная
дробь
![]() разлагается
в конечную
непрерывную
дробь.
разлагается
в конечную
непрерывную
дробь.
![]()
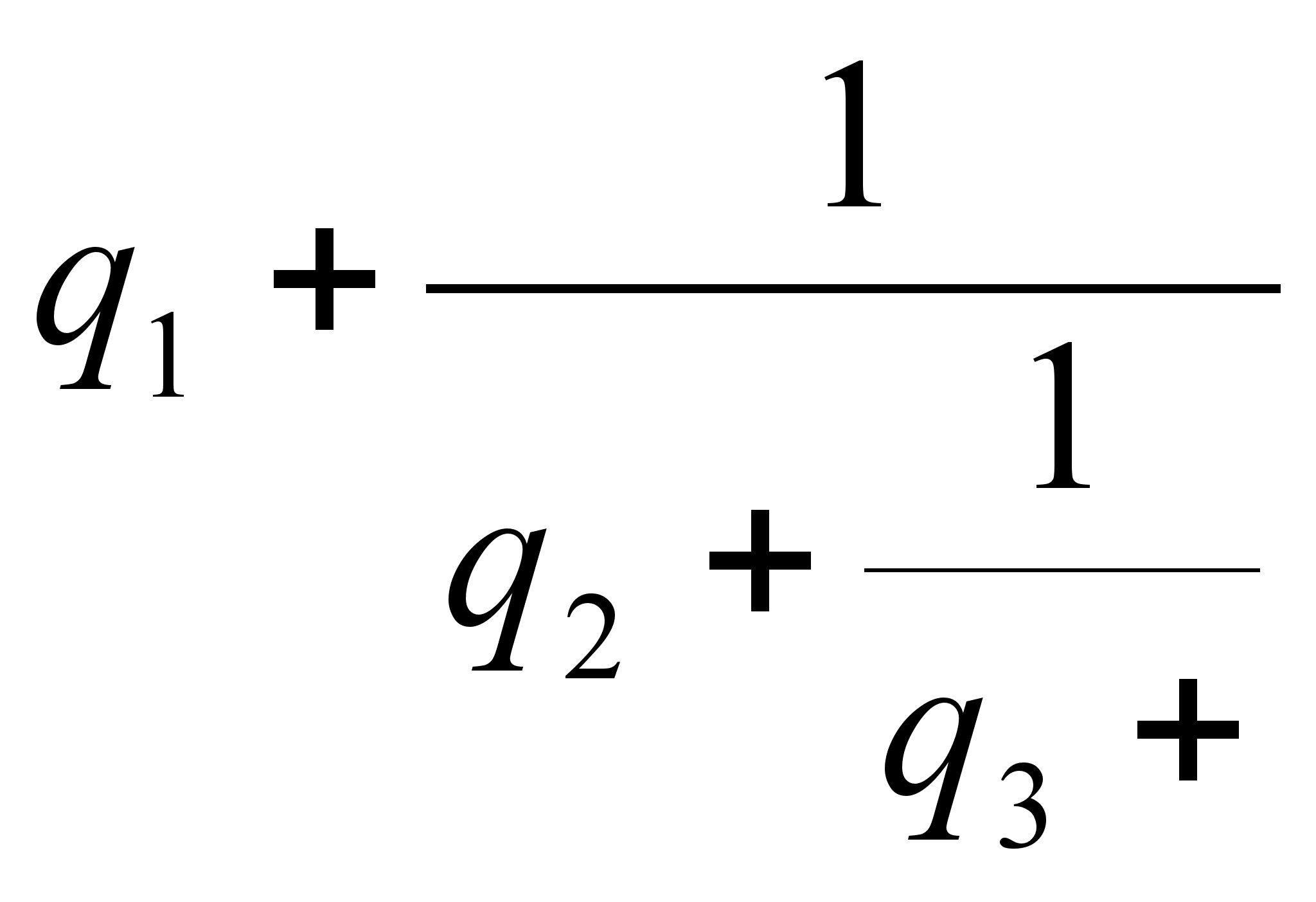 =(
=(![]() )
)
![]() (1)
(1)
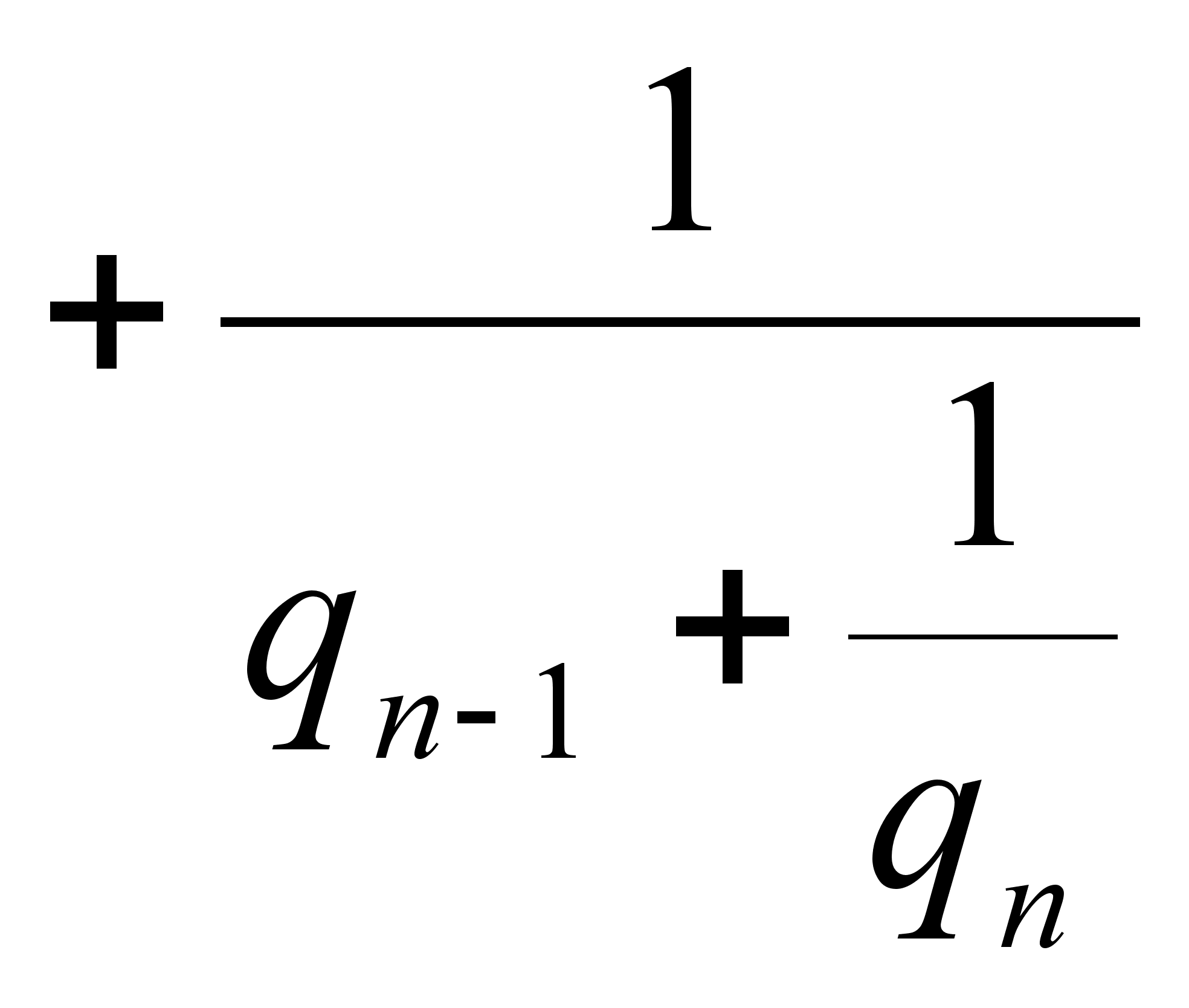
и, наоборот, свертывание такой непрерывной дроби приводит к рациональной дроби.
Процесс выделения целой части и перевертывания дробной можно применить к любому действительному числу.
Для
иррационального
числа
![]() указанный
процесс должен
быть бесконечным,
так как конечная
цепная дробь
равна рациональному
числу.
указанный
процесс должен
быть бесконечным,
так как конечная
цепная дробь
равна рациональному
числу.
Выражение
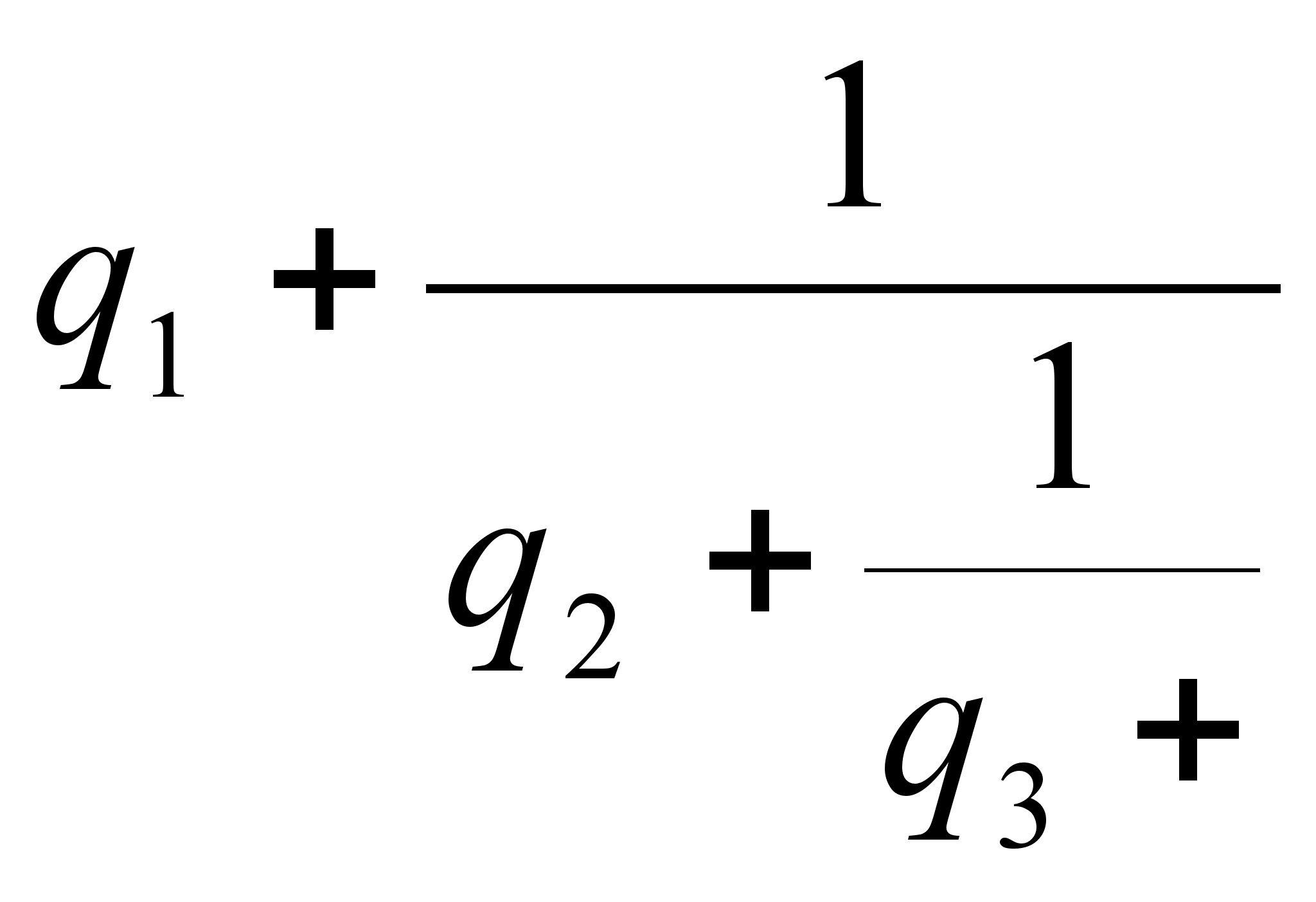 (где
(где
![]() ,
,
![]() )
(2)
)
(2)
![]()
возникающее
в таком процессе
или заданное
формально, мы
будем называть
правильной
бесконечной
цепной,
или непрерывной
дробью,
или дробью
бесконечной
длины
и обозначать
кратко через
(![]() ),
а числа
),
а числа
![]() – ее
элементами
или неполными
частными.
– ее
элементами
или неполными
частными.
Отметим,
что разложение
![]() возможно только
в единственном
виде, так как
процесс выделения
целой части
– процесс
однозначный.
возможно только
в единственном
виде, так как
процесс выделения
целой части
– процесс
однозначный.
Рассмотрим
пример разложения
иррационального
числа
![]() .
.
Пусть
![]() .
Выделим из
.
Выделим из
![]() его целую часть.
его целую часть.
![]() =3,
а дробную часть
=3,
а дробную часть
![]() –3,
которая меньше
1, представим
в виде
–3,
которая меньше
1, представим
в виде
![]() ,
где
,
где
![]() .
.
Повторяя операцию выделения целой части и перевертывания дробной, мы получаем:
![]() ;
;
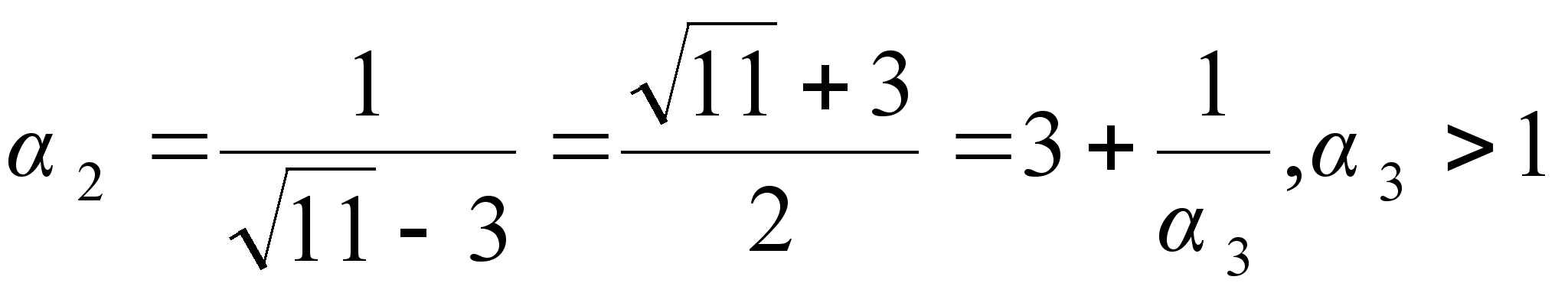 ;
;
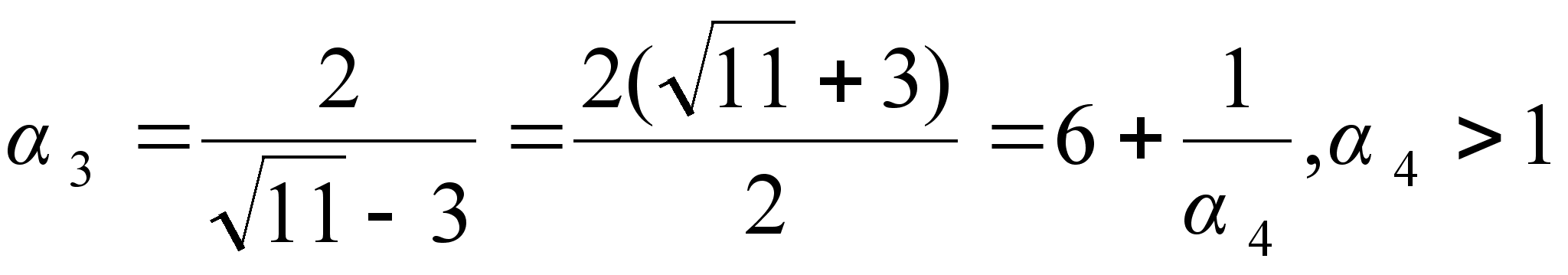 .
.
Если остановиться на этом шаге, то можно записать:
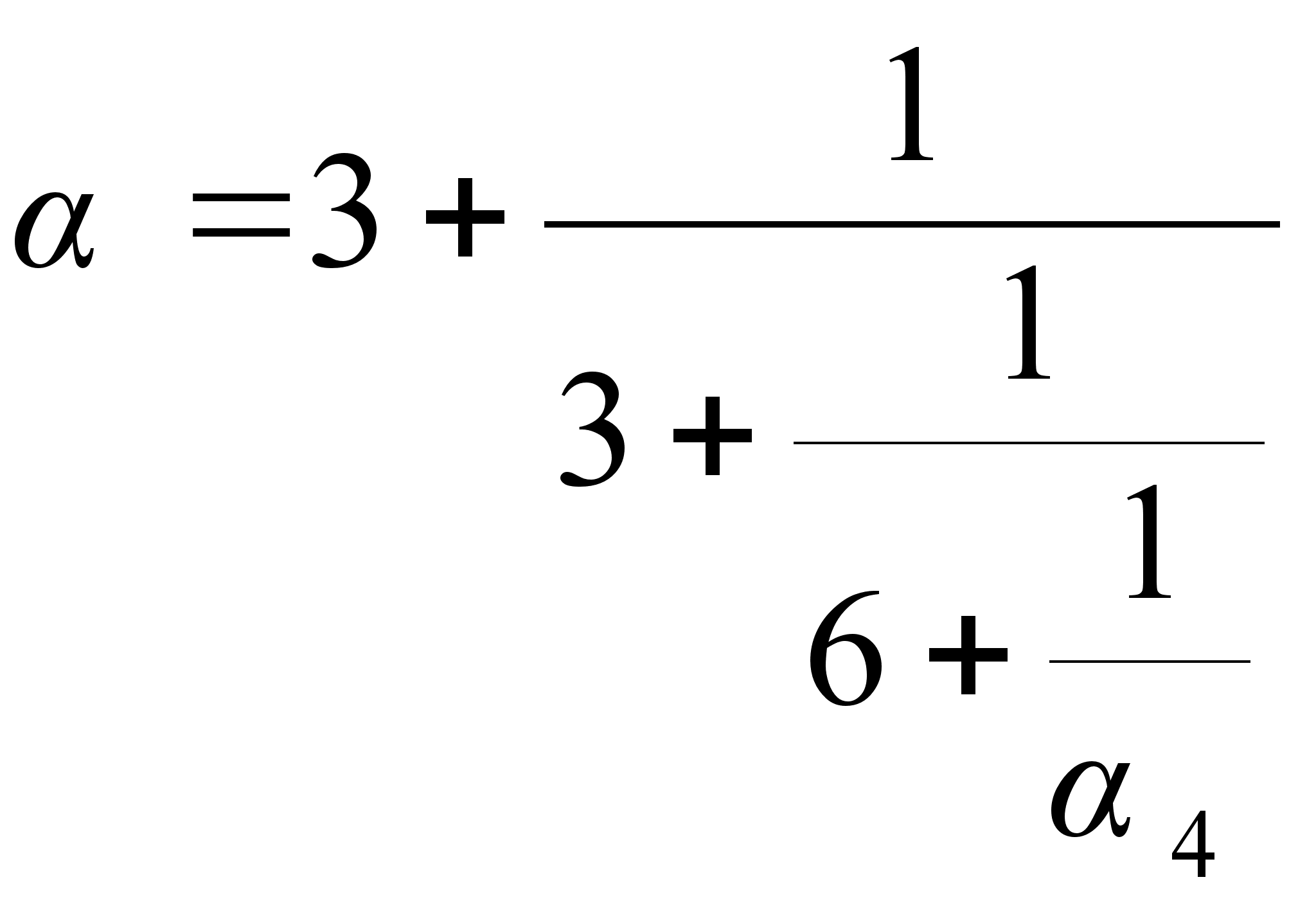
С другой
стороны, из
формулы для
![]() видно, что
видно, что
![]() =3+
=3+![]() .
Поэтому
.
Поэтому
![]() ,
вследствие
чего, начиная
с этого момента,
неполные частные
станут повторяться.
,
вследствие
чего, начиная
с этого момента,
неполные частные
станут повторяться.
Бесконечная непрерывная дробь, в которой определенная последовательность неполных частных, начиная с некоторого места, периодически повторяется, называется периодической непрерывной дробью.
Если, в частности, периодическое повторение начинается с первого звена, то цепная дробь называется чисто периодической, в противном случае – смешанной периодической.
Чисто
периодическая
дробь
![]() записывается
в виде
записывается
в виде
![]() ,
а смешанная
периодическая
,
а смешанная
периодическая
![]() в виде
в виде
![]() .
.
Итак,
![]() разлагается
в смешанную
периодическую
дробь (3, 3, 6, 3, 6, …) или
(3, (3, 6)).
разлагается
в смешанную
периодическую
дробь (3, 3, 6, 3, 6, …) или
(3, (3, 6)).
В общем
случае разложения
действительного
иррационального
числа
![]() поступаем так
же, как в примере.
Останавливаясь
при этом в процессе
выделения целой
части после
k–го
шага, будем
иметь:
поступаем так
же, как в примере.
Останавливаясь
при этом в процессе
выделения целой
части после
k–го
шага, будем
иметь:
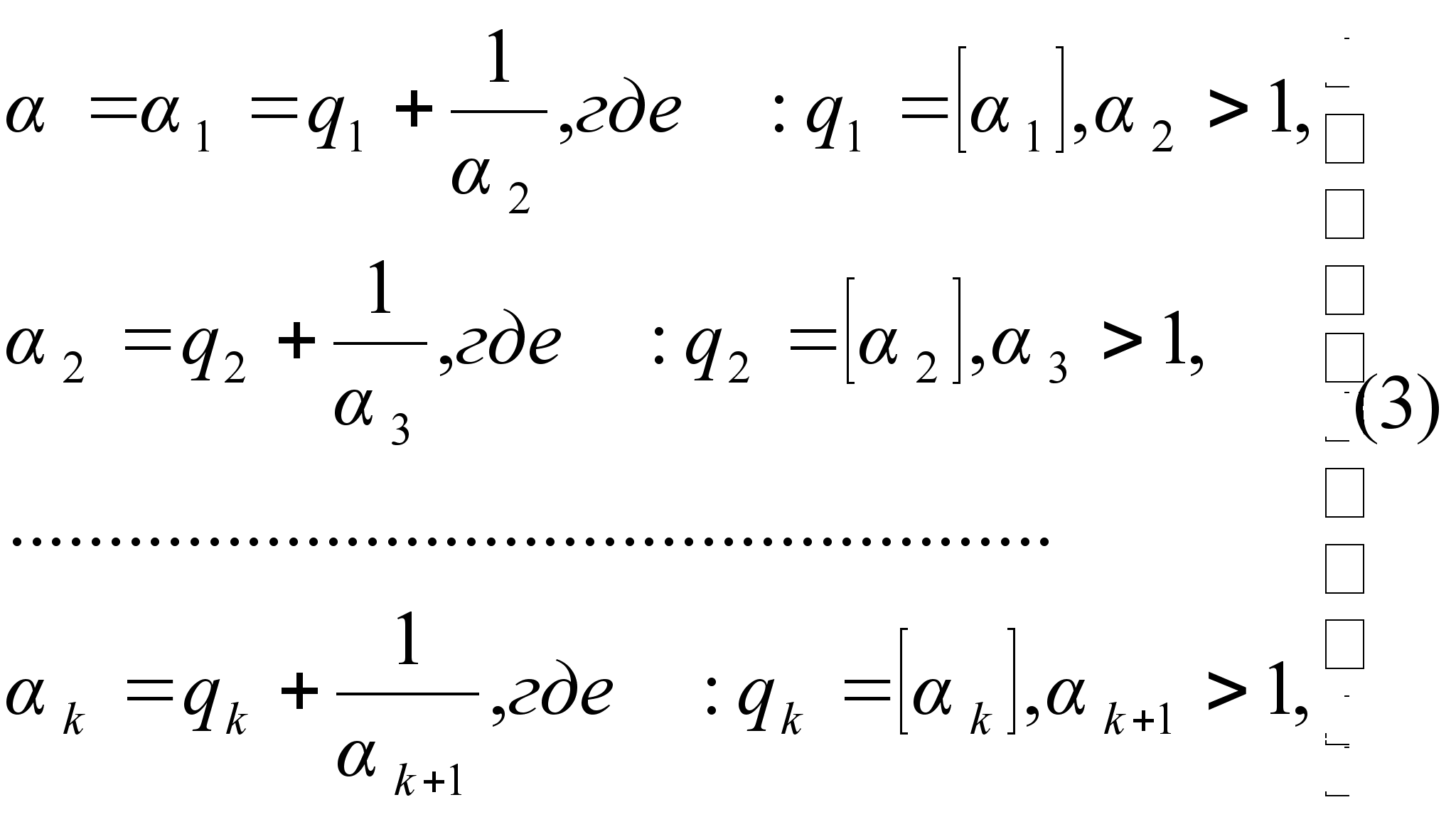
так что
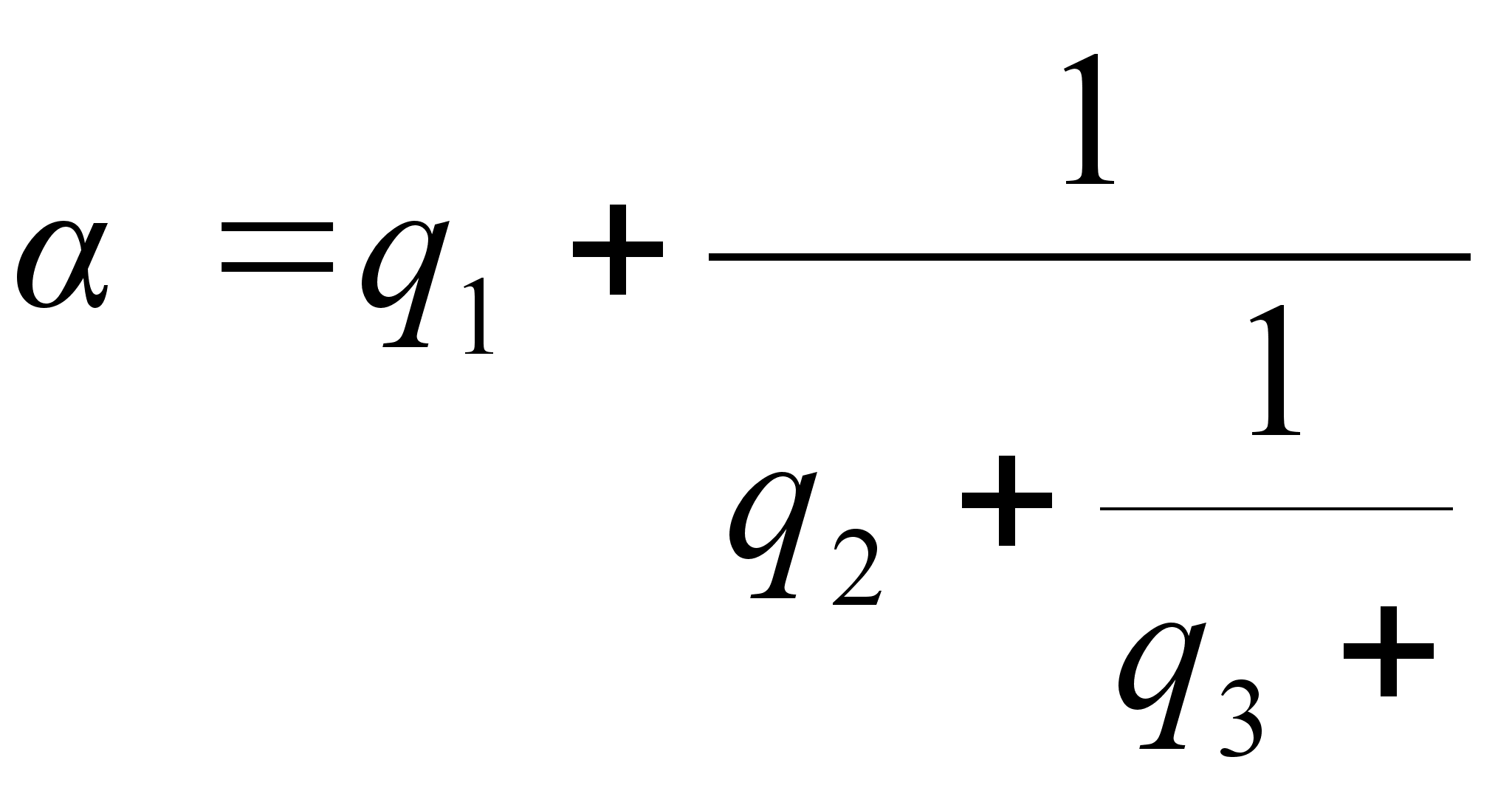
![]()
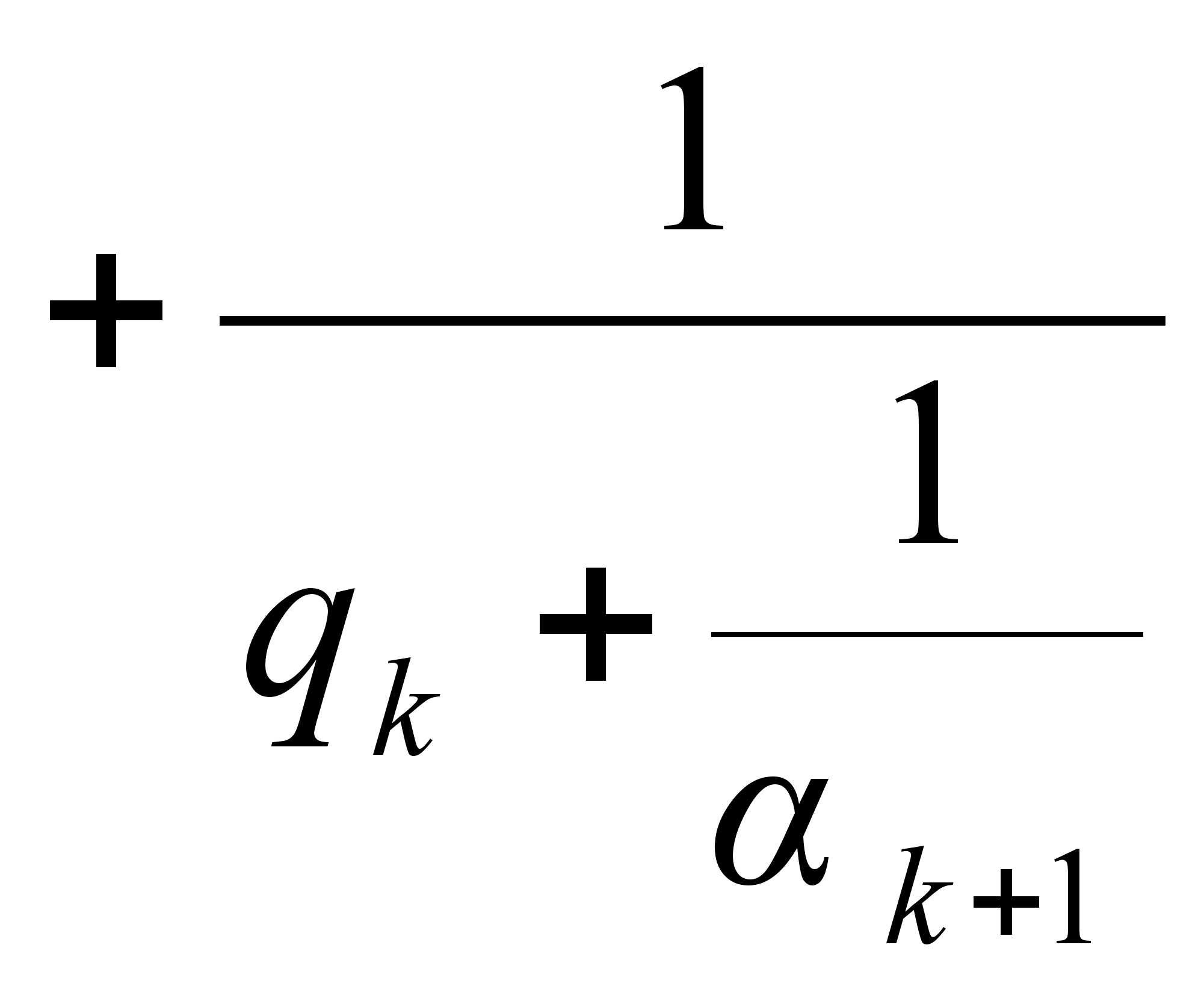 .
.
Числа
![]() называются
остаточными
числами порядка
k
разложения
называются
остаточными
числами порядка
k
разложения
![]() .
В формуле (4) имеем
кусок разложения
до остаточного
числа
.
В формуле (4) имеем
кусок разложения
до остаточного
числа
![]() .
.
Для бесконечной цепной дроби (2) можно построить бесконечную последовательность конечных непрерывных дробей.
![]()
Эти дроби
называют подходящими
дробями.
Закон образования
соответствующих
им простых
дробей будет
такой же, как
и для подходящих
дробей в случае
конечных непрерывных
дробей, так как
этот закон
зависит только
от неполных
частных
![]() и совершенно
не зависит от
того, является
ли
и совершенно
не зависит от
того, является
ли
![]() последним
элементом или
за ним следует
еще элемент
последним
элементом или
за ним следует
еще элемент
![]() .
Поэтому для
них сохранятся
также остальные
свойства, которые
выводятся из
закона образования
числителей
и знаменателей
подходящих
дробей.
.
Поэтому для
них сохранятся
также остальные
свойства, которые
выводятся из
закона образования
числителей
и знаменателей
подходящих
дробей.
В частности, мы имеем:
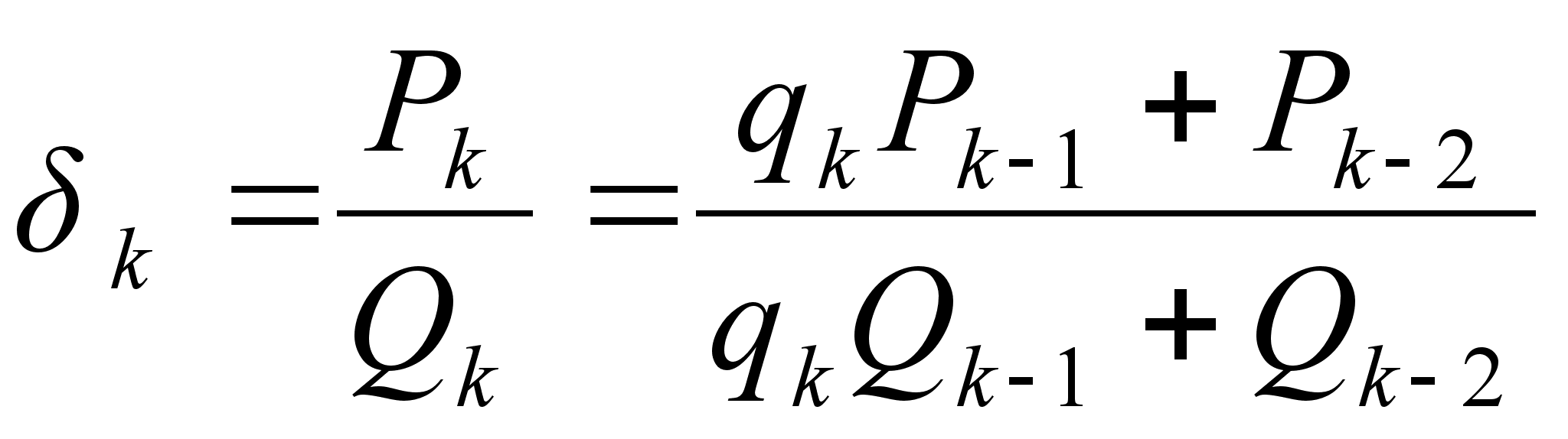 ,
причем
,
причем
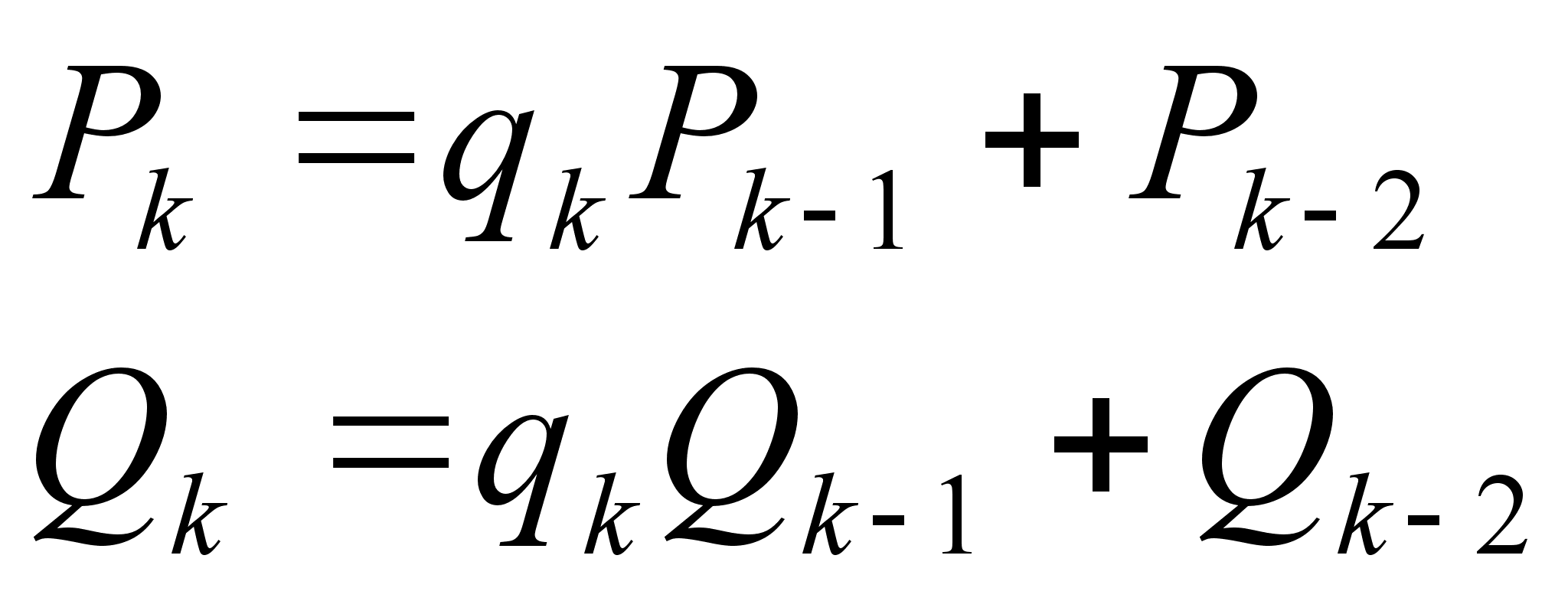 ;
;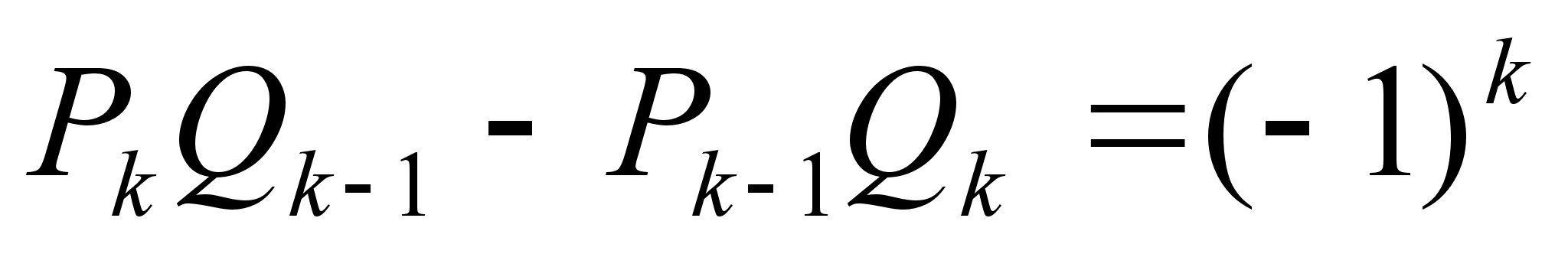 ,
откуда следует
несократимость
подходящих
дробей
,
откуда следует
несократимость
подходящих
дробей
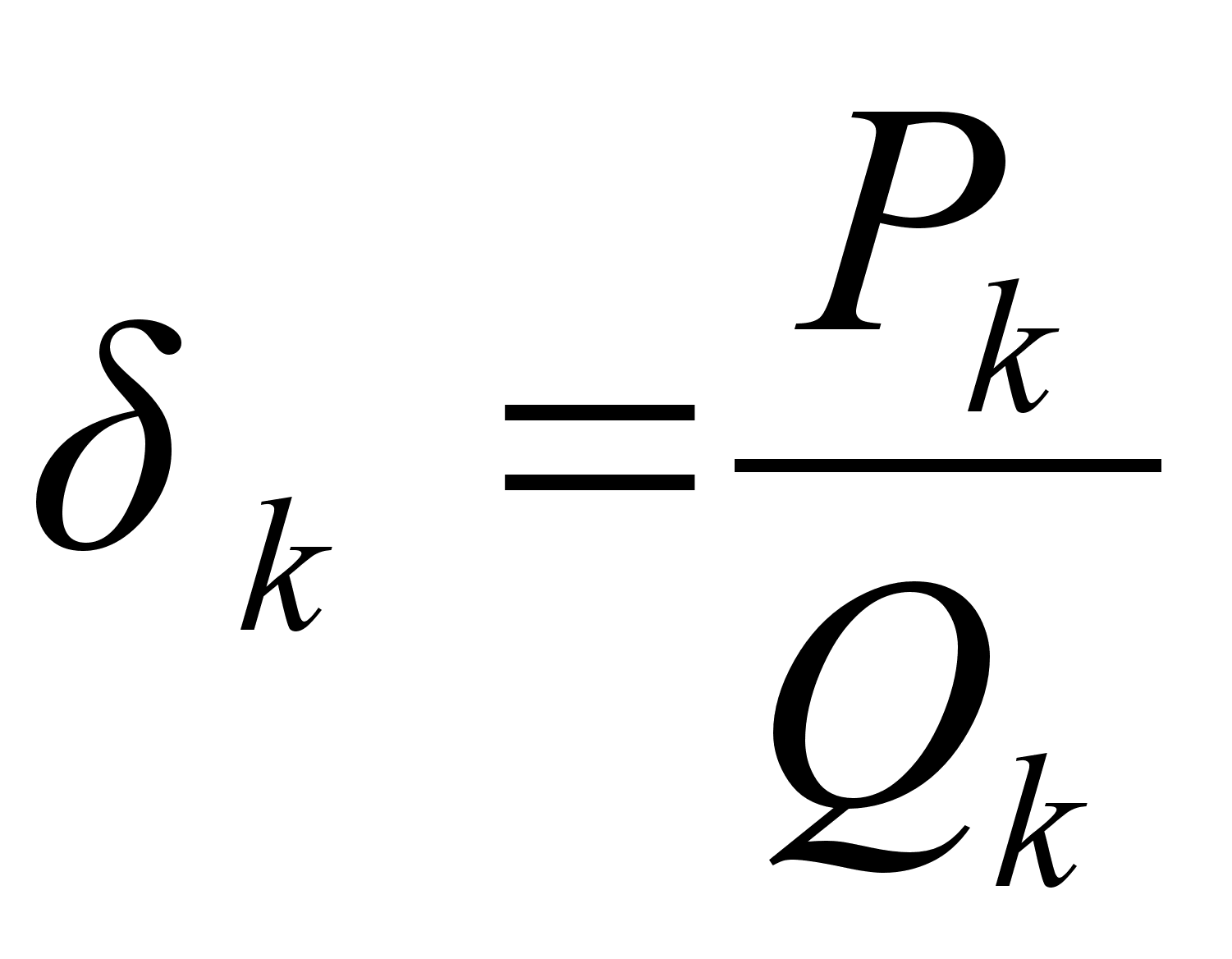 ;
;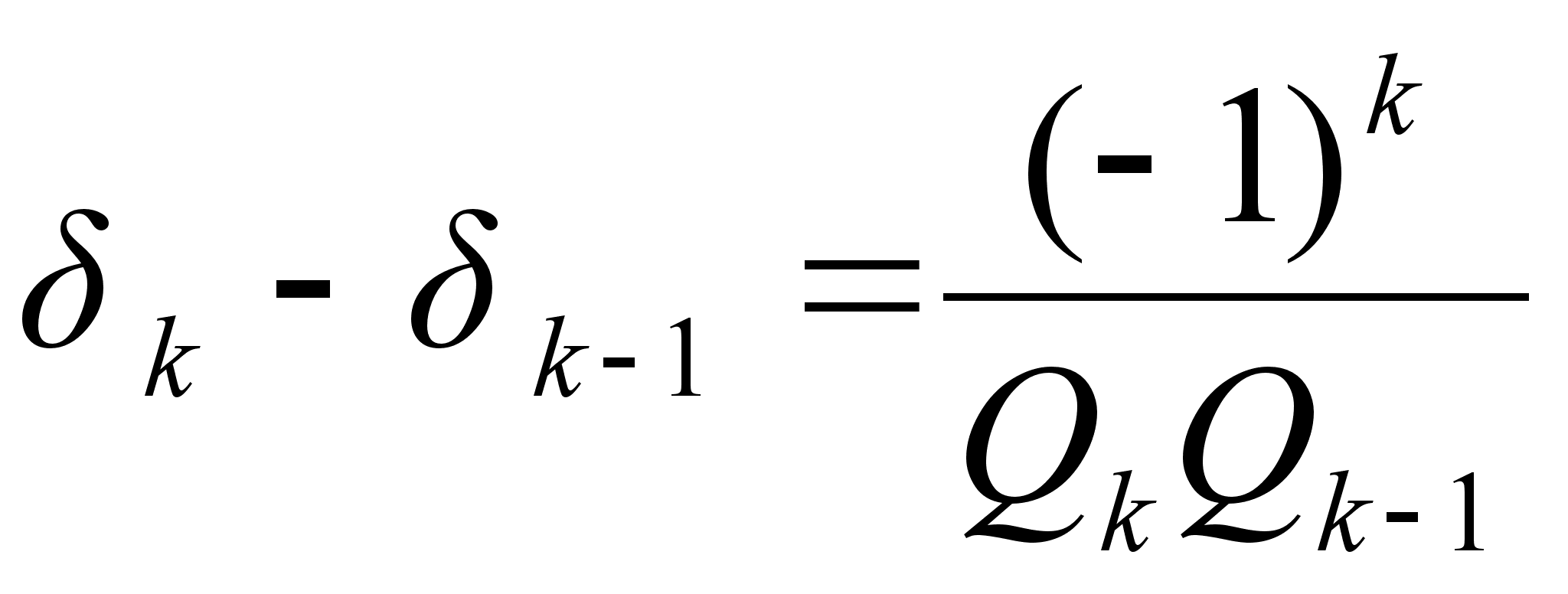 .
.
Сравним
теперь подходящую
дробь
![]() и кусок разложения
и кусок разложения
![]() до остаточного
числа
до остаточного
числа
![]() .
Имеем
.
Имеем
![]()
![]()
![]()
![]()
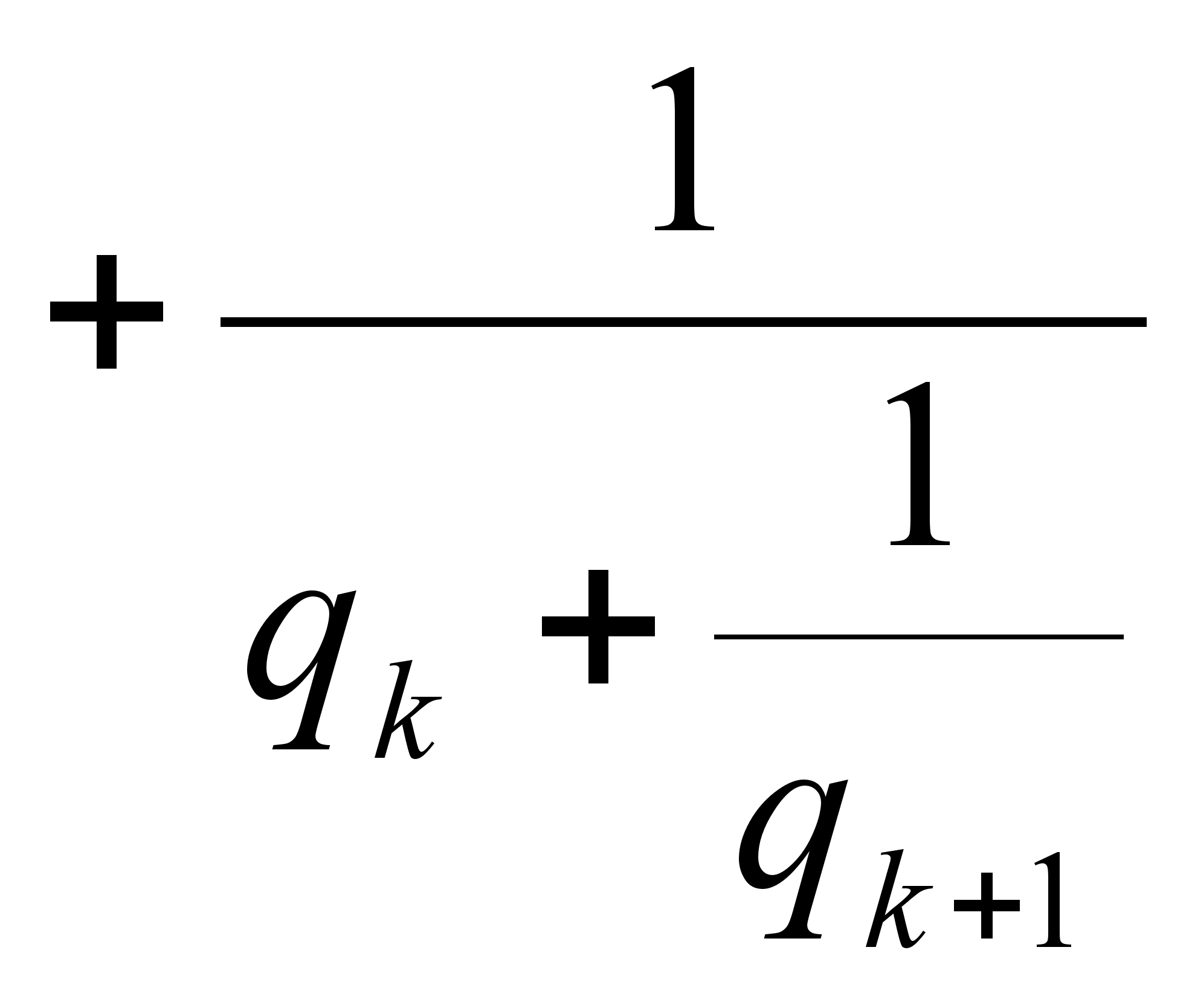
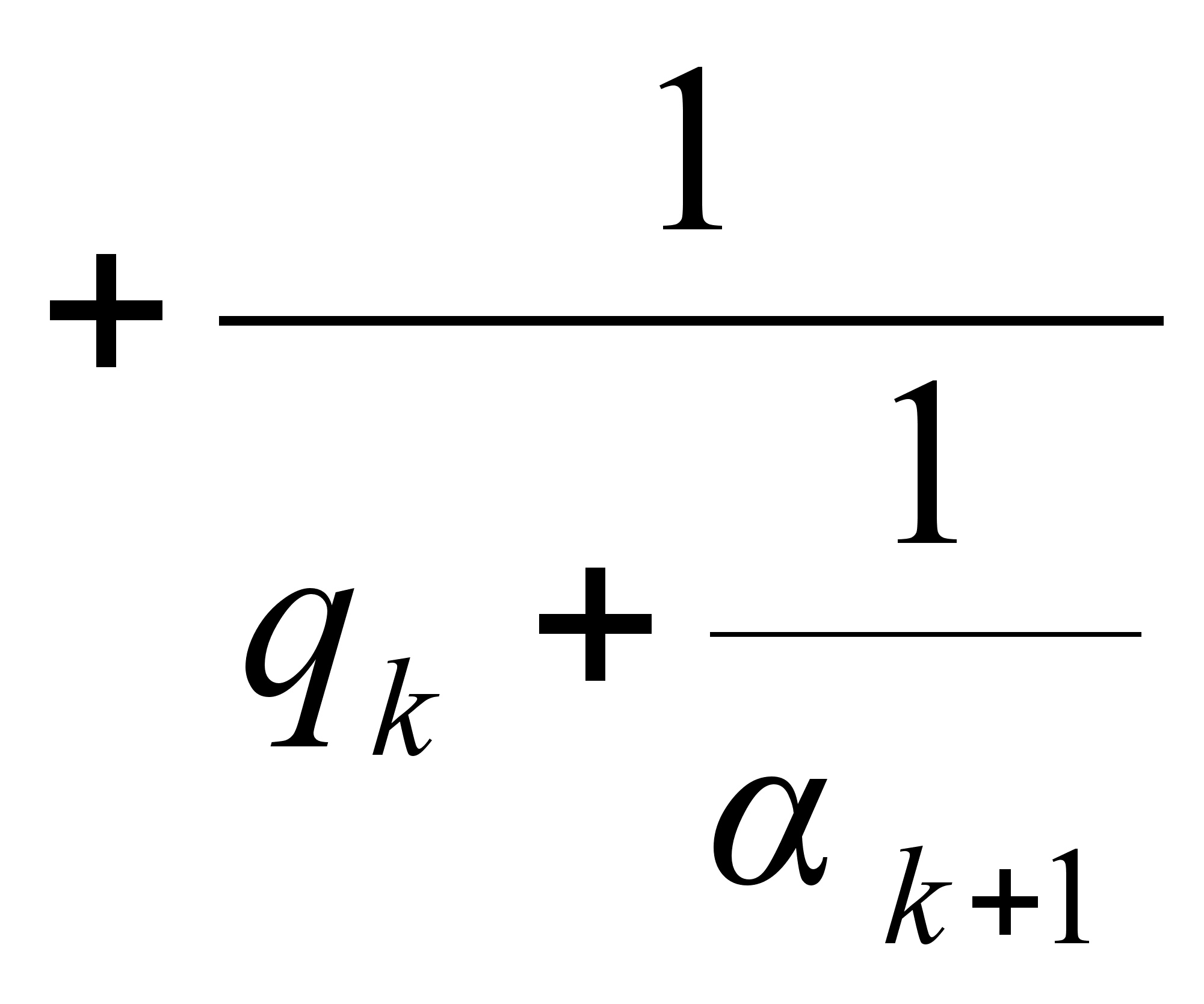 ,
,
откуда
видно, что вычисление
![]() по
по
![]() формально
производится
таким же образом,
как вычисление
формально
производится
таким же образом,
как вычисление
![]() по
по
![]() с тем лишь отличием,
что в первом
случае
с тем лишь отличием,
что в первом
случае
![]() заменяется
на
заменяется
на
![]() ,
а во втором
,
а во втором
![]() заменяется
на
заменяется
на
![]() .
Поэтому на
основании
формулы
.
Поэтому на
основании
формулы
![]() можно сделать
вывод о справедливости
следующего
важного соотношения
можно сделать
вывод о справедливости
следующего
важного соотношения
![]() .
(5)
.
(5)
По
этой причине
мы пишем также
![]() ,
хотя
,
хотя
![]() не является
здесь целым
положительным
числом.
не является
здесь целым
положительным
числом.
При помощи
формулы (5) можно
вывести следующую
теорему и
расположении
подходящих
дробей разложения
![]() .
.
Теорема:
Действительное
число
![]() всегда находится
между двумя
соседними
подходящими
дробями своего
разложения,
причем оно
ближе к последующей,
чем к предыдущей
подходящей
дроби.
всегда находится
между двумя
соседними
подходящими
дробями своего
разложения,
причем оно
ближе к последующей,
чем к предыдущей
подходящей
дроби.
Доказательство: Из формулы (5) следует
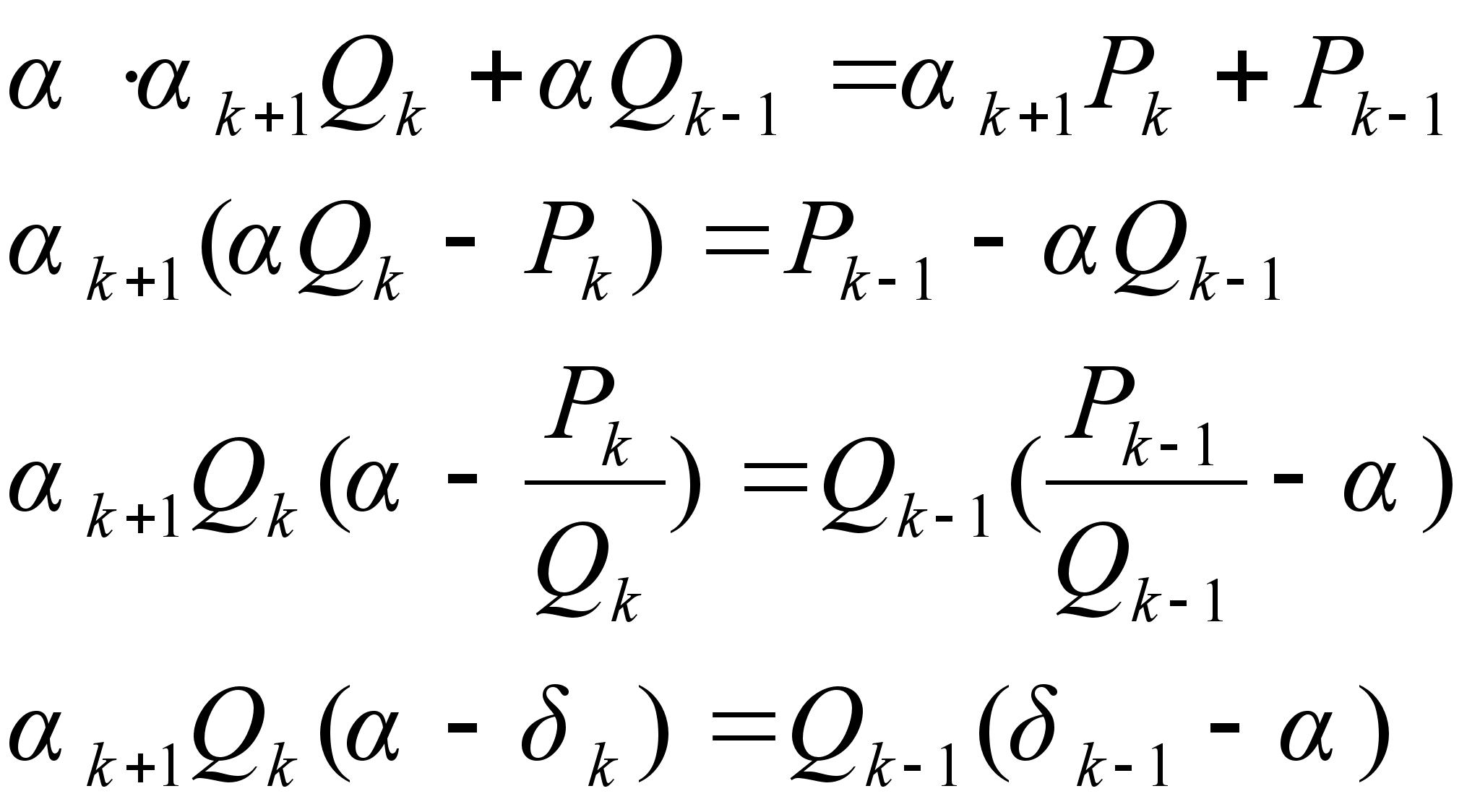
Но
![]() ,
,
![]() ,
так что
,
так что
![]()
(
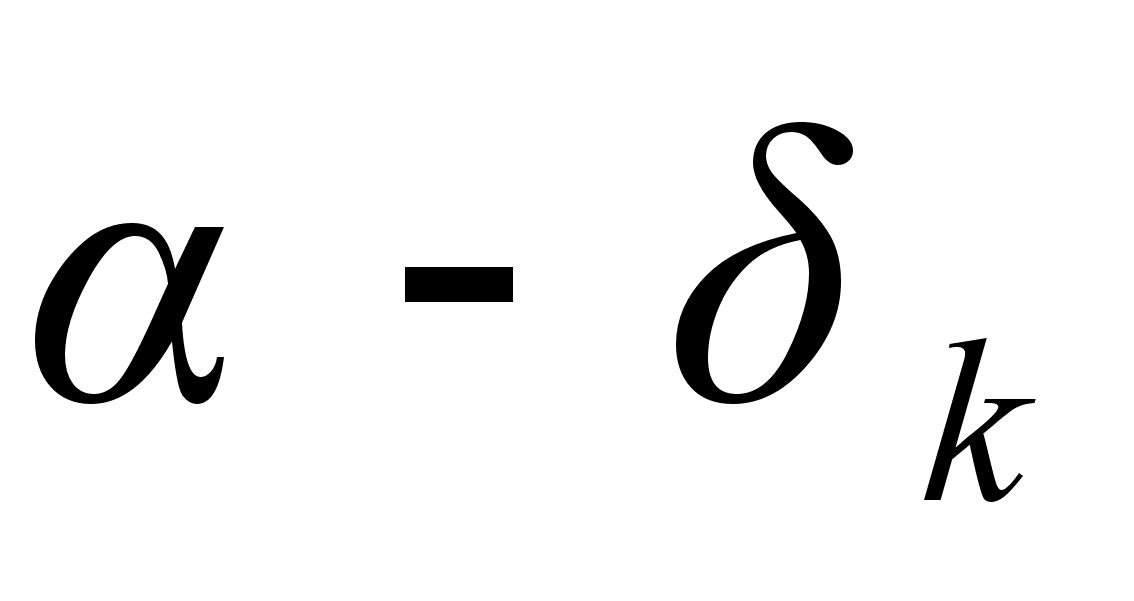 )
и (
)
и (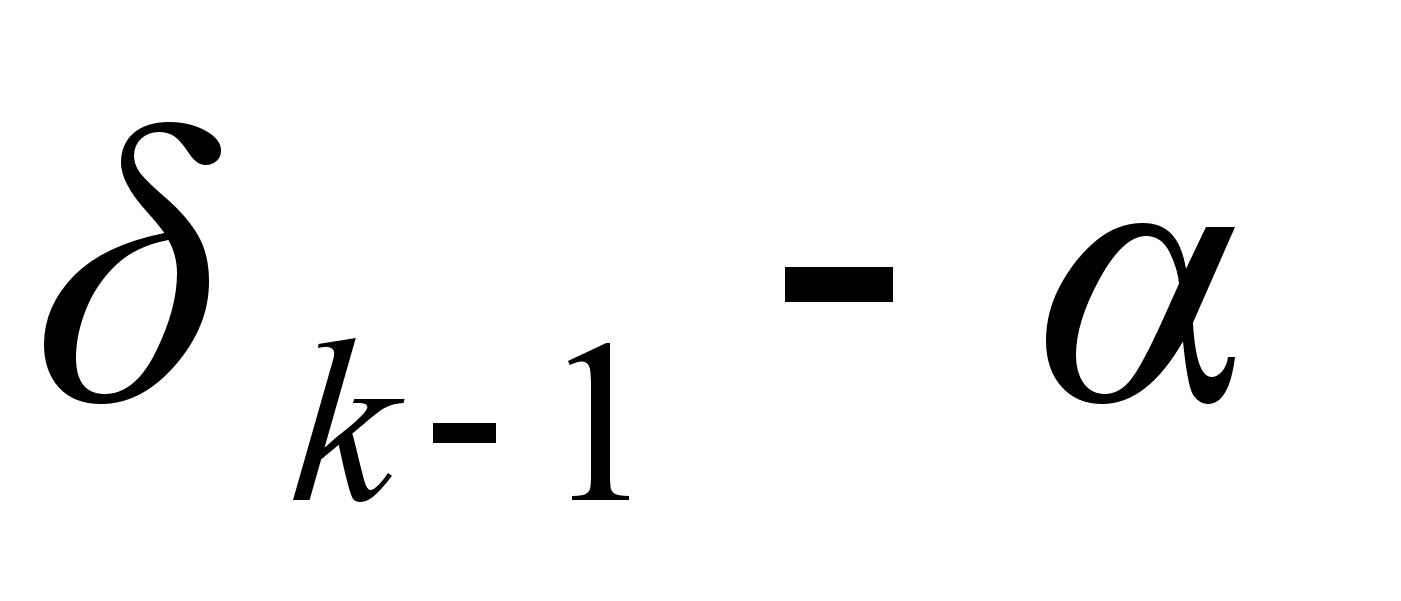 )
имеют одинаковый
знак, а это значит,
что
)
имеют одинаковый
знак, а это значит,
что
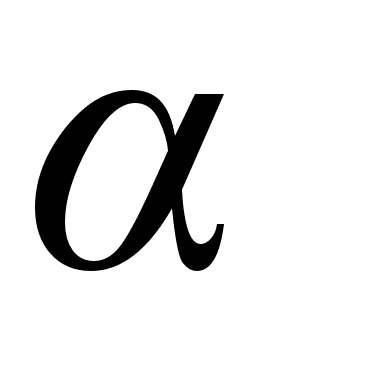 находится
между
находится
между
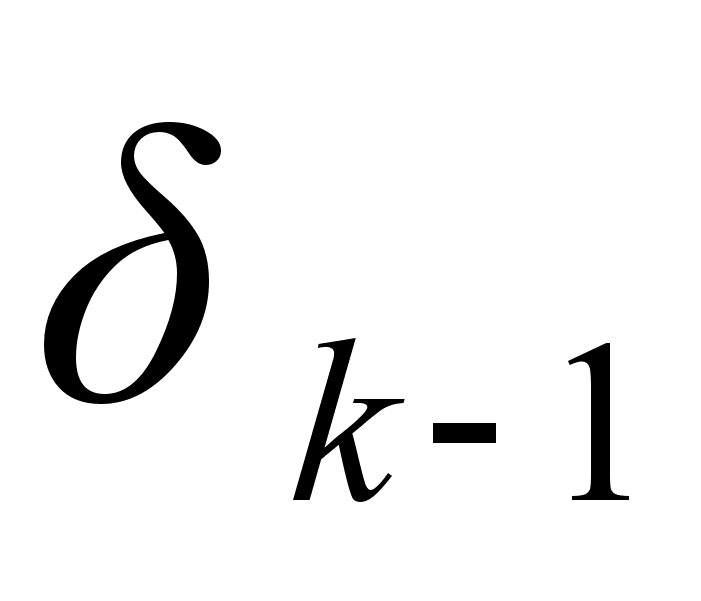 и
и
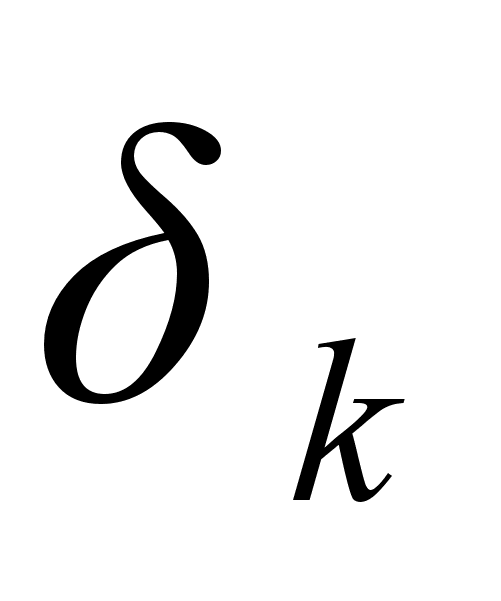 ;
;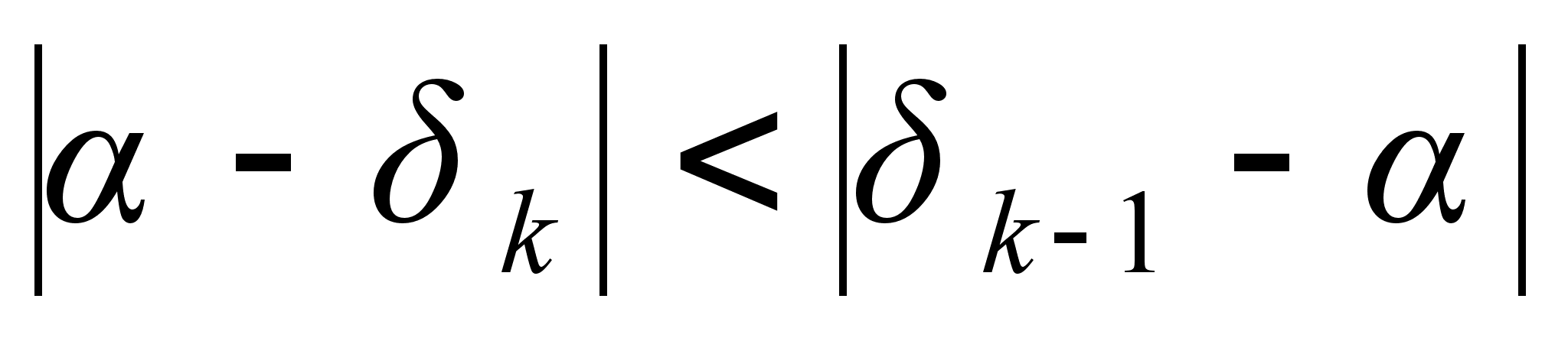 ,
то есть
,
то есть
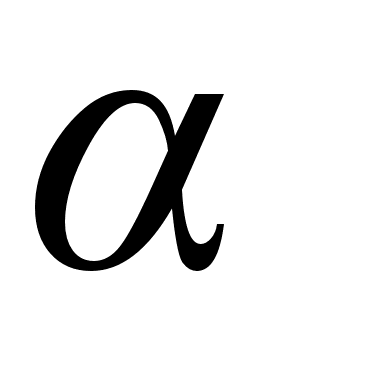 ближе к
ближе к
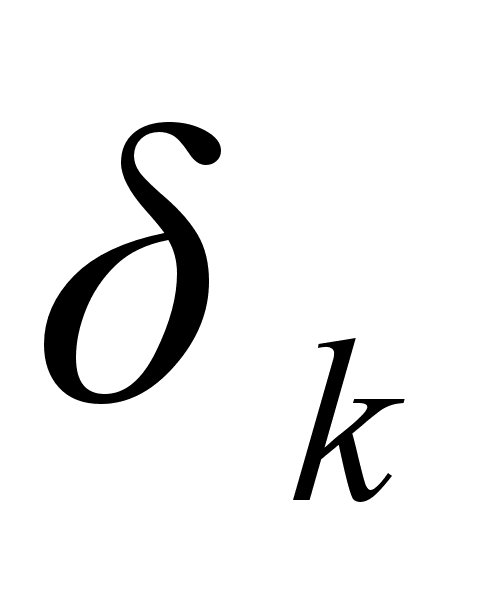 ,
чем к
,
чем к
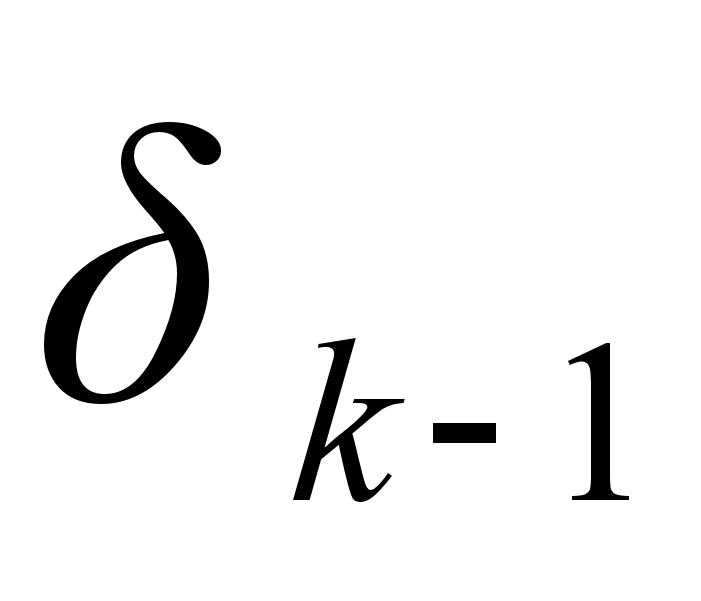 .
.
Теорема доказана.
Так как
![]() ,
то
,
то
![]() ,
и так далее;
отсюда приходим
к следующему
заключению
о взаимном
расположении
подходящих
дробей:
,
и так далее;
отсюда приходим
к следующему
заключению
о взаимном
расположении
подходящих
дробей:
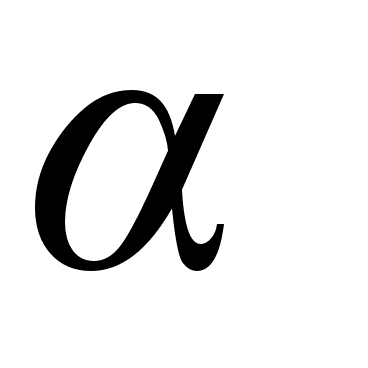 больше
всех подходящих
дробей нечетного
порядка и меньше
всех подходящих
дробей четного
порядка;
больше
всех подходящих
дробей нечетного
порядка и меньше
всех подходящих
дробей четного
порядка;подходящие дроби нечетного порядка образуют возрастающую последовательность, а четного порядка – убывающую (в случае иррационального
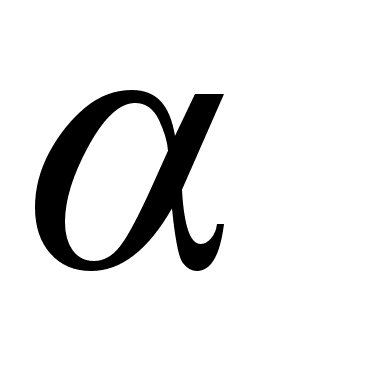
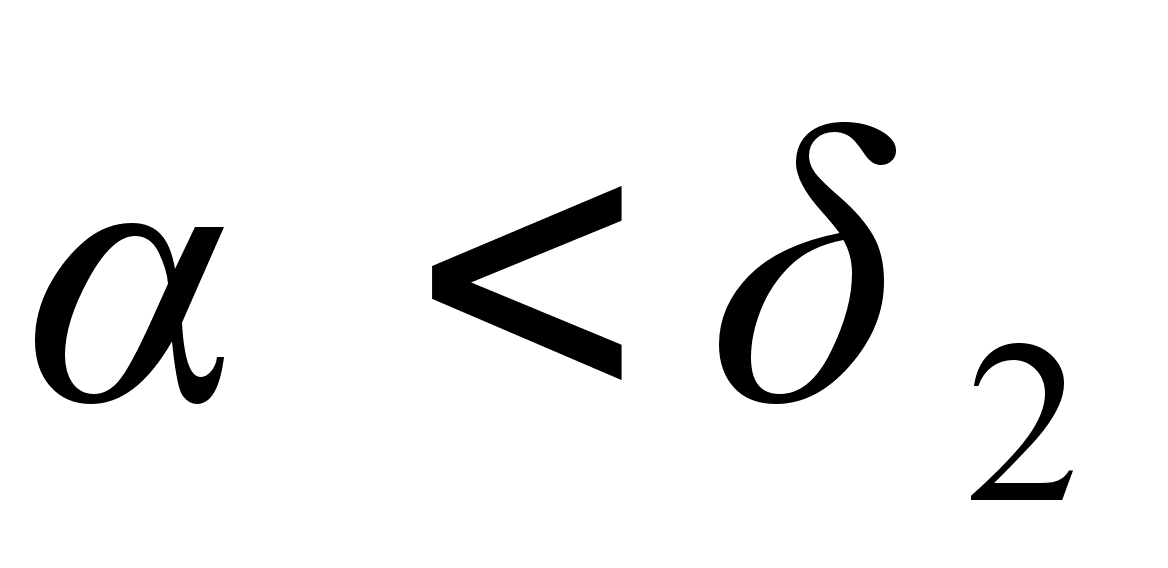
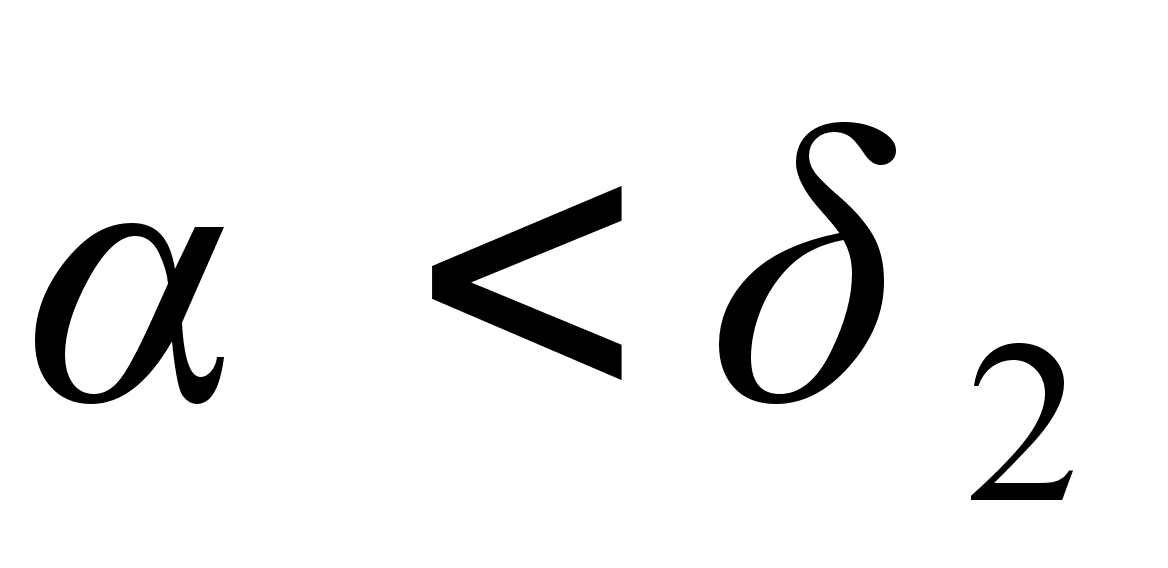
указанные последовательности являются бесконечными), то есть
![]()
(в
случае рационального
![]()
![]() ).
).
————![]() ——
——![]() ————
————![]() ——
——![]() ———
———![]() ————
————
![]()
![]()
![]()
![]()
![]()
Учитывая
то, что при
![]()
![]() ,
вследствие
чего
,
вследствие
чего
![]() ,
переходим к
дальнейшему
выводу, что в
случае иррационального
,
переходим к
дальнейшему
выводу, что в
случае иррационального
![]() сегменты
сегменты
![]() ,
,
![]() ,
… образуют
стягивающуюся
последовательность,
которая, как
известно, должна
иметь единственную
общую точку,
являющуюся
общим пределом
последовательностей
,
… образуют
стягивающуюся
последовательность,
которая, как
известно, должна
иметь единственную
общую точку,
являющуюся
общим пределом
последовательностей
![]() ,
,
![]() ,
… и
,
… и
![]() ,
,
![]() ,
… . Но так как
,
… . Но так как
![]() принадлежит
всем сегментам
последовательности,
то
принадлежит
всем сегментам
последовательности,
то
![]() и совпадает
с указанной
точкой, так что
и совпадает
с указанной
точкой, так что
![]() .
.
Итак, мы имеем следующий важный результат:
бесконечная
последовательность
подходящих
дробей
![]() ,
которая возникает
при разложении
иррационального
,
которая возникает
при разложении
иррационального
![]() ,
сходится к
,
сходится к
![]() ,
колеблясь около
него. Или: иррациональное
действительное
,
колеблясь около
него. Или: иррациональное
действительное
![]() равно пределу
последовательности
подходящих
дробей своего
разложения
в бесконечную
непрерывную
дробь (процессом
выделения целой
части).
равно пределу
последовательности
подходящих
дробей своего
разложения
в бесконечную
непрерывную
дробь (процессом
выделения целой
части).
Сходимость правильных бесконечных цепных дробей.
Теперь
покажем, что
сходящейся
является
последовательность
подходящих
дробей не только
такой бесконечной
непрерывной
дроби, которая
возникает при
разложении
иррационального
числа
![]() ,
но и любой
бесконечной
непрерывной
дроби
,
но и любой
бесконечной
непрерывной
дроби
![]() ,
где
,
где
![]() ,
а
,
а
![]() - произвольно
выбранные целые
положительные
числа.
- произвольно
выбранные целые
положительные
числа.
Но для этого мы заново исследуем взаимное расположение подходящих дробей.
С этой целью рассмотрим формулы:
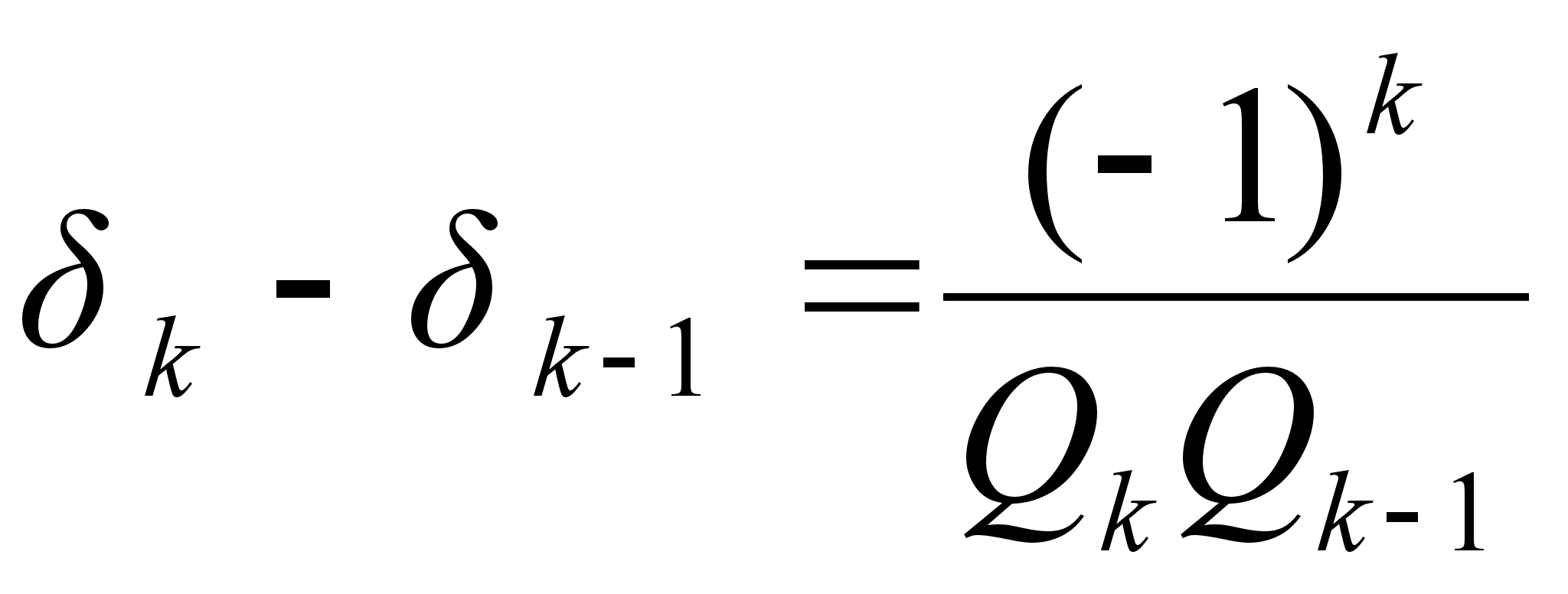 (1) и
(1) и
![]() (2),
(2),
которые справедливы для любой бесконечной непрерывной дроби.
Формула (1) показывает, что любая подходящая дробь четного порядка больше двух соседних подходящих дробей, у которых порядок на единицу меньше или больше, чем у нее, то есть
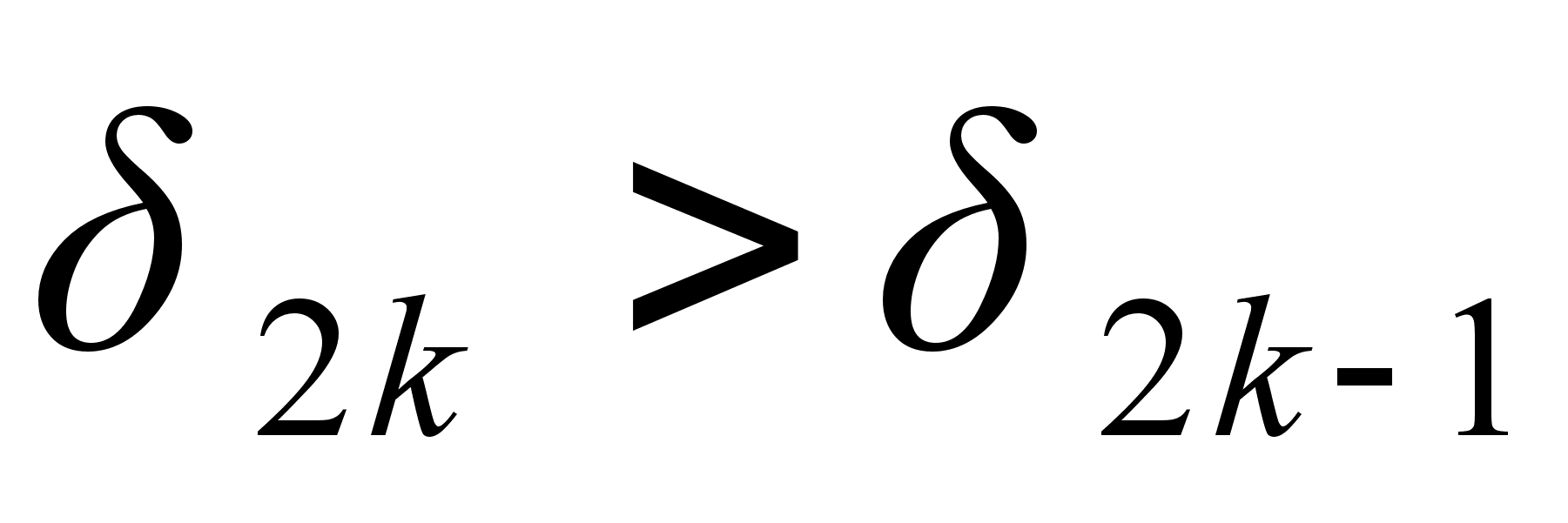 и
и
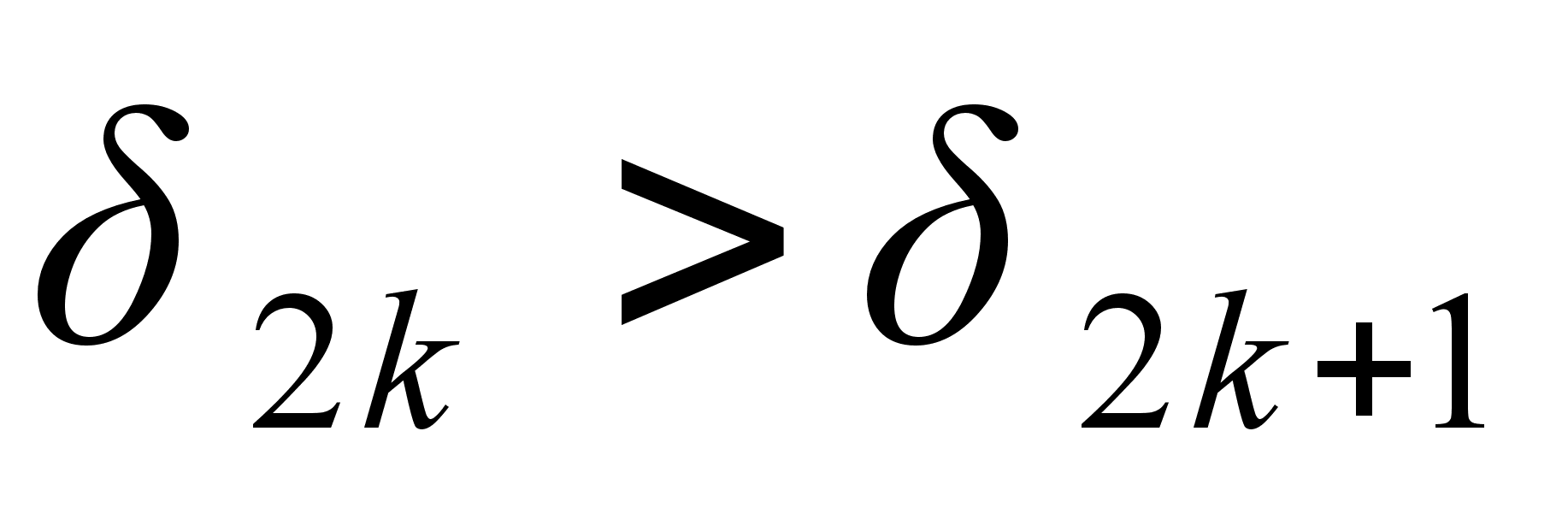 .
Согласно этому
.
Согласно этому
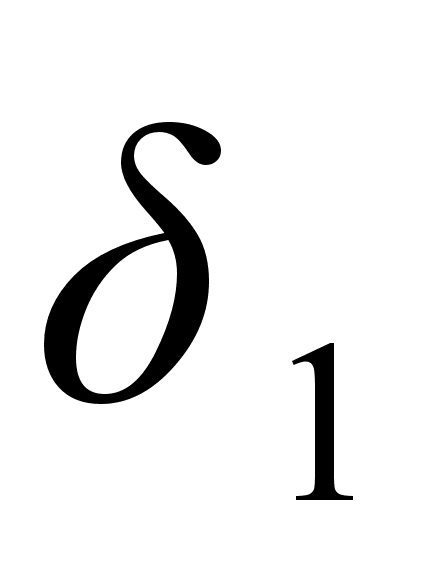 и
и
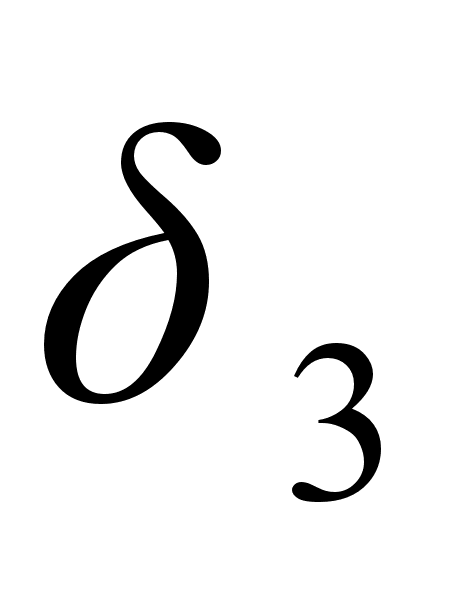 расположены
слева от
расположены
слева от
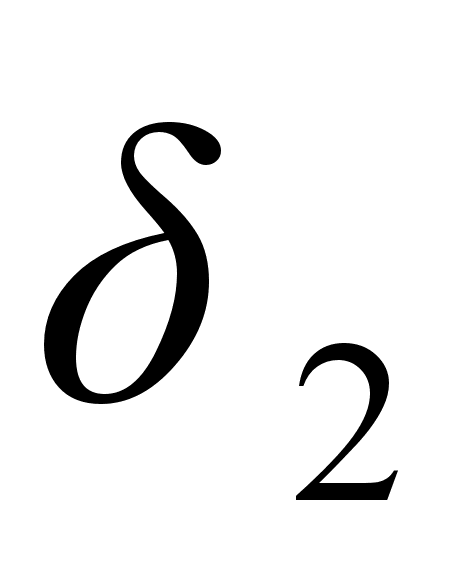 ,
,
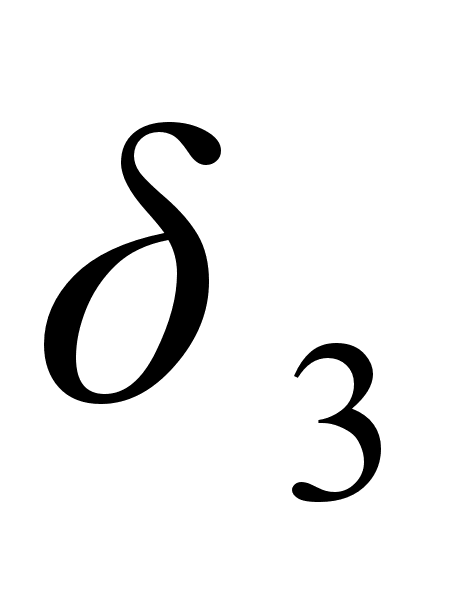 и
и
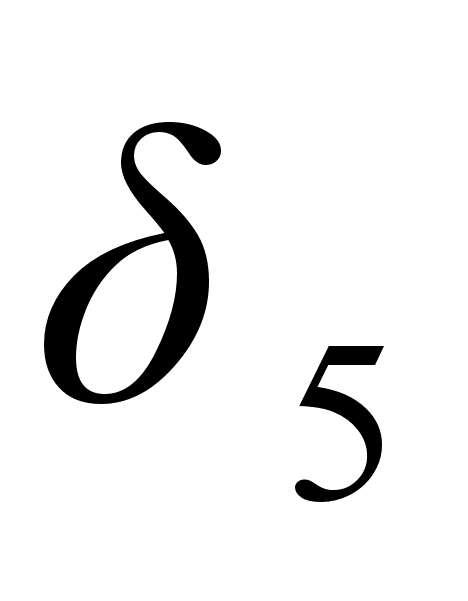 – слева от
– слева от
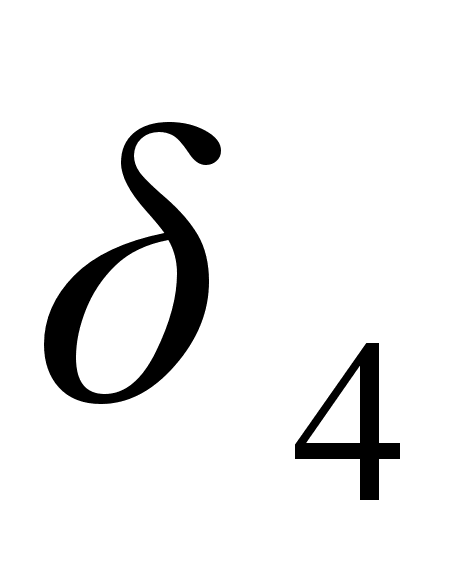 и так далее.
и так далее.Формула (2) показывает, что расстояние между соседними подходящими дробями при увеличении k убывает. Действительно, так как
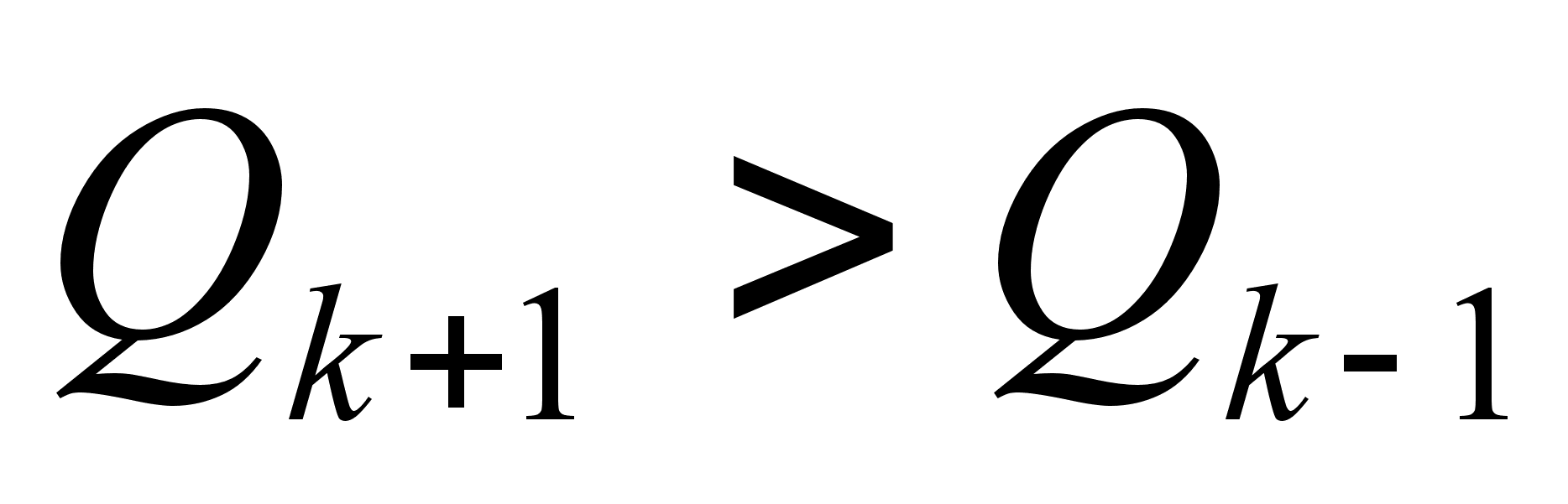 ,
то
,
то
![]()
Согласно этому свойству
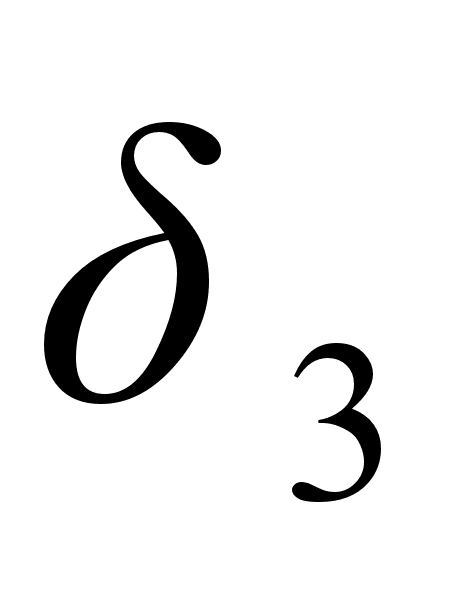 ближе к
ближе к
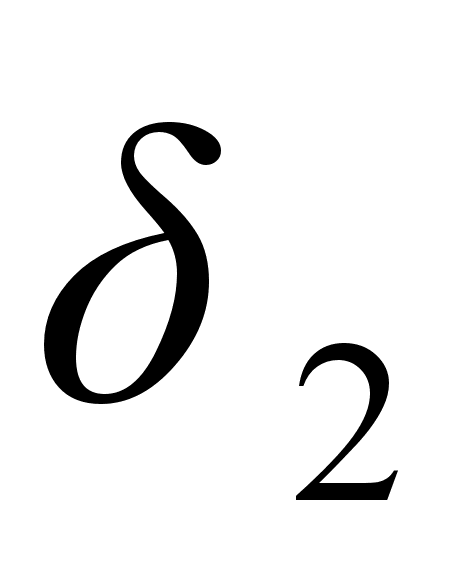 ,
чем
,
чем
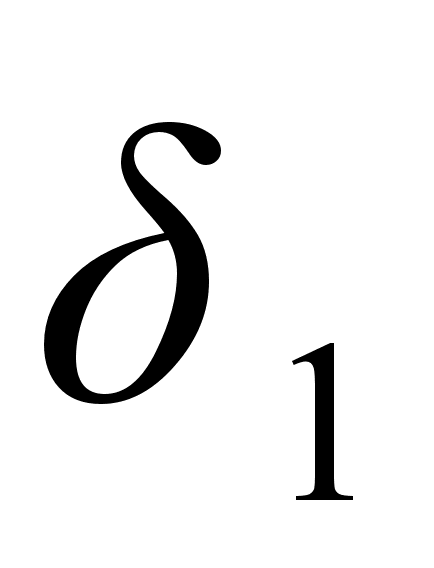 ,
а так как
,
а так как
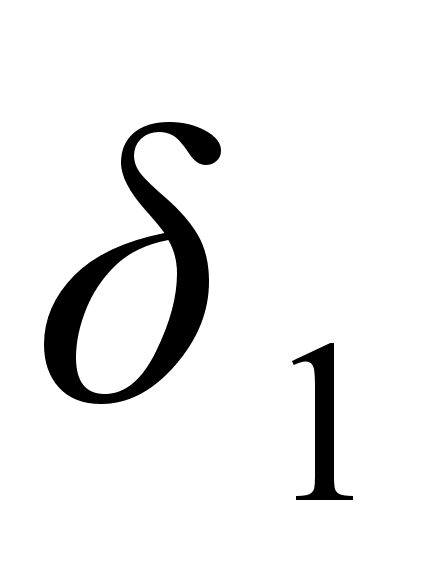 и
и
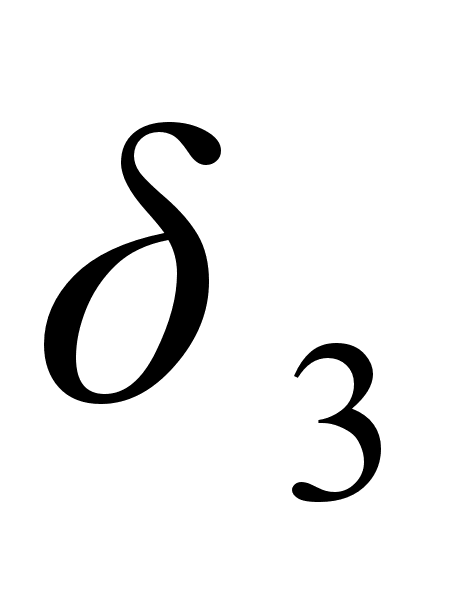 находятся
слева от
находятся
слева от
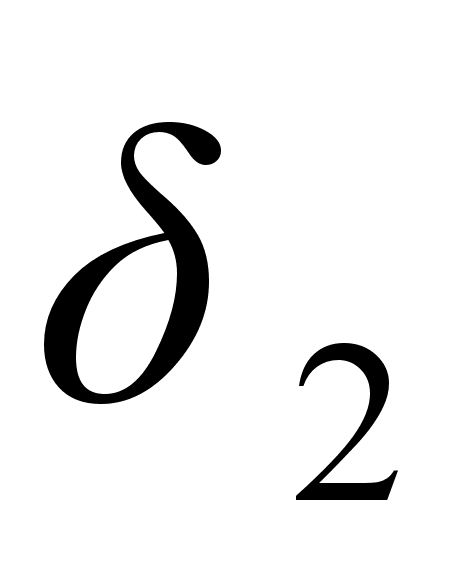 ,
то
,
то
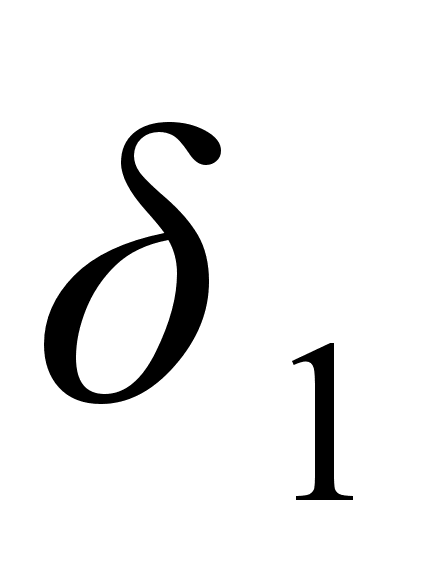
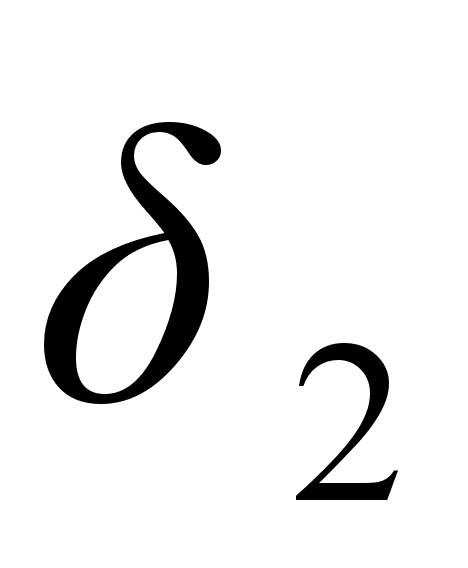 .
.
————![]() ———
———![]() ———
———![]() ———
———![]() ————
————
![]()
![]()
![]()
![]()
Из
этого следует,
что подходящая
дробь
![]() ,
которая, как
и
,
которая, как
и
![]() ,
расположена
справа от
,
расположена
справа от
![]() ,
ближе к
,
ближе к
![]() ,
чем к
,
чем к
![]() ,
то есть
,
то есть
![]()
![]() .
.
Подходящие дроби дальнейших порядков располагаются таким же образом.
Итак,
подходящие
дроби нечетного
порядка увеличиваются
с ростом порядка,
а подходящие
дроби четного
порядка убывают
с ростом порядка;
при этом все
подходящие
дроби нечетного
порядка меньше
всех подходящих
дробей четного
порядка, то
есть
![]()
![]()
![]()
![]()
![]()
![]() при любых
k
и
при любых
k
и
![]() .
.
Так как
![]() ,
то пары подходящих
дробей
,
то пары подходящих
дробей
![]() ,
,
![]() ,
… образуют
стягивающуюся
последовательность
отрезков, которая
должна иметь
единственную
общую точку,
являющуюся
общим пределом
последовательностей
,
… образуют
стягивающуюся
последовательность
отрезков, которая
должна иметь
единственную
общую точку,
являющуюся
общим пределом
последовательностей
![]() ,
,
![]() ,
… и
,
… и
![]() ,
,
![]() ,
…. Обозначим
этот предел
за
,
…. Обозначим
этот предел
за
![]() ,
имеем
,
имеем
![]() ,
причем, очевидно,
,
причем, очевидно,
![]() для
любого
k,
то есть
для
любого
k,
то есть
![]() находится между
любыми двумя
соседними
подходящими
дробями.
находится между
любыми двумя
соседними
подходящими
дробями.
Следовательно,
подходящие
дроби любой
бесконечной
непрерывной
дроби имеют
некоторый
предел
![]() .
Этот предел
.
Этот предел
![]() принимается
в качестве
значения бесконечной
непрерывной
дроби. Говорят,
что бесконечная
непрерывная
дробь сходится
к
принимается
в качестве
значения бесконечной
непрерывной
дроби. Говорят,
что бесконечная
непрерывная
дробь сходится
к
![]() или представляет
число
или представляет
число
![]() .
Можно записать
.
Можно записать
![]() =
=![]() ,
подразумевая
при этом, что
,
подразумевая
при этом, что
![]() =
=![]() .
.
Единственность представления действительного иррационального числа правильной бесконечной цепной дробью.
Исходя
из результатов,
которые мы
получили выше,
можно утверждать,
что для каждого
действительного
иррационального
![]() существует
представление
в виде бесконечной
непрерывной
дроби. Таким
представлением
является разложение
существует
представление
в виде бесконечной
непрерывной
дроби. Таким
представлением
является разложение
![]() в бесконечную
непрерывную
дробь, так как
предел подходящих
дробей последней
равен как раз
в бесконечную
непрерывную
дробь, так как
предел подходящих
дробей последней
равен как раз
![]() .
.
Возникает
вопрос, сколько
представлений
действительного
иррационального
![]() в виде бесконечных
непрерывных
дробей существует
вообще? Покажем,
что только
одно.
в виде бесконечных
непрерывных
дробей существует
вообще? Покажем,
что только
одно.
Другими
словами: представление
действительного
иррационального
![]() в виде бесконечной
непрерывной
дроби всегда
является разложением
в виде бесконечной
непрерывной
дроби всегда
является разложением
![]() с помощью выделения
целой части.
Докажем это
важное утверждение.
с помощью выделения
целой части.
Докажем это
важное утверждение.
Пусть
действительное
иррациональное
![]() представлено
бесконечной
непрерывной
дробью
представлено
бесконечной
непрерывной
дробью
![]() ,
то есть
,
то есть
![]() =
=![]() .
Назовем бесконечную
непрерывную
дробь
.
Назовем бесконечную
непрерывную
дробь
![]() остатком
данной дроби
порядка k.
Так как любая
бесконечная
непрерывная
дробь представляет
некоторое
действительное
число, то это
утверждение
относится также
и к остатку
остатком
данной дроби
порядка k.
Так как любая
бесконечная
непрерывная
дробь представляет
некоторое
действительное
число, то это
утверждение
относится также
и к остатку
![]() .
Обозначим его
через
.
Обозначим его
через
![]() ,
,
![]() =
=![]() ,
то есть
,
то есть
![]() =
=![]() .
Аналогично
.
Аналогично
![]() =
=![]() ,
то есть
,
то есть
![]() =
=![]() .
.
Из
соотношения
![]() получаем
получаем
![]() ,
то есть
,
то есть
![]() =
=![]() (1).
(1).
Так
как при
![]()
![]() ,
то все
,
то все
![]() >1,
а
>1,
а
![]()
![]() ,
то есть
,
то есть
![]() (2). Но
так как
(2). Но
так как
![]() ,
то
,
то
![]() и, ввиду равенства
(1)
и, ввиду равенства
(1)
![]() равно остаточному
числу второго
порядка для
равно остаточному
числу второго
порядка для
![]() ,
то есть
,
то есть
![]() .
Тогда далее
.
Тогда далее
![]() ,
а
,
а
![]() и так далее.
Вообще из
и так далее.
Вообще из
![]() следует
следует
![]() ,
а
,
а
![]() .
.
Элементы
данной бесконечной
непрерывной
дроби получаются
из его значения
![]() последовательным
выделением
целой части,
что и требовалось
доказать.
последовательным
выделением
целой части,
что и требовалось
доказать.
Вместе
с тем мы установили,
что остаток
бесконечной
непрерывной
дроби
![]() =
=![]() порядка
k+1
порядка
k+1
![]() совпадает с
ее остаточным
числом порядка
k+1
совпадает с
ее остаточным
числом порядка
k+1
![]() .
.
Исследования
этого параграфа
приводят нас
к следующему
основному
результату:
каждое иррациональное
действительное
число
![]() единственным
образом представляется
бесконечной
цепной дробью
вида
единственным
образом представляется
бесконечной
цепной дробью
вида
![]() и, наоборот,
каждой бесконечной
цепной дроби
соответствует
единственное
иррациональное
действительное
число, которое
она представляет.
Поэтому множество
всех действительных
чисел взаимно
однозначно
отображается
на множестве
всех непрерывных
дробей (если
условиться,
что для конечных
непрерывных
дробей берется
последнее
и, наоборот,
каждой бесконечной
цепной дроби
соответствует
единственное
иррациональное
действительное
число, которое
она представляет.
Поэтому множество
всех действительных
чисел взаимно
однозначно
отображается
на множестве
всех непрерывных
дробей (если
условиться,
что для конечных
непрерывных
дробей берется
последнее
![]() ).
При этом рациональным
числам соответствуют
конечные непрерывные
дроби, а иррациональным
– бесконечные
дроби.
).
При этом рациональным
числам соответствуют
конечные непрерывные
дроби, а иррациональным
– бесконечные
дроби.
§2. Приближение действительного числа рациональными дробями с заданным ограничением для знаменателя.
Рациональные числа образуют счетное множество, в то время как множество иррациональных чисел несчетно. В этом смысле можно сказать, что основную массу всех действительных чисел составляют иррациональные числа. Применение иррациональных чисел в практике обычно осуществляется заменой данного иррационального числа некоторым рациональным числом, мало отличающимся в пределах требуемой точности от этого иррационального числа. При этом обычно стараются выбрать рациональное число возможно простым, то есть в виде десятичной дроби с небольшим числом знаков после запятой или в виде обыкновенной дроби со сравнительно небольшим знаменателем.
Для громоздких рациональных чисел, то есть чисел с большими знаменателями, также иногда возникают задачи, связанные с необходимостью отыскания хороших рациональных приближений, понимая под этим отыскание рациональных чисел со сравнительно небольшими знаменателями, мало отличающимися от данных чисел.
Цепные дроби дают очень удобный аппарат для решения задач такого рода. С помощью цепных дробей удается заменять действительные числа рациональными дробями так, что ошибка от такой замены мала по сравнению со знаменателями этих рациональных чисел.
2.1. Оценка погрешности при замене действительного числа его подходящей дробью.
Теорема
1: Для
любых двух
соседних подходящих
дробей
![]() и
и
![]() к действительному
числу
к действительному
числу
![]() имеет место
неравенство
имеет место
неравенство
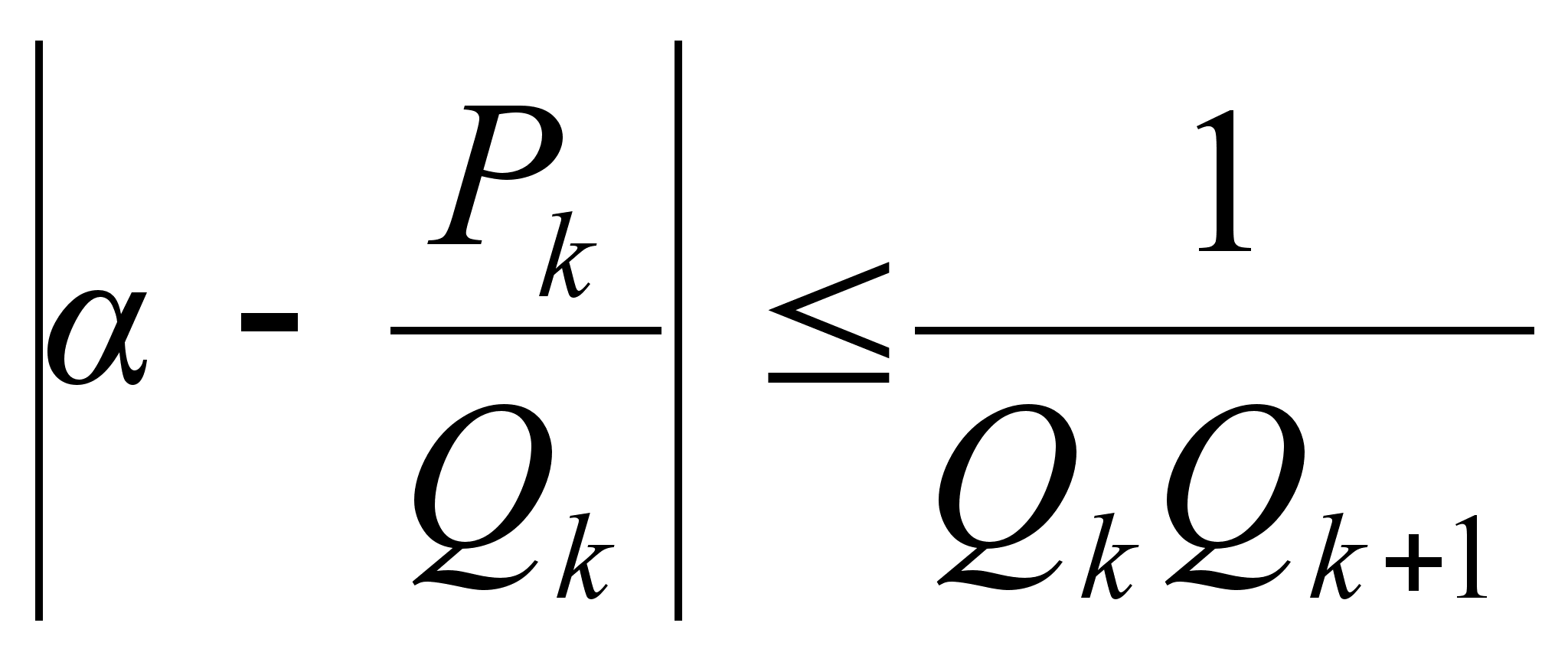 ,
и если
,
и если
![]()
![]() ,
то
,
то
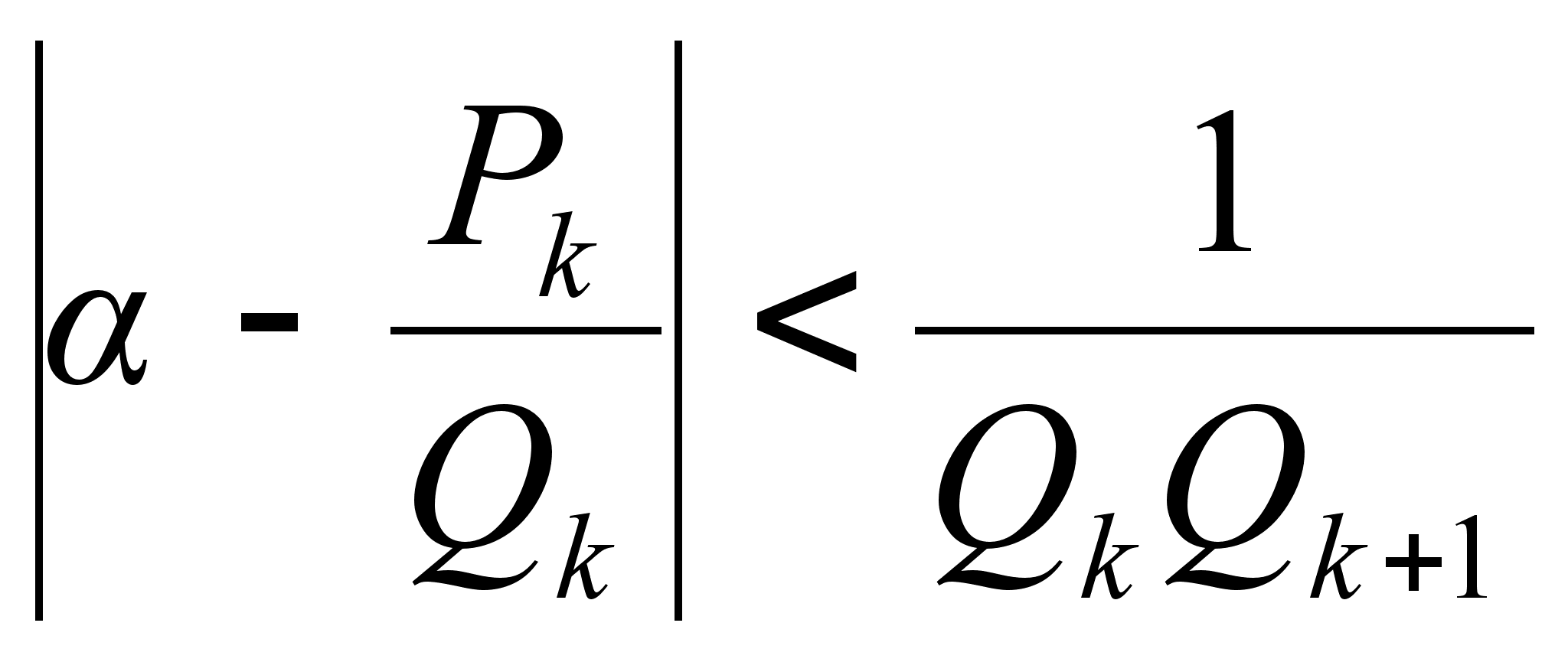 .
.
Доказательство:
Если
![]()
![]() ,
подходящие
дроби
,
подходящие
дроби
![]() и
и
![]() ,
из которых одна
четная, а другая
– нечетная,
лежат по разные
стороны от
,
из которых одна
четная, а другая
– нечетная,
лежат по разные
стороны от
![]() (так как точное
значение непрерывной
дроби находится
между двумя
соседними
подходящими
дробями), и поэтому
расстояние
от
(так как точное
значение непрерывной
дроби находится
между двумя
соседними
подходящими
дробями), и поэтому
расстояние
от
![]() до любой из них
меньше длины
интервала,
образованного
этими двумя
подходящими
дробями, то
есть
до любой из них
меньше длины
интервала,
образованного
этими двумя
подходящими
дробями, то
есть
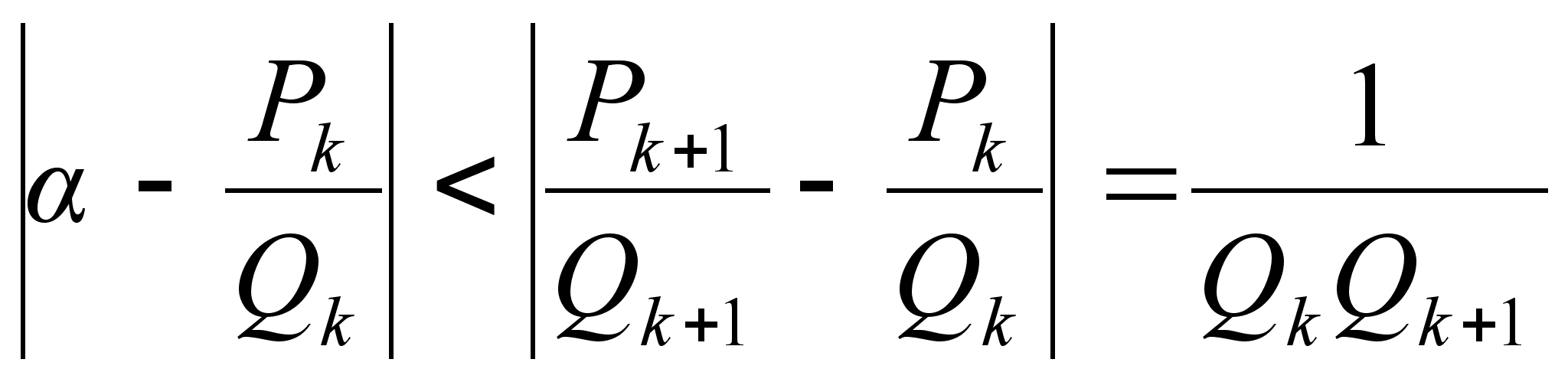 .
.
Если
![]() =
=![]() ,
то
,
то
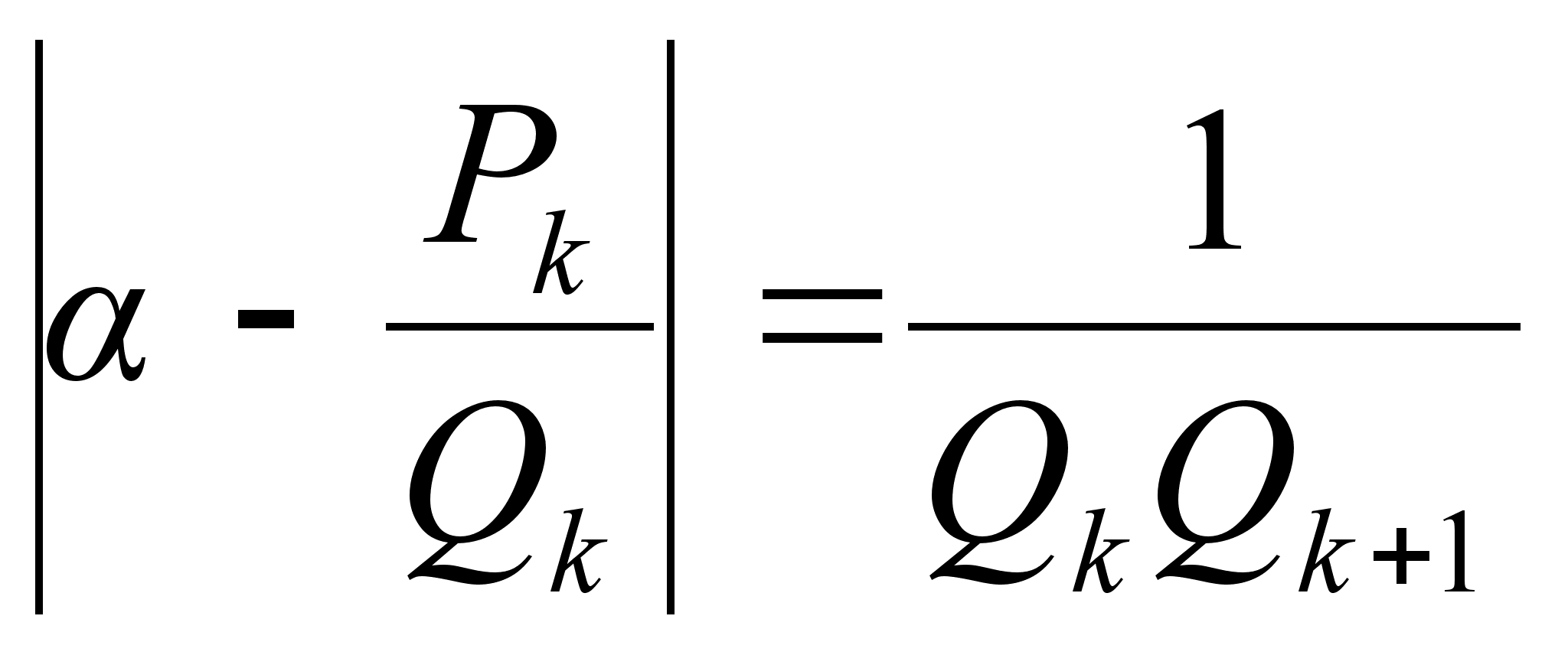 .
.
Теорема
2: Для
любой подходящей
дроби
![]() к действительному
числу
к действительному
числу
![]() справедливо
неравенство:
справедливо
неравенство:
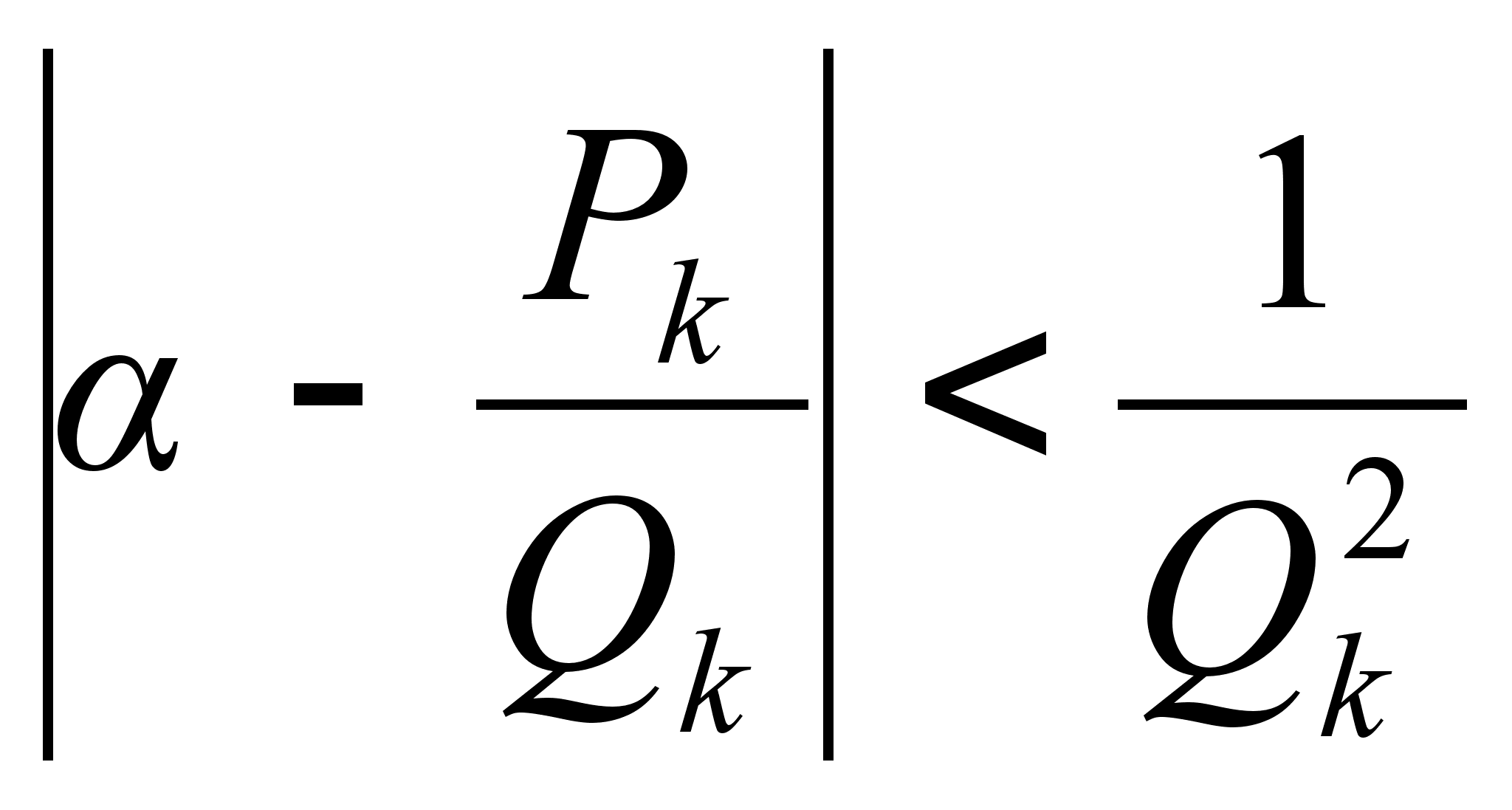
Доказательство:
Если
![]() =
=![]() ,
то получаем,
что левая часть
неравенства
равна нулю, в
то время как
правая часть
всегда больше
нуля. Поэтому
при
,
то получаем,
что левая часть
неравенства
равна нулю, в
то время как
правая часть
всегда больше
нуля. Поэтому
при
![]() =
=![]() неравенство
выполняется.
Пусть
неравенство
выполняется.
Пусть
![]()
![]() ,
то есть существует
подходящая
дробь
,
то есть существует
подходящая
дробь
![]() .
.
При
k>0
![]() и согласно
предыдущей
теореме имеем:
и согласно
предыдущей
теореме имеем:
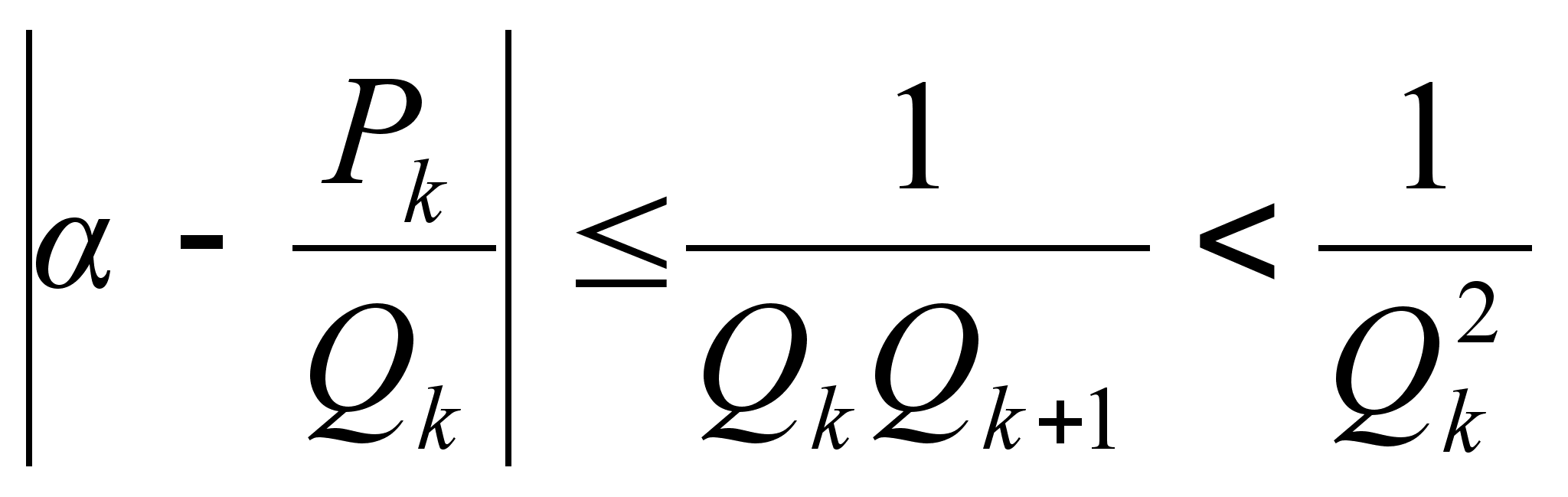 .
.
Отдельно
рассмотрим
случай k=0.
Если
![]() ,
то
,
то
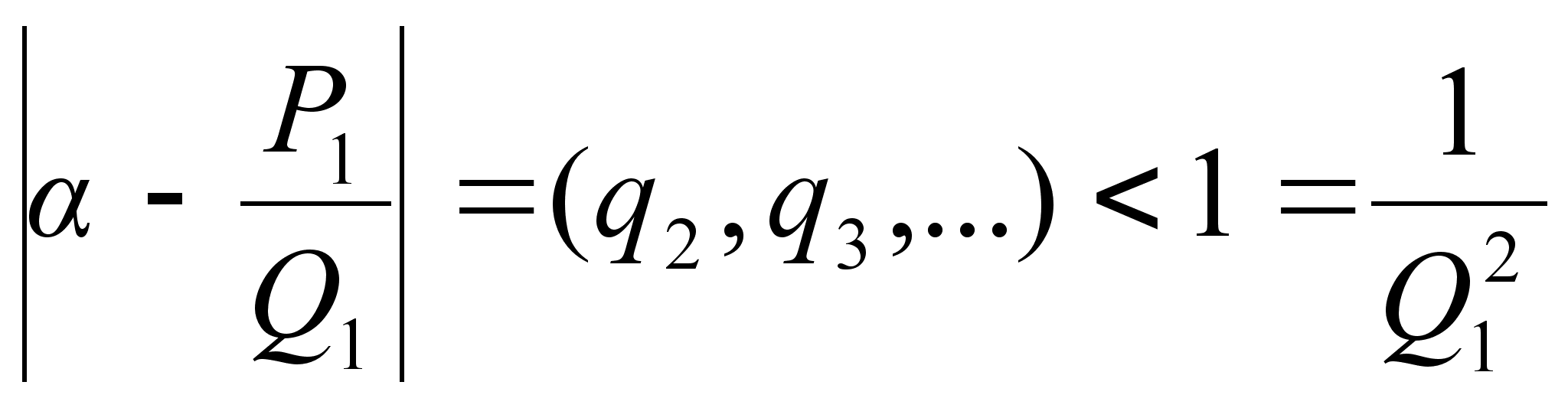 .
.
Теорема
3: Если
![]()
![]() ,
то
,
то
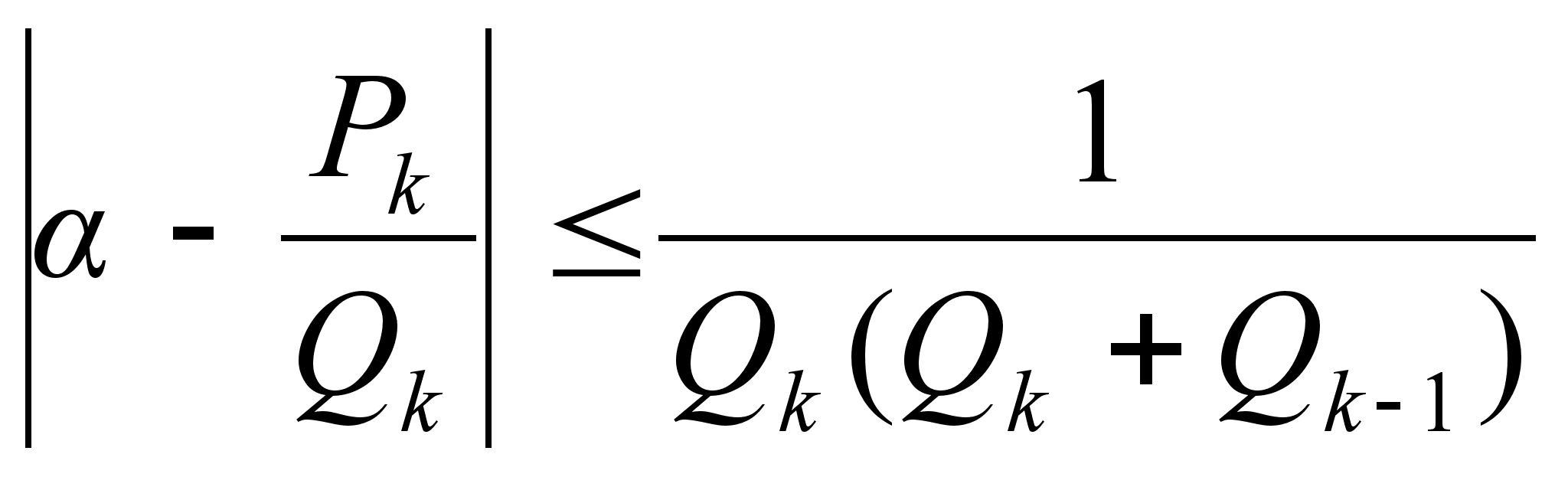 .
.
Из теорем 1-3 получаем следующие оценки погрешности:
![]() ,
,
![]() ,
,
![]()
из которых первая является наиболее точной, а последняя – наиболее грубой.
2.2. Приближение действительного числа подходящими дробями.
Решение поставленной задачи начнем с рассмотрения нескольких примеров.
Пример 1: Рассмотрим задачу, аналогичную той, с которой встретился голландский математик Христиан Гюйгенс (1629-1695) при построении модели солнечной системы с помощью набора зубчатых колес и которая привела его к открытию ряда важных свойств непрерывных дробей.
Пусть
требуется,
чтобы отношение
угловых скоростей
двух зацепляющихся
зубчатых колес
II
и
I было
равно
![]() .
.
Так как
угловые скорости
колес обратно
пропорциональны
числам зубцов,
то отношение
чисел зубцов
колес
I и
II должно
быть равно
![]() .
Если
.
Если
![]() –
несократимая
дробь
–
несократимая
дробь
![]() с большим числителем
и знаменателем,
например,
с большим числителем
и знаменателем,
например,
![]() ,
то для точного
решения задачи
возникает
техническая
трудность
изготовления
колес с большим
количеством
зубцов.
,
то для точного
решения задачи
возникает
техническая
трудность
изготовления
колес с большим
количеством
зубцов.
Задачу можно технически упростить при помощи колес с меньшим количеством зубцов. При этом важно, чтобы отношение этих чисел было, по возможности, ближе к заданному отношению. Хорошего удовлетворения поставленных требований можно добиться, если воспользоваться непрерывными дробями.
Пусть,
например, поставлено
требование
заменить
N
и
n
меньшими числами
![]() и
и
![]() так, чтобы
так, чтобы
![]() и чтобы отношение
и чтобы отношение
![]() было, по возможности,
ближе к
было, по возможности,
ближе к
![]() .
.
Применяя
аппарат цепных
дробей, можем
дать следующее
решение этой
задачи: разлагаем
![]() в непрерывную
дробь и берем
ее подходящую
дробь с наибольшим
знаменателем,
не превышающим
100.
в непрерывную
дробь и берем
ее подходящую
дробь с наибольшим
знаменателем,
не превышающим
100.
Получаем,
![]() =(1,
2, 3, 7, 8, 2)
=(1,
2, 3, 7, 8, 2)
Составляя схему, находим:
|
1 |
2 |
3 |
7 |
8 |
2 |
|
|
|
1 |
3 |
10 |
73 |
594 |
1261 |
|
|
1 |
2 |
7 |
51 |
415 |
881 |
Поставленному
условию удовлетворяет
подходящая
дробь
![]() .
При этом допущенная
погрешность
.
При этом допущенная
погрешность
![]()
![]() ,
то есть весьма
незначительна.
,
то есть весьма
незначительна.
Ответ:
![]() .
.
Для
иррационального
![]() по существу
возможно лишь
приближенное
решение задачи.
по существу
возможно лишь
приближенное
решение задачи.
Пример
2: Как мы уже
определили
ранее
![]() .
Вычислим
.
Вычислим
![]() с точностью
до 0,001.
с точностью
до 0,001.
Для решения
придется найти
такую подходящую
дробь
![]() разложения
разложения
![]() ,
чтобы
,
чтобы
![]() .
.
Сделаем это, используя схему:
|
3 |
3 |
6 |
3 |
|
|
|
3 |
10 |
63 |
199 |
|
|
1 |
3 |
19 |
60 |
Очевидно,
нам достаточно
взять
![]() ,
так как 19·60>1000.
Это значение
будет равно
,
так как 19·60>1000.
Это значение
будет равно
![]() с точностью
до 0,001,
причем с недостатком,
так как
с точностью
до 0,001,
причем с недостатком,
так как
![]() –
подходящая
дробь нечетного
порядка. Мы
можем представить
–
подходящая
дробь нечетного
порядка. Мы
можем представить
![]() в виде десятичной
дроби, причем
имеем право
взять 3 знака
после запятой,
так как
в виде десятичной
дроби, причем
имеем право
взять 3 знака
после запятой,
так как
![]() является приближенным
значением для
является приближенным
значением для
![]() с точностью
до
0,001. Получаем
с точностью
до
0,001. Получаем
![]() (мы округляем
по избытку, так
как
(мы округляем
по избытку, так
как
![]() является приближенным
значением с
недостатком,
однако, не можем
теперь сказать,
будет ли
3,316
приближенным
значением
является приближенным
значением с
недостатком,
однако, не можем
теперь сказать,
будет ли
3,316
приближенным
значением
![]() с недостатком
или избытком).
с недостатком
или избытком).
Решенные задачи в более общем виде формулируются так:
Найти рациональное приближение к действительному
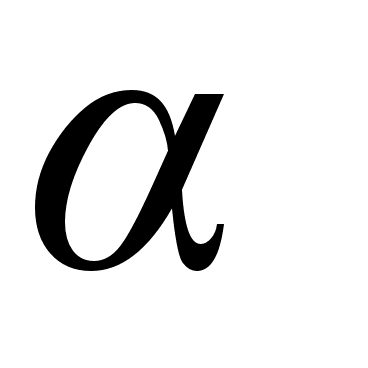 со знаменателем
со знаменателем
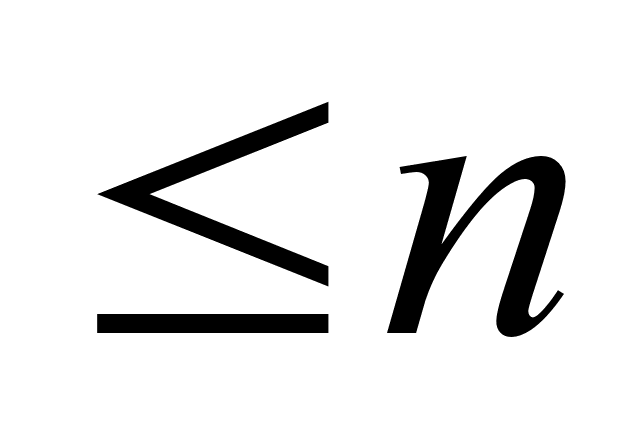 в виде наиболее
близкой к
в виде наиболее
близкой к
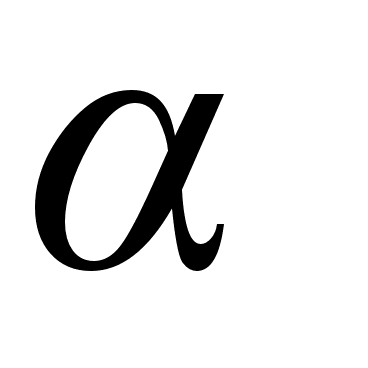 подходящей
дроби. Для этого
надо взять
подходящую
дробь для
подходящей
дроби. Для этого
надо взять
подходящую
дробь для
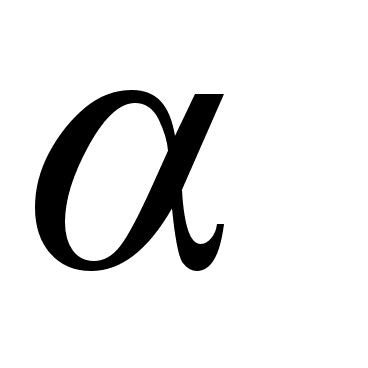 с наибольшим
знаменателем,
не превышающим
n.
с наибольшим
знаменателем,
не превышающим
n.Найти рациональное приближение к действительному числу
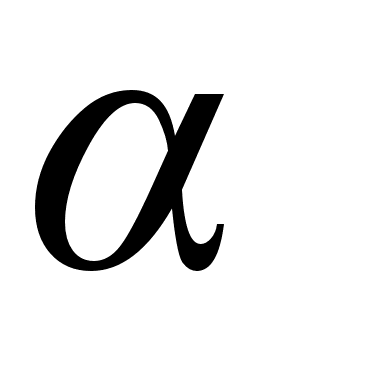 с возможно
меньшим знаменателем
так, чтобы
погрешность
не превосходила
с возможно
меньшим знаменателем
так, чтобы
погрешность
не превосходила
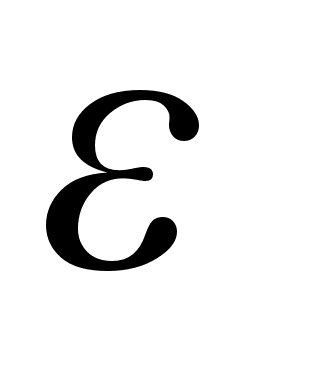 (то есть с точностью
до
(то есть с точностью
до
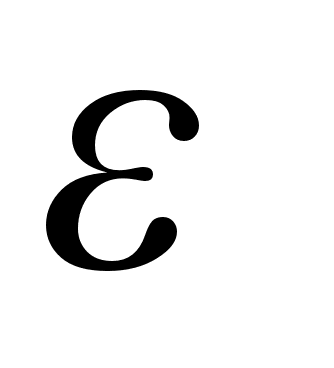 ).
Для этого, пользуясь
аппаратом
цепных дробей,
находим подходящую
дробь
).
Для этого, пользуясь
аппаратом
цепных дробей,
находим подходящую
дробь
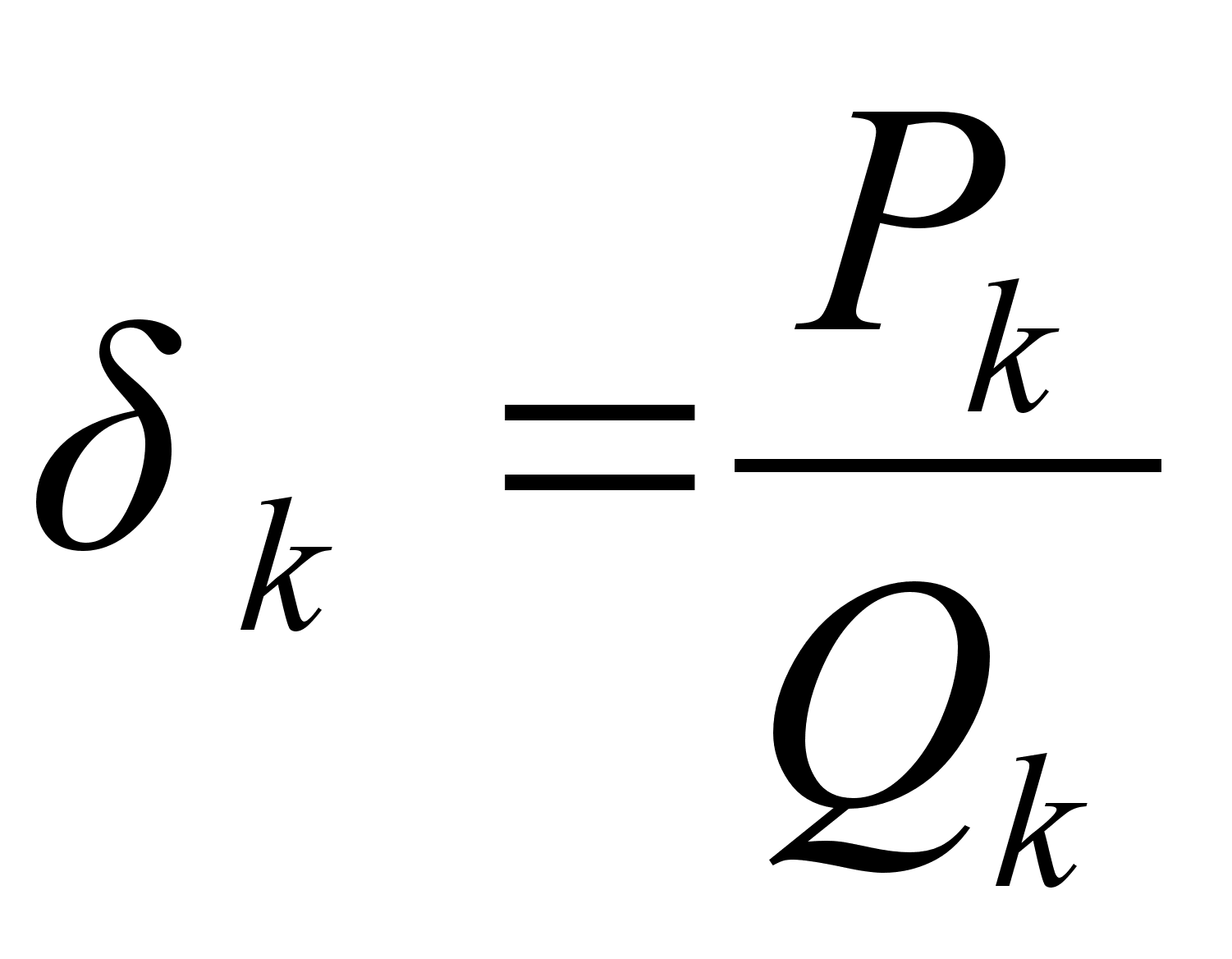 с наименьшим
знаменателем
с наименьшим
знаменателем
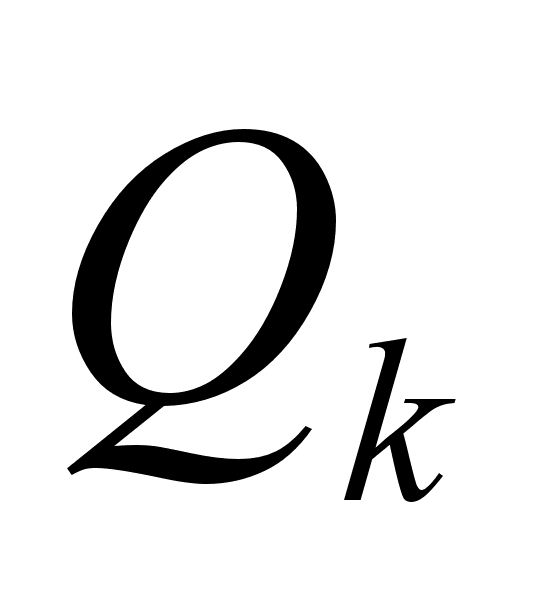 так, чтобы
так, чтобы
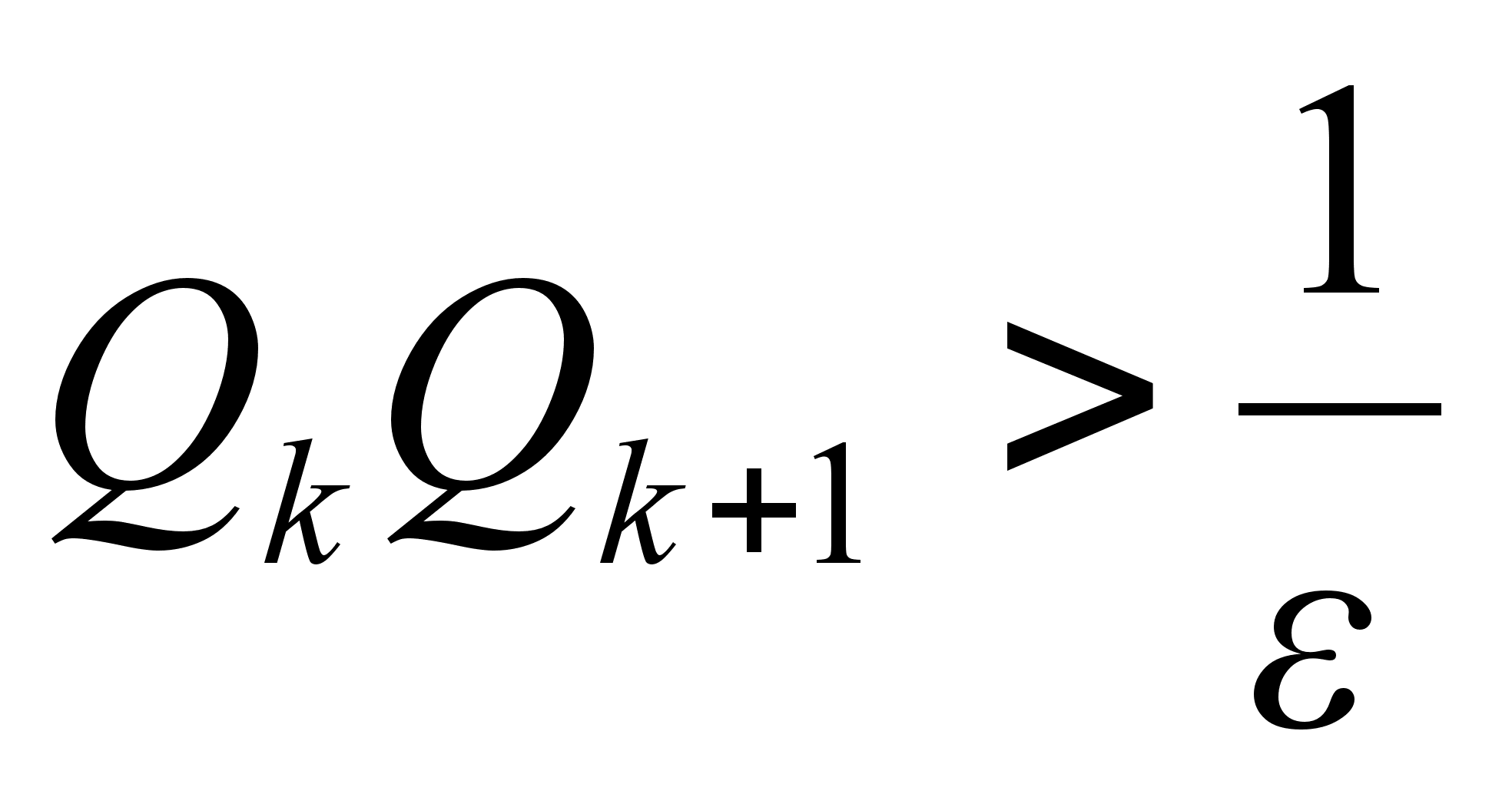 .
.
2.3. Теорема Дирихле.
Выше
мы нашли оценку
погрешности,
возникающей
при замене
любого действительного
числа
![]() рациональными
дробями определенного
типа, а именно:
подходящими
дробями.
рациональными
дробями определенного
типа, а именно:
подходящими
дробями.
А сейчас рассмотрим некоторые сравнительно простые результаты, показывающие как обстоит дело с приближением действительных чисел рациональными числами, не предрешая заранее, что эти рациональные числа будут подходящими дробями.
Пусть
![]() –
произвольное
действительное
число. Из теории
десятичных
дробей следует
существование
рационального
числа
–
произвольное
действительное
число. Из теории
десятичных
дробей следует
существование
рационального
числа
![]() такого, что
такого, что
![]() .
поставим вопрос
о возможности
таких приближений
.
поставим вопрос
о возможности
таких приближений
![]() рациональными
числами
рациональными
числами
![]() ,
при которых
точность приближения
будет оценена
не величиной
,
при которых
точность приближения
будет оценена
не величиной
![]() ,
а величиной,
в
,
а величиной,
в
![]() раз
меньшей, то
есть вопрос
о нахождении
рациональных
чисел
раз
меньшей, то
есть вопрос
о нахождении
рациональных
чисел
![]() таких, что
таких, что
![]() ,
где
,
где
![]() – любое
заранее положительное
число.
– любое
заранее положительное
число.
Например,
можно поставить
задачу нахождения
такого рационального
приближения
к
![]() ,
чтобы точность
приближения
была в
1000 или
в
1000000 раз
лучшей, чем
величина, обратная
знаменателю.
Это соответствует
выбору
,
чтобы точность
приближения
была в
1000 или
в
1000000 раз
лучшей, чем
величина, обратная
знаменателю.
Это соответствует
выбору
![]() =1000
или
=1000
или
![]() =1000000.
оказывается,
что как бы велико
ни было
=1000000.
оказывается,
что как бы велико
ни было
![]() ,
можно найти
рациональную
дробь
,
можно найти
рациональную
дробь
![]() ,
приближающую
,
приближающую
![]() с точностью
до
с точностью
до
![]() ,
причем и это
является самым
интересным,
дробь
,
причем и это
является самым
интересным,
дробь
![]() мы можем выбрать
так, что
мы можем выбрать
так, что
![]() .
.
Теорема
Дирихле:
Пусть
![]() и
и
![]() –
действительные
числа; существует
несократимая
дробь
–
действительные
числа; существует
несократимая
дробь
![]() ,
для которой
,
для которой
![]() ,
,
![]()
(или:
существует
такая пара
взаимно простых
целых чисел
a
и b,
что
![]() ,
,
![]() ).
).
Доказательство: Теорему легко доказать с помощью аппарата цепных дробей.
Пусть
![]() подходящая
дробь числа
подходящая
дробь числа
![]() ;
выберем наибольший
из знаменателей
;
выберем наибольший
из знаменателей
![]() ,
не превышающий
,
не превышающий
![]() ,
то есть наибольшее
k,
чтобы
,
то есть наибольшее
k,
чтобы
![]()
![]() и положим
и положим
![]() =
=![]() .
Рассмотрим
два случая:
.
Рассмотрим
два случая:
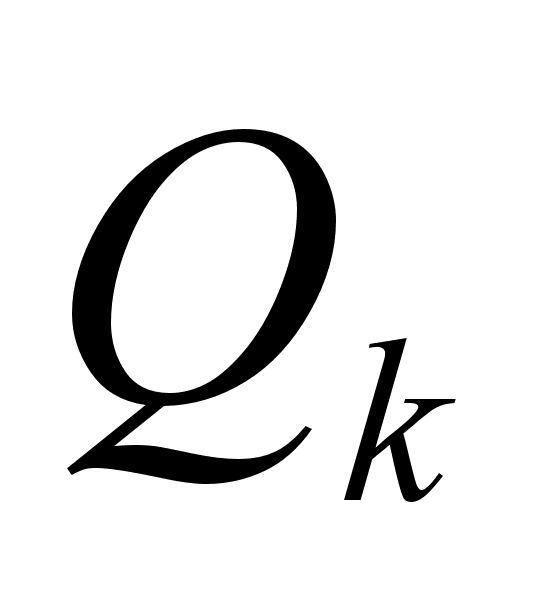 не является
последним
знаменателем,
то есть существует
не является
последним
знаменателем,
то есть существует
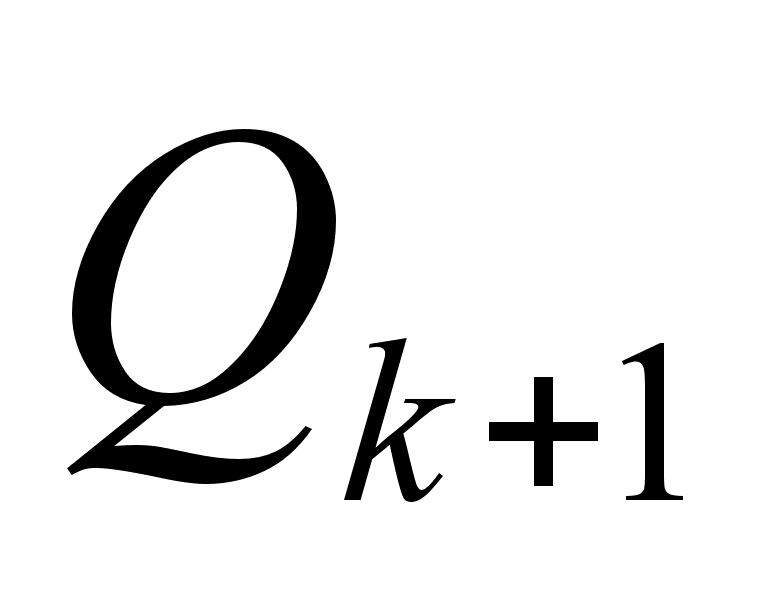 такое, что
такое, что
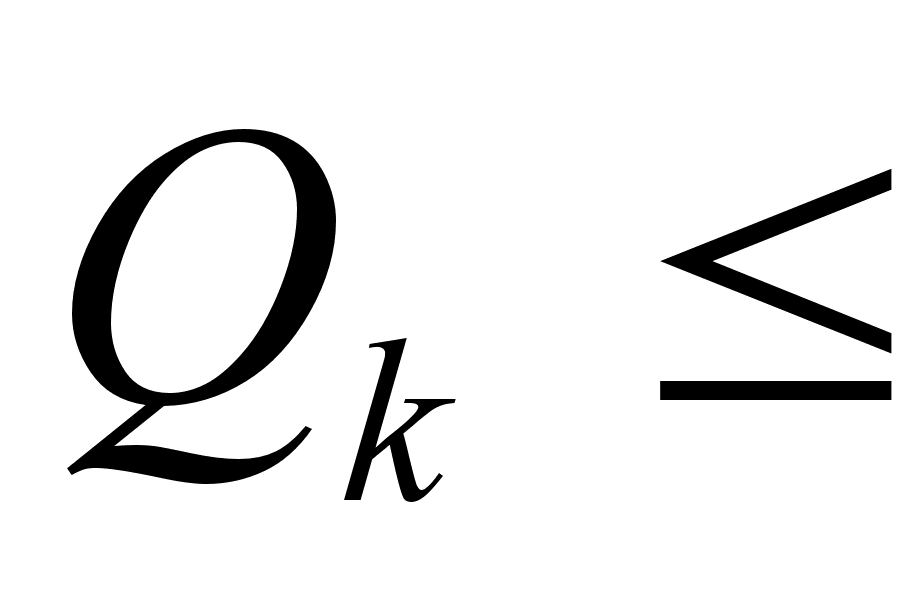

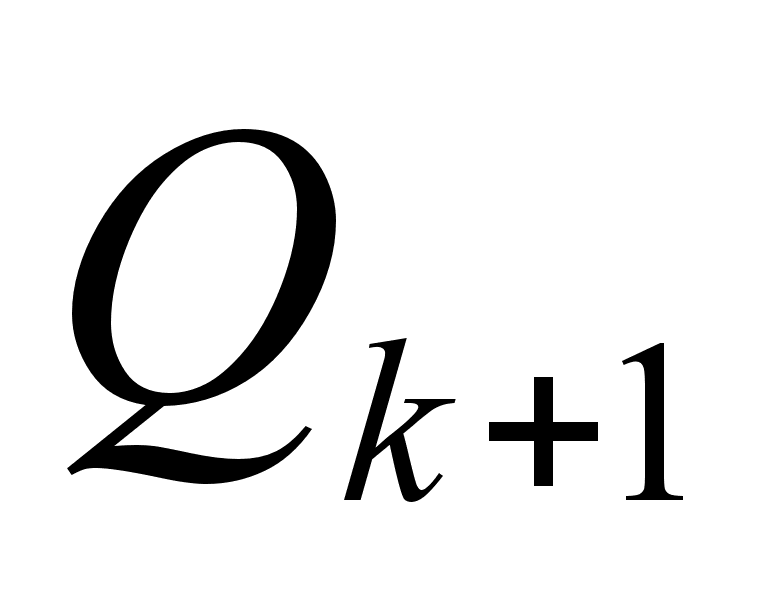 .
Тогда при a=
.
Тогда при a=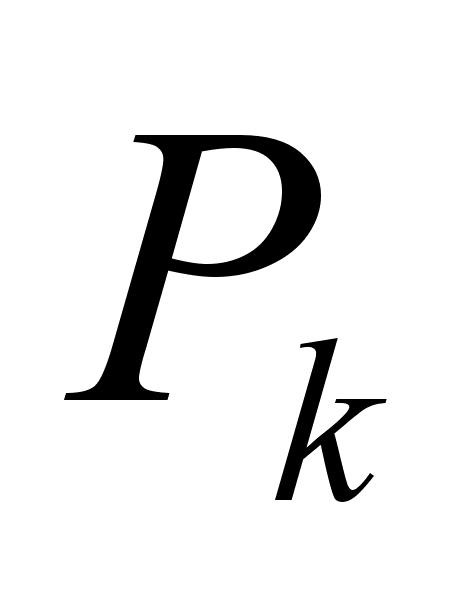 и b=
и b=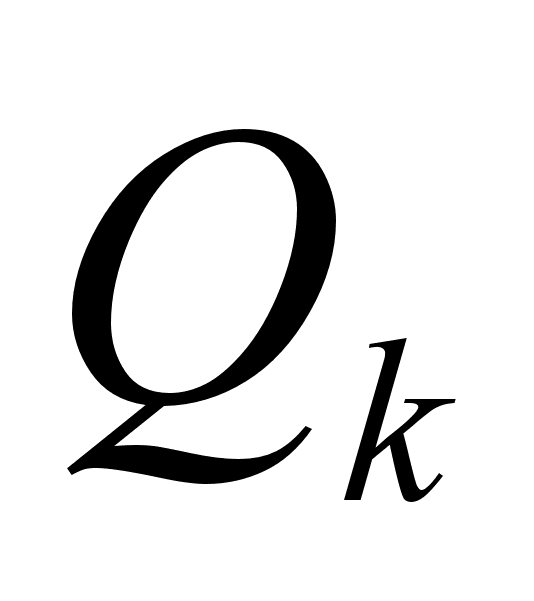 имеем:
имеем:
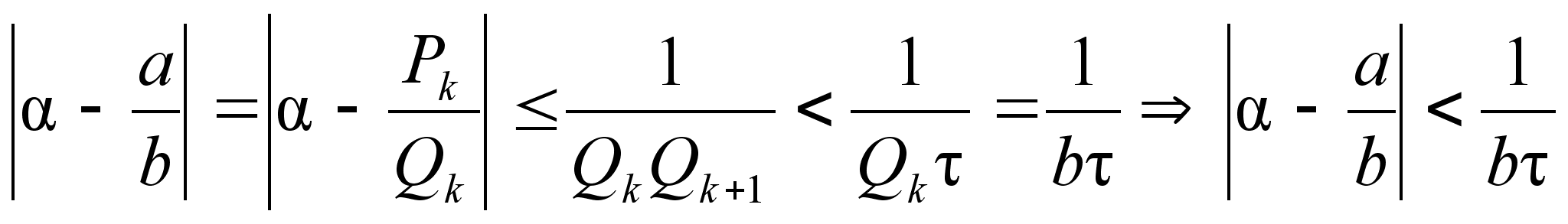
2)
![]() –
знаменатель
последней
подходящей
дроби разложения
–
знаменатель
последней
подходящей
дроби разложения
![]() ,
то есть
,
то есть
![]() =
=![]() .
Тогда при a=
.
Тогда при a=![]() ,
b=
,
b=![]() ,
имеем:
,
имеем:
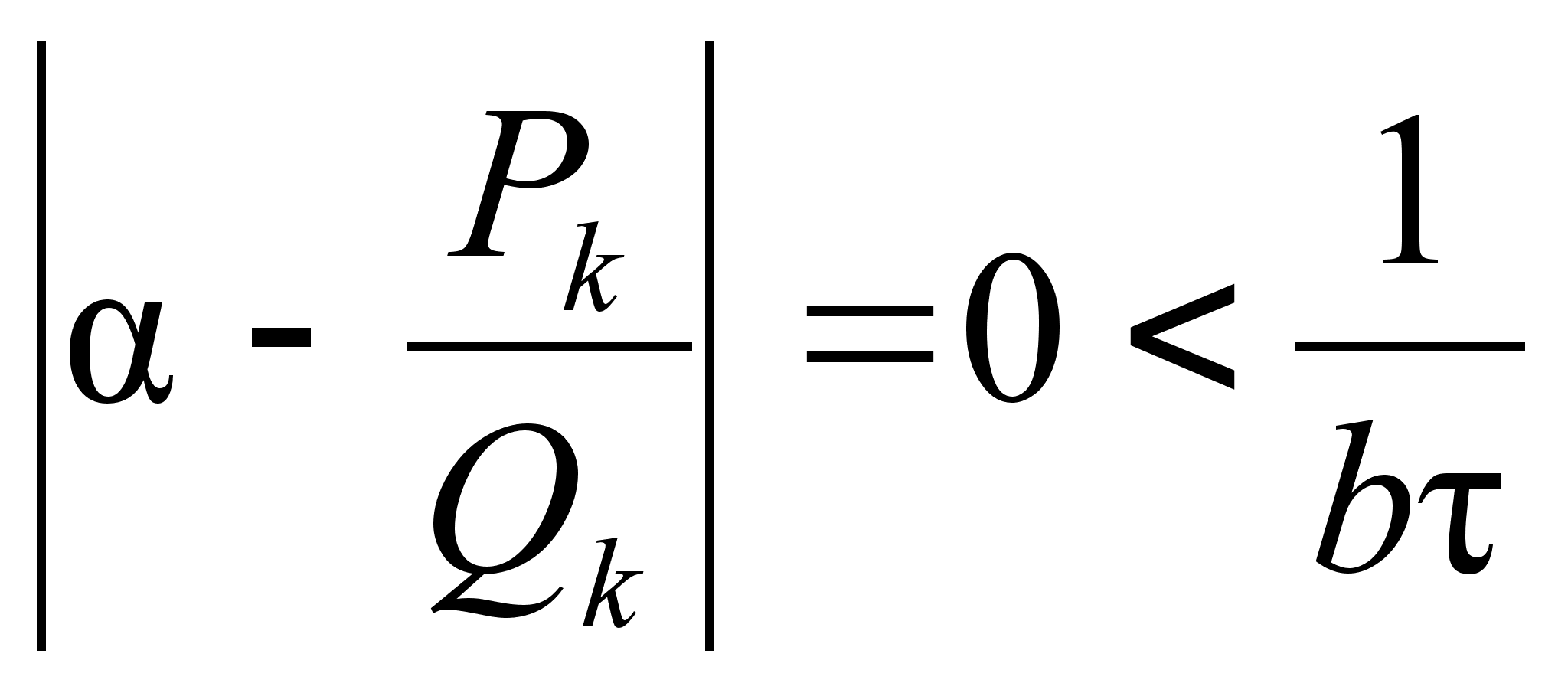 .
.
Теорема доказана.
Сам Дирихле дал другое доказательство, использовав в нем принцип, который носит теперь имя Дирихле: при распределении N объектов между N-1 ящиками хотя бы в одном ящике должно находиться 2 объекта. Приведем это доказательство.
Пусть
![]() ,
рассмотрим
совокупность
t+2
чисел, состоящую
из
1 и
значений дробных
частей
,
рассмотрим
совокупность
t+2
чисел, состоящую
из
1 и
значений дробных
частей
![]() для x=0,
1, …, t
(причем
для x=0,
1, …, t
(причем
![]() =
=![]() -
-![]() ,
,
![]() ).
Очевидно, каждое
из чисел этой
совокупности
принадлежит
точно одному
из
t+1
промежутков
).
Очевидно, каждое
из чисел этой
совокупности
принадлежит
точно одному
из
t+1
промежутков
![]() ,
,
![]() ,
…,
,
…,
![]() ,
из которых
первые
t
являются
полусегментами,
а последний
сегментом.
,
из которых
первые
t
являются
полусегментами,
а последний
сегментом.
————![]() ————
————![]() ————
————![]() ——————————————
——————————————![]() ————
————![]() ——
——
0
![]()
![]()
![]() 1
1
Так
как чисел у нас
t+2,
то (согласно
принципу Дирихле)
обязательно
найдется такой
промежуток,
который содержит
2 числа
из совокупности
![]() и 1.
Разность этих
двух чисел не
превосходит
длину содержащего
их промежутка,
то есть
и 1.
Разность этих
двух чисел не
превосходит
длину содержащего
их промежутка,
то есть
![]() .
.
Если такими числами являются
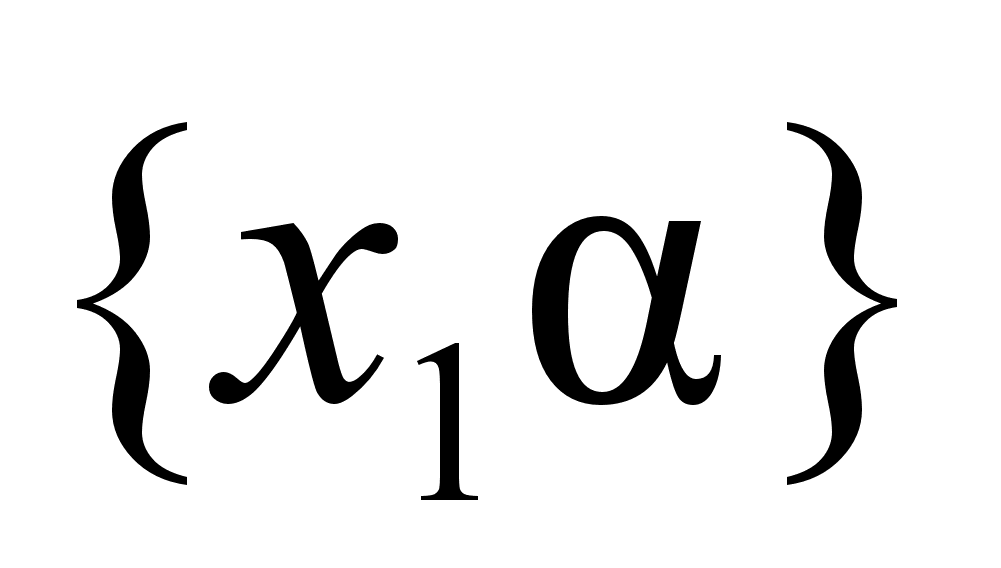 и
и
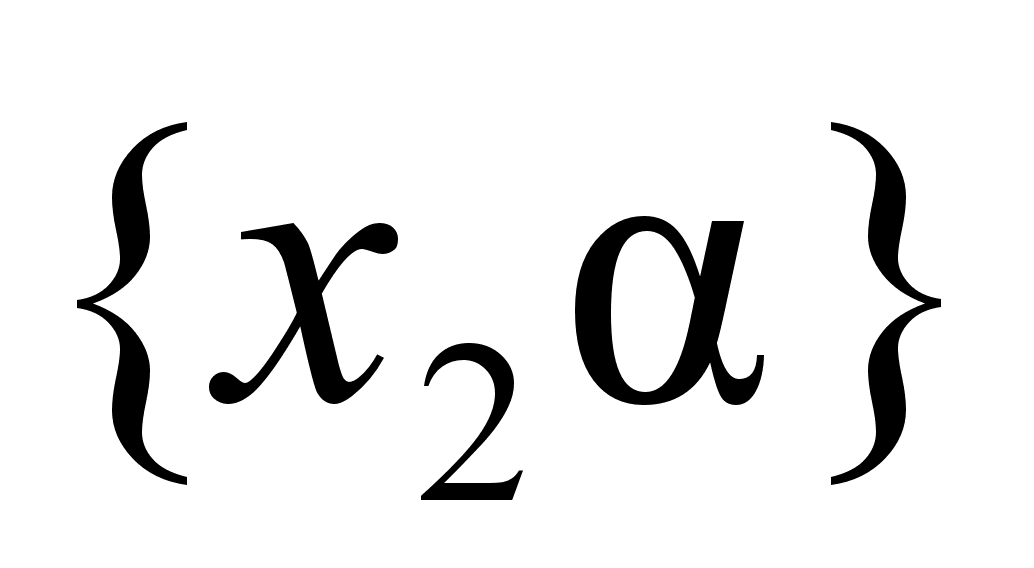 ,
то
,
то
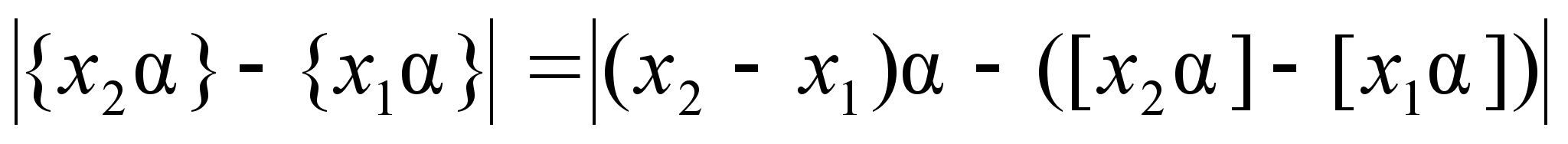 .
Пусть
.
Пусть
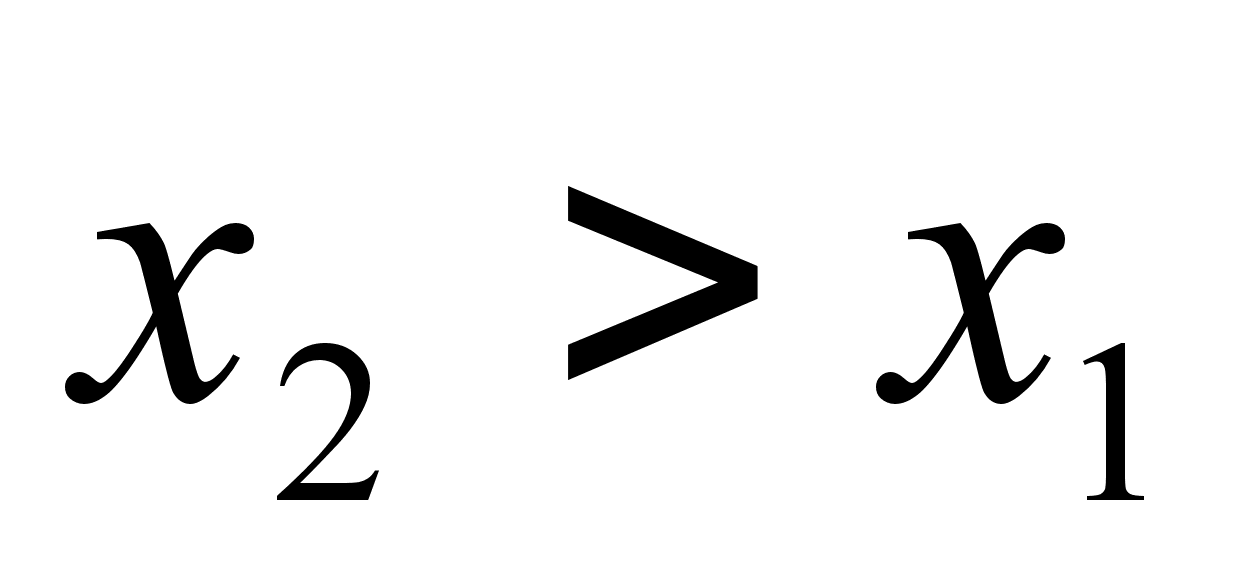 и
и
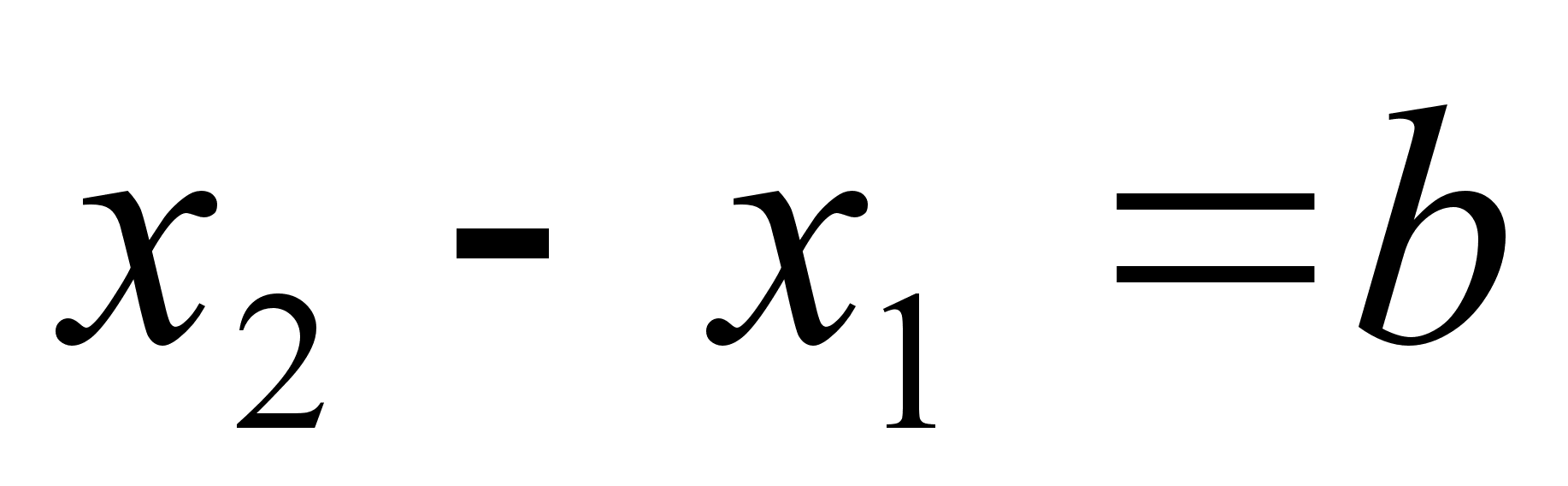 ,
,
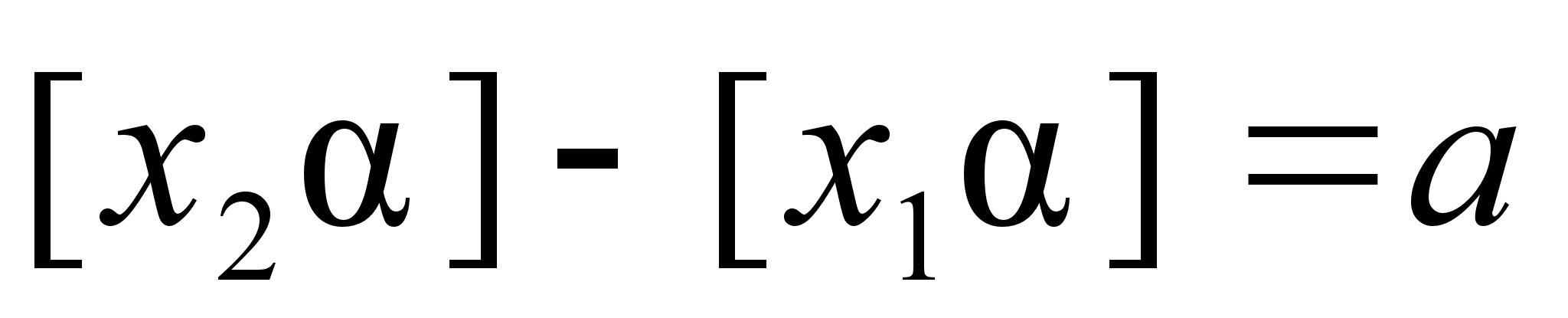 .
Так как
.
Так как
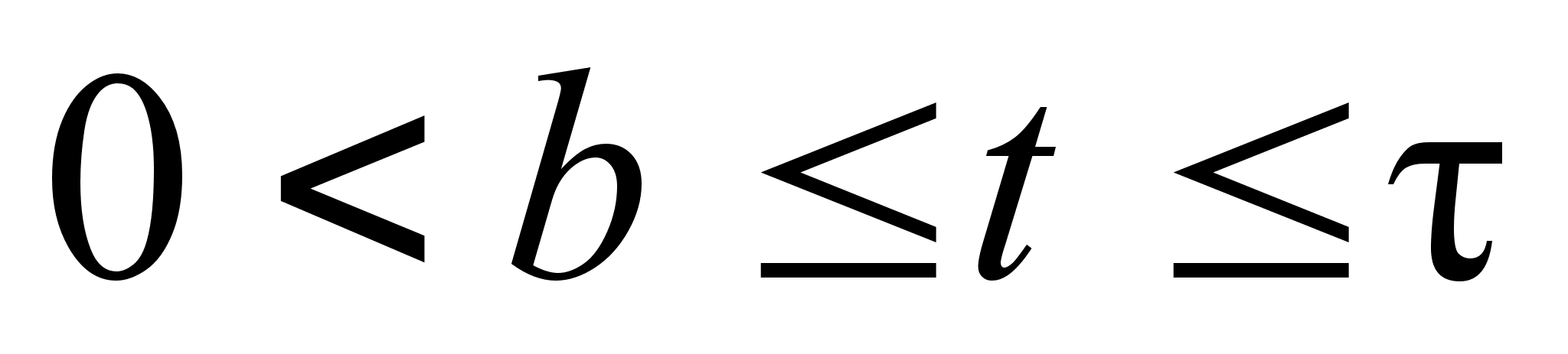 ,
то
,
то
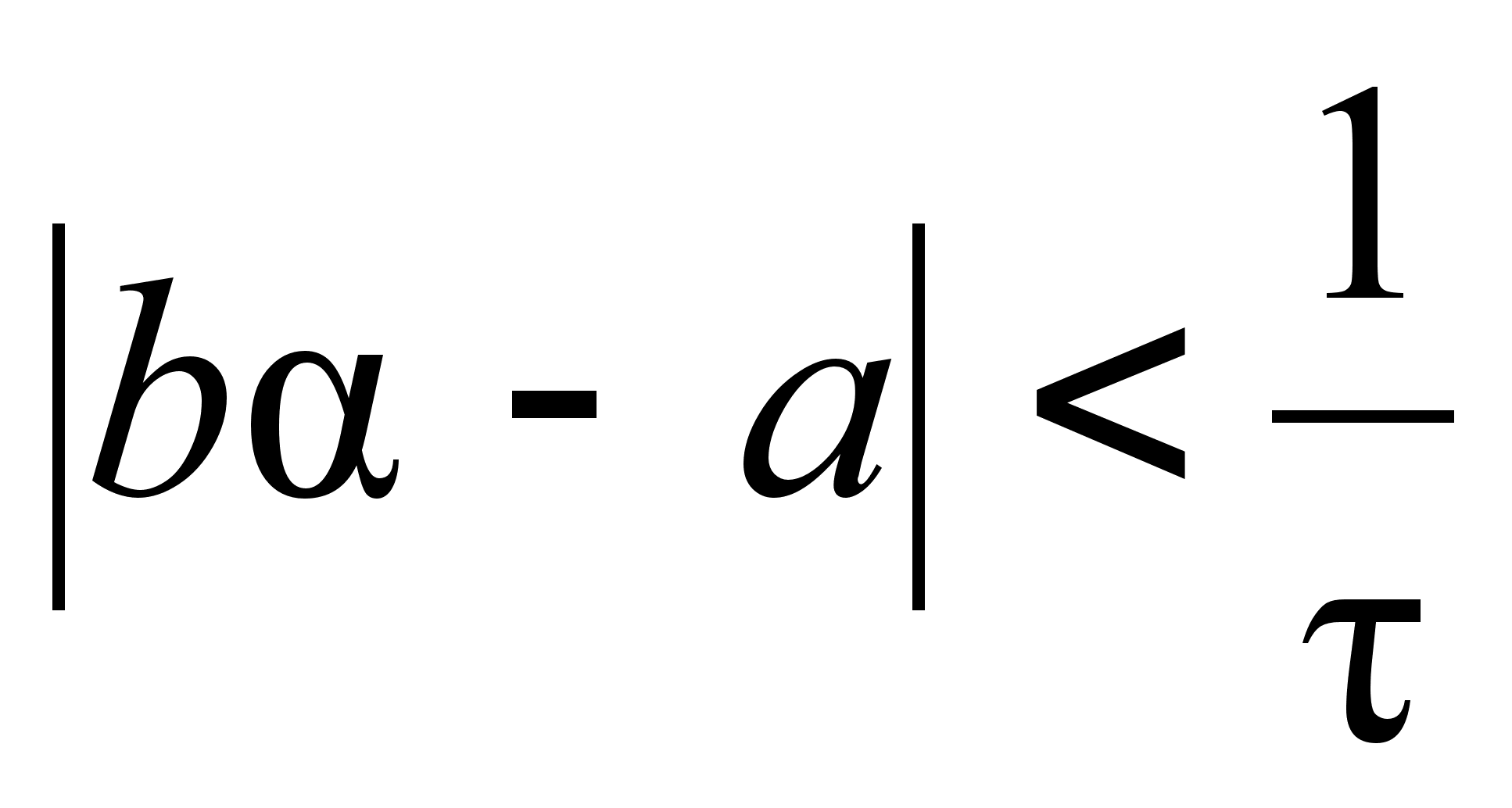 ,
,
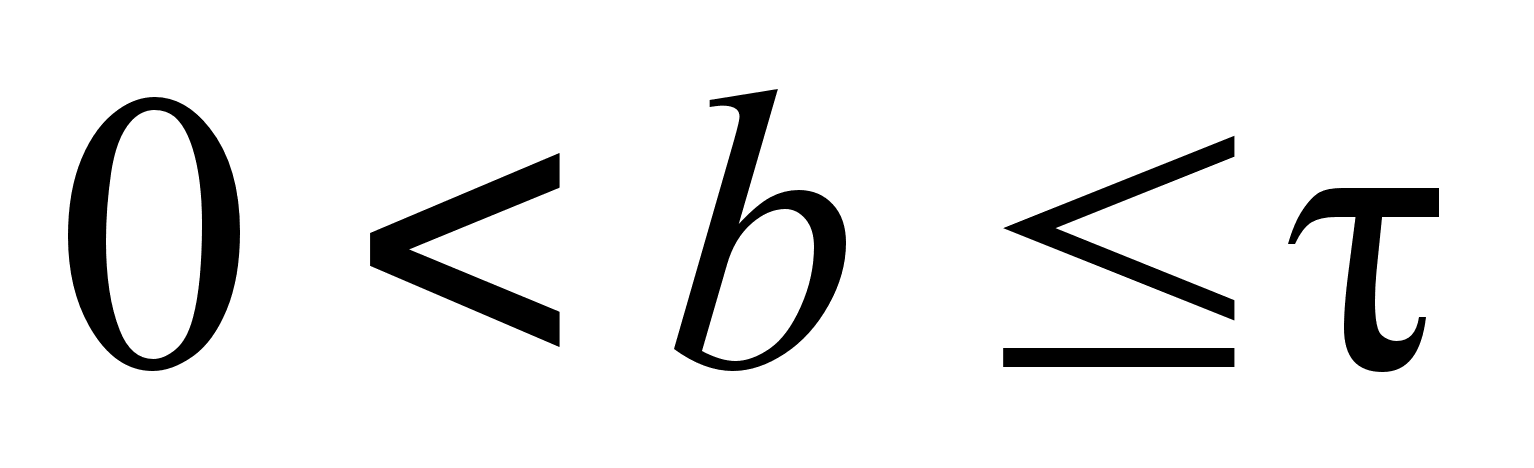 ).
).Если
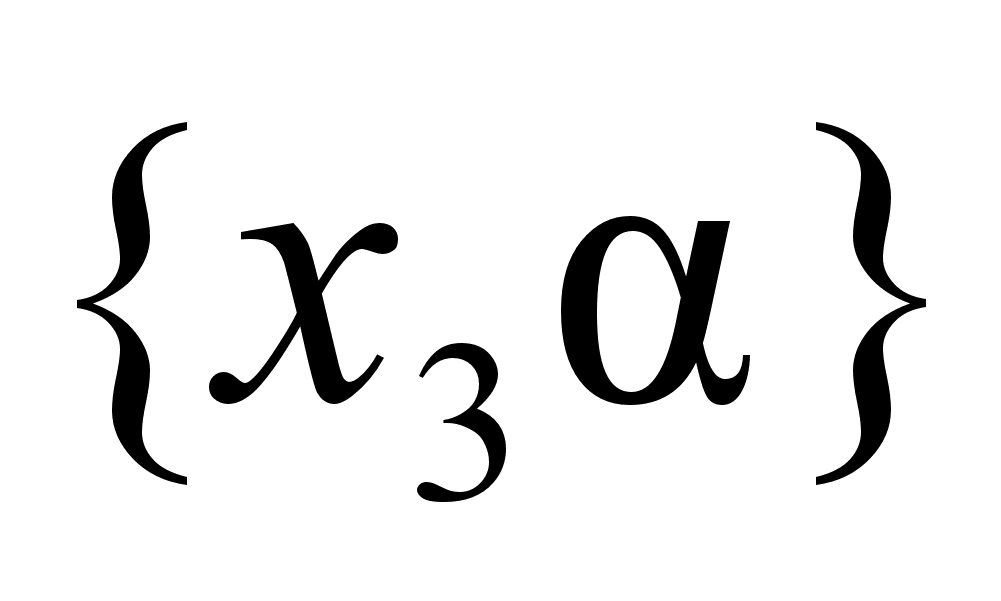 и
1 принадлежат
одному промежутку,
то
и
1 принадлежат
одному промежутку,
то
![]()
Пусть
в таком случае
![]() ,
,
![]() .
Очевидно, и
здесь
.
Очевидно, и
здесь
![]() ,
так что
,
так что
![]() ,
,
![]() ).
).
Теорема доказана.
Рассмотрим пример применения теоремы Дирихле.
Найти
рациональное
приближение
![]() к
к
![]() с точностью
до
с точностью
до
![]() .
.
Решение:
Разложим
![]() в цепную дробь.
в цепную дробь.
![]() =2
=2
![]() -2
-2
![]()
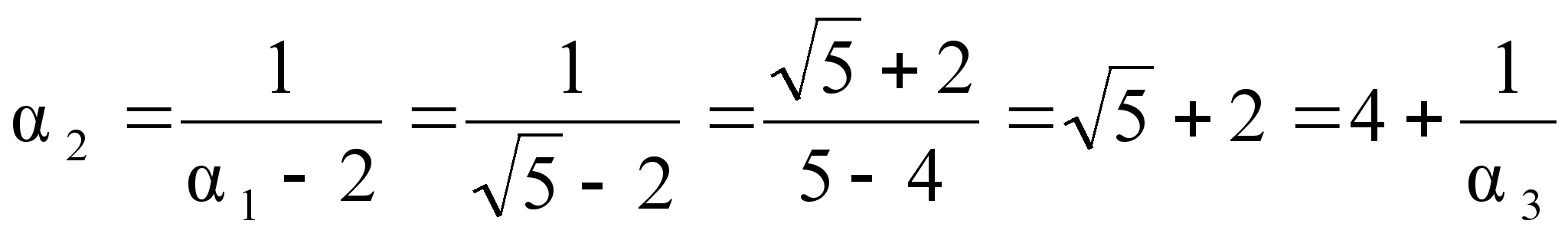
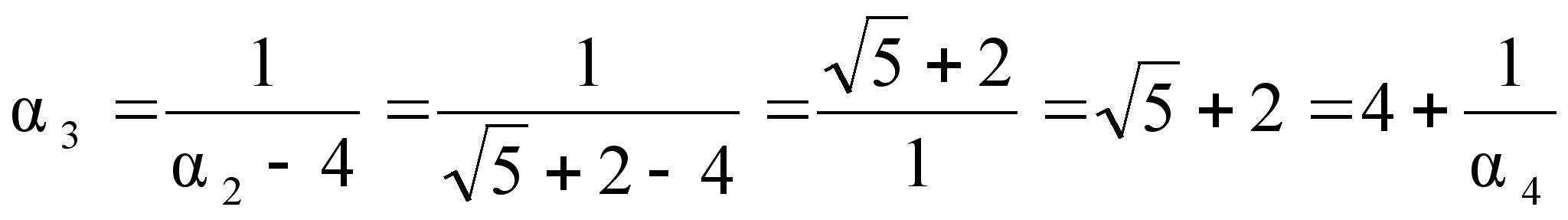
![]()
…
![]() =(2,
4, 4, 4, …)=(2,(4)).
=(2,
4, 4, 4, …)=(2,(4)).
Находим подходящие дроби:
|
2 |
4 |
4 |
4 |
4 |
4 |
… | |
|
|
2 |
9 |
38 |
161 |
682 |
… | … |
|
|
1 |
4 |
17 |
72 |
305 |
1929 |
… |
Наибольший
знаменатель,
меньший чем
100, при
![]() =305.
Искомая дробь
равна
=305.
Искомая дробь
равна
![]() ;
;
![]() .
.
Подходящие дроби как наилучшие приближения.
Приближение подходящей дробью дает большую точность при значительно меньшем знаменателе, чем приближение десятичной дробью. Покажем это.
Округляя
десятичное
выражение
действительного
![]() до n–го
знака после
запятой, мы тем
самым представляем
до n–го
знака после
запятой, мы тем
самым представляем
![]() приближенно
дробью
приближенно
дробью
![]() со знаменателем
со знаменателем
![]() ,
причем погрешность
,
причем погрешность
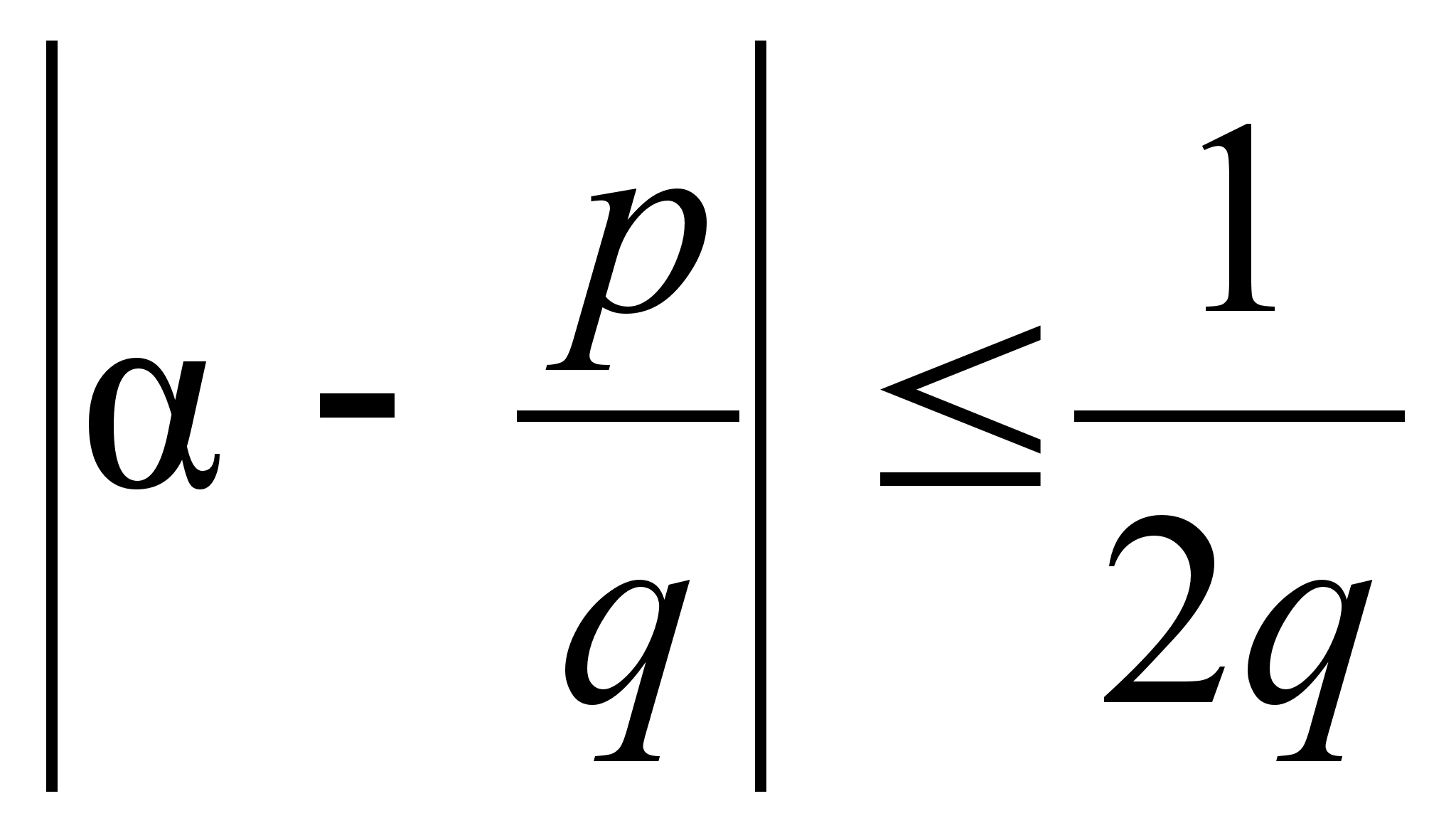 ,
если же
,
если же
![]() подходящая
дробь к
подходящая
дробь к
![]() ,
то
,
то
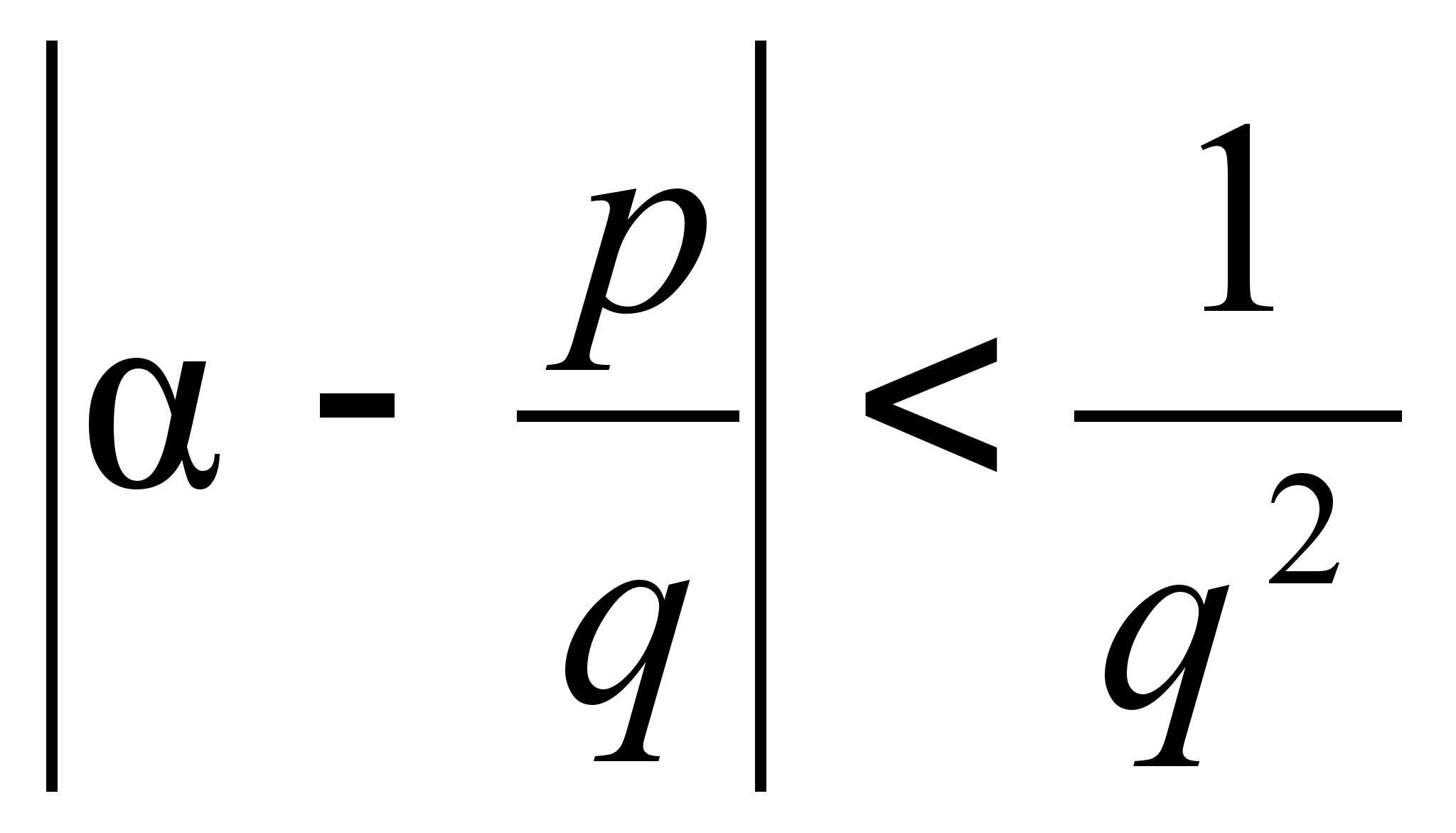 ,
так что при
сколько-нибудь
значительном
q
величина
,
так что при
сколько-нибудь
значительном
q
величина
![]() во много раз
меньше, чем
во много раз
меньше, чем
![]() .
.
Пример:
Десятичное
выражение числа
![]() в виде рациональной
дроби со знаменателем
в виде рациональной
дроби со знаменателем
![]() имеет вид
имеет вид
![]() .
Если же
.
Если же
![]() разложить в
цепную дробь,
получается
разложить в
цепную дробь,
получается
![]() =(3,
7, 15, …);
=(3,
7, 15, …);
![]()
Наибольшей
подходящей
дробью для
![]() со знаменателем
со знаменателем
![]() является число
является число
![]() ,
известное уже
Архимеду, причем
,
известное уже
Архимеду, причем
![]() .
Итак, мы получили,
что приближение
подходящей
дробью дает
большую точность,
чем приближение
десятичной
дробью.
.
Итак, мы получили,
что приближение
подходящей
дробью дает
большую точность,
чем приближение
десятичной
дробью.
Это
объясняется
тем, что знаменатели
подходящих
дробей определяются
арифметической
природой
изображаемого
числа, а знаменатели
же приближающих
десятичных
дробей не могут
быть иными, как
только
![]() .
.
Теорема:
Если рациональное
число
![]() ближе к действительному
числу
ближе к действительному
числу
![]() ,
чем его подходящая
дробь
,
чем его подходящая
дробь
![]() ,
где k>1,
то
,
где k>1,
то
![]() ,
то есть если
,
то есть если
![]()
![]() ,
то
,
то
![]() .
.
Доказательство:
Рассмотрим
случай, когда
![]() (иначе теряет
смысл). Тогда
(иначе теряет
смысл). Тогда
![]() всегда лежит
между любыми
двумя последующими
подходящими
дробями так,
что для
k>1
всегда лежит
между любыми
двумя последующими
подходящими
дробями так,
что для
k>1
![]() всегда лежит
между
всегда лежит
между
![]() и
и
![]() ,
причем ближе
к
,
причем ближе
к
![]() ,
чем к
,
чем к
![]() .
Поэтому, если
.
Поэтому, если
![]() ближе к
ближе к
![]() ,
чем
,
чем
![]() ,
то оно находится
между
,
то оно находится
между
![]() и
и
![]() .
В случае четного
.
В случае четного
![]() можно записать
можно записать
![]()
![]()
![]() (в случае нечетного
k
доказательство
существенно
не меняется),
откуда
(в случае нечетного
k
доказательство
существенно
не меняется),
откуда
![]() ,
или
,
или
![]() ,
,![]()
![]()
![]() ,
откуда, домножая
неравенство
на
,
откуда, домножая
неравенство
на
![]() ,
получаем
,
получаем
![]() .
Так как
.
Так как
![]() – число целое
и положительное,
то из предыдущего
равенства
следует
– число целое
и положительное,
то из предыдущего
равенства
следует
![]() ,
что и требовалось
доказать.
,
что и требовалось
доказать.
Попутно
мы установили,
что любая
рациональная
дробь
![]() ,
принадлежащая
интервалу
,
принадлежащая
интервалу
![]() ,
k>1,
имеет знаменатель
,
k>1,
имеет знаменатель
![]() .
Для
k=1
теорема неверна:
.
Для
k=1
теорема неверна:
![]() может
оказаться ближе
к
может
оказаться ближе
к
![]() ,
чем его подходящая
дробь
,
чем его подходящая
дробь
![]() ,
хотя
,
хотя
![]() .
.
Доказанная теорема приводит нас к следующему определению:
Рациональную
дробь
![]() называют наилучшим
приближением
действительного
называют наилучшим
приближением
действительного
![]() ,
если любая
более близкая
к
,
если любая
более близкая
к
![]() рациональная
дробь
рациональная
дробь
![]() имеет больший
знаменатель,
чем
имеет больший
знаменатель,
чем
![]() ,
то есть если
из
,
то есть если
из
![]() следует d>b.
следует d>b.
Таким
образом, подходящие
дроби являются
наилучшими
приближениями,
например, Архимедово
число
![]() для
для
![]() является наилучшим
приближением.
является наилучшим
приближением.
Ранее
мы доказали,
что для оценки
погрешности
![]() ,
возникающей
при замене
любого действительного
,
возникающей
при замене
любого действительного
![]() его подходящей
дробью
его подходящей
дробью
![]() ,
можно пользоваться
неравенством
,
можно пользоваться
неравенством
![]() .
Выразим этот
результат по
отношению к
действительному
иррациональному
.
Выразим этот
результат по
отношению к
действительному
иррациональному
![]() ,
имеющим бесконечное
множество
подходящих
дробей, следующим
образом: для
любого действительного
иррационального
,
имеющим бесконечное
множество
подходящих
дробей, следующим
образом: для
любого действительного
иррационального
![]() существует
при
c=1
бесконечное
множество
несократимых
дробей
существует
при
c=1
бесконечное
множество
несократимых
дробей
![]() таких, что
таких, что
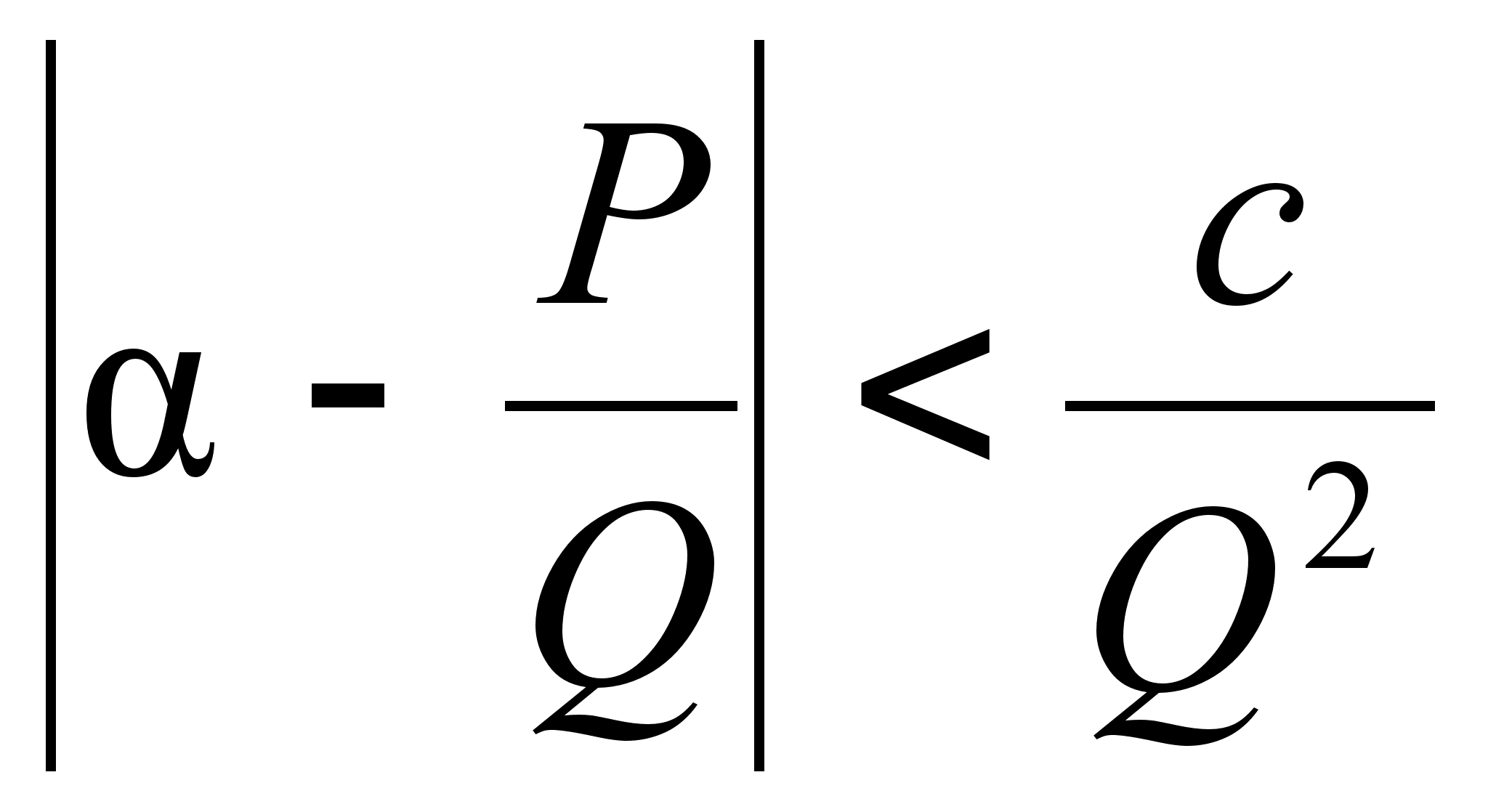 (1).
(1).
Такими
дробями являются,
например, все
подходящие
дроби для
![]()
![]() .
.
Возникает
вопрос: При
каких меньших
значениях
c
(чем c=1)
существует
для любого
действительного
иррационального
![]() бесконечное
множество
(несократимых)
рациональных
приближений
бесконечное
множество
(несократимых)
рациональных
приближений
![]() ,
погрешность
которых
,
погрешность
которых
![]() .
.
Теорема:
Для любого
действительного
иррационального
числа
![]() существует
при
существует
при
![]() бесконечное
множество
несократимых
рациональных
дробей
бесконечное
множество
несократимых
рациональных
дробей
![]() таких, что
таких, что
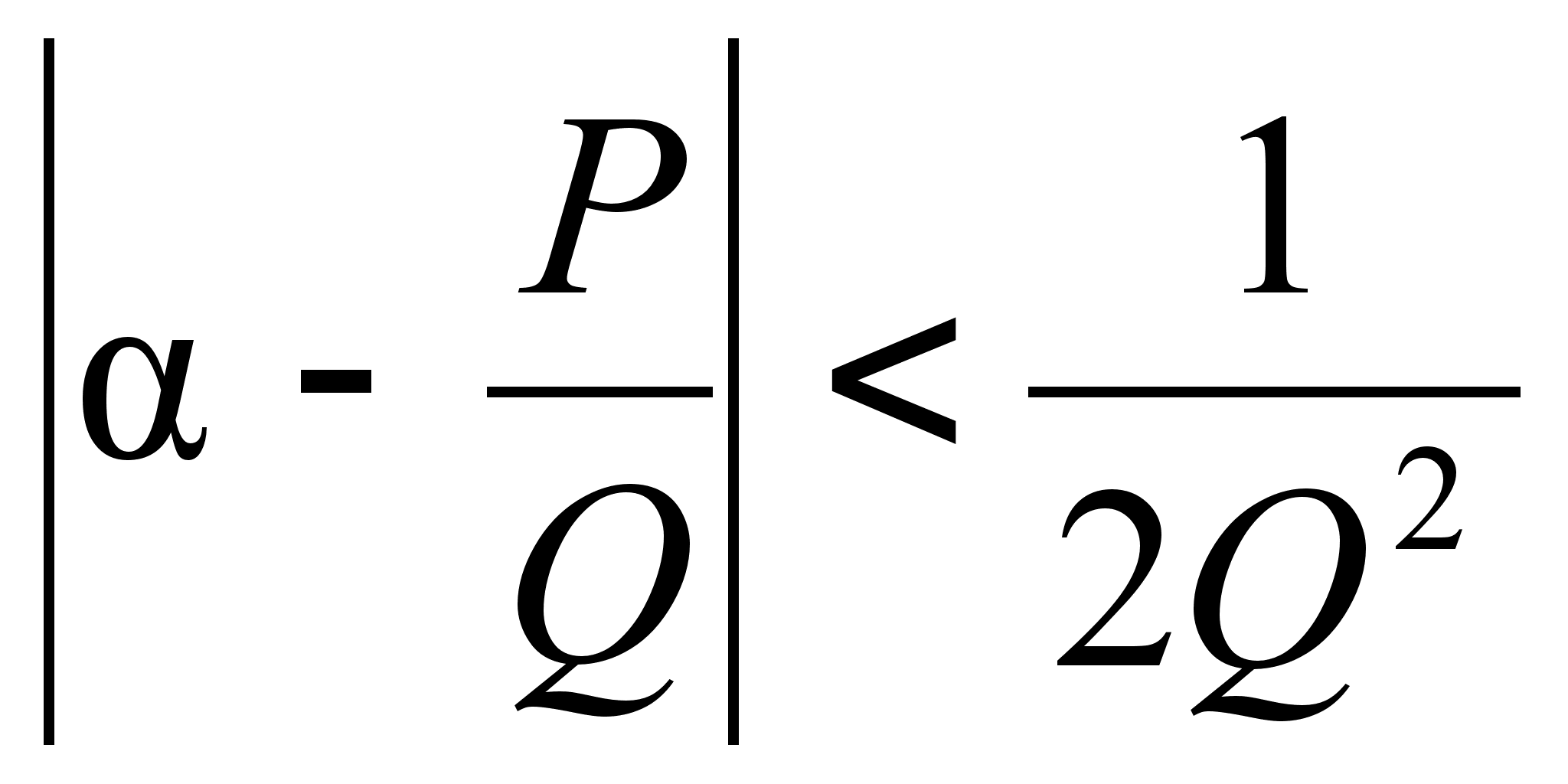 (
(![]() ).
Такими рациональными
дробями могут
быть только
подходящие
дроби к
).
Такими рациональными
дробями могут
быть только
подходящие
дроби к
![]() .
.
Доказательство:
Докажем первую
часть теоремы.
Рассмотрим
две последующие
подходящие
дроби к
![]()
![]() и
и
![]() .
Допустим, что
ни одна из этих
дробей не
удовлетворяет
неравенству
(
.
Допустим, что
ни одна из этих
дробей не
удовлетворяет
неравенству
(![]() ).
Тогда имеем:
).
Тогда имеем:
![]() ,
,
![]() .
Отсюда
.
Отсюда
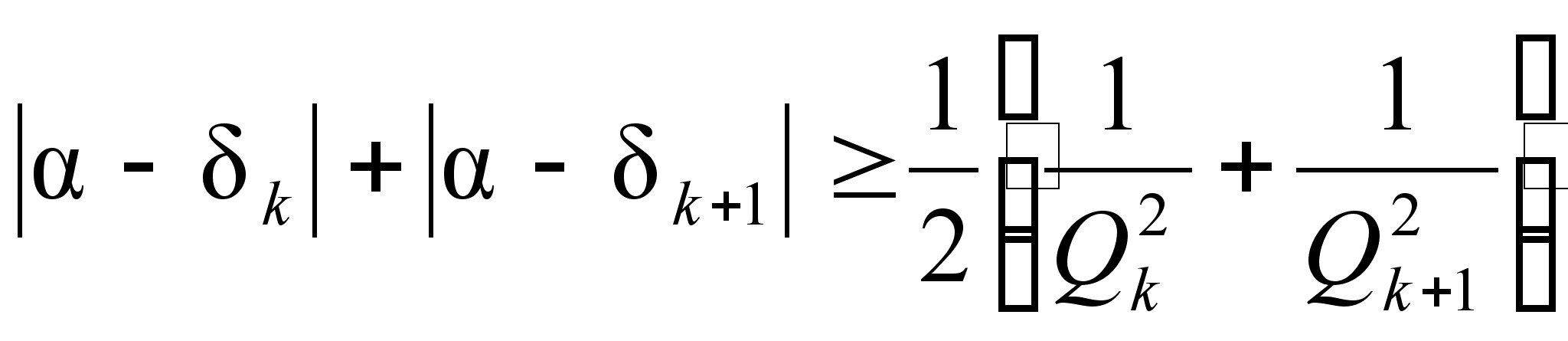 .
.
Но
так как
![]() лежит между
лежит между
![]() и
и
![]() ,
то
,
то
![]()
![]() ,
вследствие
чего
,
вследствие
чего
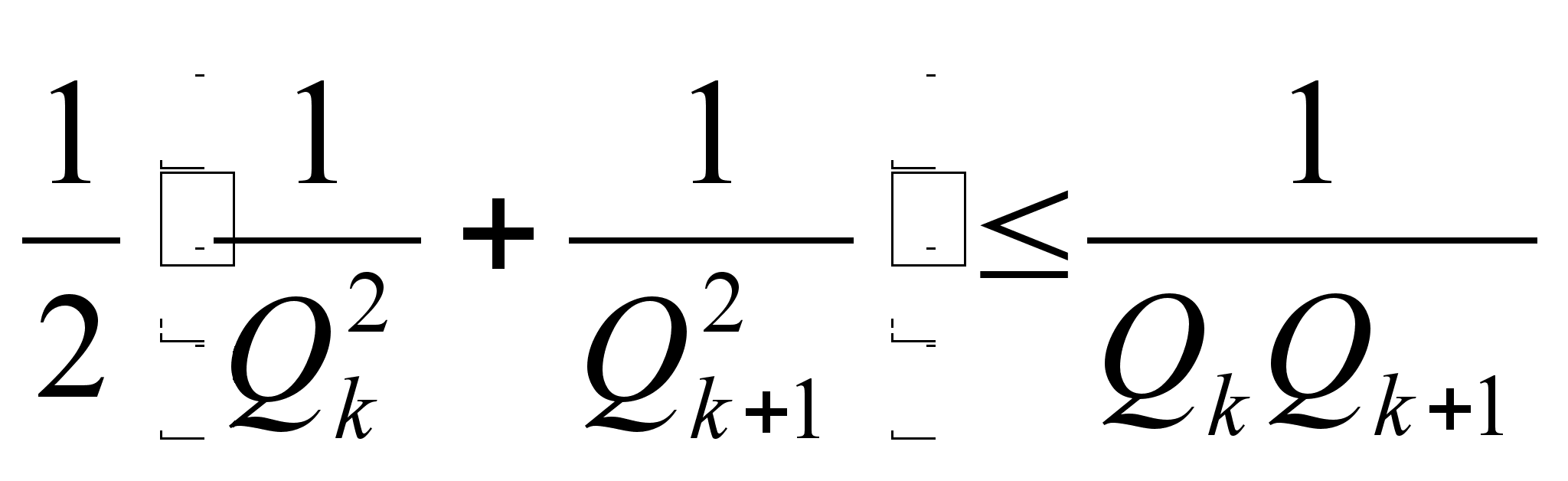 ,
или
,
или
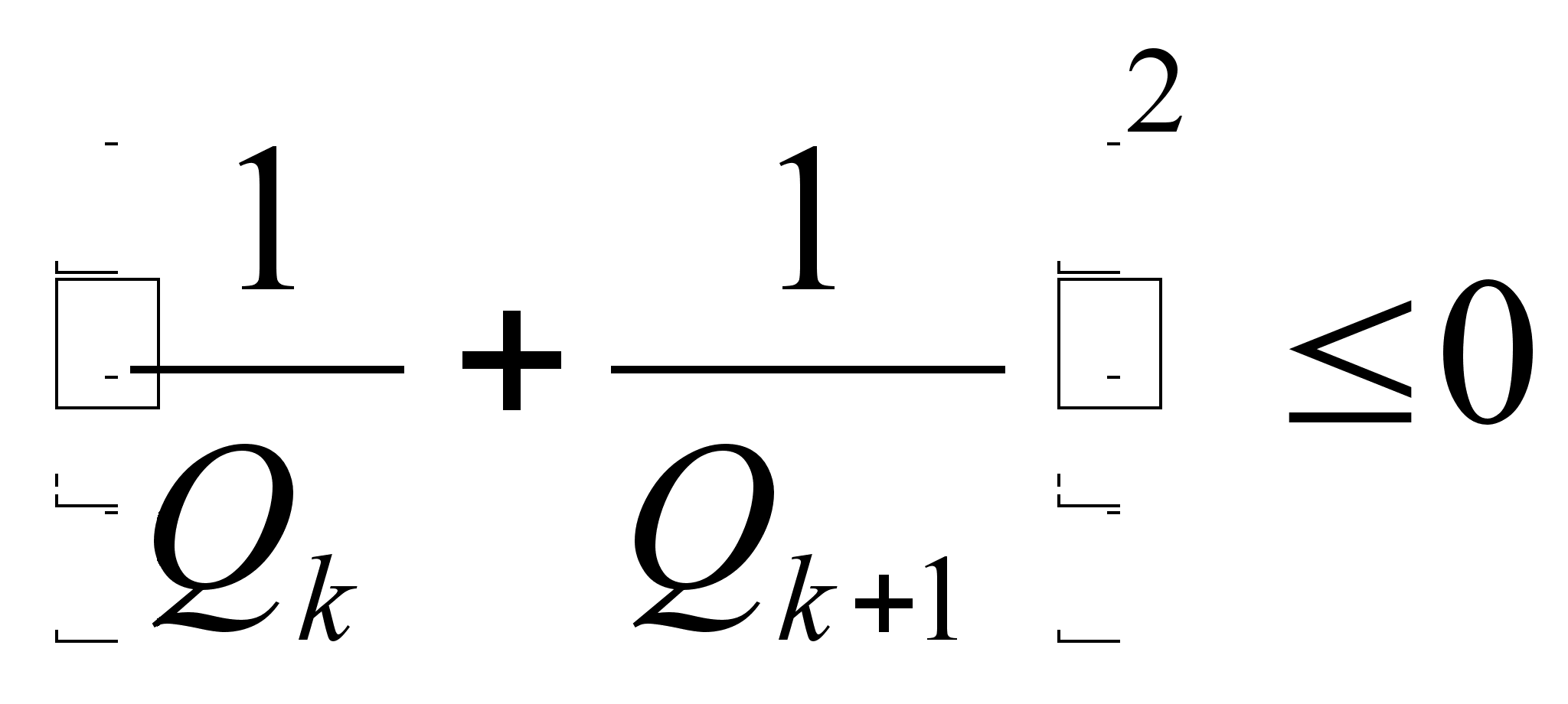 ,
а это для
k>1
невозможно.
Мы пришли к
противоречию,
значит наше
допущение
неверно, а верно
то, что требуется
доказать.
,
а это для
k>1
невозможно.
Мы пришли к
противоречию,
значит наше
допущение
неверно, а верно
то, что требуется
доказать.
Для
доказательства
второй части
теоремы докажем
достаточный
признак подходящей
дроби к действительному
числу
![]() :
если
:
если
![]() ,
где Q>0,
несократимая
дробь и для
действительного
,
где Q>0,
несократимая
дробь и для
действительного
![]() имеет место
неравенство
(
имеет место
неравенство
(![]() ),
то
),
то
![]() является подходящей
дробью к
является подходящей
дробью к
![]() .
.
Доказательство:
Покажем, что
если
![]() =(
=(![]() )=
)=![]() (
(![]() удовлетворяет
условию теоремы)
подходящая
дробь к
удовлетворяет
условию теоремы)
подходящая
дробь к
![]() ,
то соответствующее
остаточное
число
,
то соответствующее
остаточное
число
![]() разложения
данного
разложения
данного
![]() в цепную дробь
окажется >1.
Действительно,
в цепную дробь
окажется >1.
Действительно,
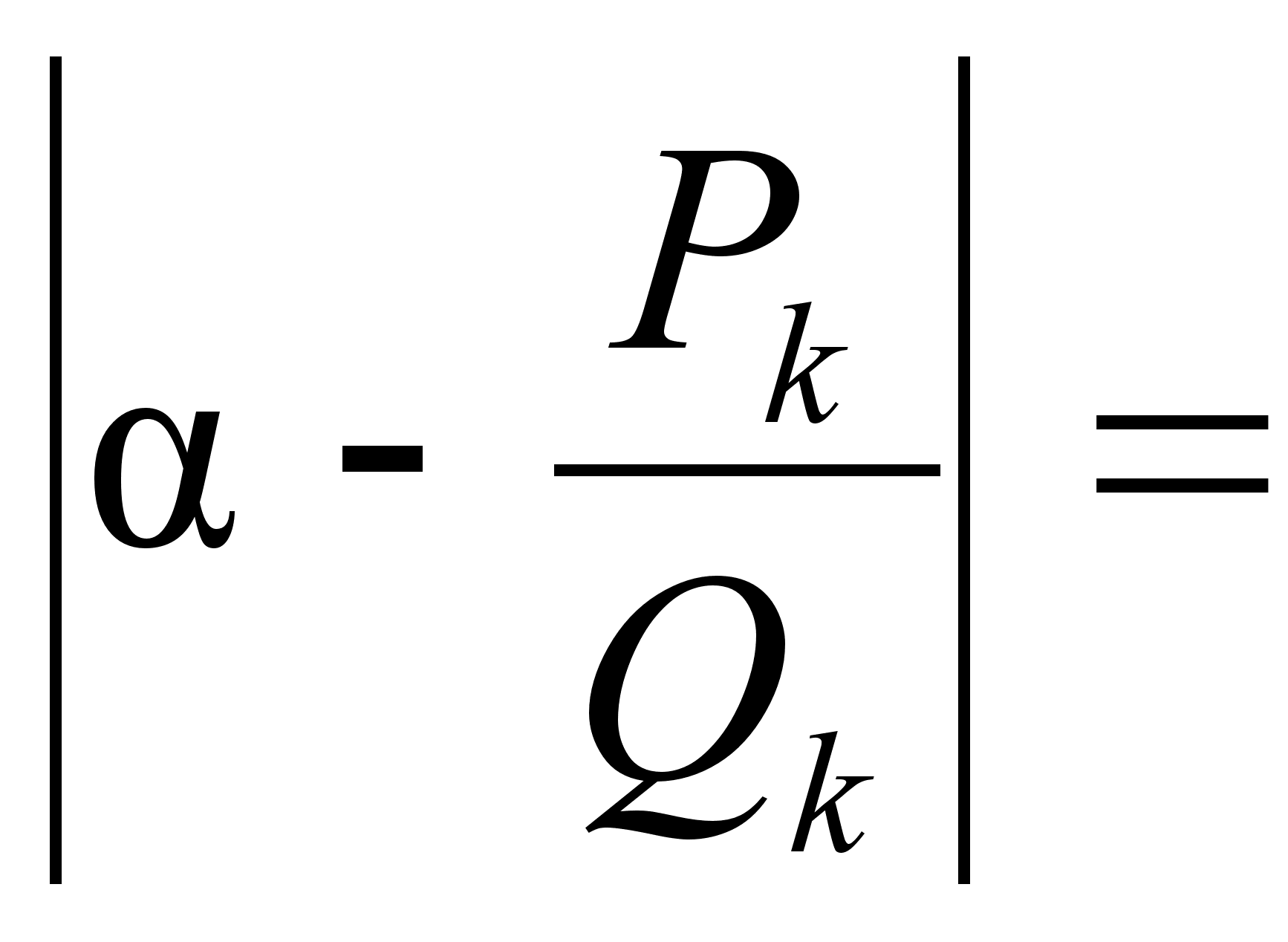
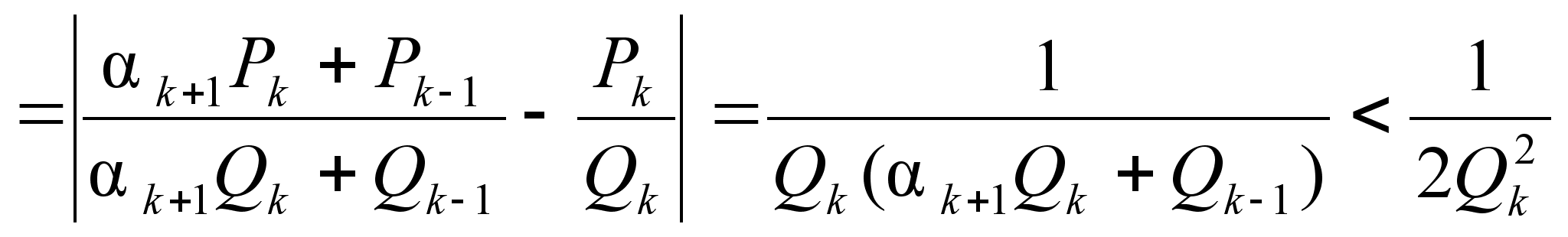 ,
откуда следует
,
откуда следует
![]() ,
так как
,
так как
![]() .
.
Теорема доказана полностью.
Достаточный
признак подходящей
дроби не является
ее необходимым
признаком;
могут существовать
подходящие
дроби для
![]() ,
которые ему
не удовлетворяют.
,
которые ему
не удовлетворяют.
Крайнюю возможность уменьшения c в указанном раньше смысле выражает теорема Гурвица-Бореля:
Теорема:
Для любого
действительного
иррационального
числа
![]() существует
при
существует
при
![]() бесконечное
множество
несократимых
рациональных
дробей
бесконечное
множество
несократимых
рациональных
дробей
![]() таких, что
выполняется
неравенство
(1),
то есть неравенство
таких, что
выполняется
неравенство
(1),
то есть неравенство
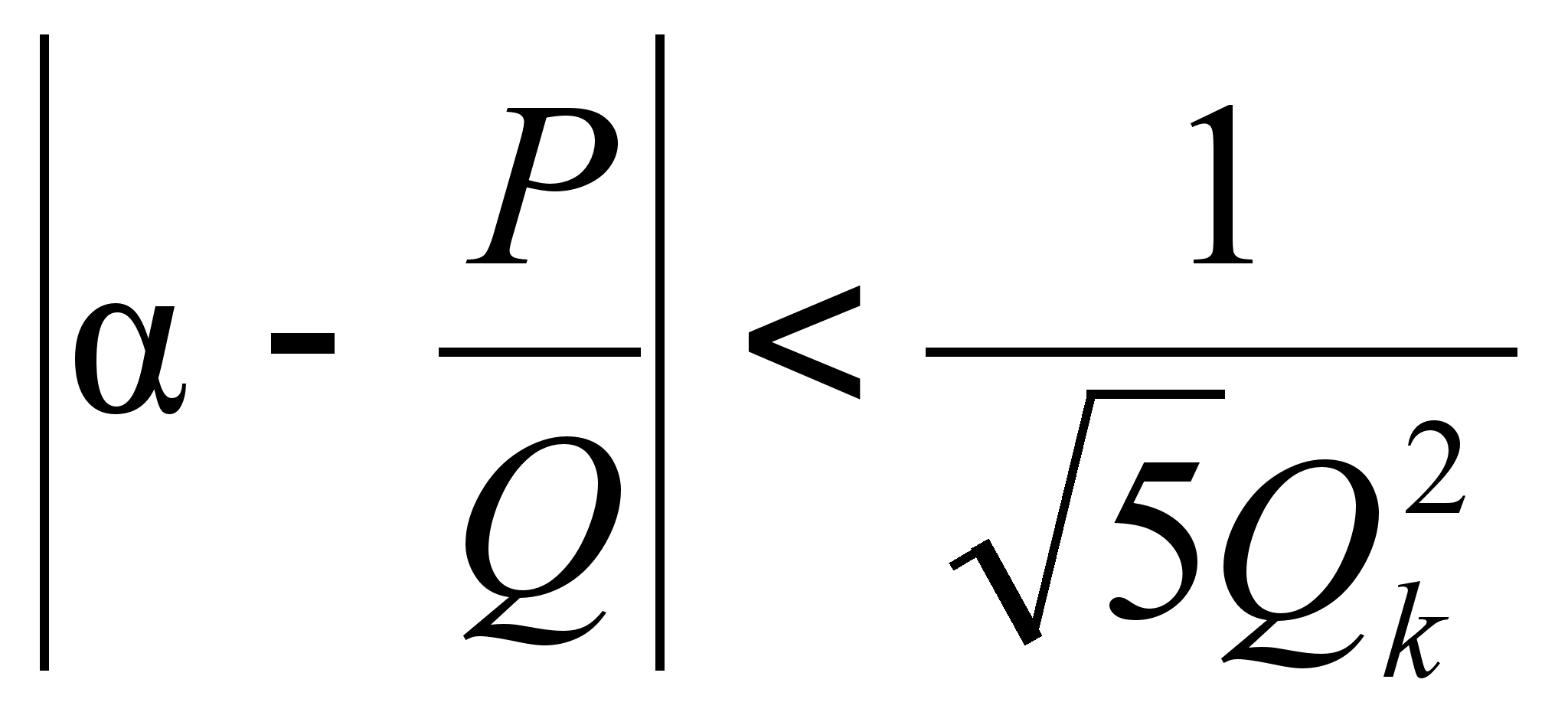 ,
(
,
(![]() )
)
если
же
![]() ,
то существуют
такие действительные
иррациональные
,
то существуют
такие действительные
иррациональные
![]() ,
для которых
неравенство
(1) имеет
не более конечного
числа рациональных
решений
,
для которых
неравенство
(1) имеет
не более конечного
числа рациональных
решений
![]() .
.
Доказательство:
Докажем первую
часть. Разложим
![]() в цепную дробь.
Мы докажем, что
из трех любых
соседних подходящих
дробей
в цепную дробь.
Мы докажем, что
из трех любых
соседних подходящих
дробей
![]() ,
i=k,
k+1,
k+2
по
крайней мере
одна удовлетворяет
условию
,
i=k,
k+1,
k+2
по
крайней мере
одна удовлетворяет
условию
![]() .
Доказательство
этого утверждения
будем вести
методом от
противного.
Предположим,
что для каких-либо
трех соседних
подходящих
дробей выполняются
неравенства:
.
Доказательство
этого утверждения
будем вести
методом от
противного.
Предположим,
что для каких-либо
трех соседних
подходящих
дробей выполняются
неравенства:
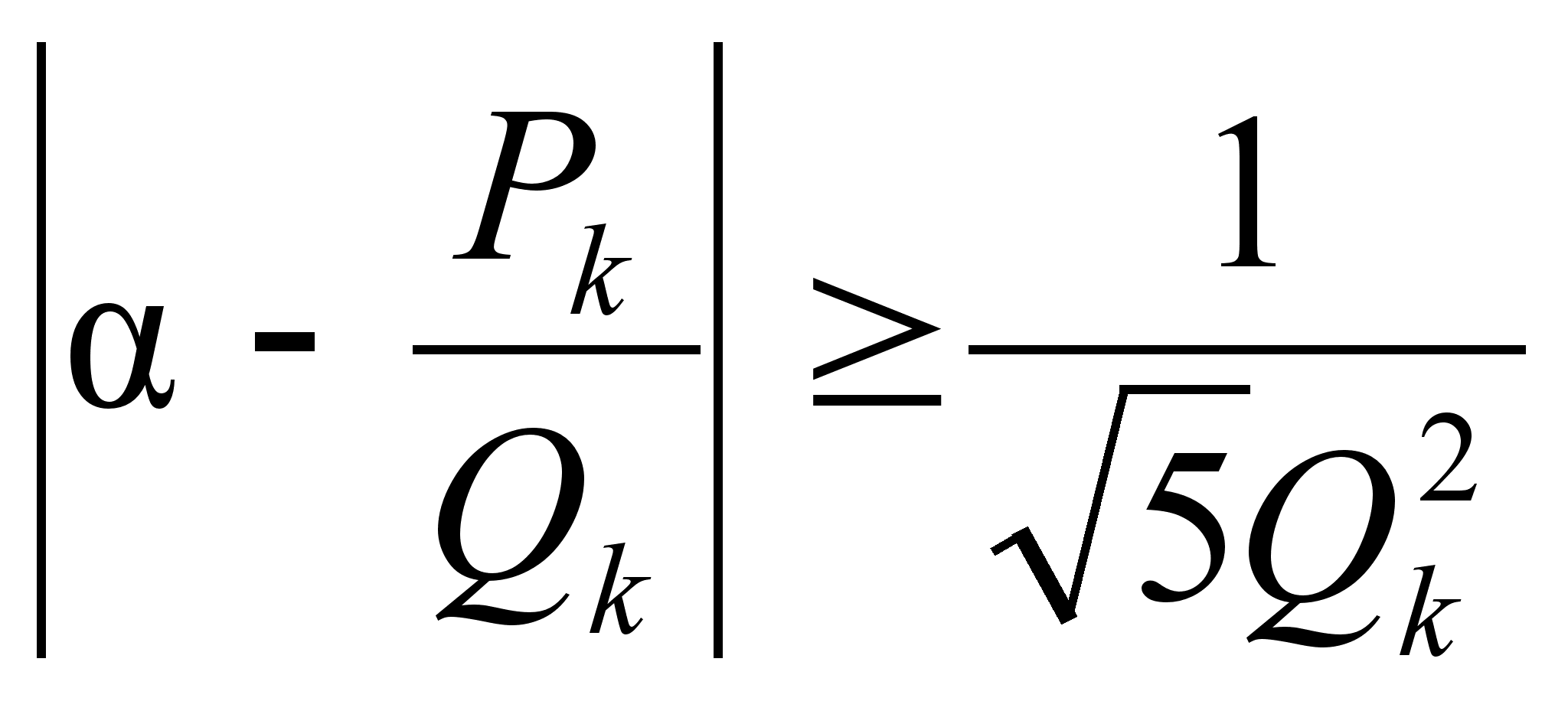 ,
,
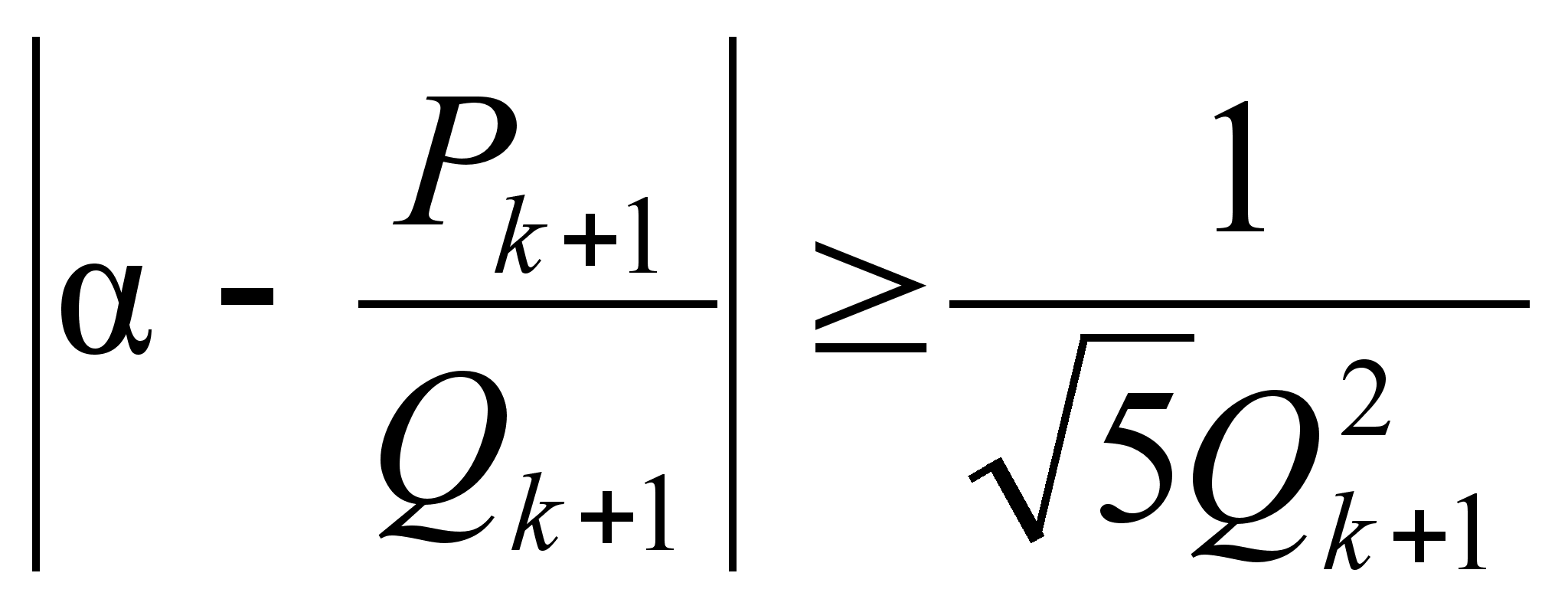 ,
,
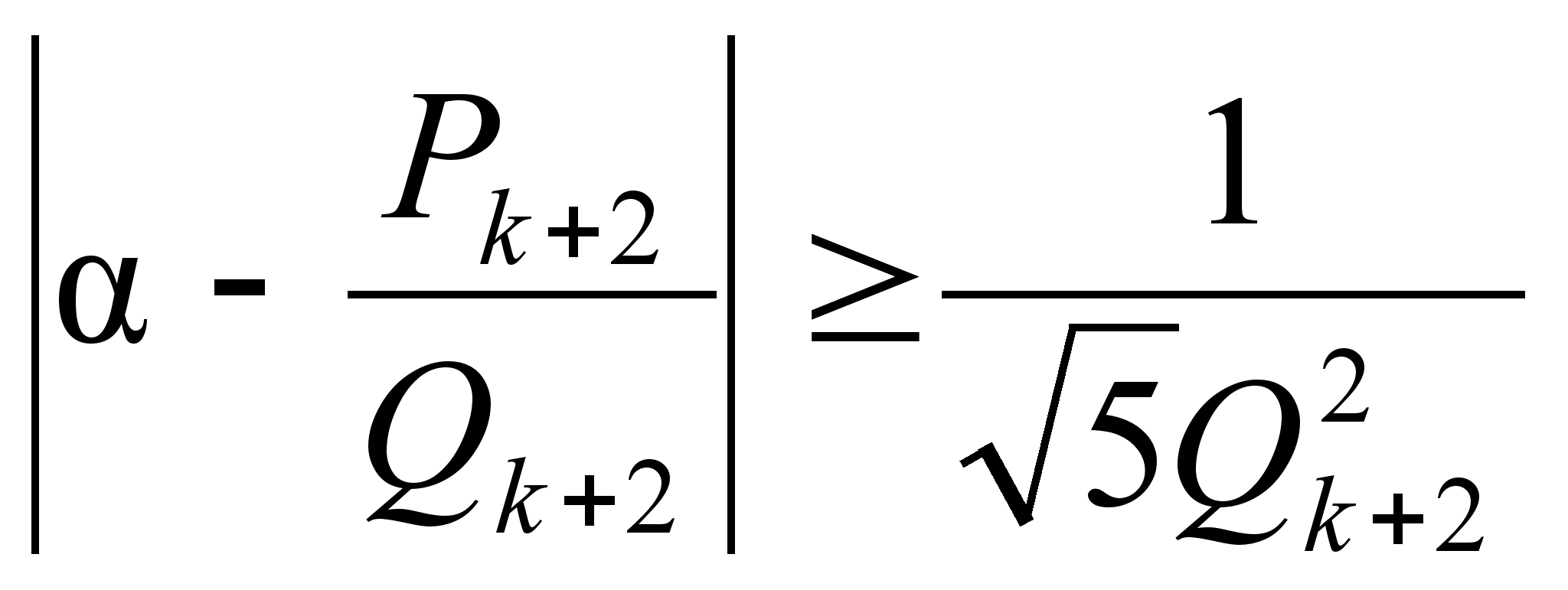 (2)
(2)
![]() и
и
![]() расположены
по разные стороны
от
расположены
по разные стороны
от
![]() и поэтому при
нечетном
k
из
(2) следует
и поэтому при
нечетном
k
из
(2) следует
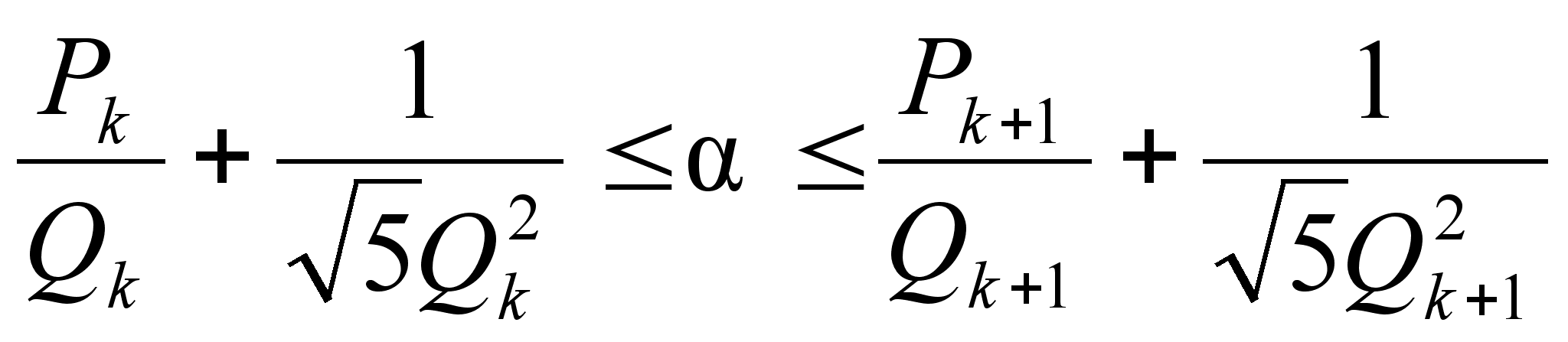 ,
,
а
при четном:
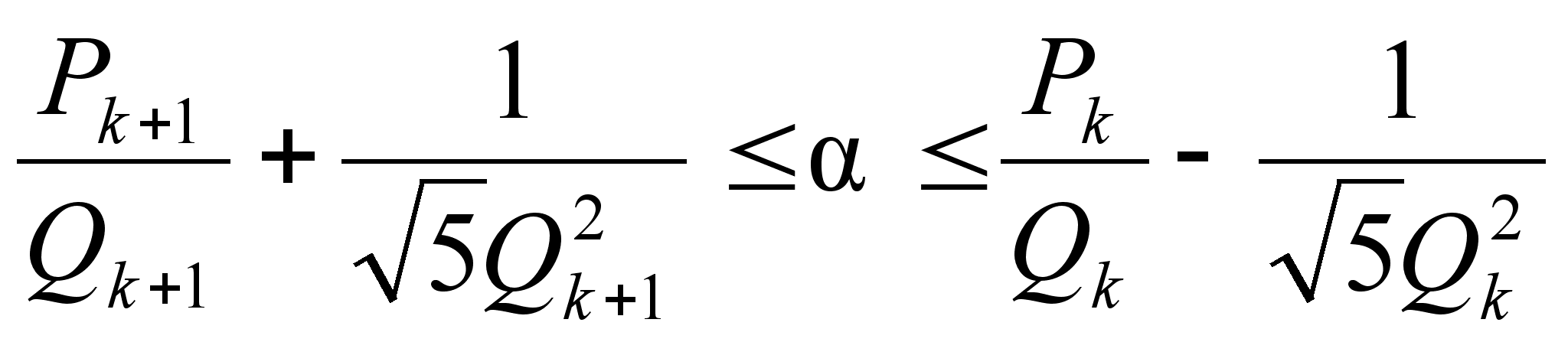 ,
так что и в том,
и в другом случае
имеем:
,
так что и в том,
и в другом случае
имеем:
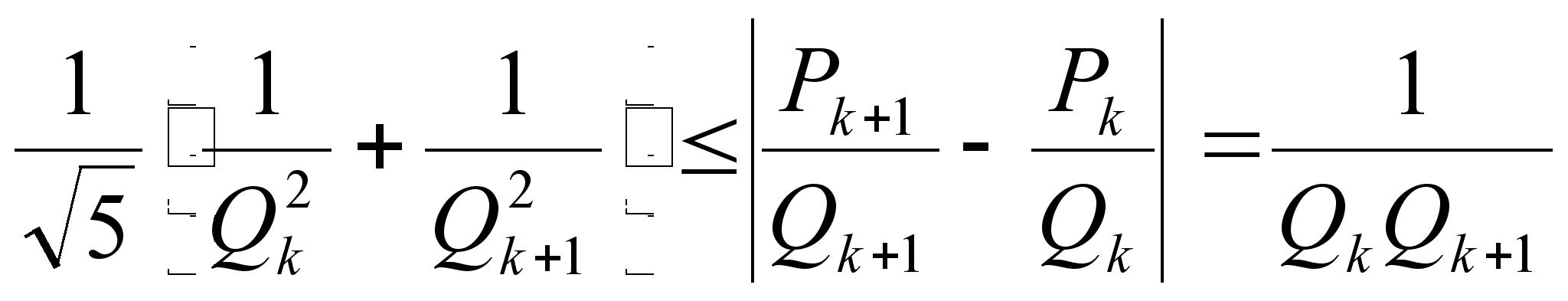
,
или, умножая
на
![]() и перенося все
члены в одну
сторону
и перенося все
члены в одну
сторону
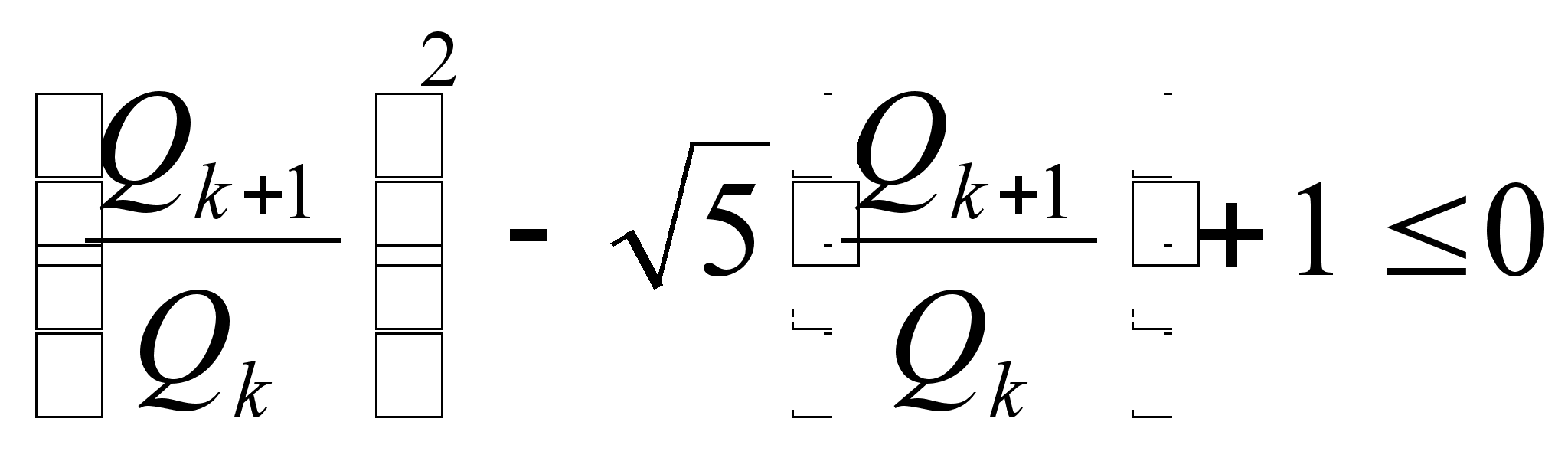 ,
то есть
,
то есть
 ,
,
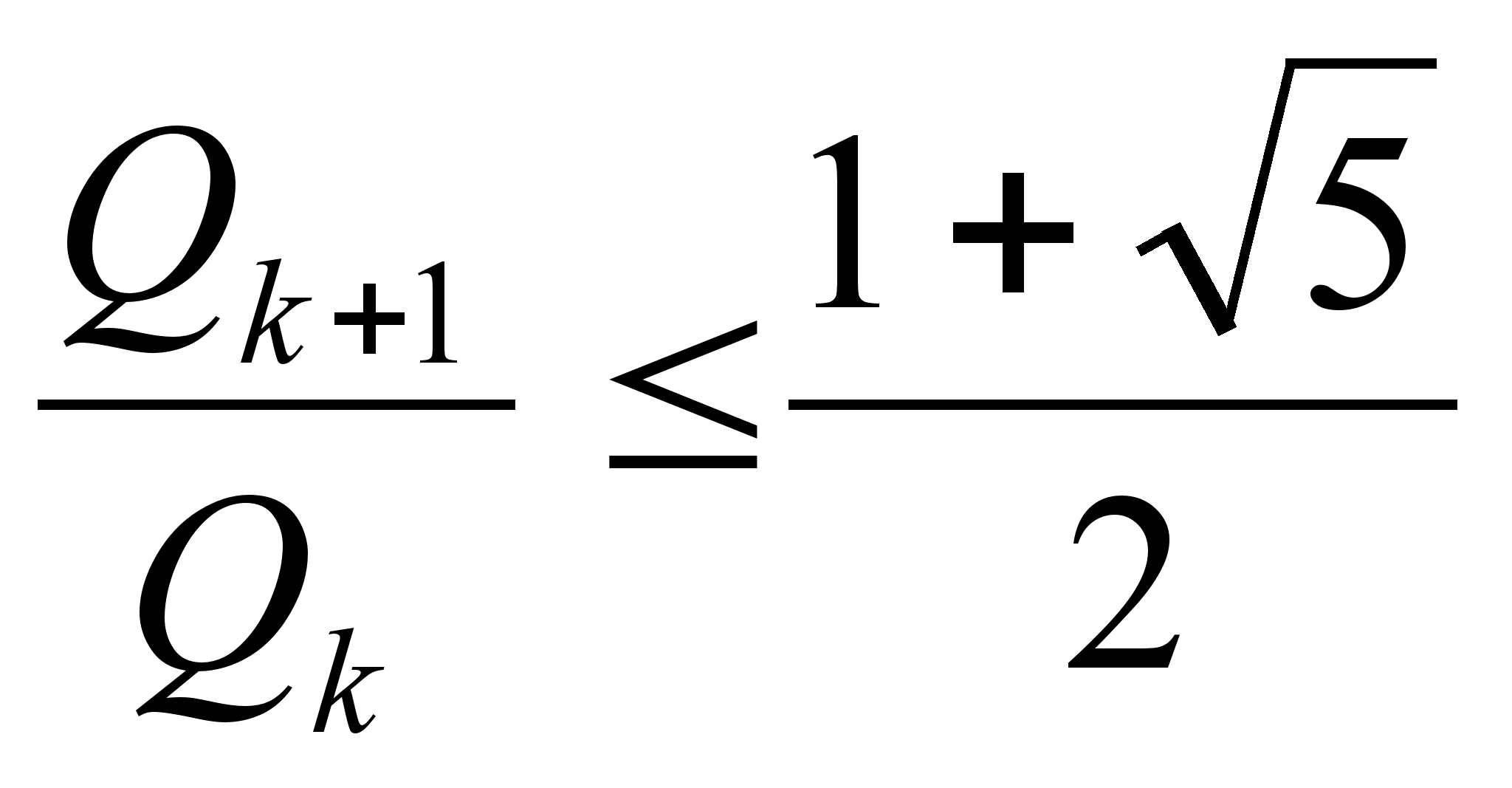 ,
или, поскольку
,
или, поскольку
![]() и
и
![]() целые,
целые,
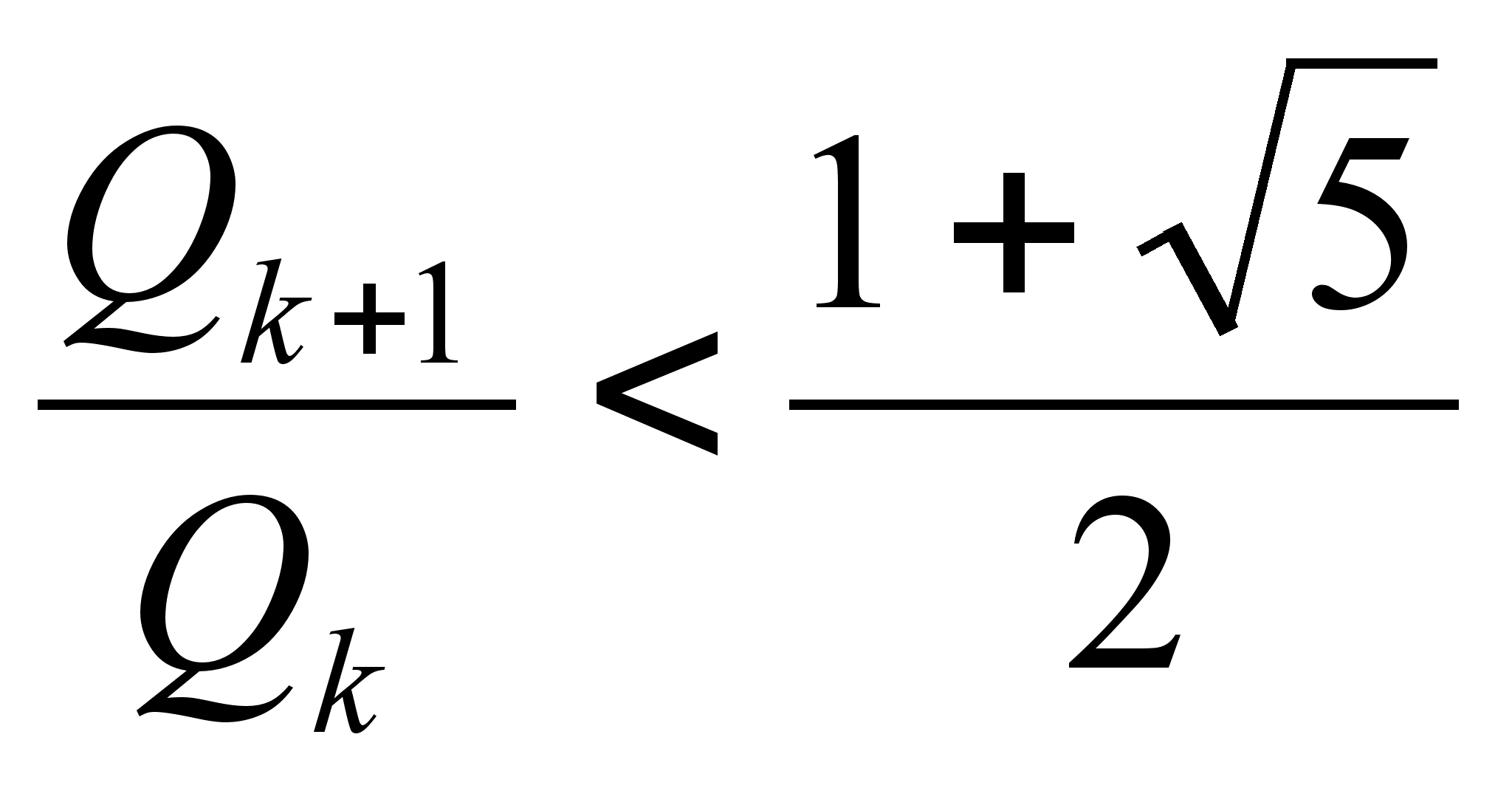 .
(3)
.
(3)
Так
как
![]() и
и
![]() также расположены
по разные стороны
от
также расположены
по разные стороны
от
![]() ,
из
(2) аналогично
получаем:
,
из
(2) аналогично
получаем:
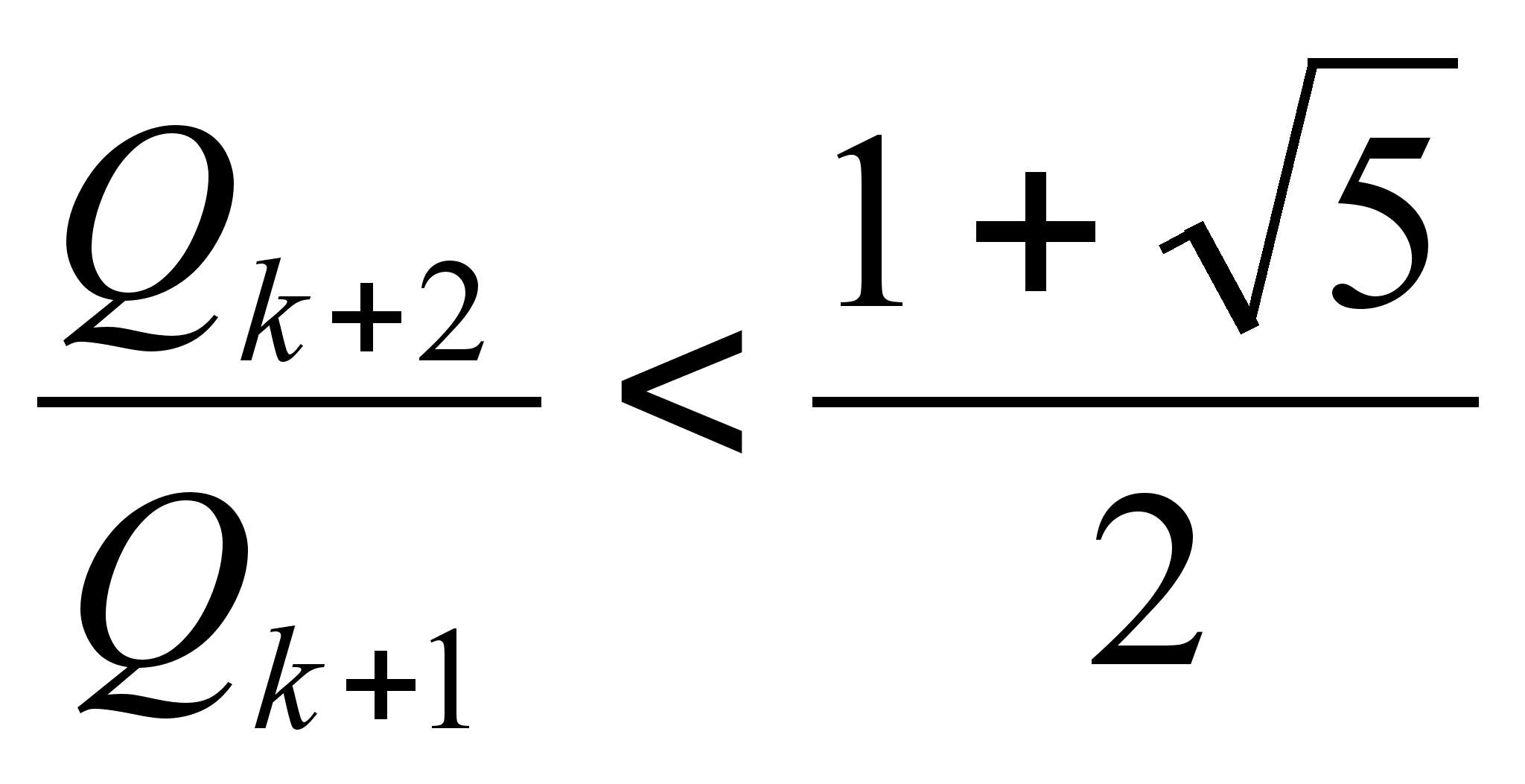 .
(4)
.
(4)
Пользуясь
еще тем, что
![]() из
(3) и
(4) получаем:
из
(3) и
(4) получаем:
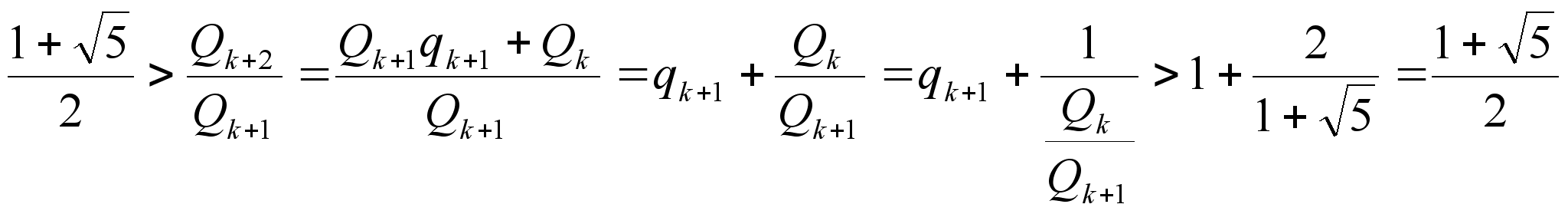 .
.
Предположение,
что выполнены
все три неравенства
(2),
привело нас
к противоречию,
поэтому по
крайней мере
для одной из
трех подходящих
дробей
![]() ,
,
![]() ,
,
![]() ,
взятой в качестве
,
взятой в качестве
![]() ,
должно выполняться
неравенство
(
,
должно выполняться
неравенство
(![]() ).
).
Придавая
k
различные
значения, получим
бесконечное
множество
дробей, удовлетворяющих
неравенству
(![]() ).
).
Докажем вторую часть.
Предположим,
что при
![]() ,
,
![]() неравенство
(1)
неравенство
(1)
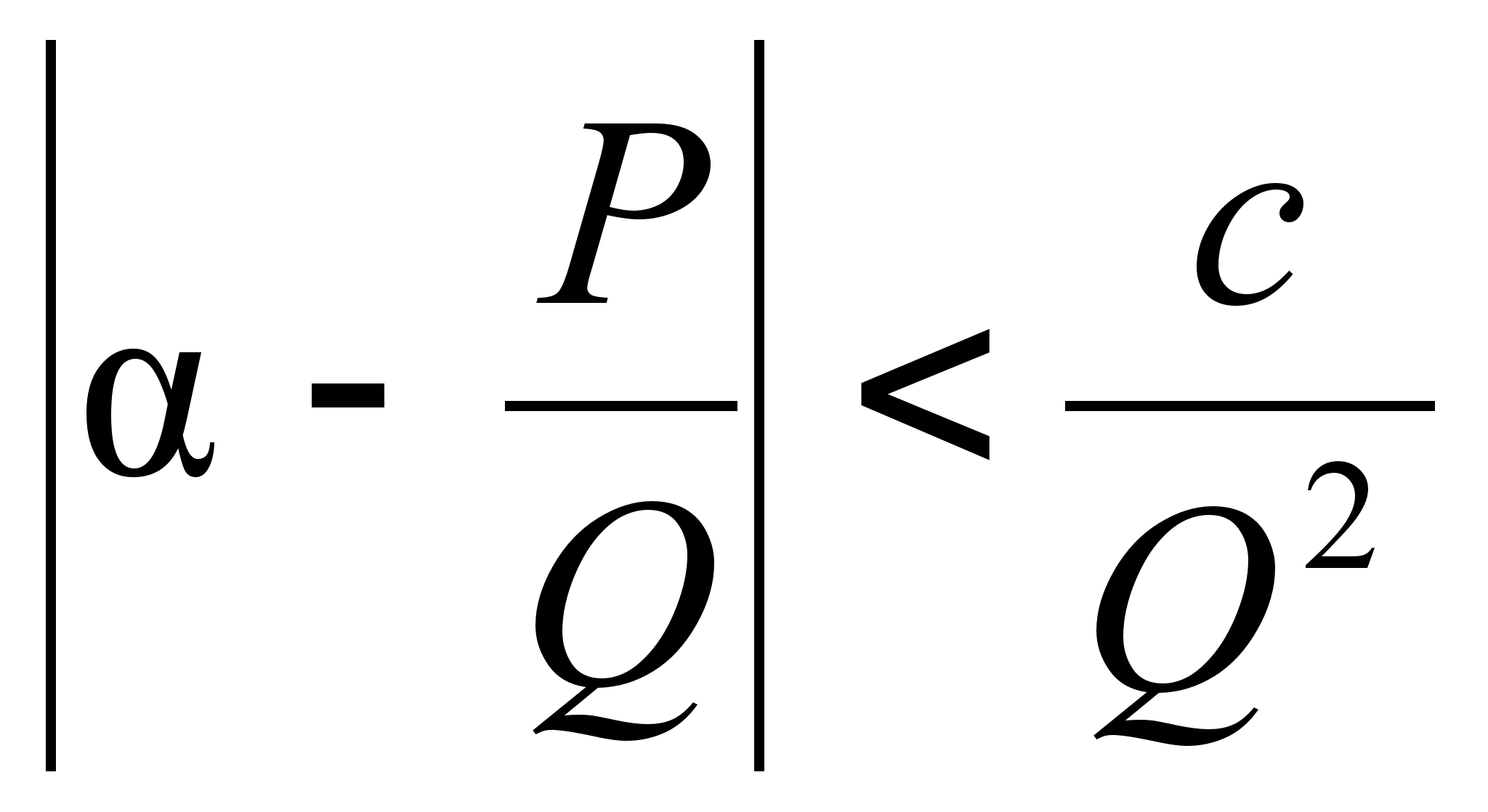 удовлетворяется
для бесконечного
множества
рациональных
чисел
удовлетворяется
для бесконечного
множества
рациональных
чисел
![]() .
Тогда для каждой
такой дроби
неравенства
.
Тогда для каждой
такой дроби
неравенства
![]() ,
откуда, подставляя
значение
,
откуда, подставляя
значение
![]() ,
получаем
,
получаем
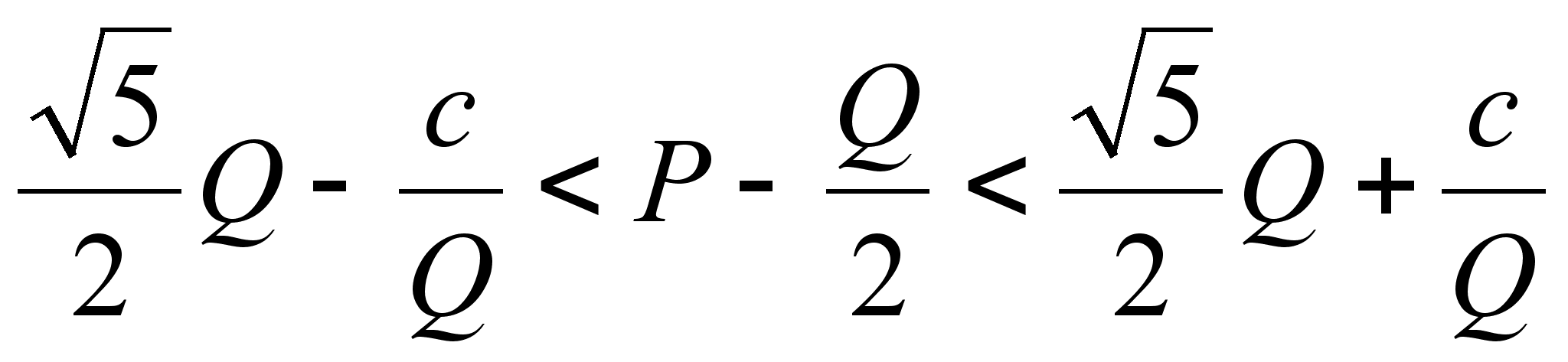 ,
а возводя в
квадрат, получаем:
,
а возводя в
квадрат, получаем:
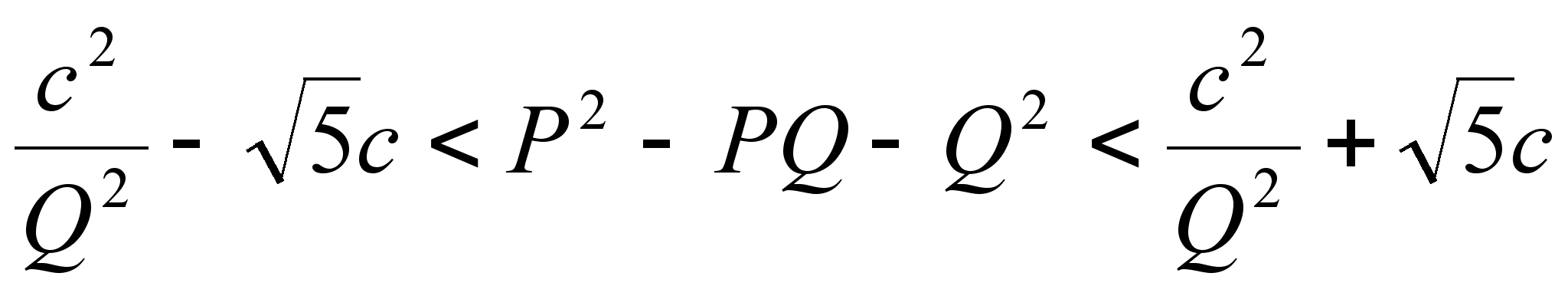 .
Так как
.
Так как
![]() ,
то при достаточно
большом
Q будем
иметь:
,
то при достаточно
большом
Q будем
иметь:
![]() и, следовательно,
целое число
и, следовательно,
целое число
![]() ,
,
![]() =
=![]() ,
что при целых
P
и
Q
не может иметь
места. Полученное
противоречие
показывает,
что неравенство
(1) может
иметь место
только для
конечного числа
рациональных
чисел
,
что при целых
P
и
Q
не может иметь
места. Полученное
противоречие
показывает,
что неравенство
(1) может
иметь место
только для
конечного числа
рациональных
чисел
![]() .
Теорема доказана
полностью.
.
Теорема доказана
полностью.
Эта теорема
была опубликована
Гурвицем в 1891
году. Тот факт,
что из трех
соседних подходящих
дробей по крайней
мере одна даст
приближение
вида
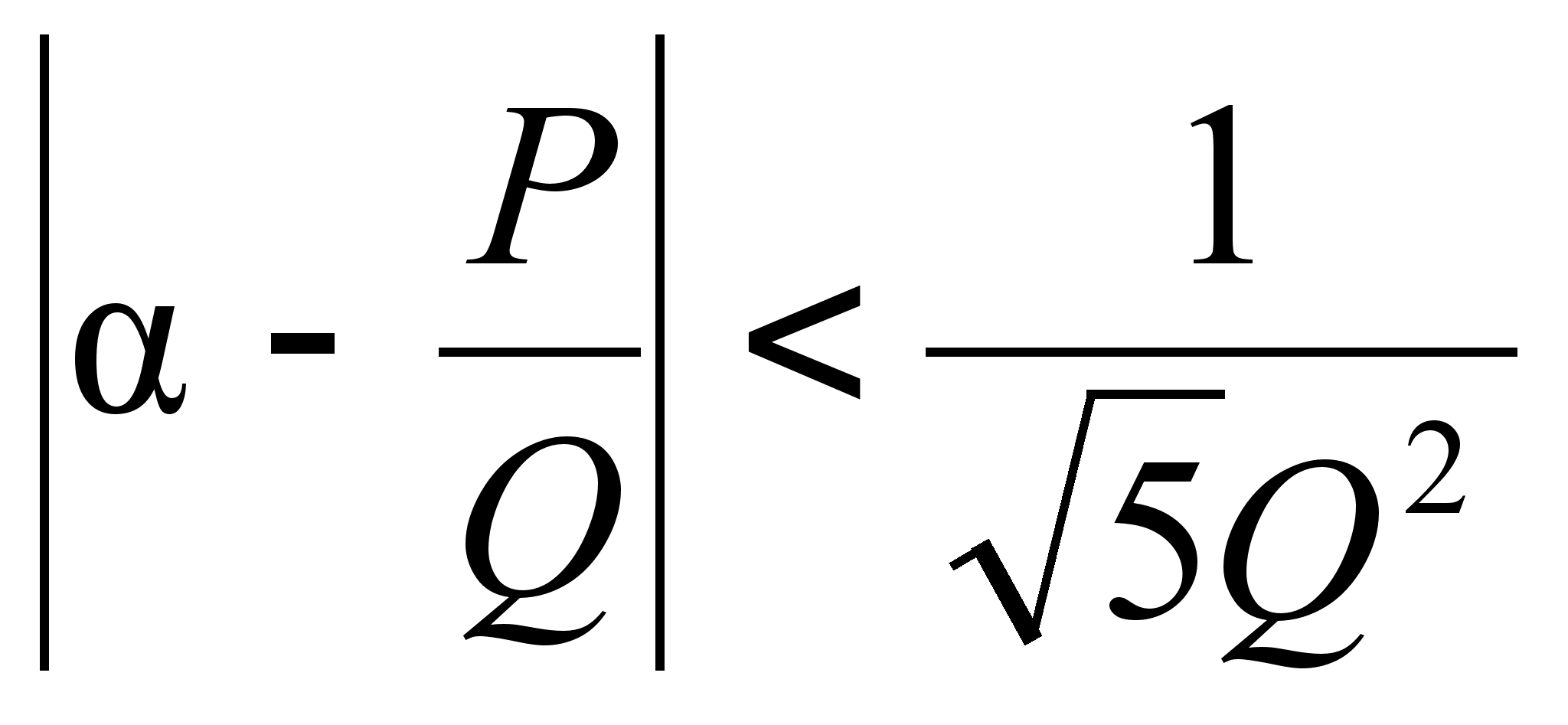 ,
был доказан
Борелем в 1903 году.
,
был доказан
Борелем в 1903 году.
Последним теоремам можно дать и другое очень важное истолкование.
Рассмотрим
для этого уравнение
![]() ,
где
,
где
![]() – любое действительное
иррациональное
число. Исключая
тривиальное
решение x=y=0,
это уравнение
не может иметь
решение в целых
числах. Однако
можно поставить
задачу о приближенном
его решении
в целых числах,
то есть о нахождении
таких пар чисел
x(x>0)
и y,
чтобы:
– любое действительное
иррациональное
число. Исключая
тривиальное
решение x=y=0,
это уравнение
не может иметь
решение в целых
числах. Однако
можно поставить
задачу о приближенном
его решении
в целых числах,
то есть о нахождении
таких пар чисел
x(x>0)
и y,
чтобы:
![]() или
или
![]() .
.
Теорема
Гурвица-Бореля
показывает,
что для
![]() всегда существует
бесконечное
множество таких
пар; если же
всегда существует
бесконечное
множество таких
пар; если же
![]() ,
то существуют
такие действительные
числа, для которых
таких пар имеется
лишь конечное
множество.
,
то существуют
такие действительные
числа, для которых
таких пар имеется
лишь конечное
множество.
Новая точка зрения получает в содружестве с методом Дирихле весьма значительное применение в теории диофантовых приближений.
§ 3. Квадратические иррациональности и периодические цепные дроби.
Рациональные
числа представляют
собой корни
уравнений
первой степени
вида
![]() с целыми коэффициентами.
с целыми коэффициентами.
Во множестве иррациональных чисел наиболее простыми являются те иррациональности, которые являются корнями квадратных уравнений с целыми коэффициентами; такие числа будем называть квадратическими иррациональностями.
Число
![]() называется
квадратической
иррациональностью,
если
называется
квадратической
иррациональностью,
если
![]() – иррациональный
корень некоторого
уравнения
– иррациональный
корень некоторого
уравнения
![]() (1) с
целыми коэффициентами,
не равными
одновременно
нулю.
(1) с
целыми коэффициентами,
не равными
одновременно
нулю.
При таком
![]() ,
очевидно, будет
a
,
очевидно, будет
a![]() 0,
c
0,
c![]() 0.
Коэффициенты
a,
b,
c
уравнения (1),
очевидно, можно
взять взаимно
простыми; в
этом случае
дискриминант
этого уравнения
0.
Коэффициенты
a,
b,
c
уравнения (1),
очевидно, можно
взять взаимно
простыми; в
этом случае
дискриминант
этого уравнения
![]() будем называть
также дискриминантом
будем называть
также дискриминантом
![]() .
Корни уравнения
(1) равны
.
Корни уравнения
(1) равны
![]() и
и
![]() ,
так что любую
квадратическую
иррациональность
,
так что любую
квадратическую
иррациональность
![]() можно представить
в виде
можно представить
в виде
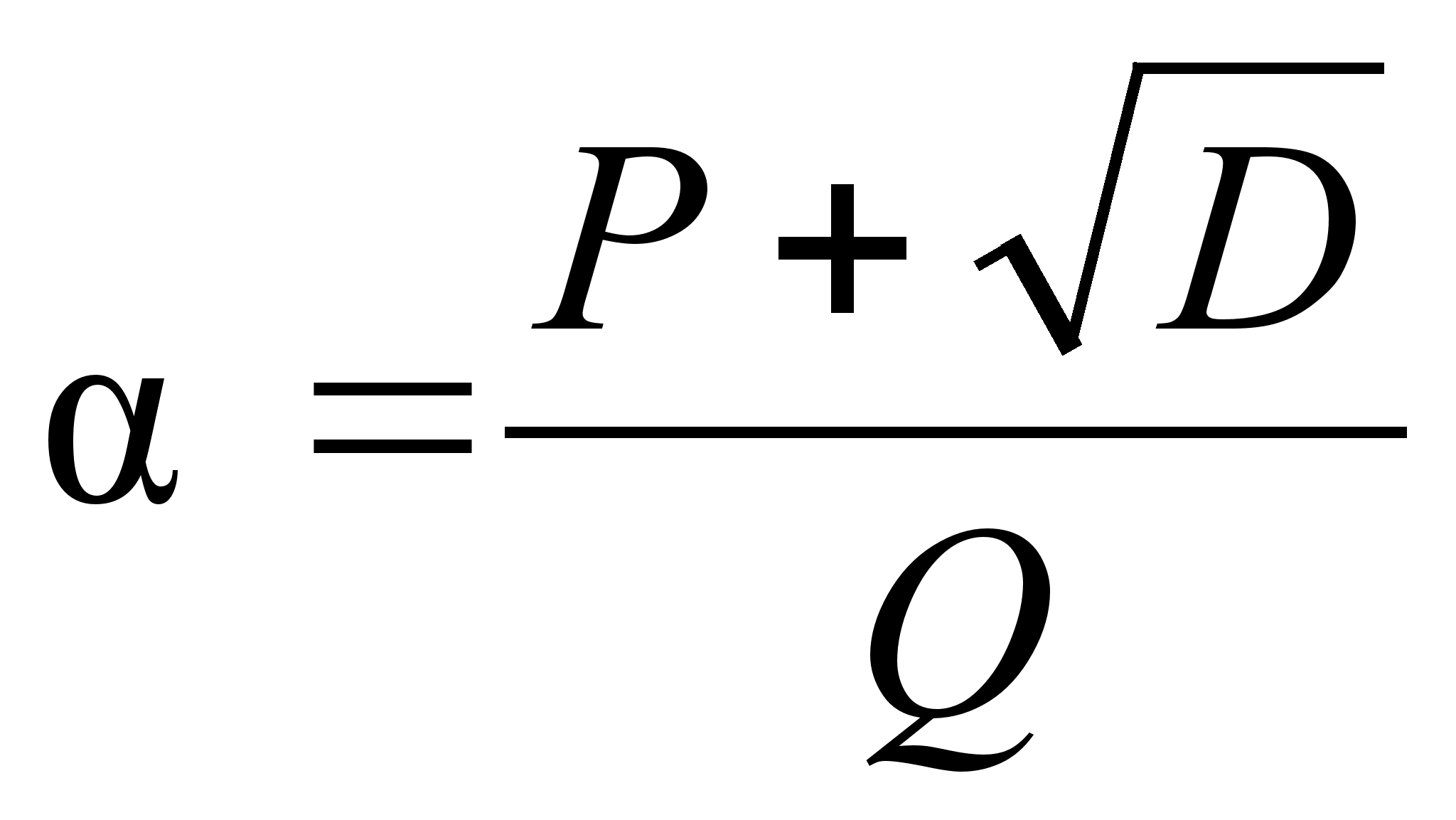 ,
где
P,
Q
– целые, а
D
(D>1)
– целое неквадратное
число.
,
где
P,
Q
– целые, а
D
(D>1)
– целое неквадратное
число.
Второй
корень уравнения
(1)
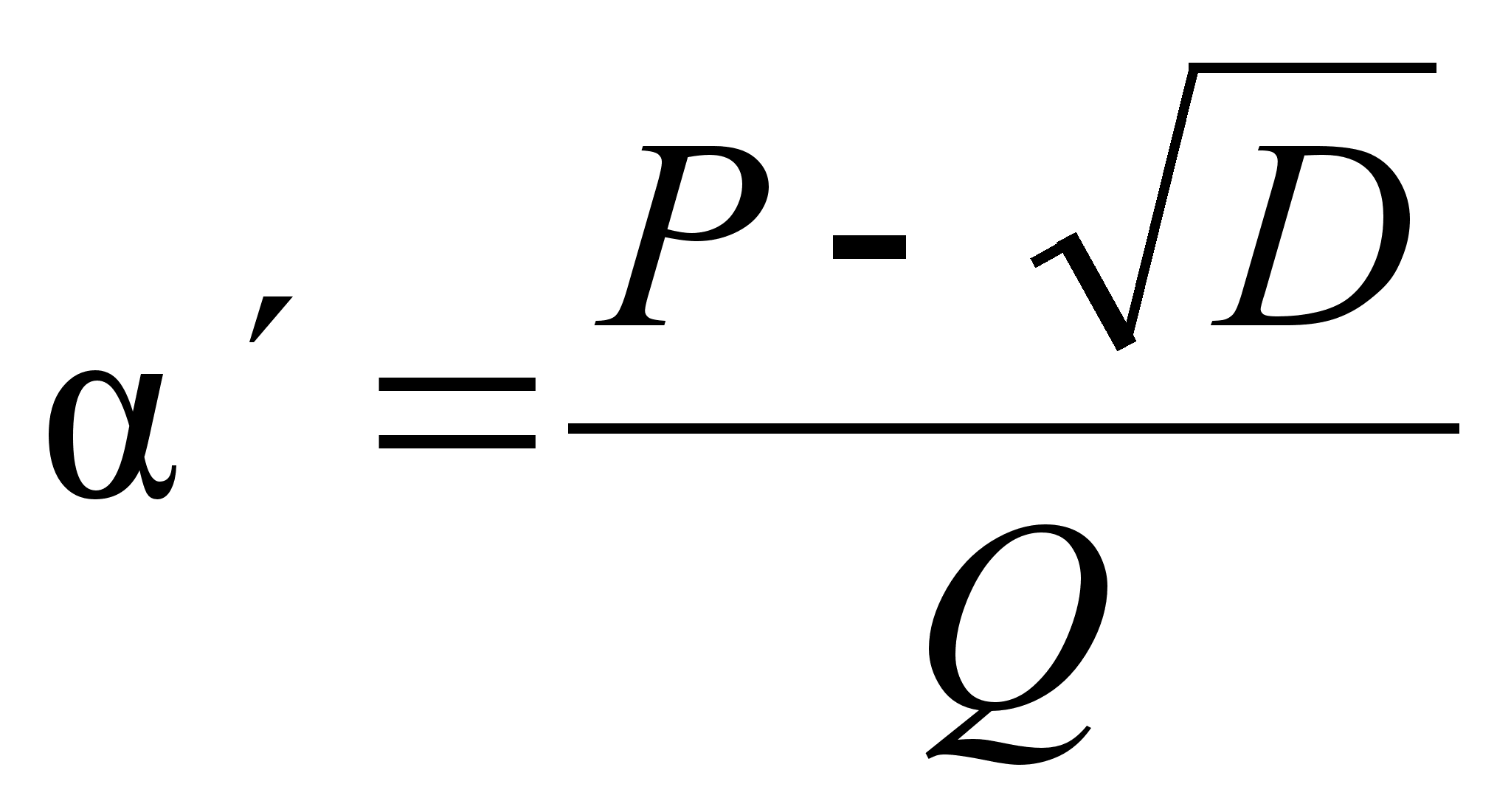 будем называть
иррациональностью,
сопряженной
с
будем называть
иррациональностью,
сопряженной
с
![]() .
.
В определении
квадратической
иррациональности
особенно важно
обратить внимание
на то, что речь
идет о квадратных
уравнениях
с целыми коэффициентами.
Любое
![]() является корнем
квадратного
уравнения и
даже уравнения
первой степени,
например уравнений
является корнем
квадратного
уравнения и
даже уравнения
первой степени,
например уравнений
![]() ,
x-
,
x-![]() =0.
=0.
Примеры:
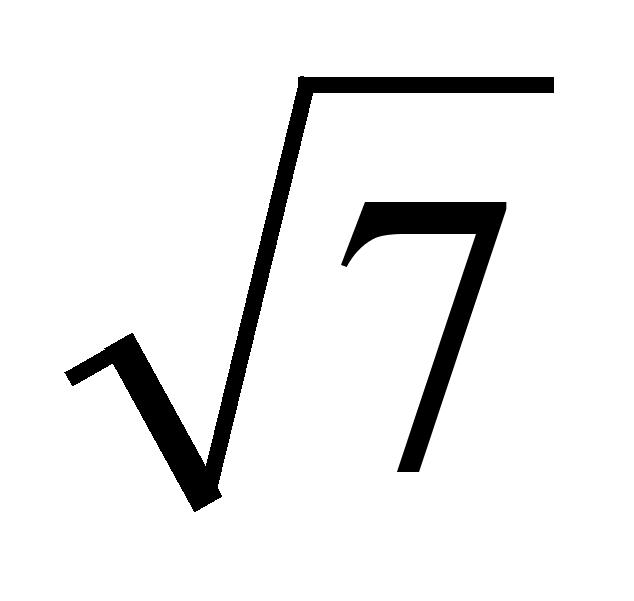 – квадратическая
иррациональность,
так как
– квадратическая
иррациональность,
так как
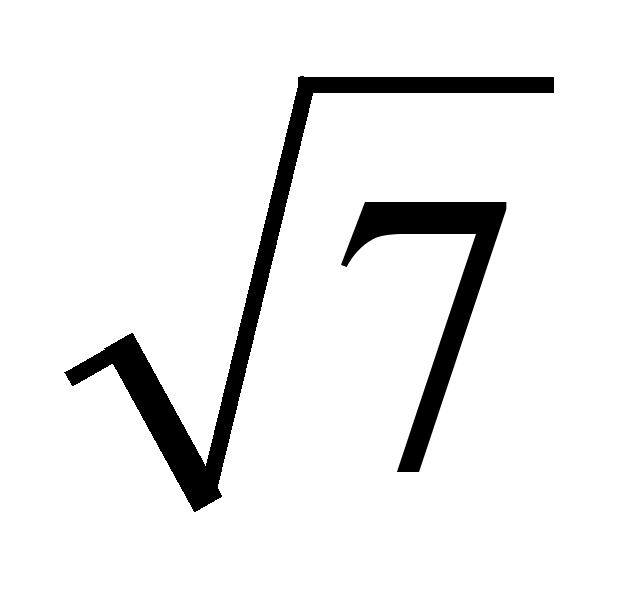 является
иррациональным
корнем уравнения
является
иррациональным
корнем уравнения
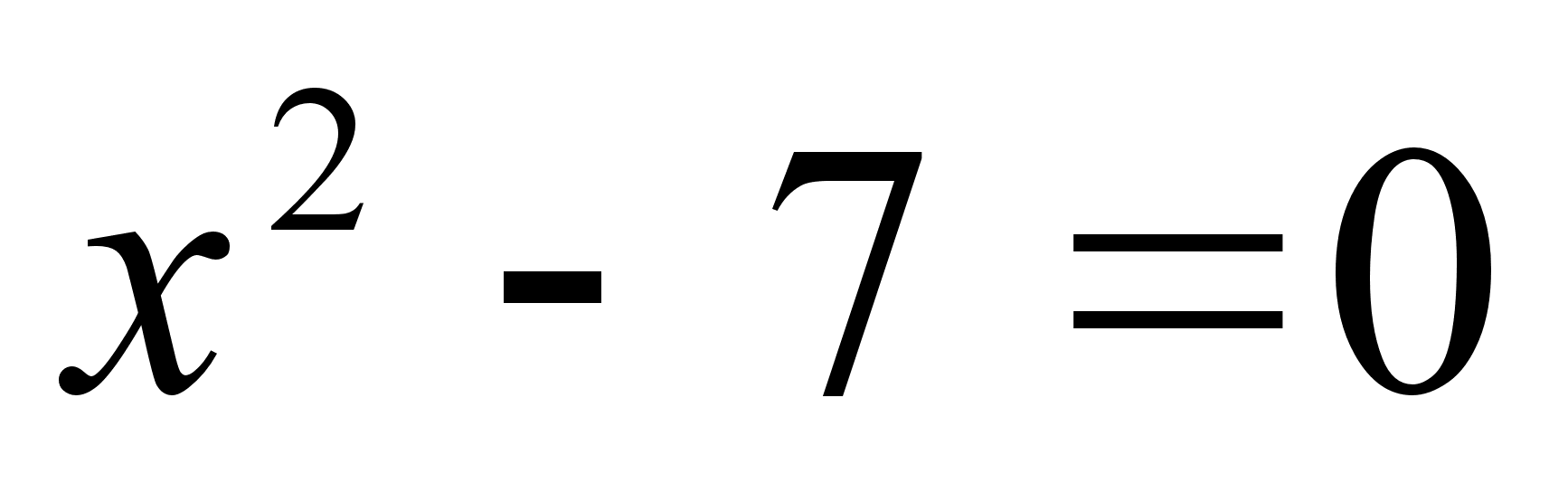 .
.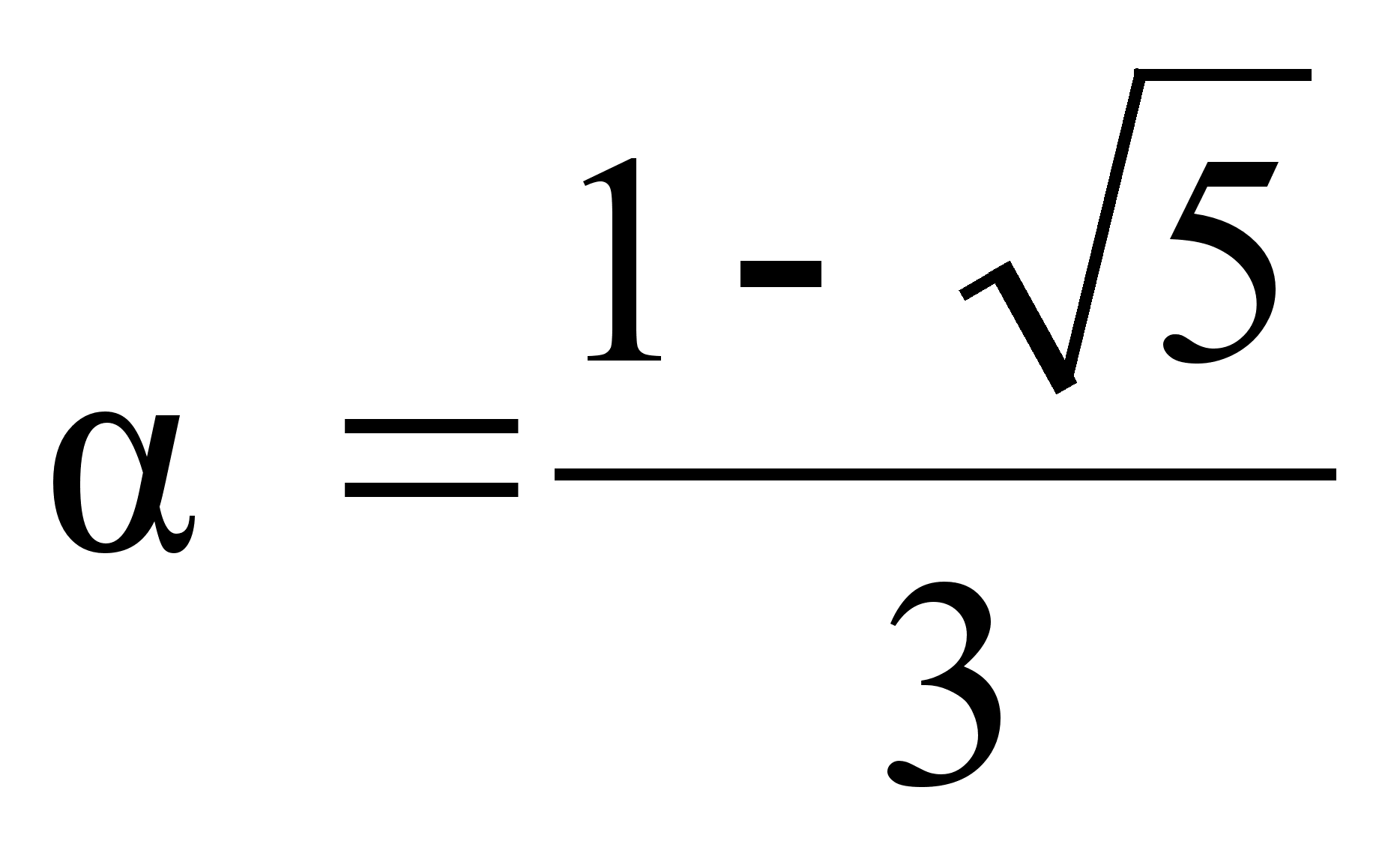 – квадратическая
иррациональность,
так как
– квадратическая
иррациональность,
так как
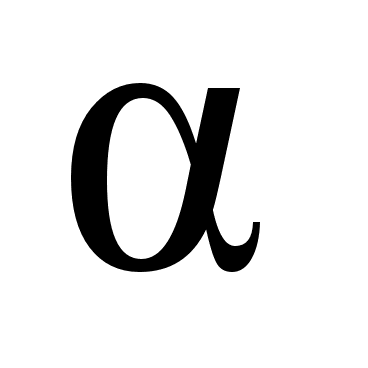 представляет
собой иррациональный
корень уравнения
представляет
собой иррациональный
корень уравнения
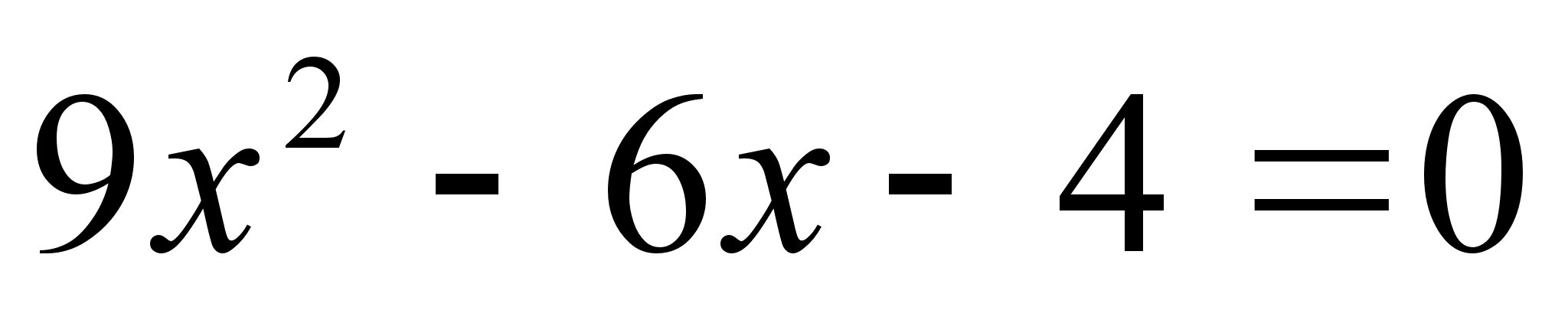 .
Здесь P=–1,
Q=–3,
D=5.
.
Здесь P=–1,
Q=–3,
D=5.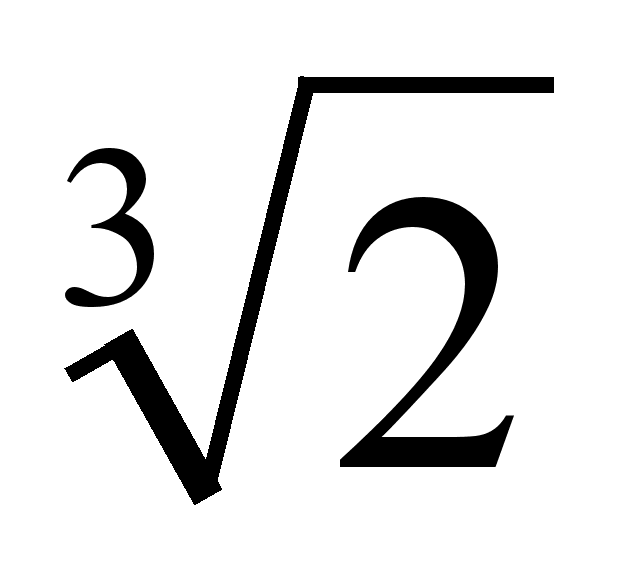 не является
квадратической
иррациональностью.
не является
квадратической
иррациональностью.
Действительно,
корень любого
квадратного
уравнения с
целыми коэффициентами
имеет вид
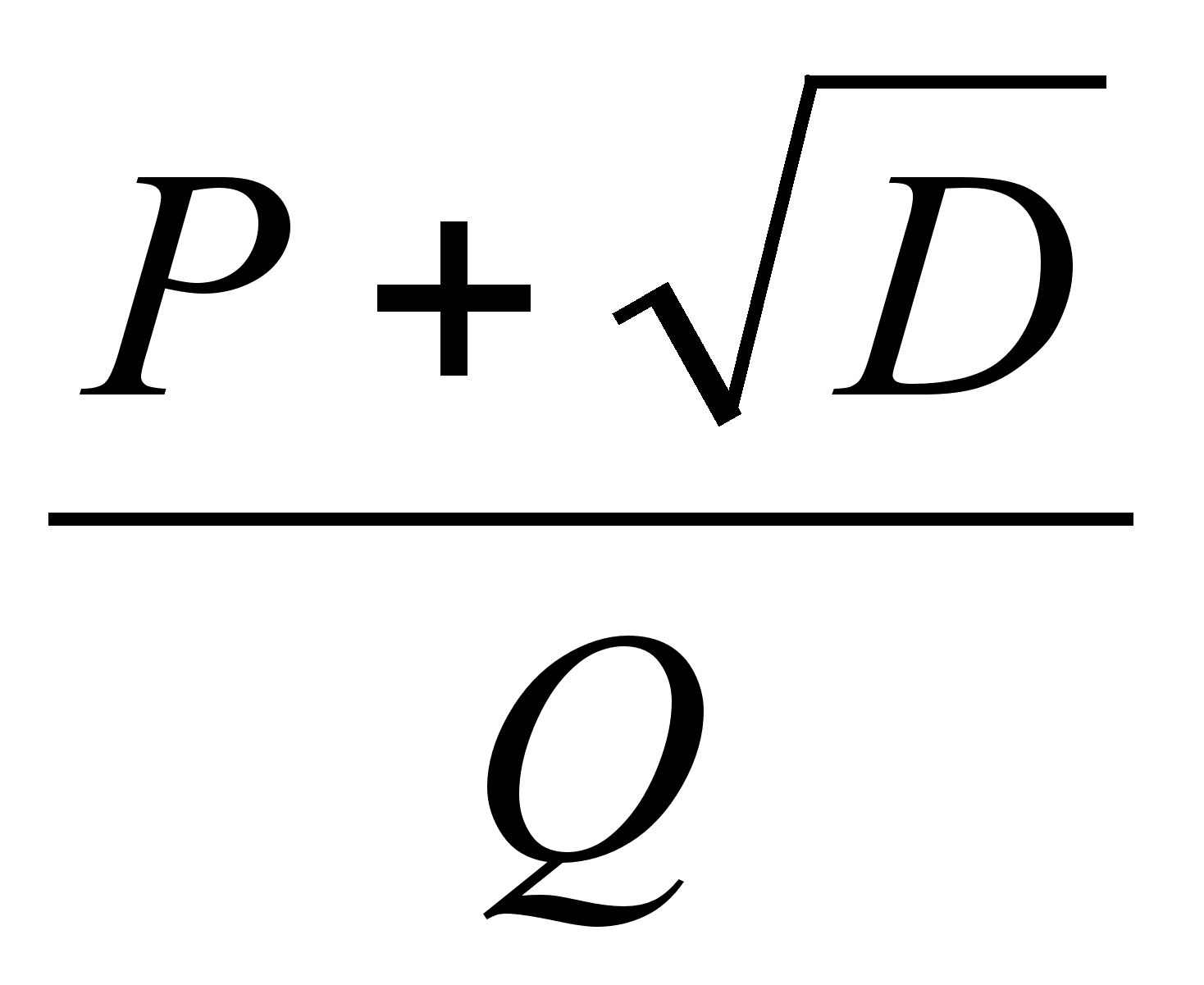 ,
где P,
Q,
D
,
где P,
Q,
D![]() ,
причем D>1.
Если бы мы имели
,
причем D>1.
Если бы мы имели
![]() =
=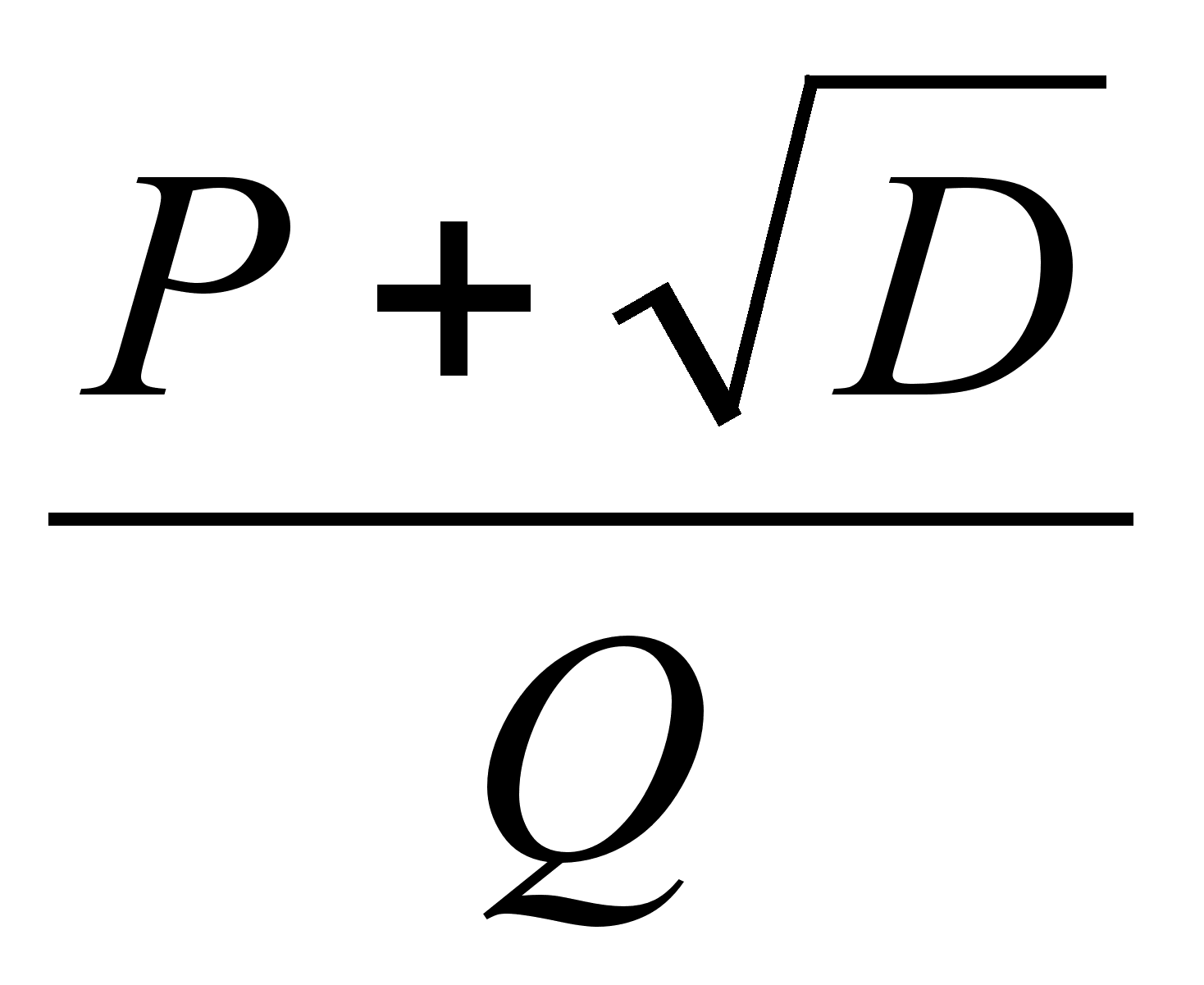 ,
то, возводя это
равенство в
куб, мы получили
бы, что
,
то, возводя это
равенство в
куб, мы получили
бы, что
![]() – рациональное
число, а следовательно,
рациональным
являлся бы и
– рациональное
число, а следовательно,
рациональным
являлся бы и
![]() ,
а это не так.
,
а это не так.
Теорема: Всякая периодическая непрерывная дробь изображает квадратическую иррациональность.
Доказательство:
Пусть
![]() –
смешанная
периодическая
цепная дробь,
то есть
–
смешанная
периодическая
цепная дробь,
то есть
![]() ,
где
,
где
![]() – чисто периодическая
цепная дробь.
– чисто периодическая
цепная дробь.
Обозначим
подходящие
дроби к
![]() и
и
![]() соответственно
через
соответственно
через
![]() и
и
![]() .
.
Так
как
![]() ,
то,
согласно формуле
(5) из 1.1 этой главы,
,
то,
согласно формуле
(5) из 1.1 этой главы,
![]() .
Выполнив необходимые
преобразования,
получаем:
.
Выполнив необходимые
преобразования,
получаем:
![]() .
.
Из
этой формулы
видно, что
![]() удовлетворяет
квадратному
уравнению с
целыми коэффициентами.
Кроме того,
удовлетворяет
квадратному
уравнению с
целыми коэффициентами.
Кроме того,
![]() - число иррациональное,
так как оно
представляет
бесконечную
непрерывную
дробь. Таким
образом,
- число иррациональное,
так как оно
представляет
бесконечную
непрерывную
дробь. Таким
образом,
![]() - квадратическая
иррациональность.
Но по той же
формуле
- квадратическая
иррациональность.
Но по той же
формуле
![]() ,
поэтому и
,
поэтому и
![]() является, очевидно,
квадратической
иррациональностью,
что и требовалось
доказать.
является, очевидно,
квадратической
иррациональностью,
что и требовалось
доказать.
Докажем обратную теорему, которая носит имя Лагранжа.
Теорема Лагранжа: Всякая действительная квадратическая иррациональность изображается периодической непрерывной дробью.
Доказательство:
Пусть
![]() – действительный
иррациональный
корень квадратного
уравнения
– действительный
иррациональный
корень квадратного
уравнения
![]() (1) с
целыми коэффициентами
a,
b,
c.
(1) с
целыми коэффициентами
a,
b,
c.
При
разложении
![]() в непрерывную
дробь получаем
в непрерывную
дробь получаем
![]() (2), где
(2), где
![]() – остаток
– остаток
![]() порядка k+1.
порядка k+1.
Подставляя
выражение
![]() из
(2) в
(1),
получаем
из
(2) в
(1),
получаем
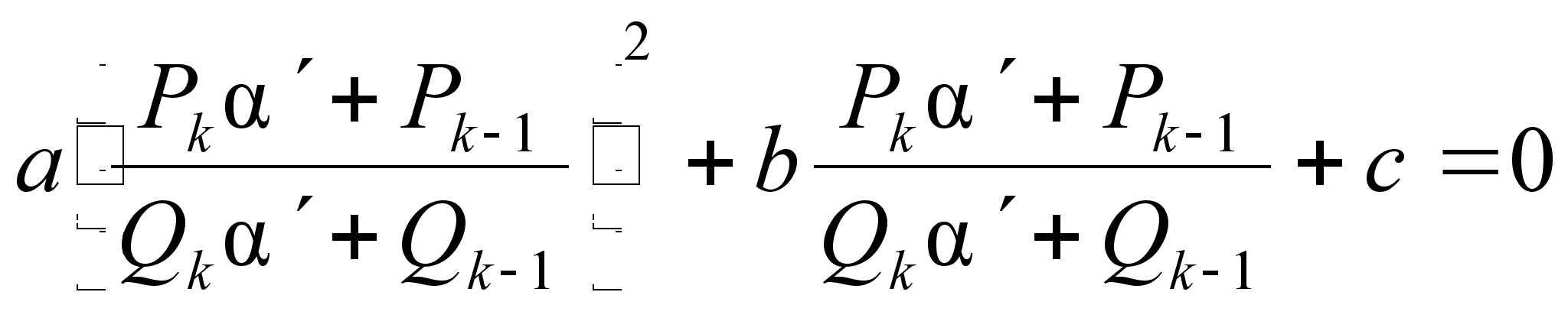
![]()
![]()
![]()
![]()
![]()
![]() (3),
где
(3),
где
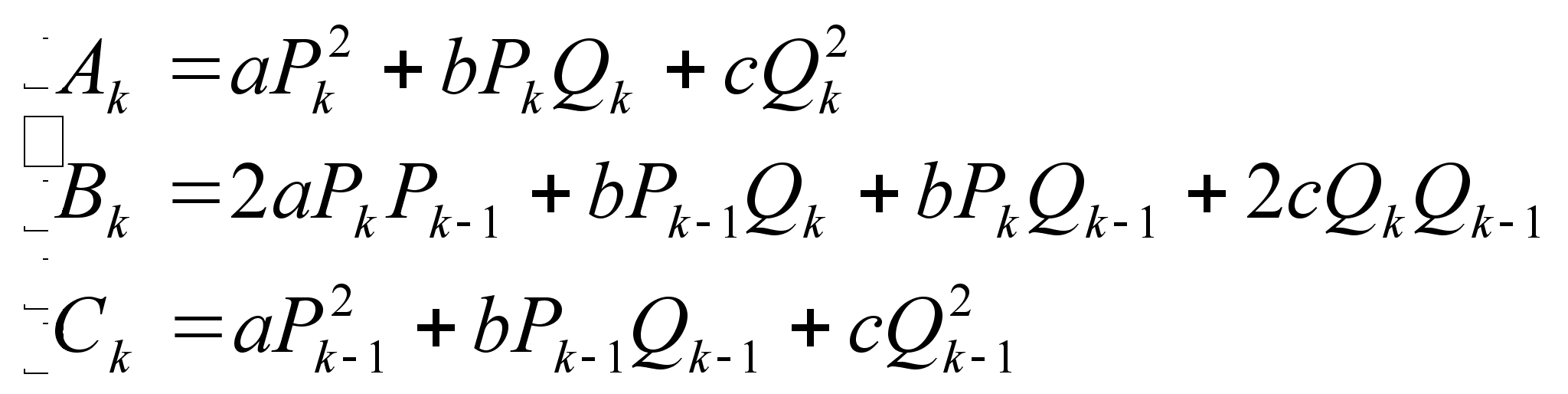 (4)
(4)
Отсюда,
во-первых, видно,
что
![]() (5), во-вторых,
можно непосредственным
вычислением
установить,
что
(5), во-вторых,
можно непосредственным
вычислением
установить,
что
![]() (6).
(6).
Таким образом, дискриминант уравнения (3) такой же, как и дискриминант уравнения (1), откуда следует, что он от k не зависит.
Идея
доказательства
в дальнейшем
заключается
в том, чтобы
показать, что
при данном
![]() коэффициенты
коэффициенты
![]() ,
,
![]() ,
,
![]() ограничены
по модулю.
ограничены
по модулю.
Если
этот факт на
самом деле имел
бы место, то
это означало
бы, что коэффициенты,
будучи целыми
числами, могут
принимать
только конечное
число различных
значений. Вместе
с тем и число
возможных
уравнений
(3) было
бы конечным,
хотя
k
пробегает
бесконечное
множество
значений. Но
в таком случае
и остатки
![]() (которые определяются
из (3)),
число которых
бесконечно,
могли бы принять
только конечное
число различных
значений. Поэтому
должны были
бы существовать
остатки
(которые определяются
из (3)),
число которых
бесконечно,
могли бы принять
только конечное
число различных
значений. Поэтому
должны были
бы существовать
остатки
![]() с одинаковыми
значениями,
а это уже означает,
что непрерывная
дробь – периодическая.
с одинаковыми
значениями,
а это уже означает,
что непрерывная
дробь – периодическая.
Итак,
докажем, что
![]() ,
,
![]() и
и
![]() ограничены
по абсолютной
величине. Достаточно
сделать это
для
ограничены
по абсолютной
величине. Достаточно
сделать это
для
![]() ,
так как в силу
соотношения
(5),
из ограниченности
,
так как в силу
соотношения
(5),
из ограниченности
![]() уже как следствие
вытекает
ограниченность
уже как следствие
вытекает
ограниченность
![]() ,
а в силу
(6) –
ограниченность
,
а в силу
(6) –
ограниченность
![]() .
.
Как
известно из
свойств подходящих
дробей,
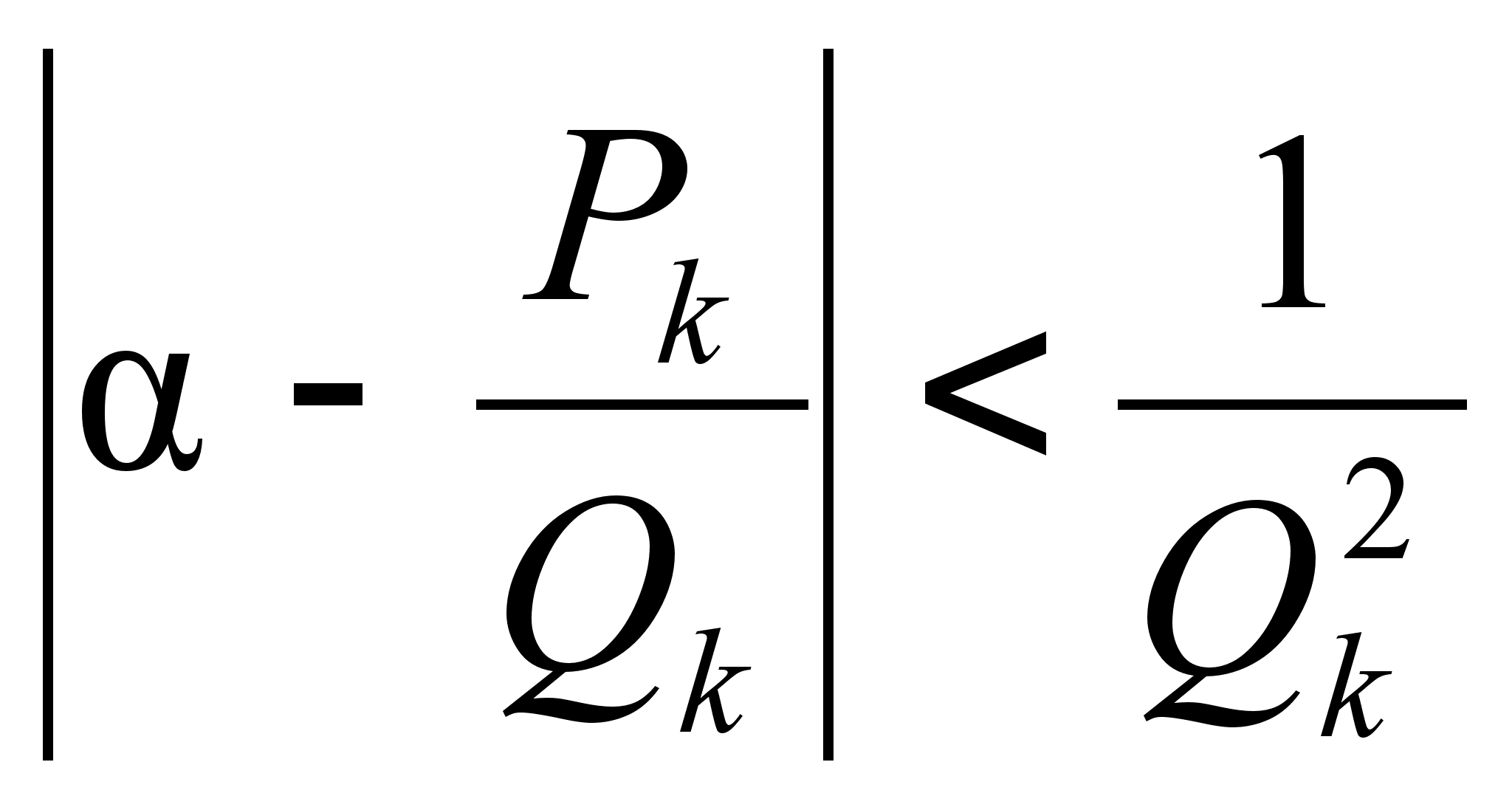 или
или
![]() ,
где
,
где
![]() ,
откуда
,
откуда
![]() .
.
Поэтому из первого равенства (4) имеем
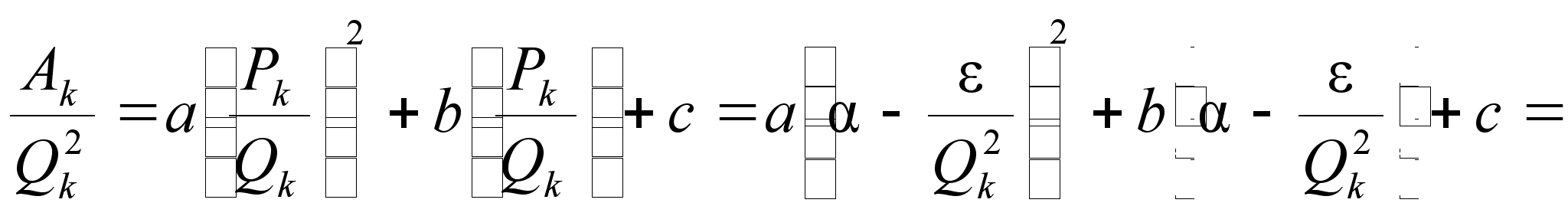
![]()
Так
как
![]() ,
то
,
то
![]()
![]() ,
,
то
есть
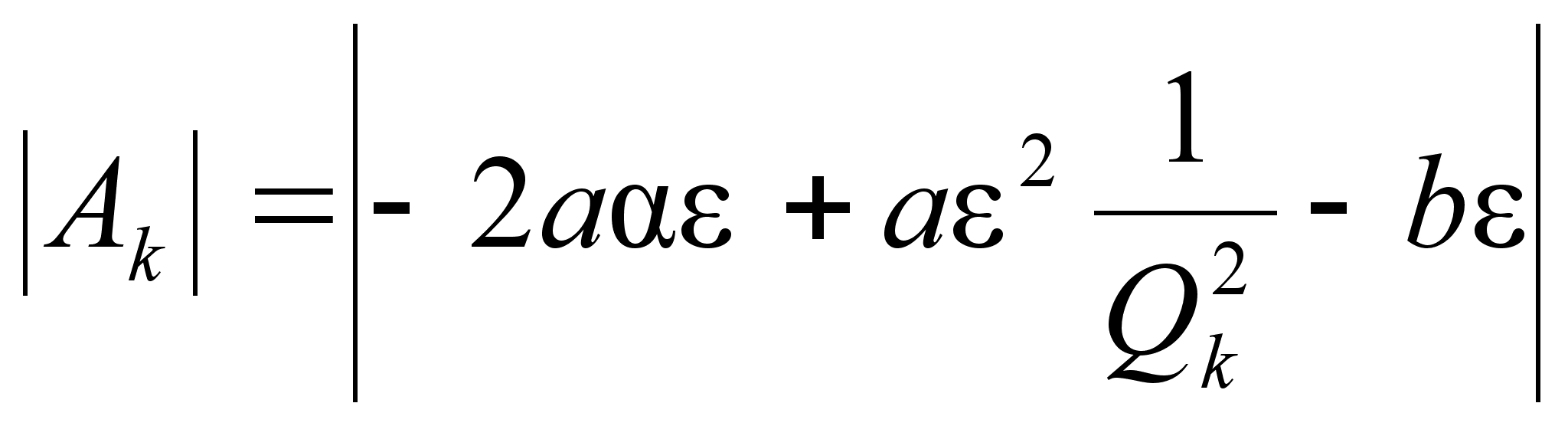 и
и
![]() ,
а это и доказывает
ограниченность
,
а это и доказывает
ограниченность
![]() .
.
Этим и завершается доказательство теоремы Лагранжа.
Отметим без доказательства следующие свойства разложений квадратических иррациональностей:
при разложении квадратного корня и целого положительного числа, не являющегося полным квадратом, период начинается со второго звена;
чисто периодическая цепная дробь получается тогда и только тогда, когда квадратическая иррациональность больше 1, а сопряженная иррациональность лежит в интервале (-1; 0) (это свойство было доказано Э. Галуа в 1828 году. Он доказал также, что в случае чисто периодического разложения сопряженная квадратическая иррациональность имеет те же элементы, но расположенные в обратном порядке).
Примеры:
Составить уравнение, один из корней которого разлагается в периодическую цепную дробь x и найти соответствующую иррациональность x=((2, 6, 1)).
Решение: x=(2, 6, 1, x).
Составляем схему вычисления числителей и знаменателей подходящих дробей.
|
2 |
6 |
1 |
x |
|
|
1 |
2 |
13 |
15 |
15x+13 |
|
0 |
1 |
6 |
7 |
7x+6 |
Итак,
![]() ,
откуда получаем:
,
откуда получаем:
![]()
![]() .
.
Положительное решение этого уравнения дает искомую периодическую дробь.
((2, 6,
1))=![]() - квадратическая
иррациональность.
Заметим, что
- квадратическая
иррациональность.
Заметим, что
![]() >1,
а
>1,
а
![]() – иррациональность,
сопряженная
с
x
– лежит в интервале
(-1;
0).
– иррациональность,
сопряженная
с
x
– лежит в интервале
(-1;
0).
Составить уравнение, один из корней которого разлагается в периодическую цепную дробь x=(3, (2, 1)) и найти соответствующую иррациональность.
Решение x=(3, y), где y=(2, 1, y). Составляем схему для вычисления числителей и знаменателей подходящих дробей y:
|
2 |
1 |
y |
|
|
1 |
2 |
3 |
3y+2 |
|
0 |
1 |
1 |
y+1 |
Следовательно,
![]() ,
,
![]()
![]()
![]() .
Так как y>0,
то мы должны
взять положительный
корень этого
уравнения
.
Так как y>0,
то мы должны
взять положительный
корень этого
уравнения
![]() .
Поэтому для
x
имеем
.
Поэтому для
x
имеем
![]()
![]() .
Таким образом,
искомая дробь
(3,
(2, 1))=
.
Таким образом,
искомая дробь
(3,
(2, 1))=![]() .
Для соответствующего
квадратного
уравнения имеем
.
Для соответствующего
квадратного
уравнения имеем
![]() ,
откуда получаем:
,
откуда получаем:
![]()
![]()
![]()
![]()
![]() .
.
§4. Представление действительных чисел цепными дробями общего вида.
Рассмотренные до сих пор правильные бесконечные и конечные цепные дроби являются частным случаем бесокнечных и конечных цепных дробей общего вида:
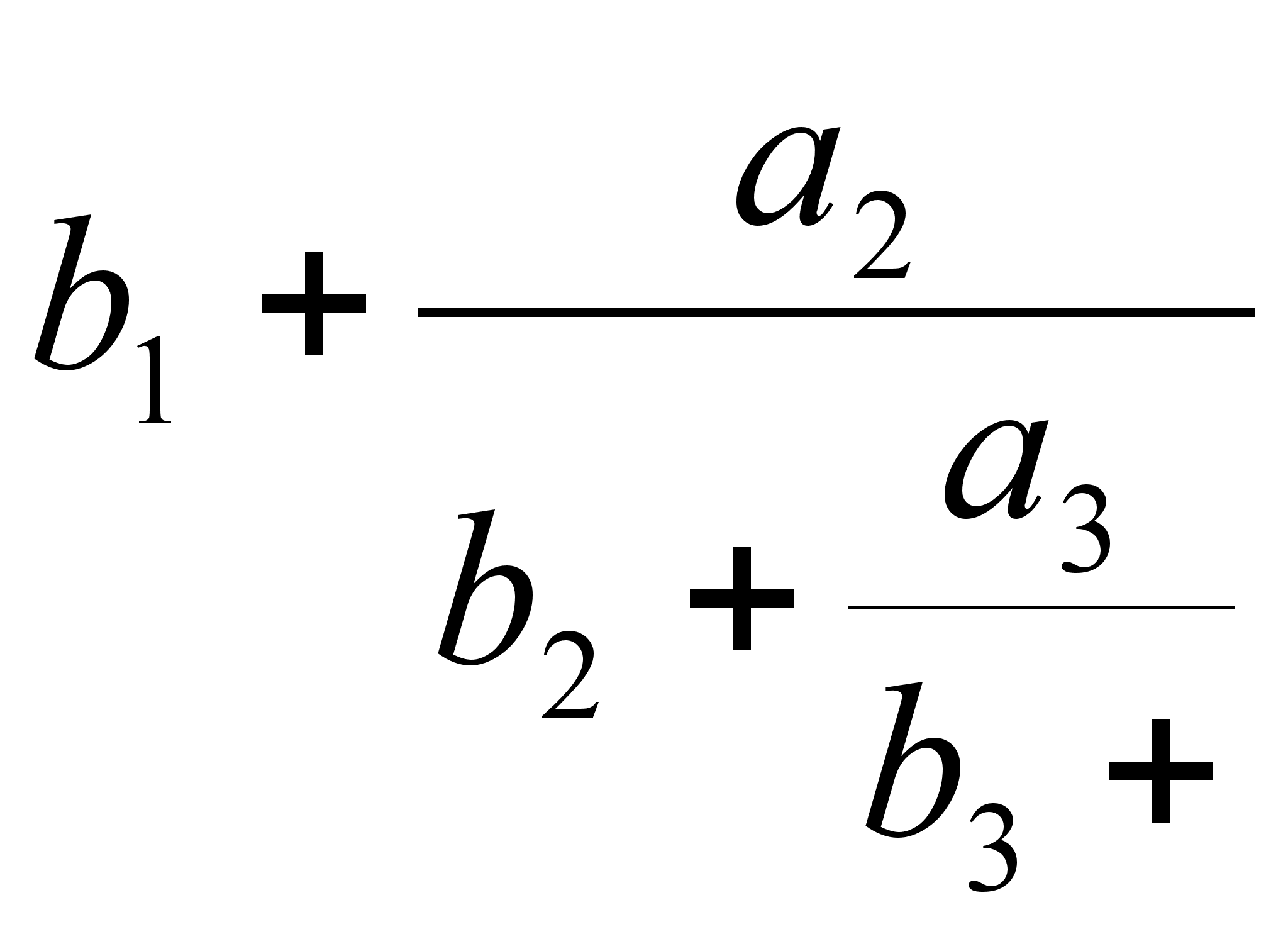 (1),
(1),
![]()
когда
в них принимается,
что все
![]() ,
,
![]() ,
а остальные
,
а остальные
![]() .
.
В общем
случае элементы
цепной дроби
![]() и
и
![]() ,
k>1
могут принимать
произвольные,
отличные от
0 рациональные
значения, а
,
k>1
могут принимать
произвольные,
отличные от
0 рациональные
значения, а
![]() может также
быть равно
нулю.
может также
быть равно
нулю.
При помощи
цепных дробей
общего вида
одно и то же
рациональное
число можно
представить
различными
способами.
Например,
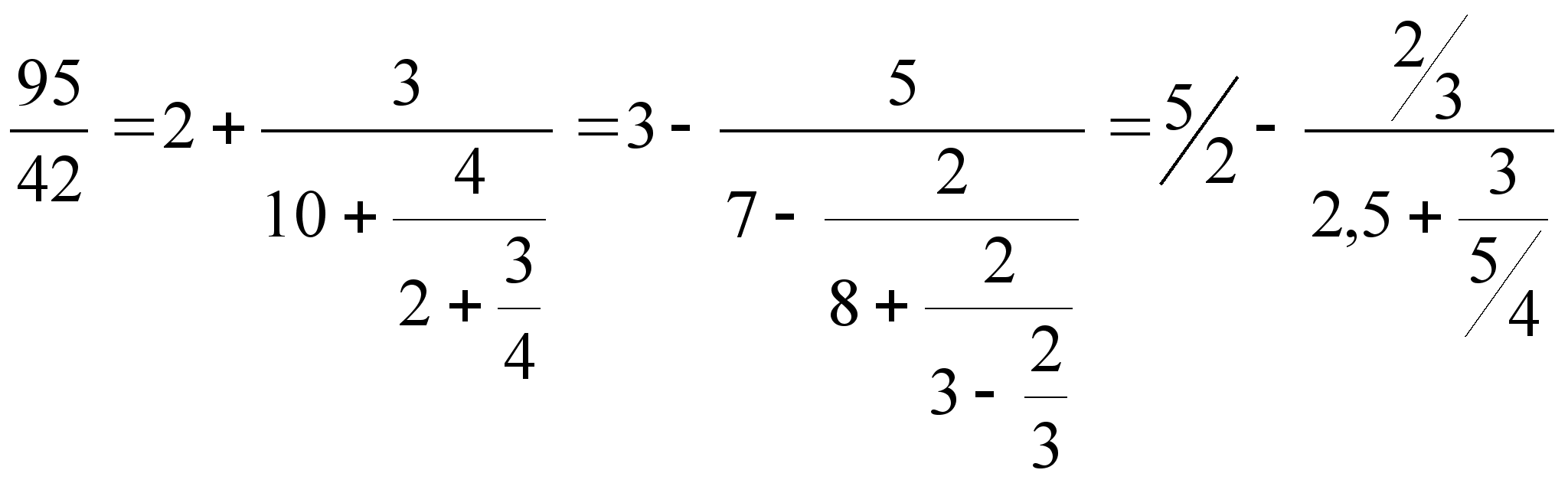 .
.
В цепной
дроби (1),
которую записывают
также иначе,
например,
![]() (
(![]() )
или
)
или
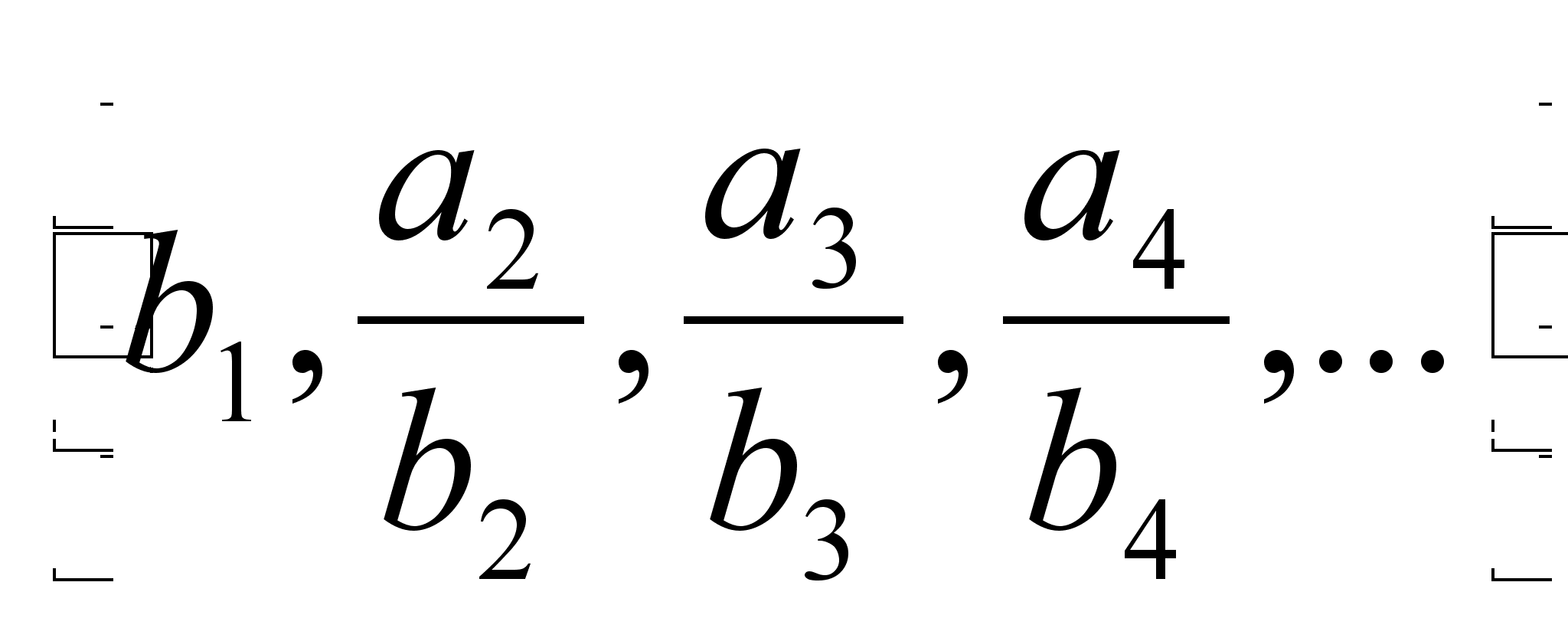 (
(![]() )
числа
)
числа
![]() и
и
![]() (k=2,
3, …)
называют звеньями,
(k=2,
3, …)
называют звеньями,
![]() и
и
![]() – членами
k–го
звена, из них
– членами
k–го
звена, из них
![]() – частным числителем,
а
– частным числителем,
а
![]() – частным
знаменателем.
– частным
знаменателем.
Чтобы
получить разложение
рационального
числа
![]() в конечную
цепную дробь
(1),
можно все
в конечную
цепную дробь
(1),
можно все
![]() и
и
![]() ,
за исключением
одного, выбрать
произвольно.
,
за исключением
одного, выбрать
произвольно.
Можно,
например, найти
разложение
![]() ;
для этого следует
положить
;
для этого следует
положить
![]() .
Можно цепную
дробь преобразовать
так, чтобы все
.
Можно цепную
дробь преобразовать
так, чтобы все
![]() были равны 1,
то есть, чтобы
(1) приняло
вид
были равны 1,
то есть, чтобы
(1) приняло
вид
![]() (2).
(2).
Так,
например,
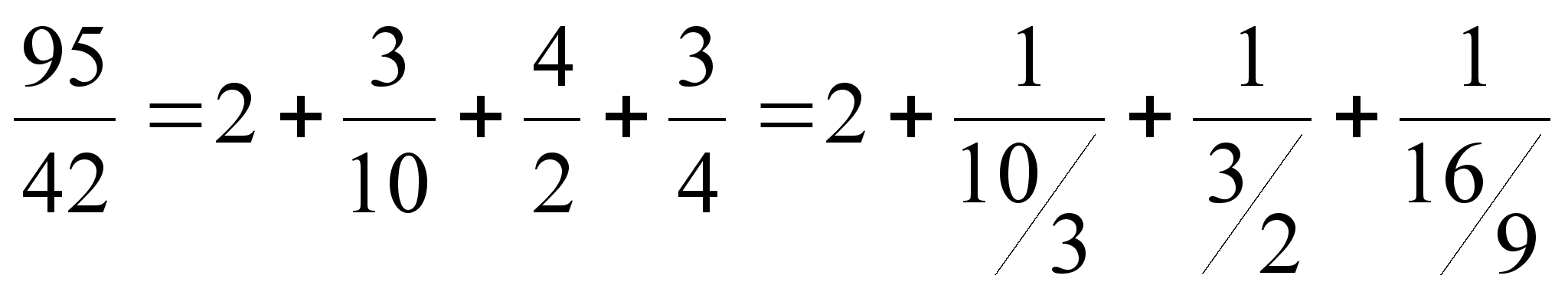 .
Дроби вида
(2) называют
обыкновенными
цепными дробями,
а
.
Дроби вида
(2) называют
обыкновенными
цепными дробями,
а
![]() ,
,
![]() ,
…,
,
…,
![]() – их неполными
частными. Правильные
цепные дроби
можно поэтому
определить
как обыкновенные
цепные дроби
с целыми положительными
неполными
частными, начиная
с
– их неполными
частными. Правильные
цепные дроби
можно поэтому
определить
как обыкновенные
цепные дроби
с целыми положительными
неполными
частными, начиная
с
![]() ,
причем
,
причем
![]() может быть
любым целым
числом.
может быть
любым целым
числом.
Правильные цепные дроби являются наиболее простыми и наиболее изученными среди цепных дробей общего вида, однако и другие цепные дроби играют большую роль и имеют важные применения, например, в приближенном анализе, где при их помощи без сложных выкладок получают дробно-рациональные приближения функций.
Рассмотрим обзорно некоторые свойства цепных дробей общего вида.
Происхождение таких цепных дробей связано с обобщенным алгоритмом Евклида.
Если
мы имеем систему
равенств
![]() ,
,
![]() ,
,
![]() ,
… с
произвольными
рациональными
числами, то при
b,
c,
d
,
… с
произвольными
рациональными
числами, то при
b,
c,
d![]() 0,
из них следуют
равенства
0,
из них следуют
равенства
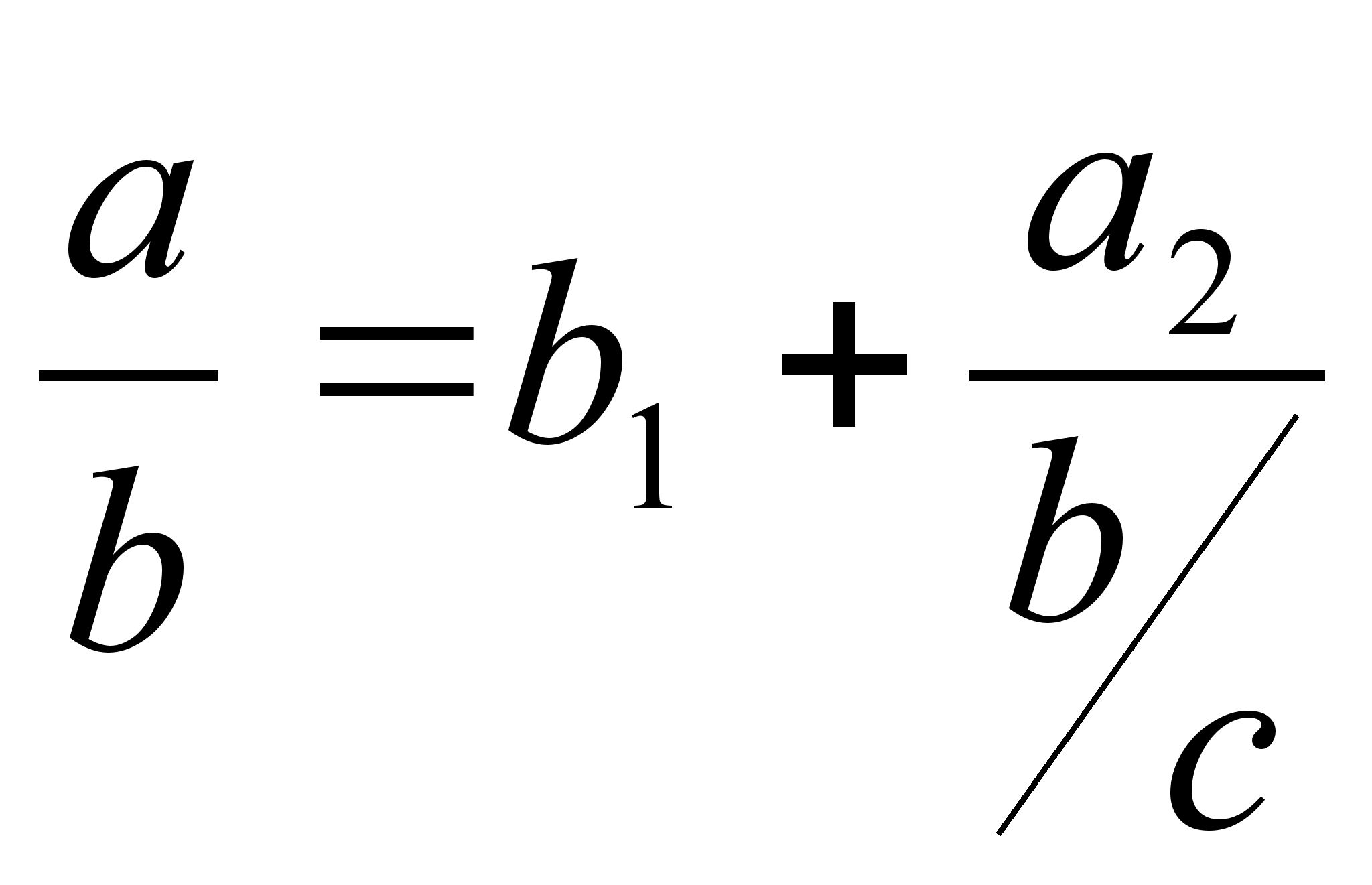 ,
,
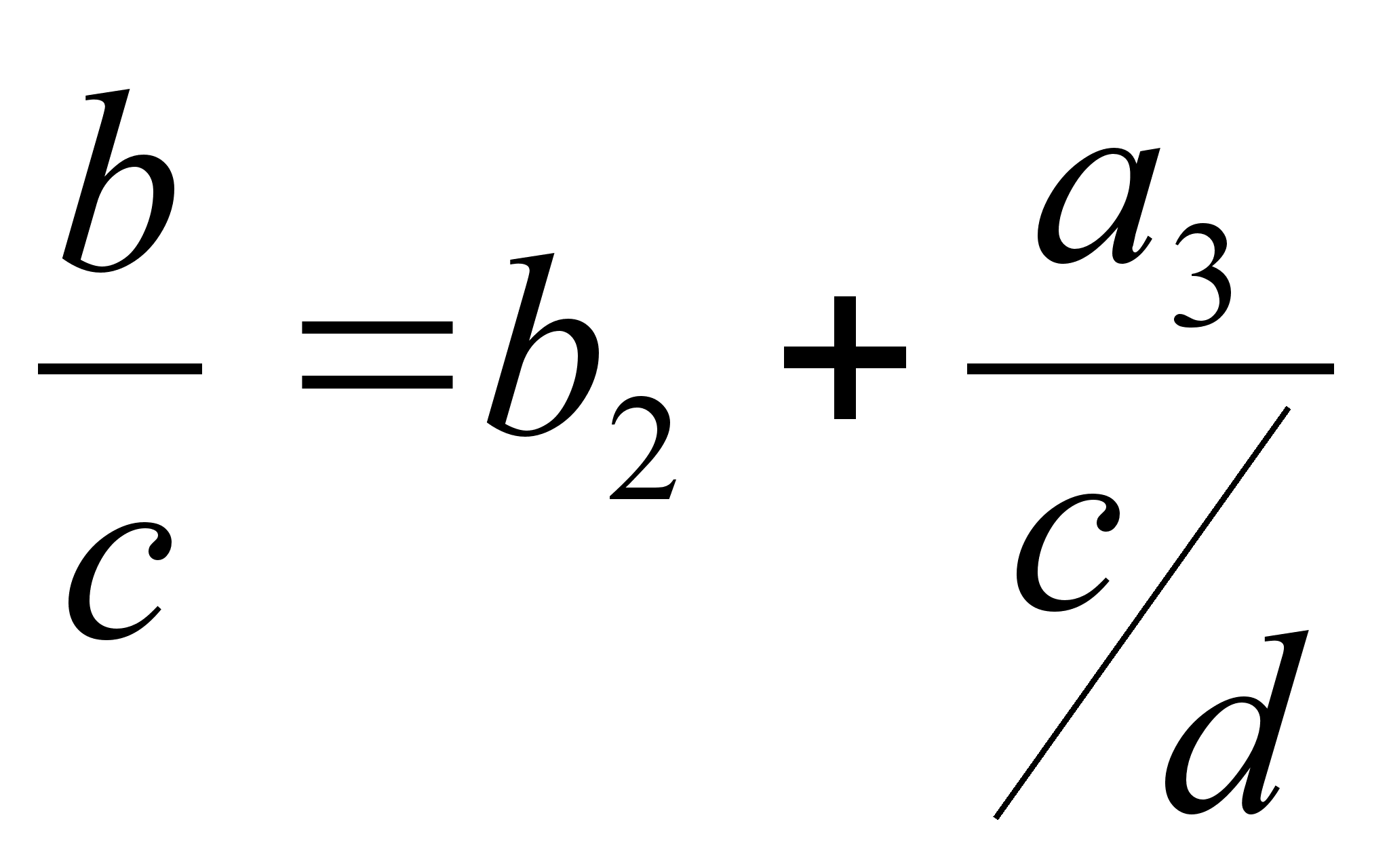 ,
,
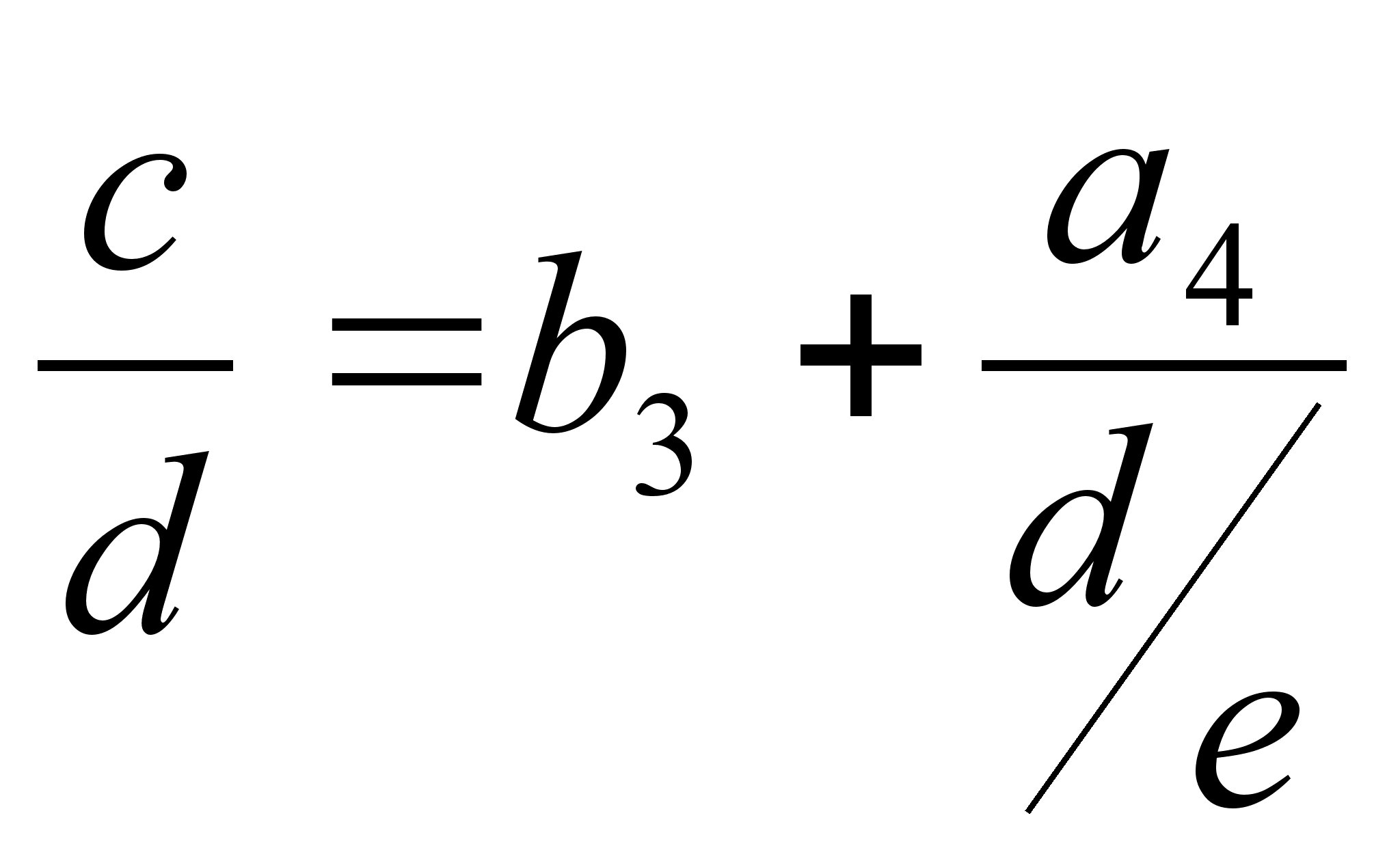 ,
…, так
что, подставляя
по цепочке,
получаем
,
…, так
что, подставляя
по цепочке,
получаем
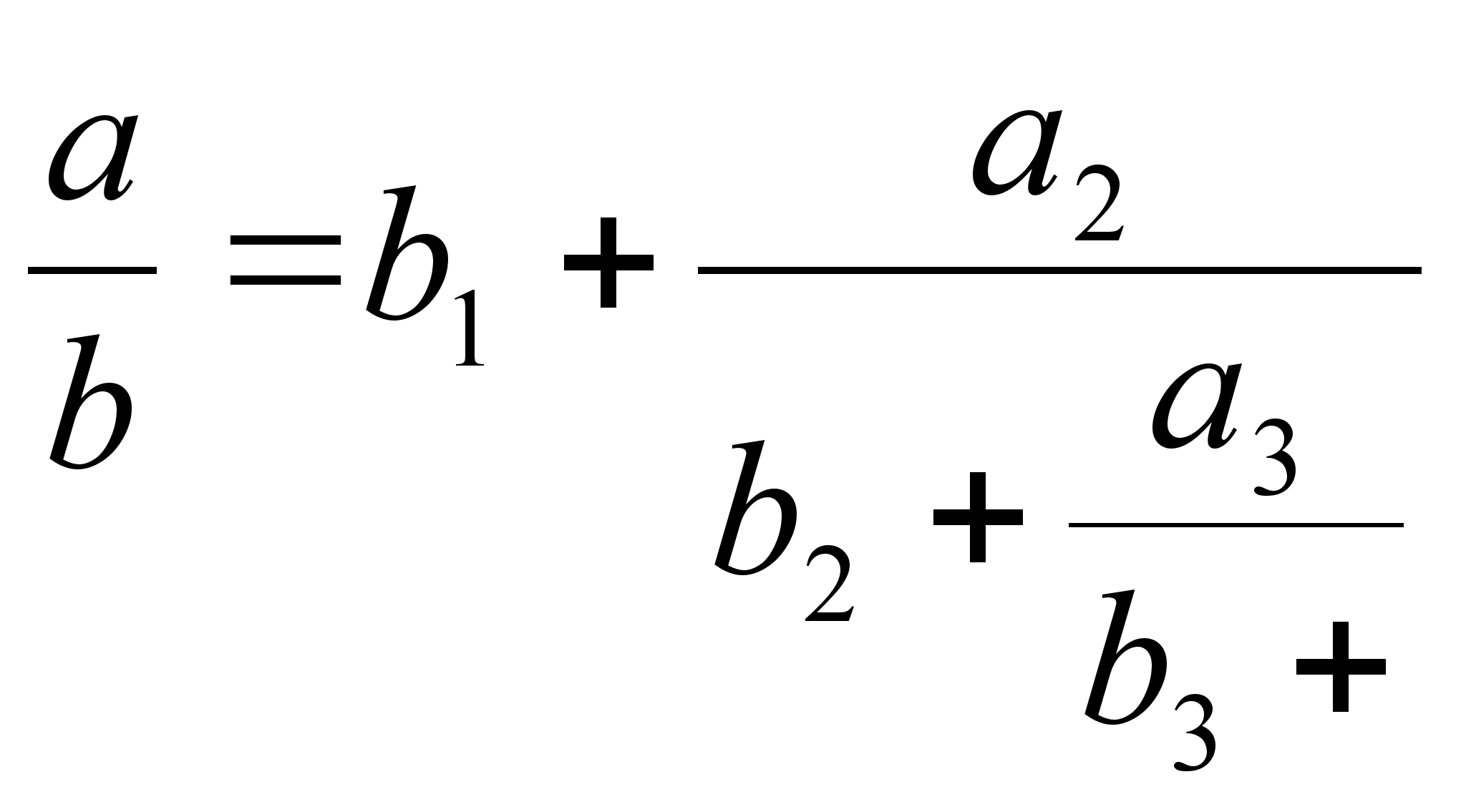 .
.
![]()
k-я
подходящая
дробь
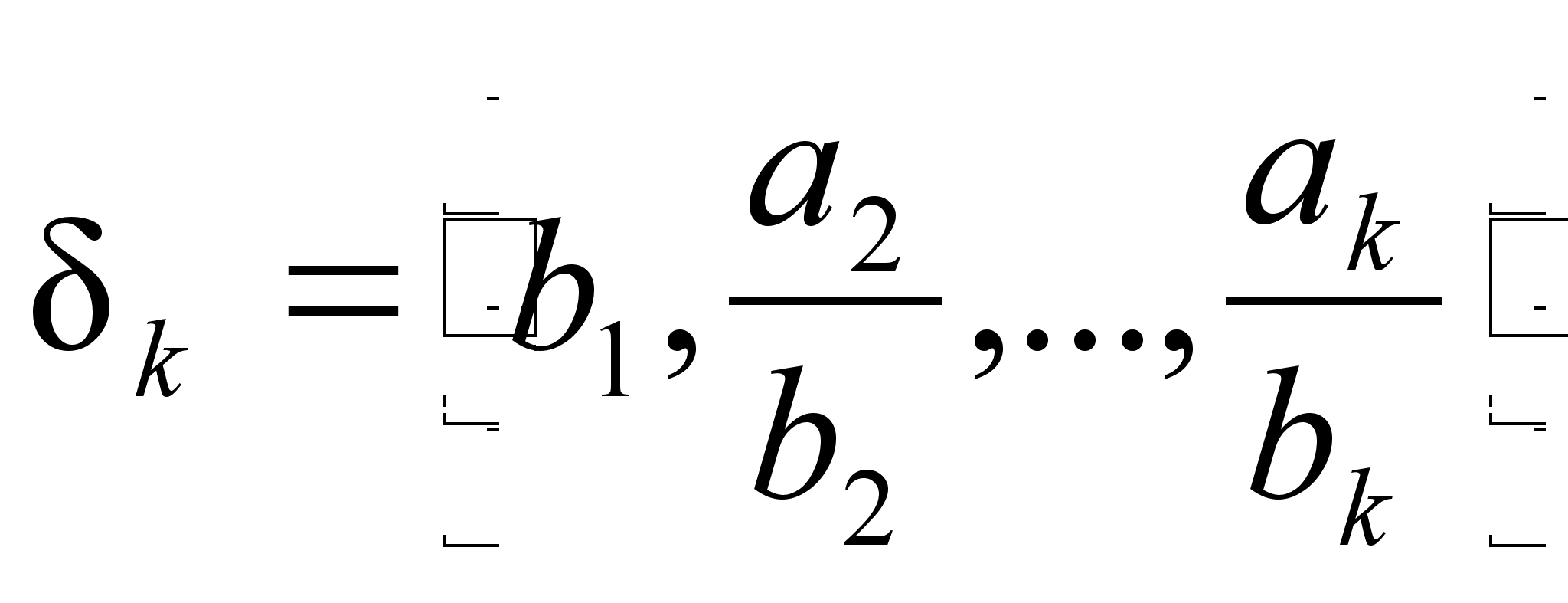 определяется
для
определяется
для
![]() по формуле
по формуле
![]() при условии,
что
при условии,
что
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Пользуясь
ею, найдем, например,
подходящие
дроби для разложения
![]() .
Имеем
.
Имеем
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Заметим, что
получаемые
в процессе
рекуррентного
вычисления
подходящие
дроби могут
быть сократимыми,
но сокращать
их можно лишь
при определенных
условиях.
.
Заметим, что
получаемые
в процессе
рекуррентного
вычисления
подходящие
дроби могут
быть сократимыми,
но сокращать
их можно лишь
при определенных
условиях.
Свойства подходящих дробей цепных дробей общего вида с положительными элементами и правильных цепных дробей вполне аналогичны.
Бесконечная
цепная дробь
(1) называется
сходящейся,
если существует
конечный предел
![]() ;
в таком случае
;
в таком случае
![]() принимается
за значение
этой дроби. Не
всегда общие
бесконечные
цепные дроби
являются сходящимися,
даже тогда,
когда они имеют
лишь положительные
элементы.
принимается
за значение
этой дроби. Не
всегда общие
бесконечные
цепные дроби
являются сходящимися,
даже тогда,
когда они имеют
лишь положительные
элементы.
Существует ряд признаков сходимости цепных дробей:
Пусть дана непрерывная дробь вида
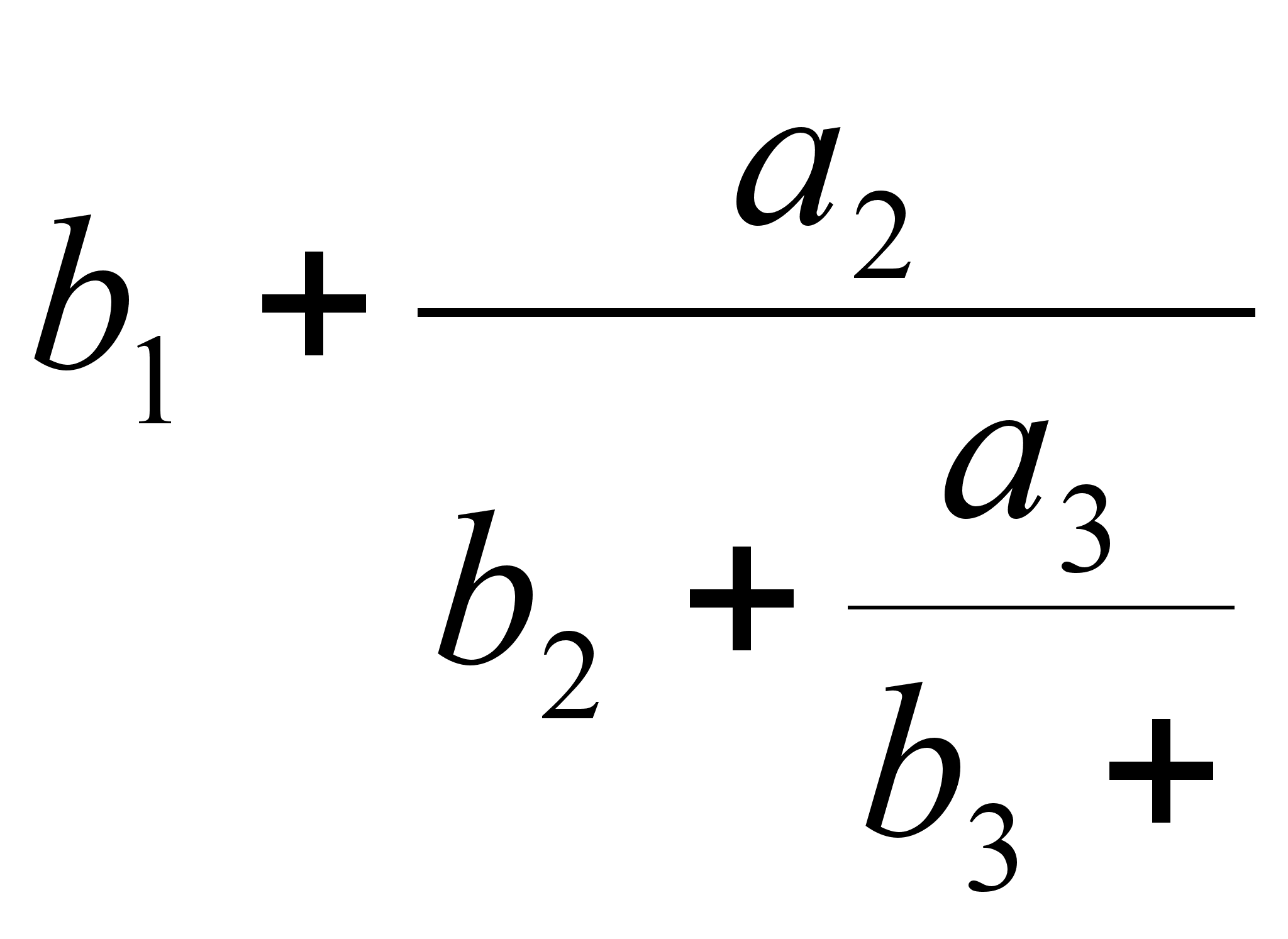 ,
где
,
где
![]() ,
,
![]()
![]()
Пусть
 ,
все члены
последовательностей
,
все члены
последовательностей
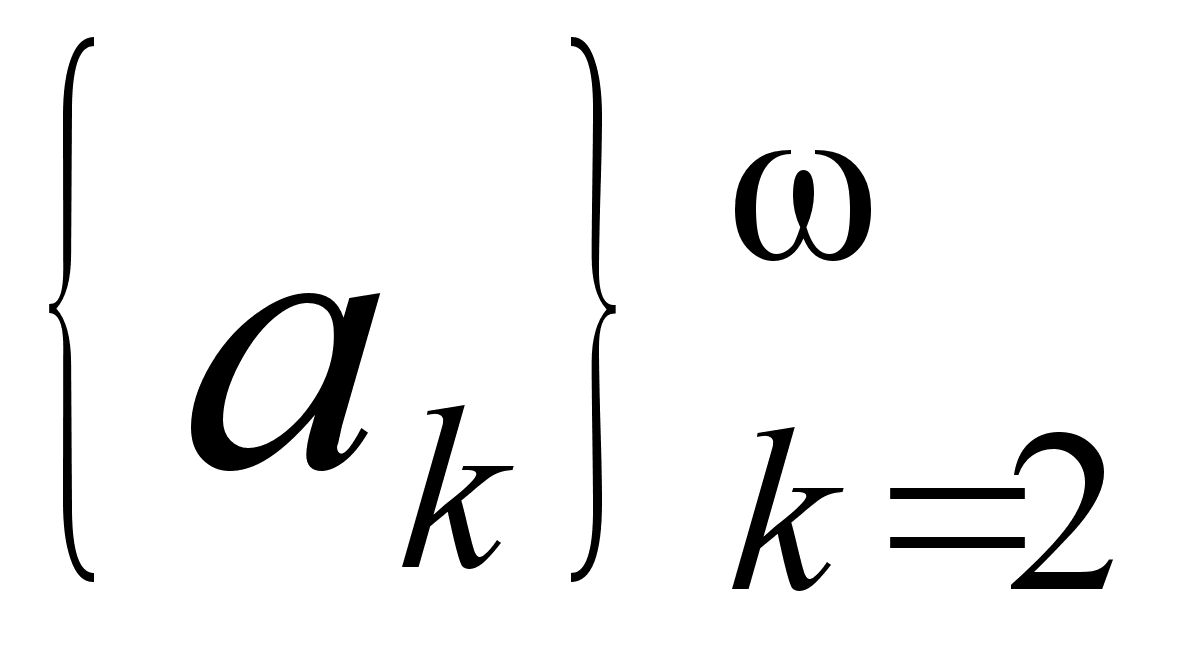 ,
,
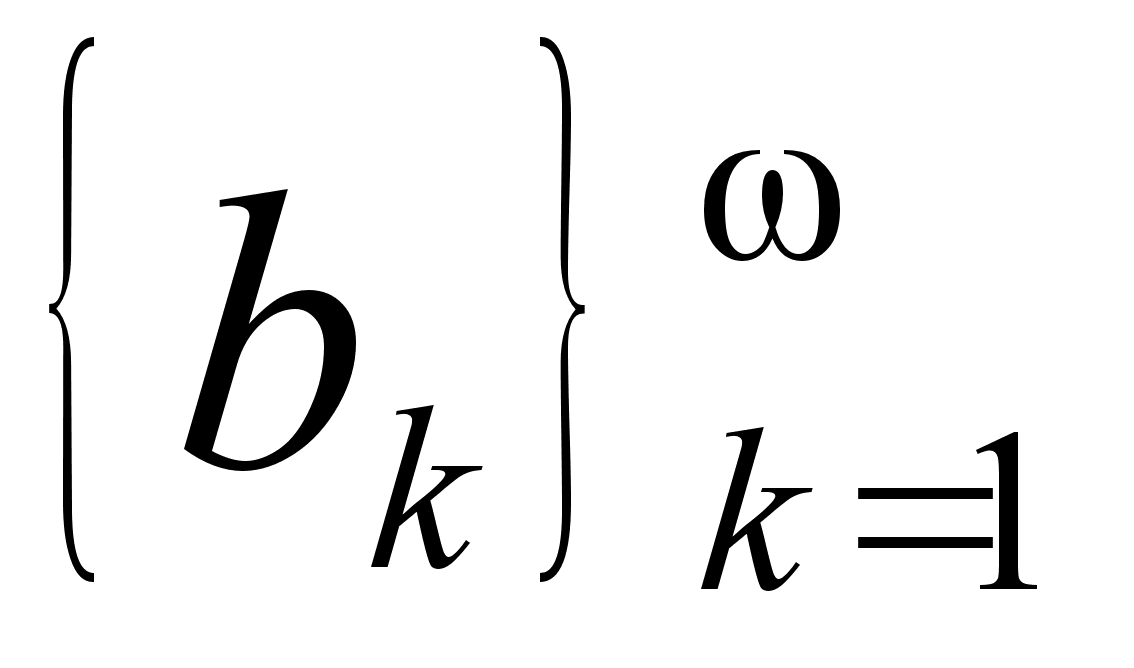 действительные
числа и
действительные
числа и
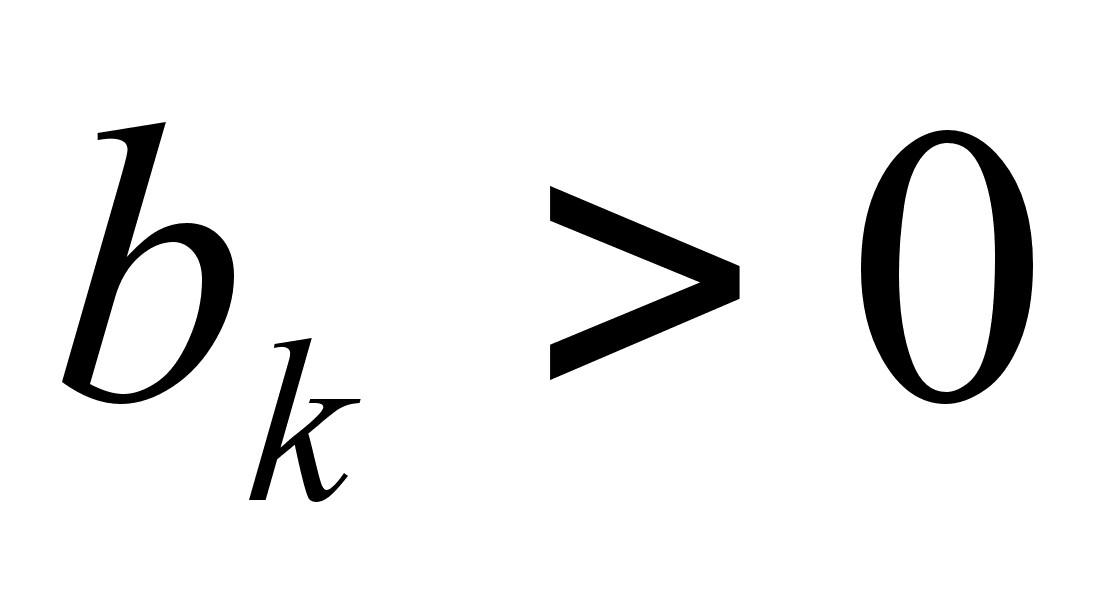 для всех
для всех
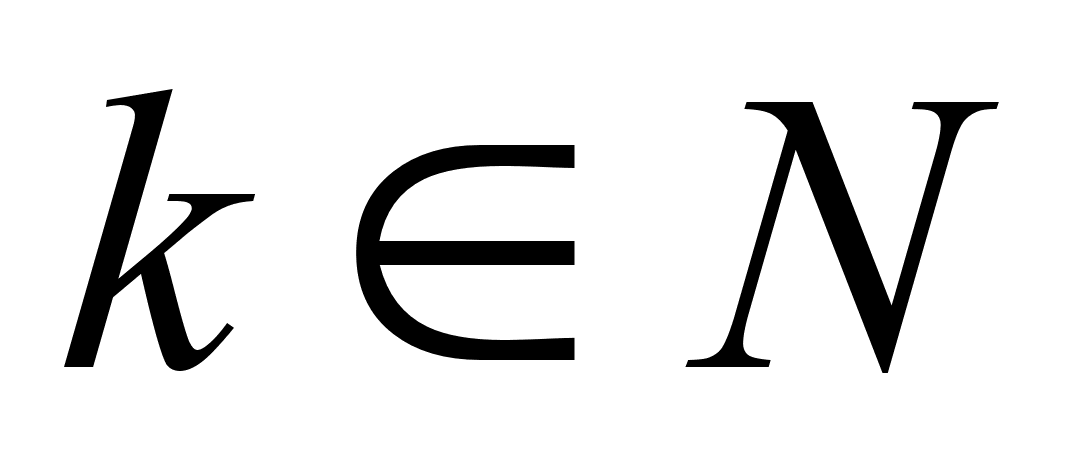 ,
начиная с
некоторого.
Если для таких
k
выполняется
неравенство
,
начиная с
некоторого.
Если для таких
k
выполняется
неравенство
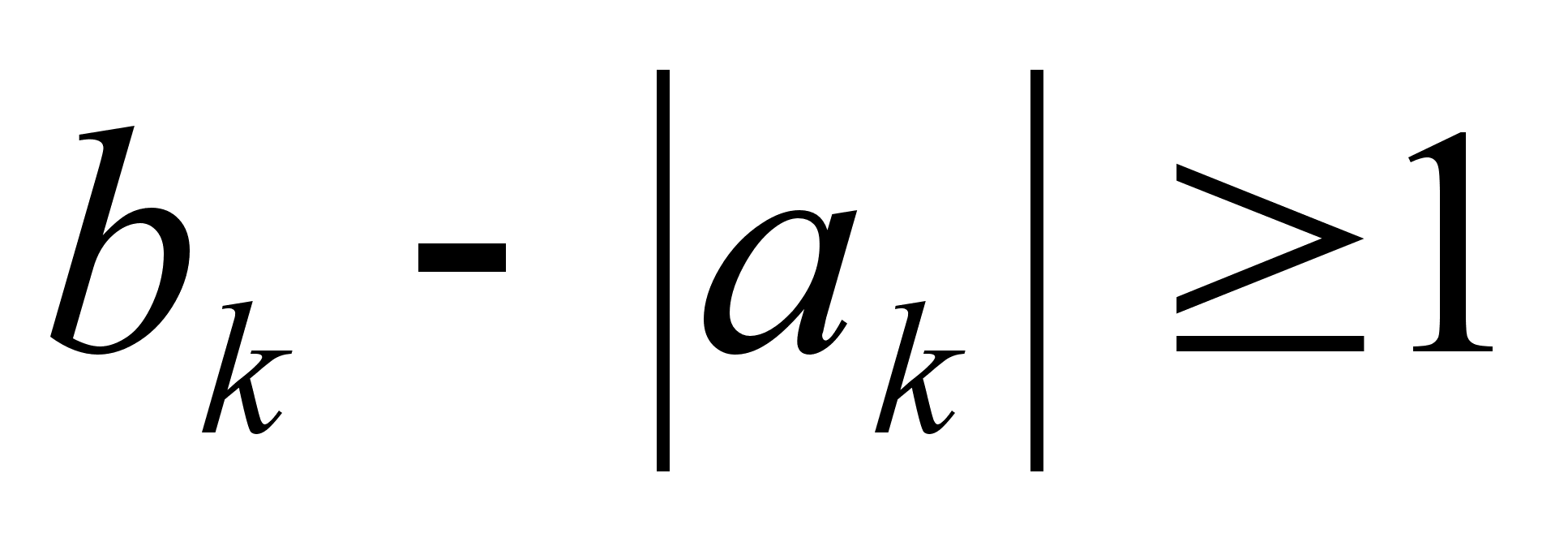 ,
то цепная дробь
сходится.
,
то цепная дробь
сходится.Пусть
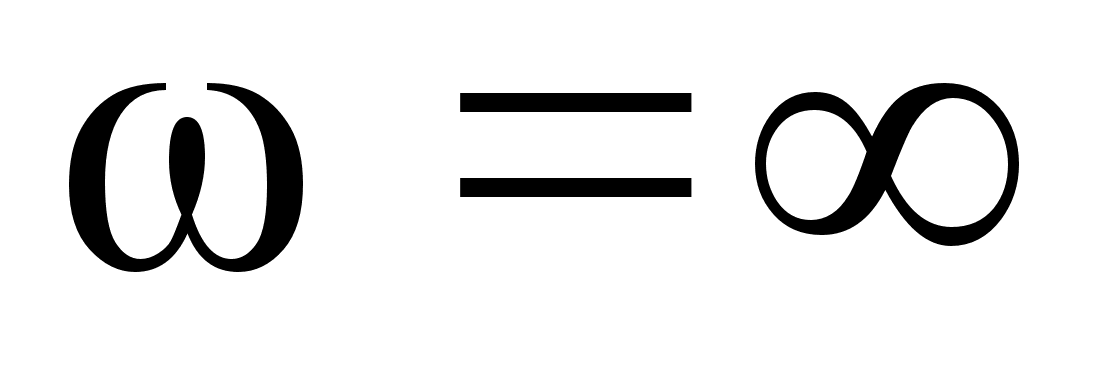 и все члены
последовательности
и все члены
последовательности
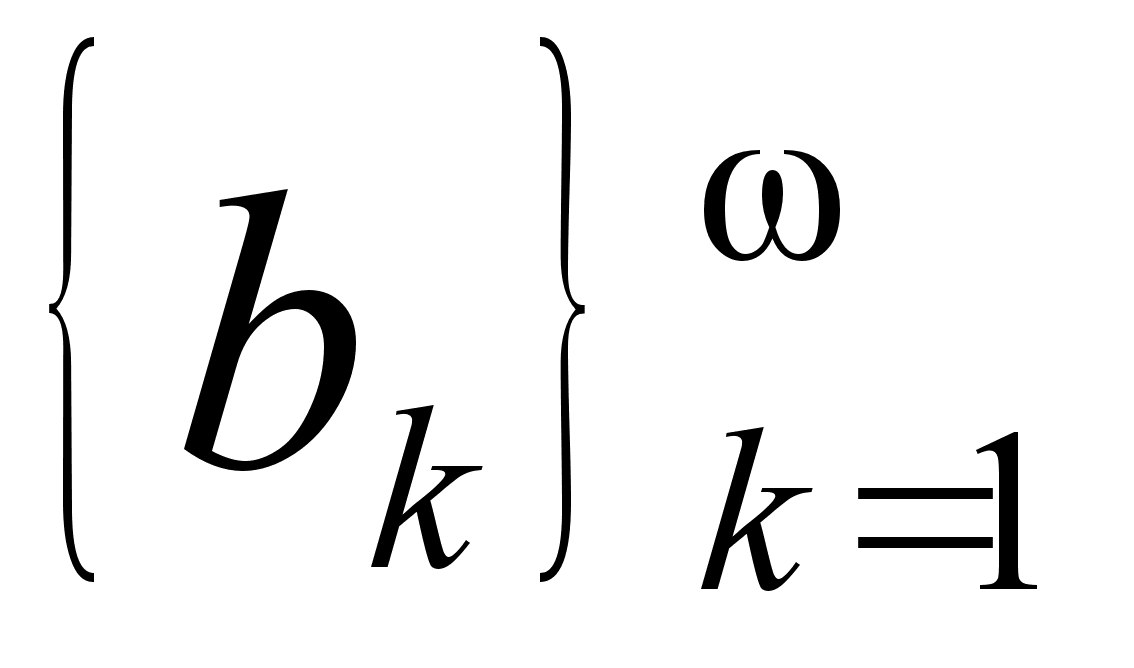 ,
начиная с
k=2
положительны.
Тогда цепная
дробь сходится
тогда и только
тогда, когда
ряд
,
начиная с
k=2
положительны.
Тогда цепная
дробь сходится
тогда и только
тогда, когда
ряд
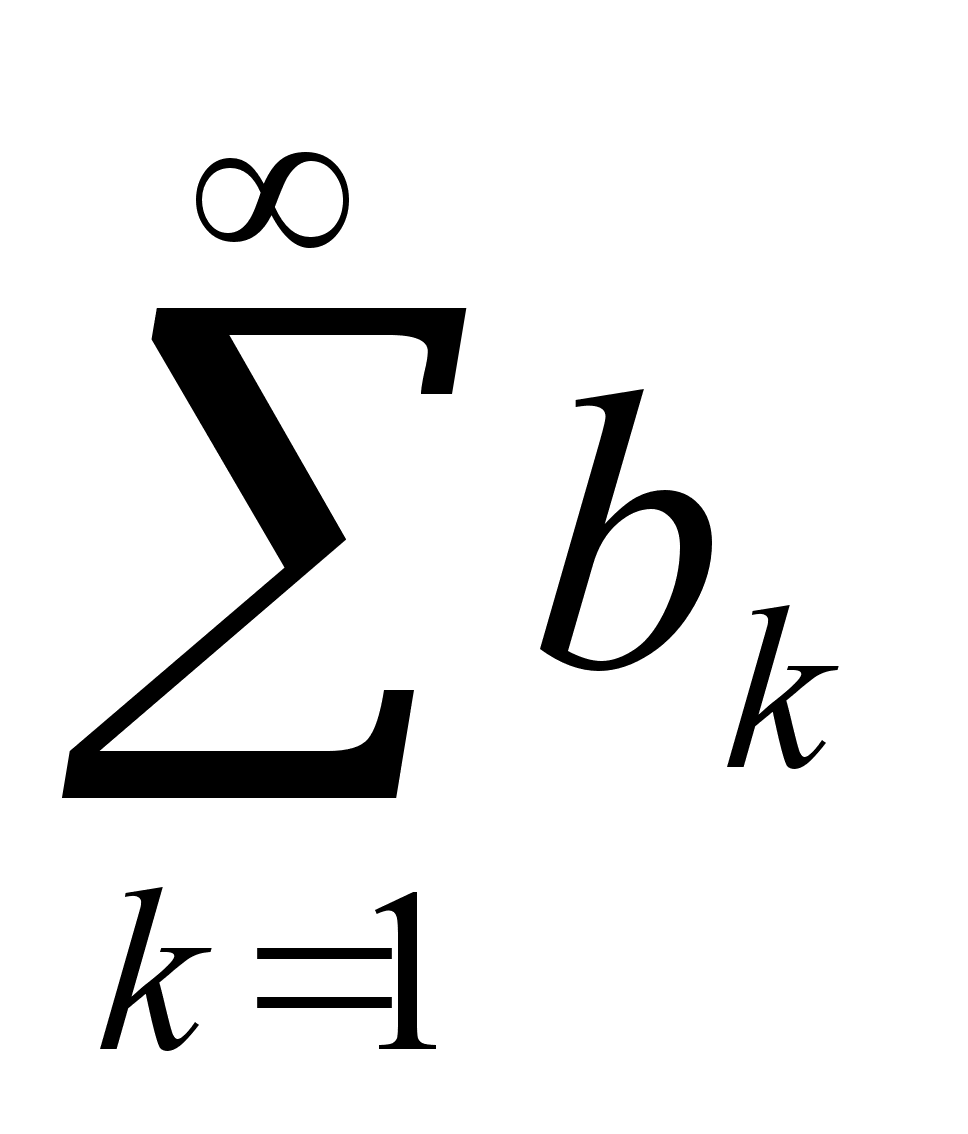 расходится
(теорема Зейделя).
расходится
(теорема Зейделя).
Интересной особенностью цепных дробей общего вида является то, что даже рациональные числа могут ими разлагаться в бесконечные цепные дроби. Например, имеется разложение
![]()
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
…
,
…
0,3; 0,42; 0,45; 0,467; …
Примечательно то, что квадратические иррациональности разлагаются и в непериодические цепные дроби общего вида.
Например, имеется разложение
![]()
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
…
,
…
1; 1,5; 1,38; 1,44; 1,40; …
Но самое
интересное
и важное это
то, что в то время
как до настоящего
времени неизвестно
разложение
в правильную
цепную дробь
ни одной алгебраической
иррациональности
степени выше
второй (другими
словами, неизвестны
общие свойства
неполных частных
таких разложений,
разложения
сами по себе
со сколь угодной
точностью можно
практически
найти), при помощи
общих цепных
дробей такие
разложения
находятся
довольно легко.
Отметим, например,
некоторые
разложения
и соответствующие
подходящие
дроби для
![]() :
:
![]()
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
…
,
…
1,33; 1,22; 1,284.
![]()
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
…
,
…
1,17; 1,25; 1,258; 1,2596; …
Приведем еще несколько примеров разложений других иррациональностей в цепные дроби общего вида:
![]()
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
…
,
…
Эта цепная
дробь для
![]() была найдена
еще более 300 лет
назад английским
математиком
Брункером.
была найдена
еще более 300 лет
назад английским
математиком
Брункером.
![]()
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
В 1776 году
И. Ламберт нашел
разложение
tg
x в
цепную дробь:
tg
x=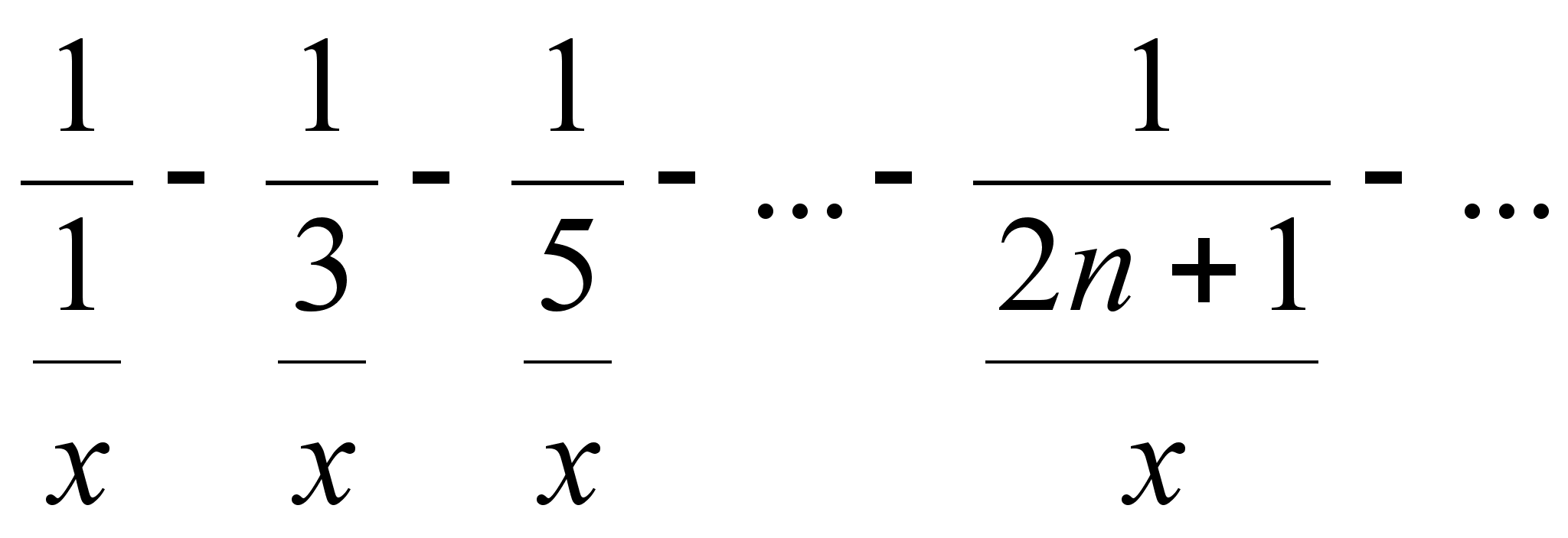
А. Лежандр
в предположении,
что эта цепная
дробь сходится,
показал, что
ее значение
для рациональных
значений
x
иррационально.
Принято считать,
что тем самым
была доказана
иррациональность
числа
![]() .
.
Л. Эйлер
нашел, что:
![]() =(1;
6, 10, 14, …).
Также Эйлер
нашел разложение
в цепную дробь
числа e.
e=(2;
1, 2, 1, 1, 4, 1, 1, 6, …),
то есть элементы
=(1;
6, 10, 14, …).
Также Эйлер
нашел разложение
в цепную дробь
числа e.
e=(2;
1, 2, 1, 1, 4, 1, 1, 6, …),
то есть элементы
![]() разложения
e
в цепную дробь
имеют вид:
разложения
e
в цепную дробь
имеют вид:
![]() ,
,
![]() ,
,
![]()
Швейцарский
математик
Иоганн Генрих
Ламберт (1728-1777) нашел
разложение
числа
![]() в виде цепной
дроби.
в виде цепной
дроби.
Первые
25 неполные частные
разложения
числа
![]() в правильную
цепную дробь
есть числа:
в правильную
цепную дробь
есть числа:
3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1.
Решение задач
Записать в виде конечной цепной дроби
a)
![]() ;
b)
;
b)
![]() ;
c)
;
c)
![]() 2,98976;
d)
2,98976;
d)
![]()
Решение:
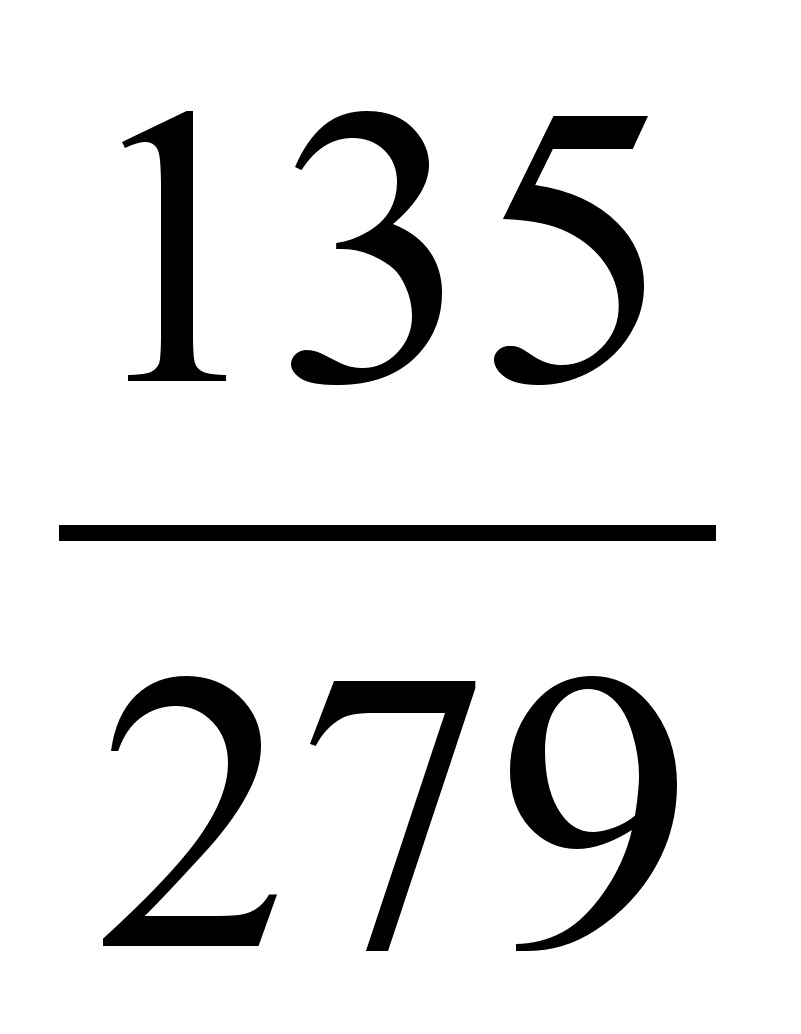 =(0,
2, 15);
=(0,
2, 15);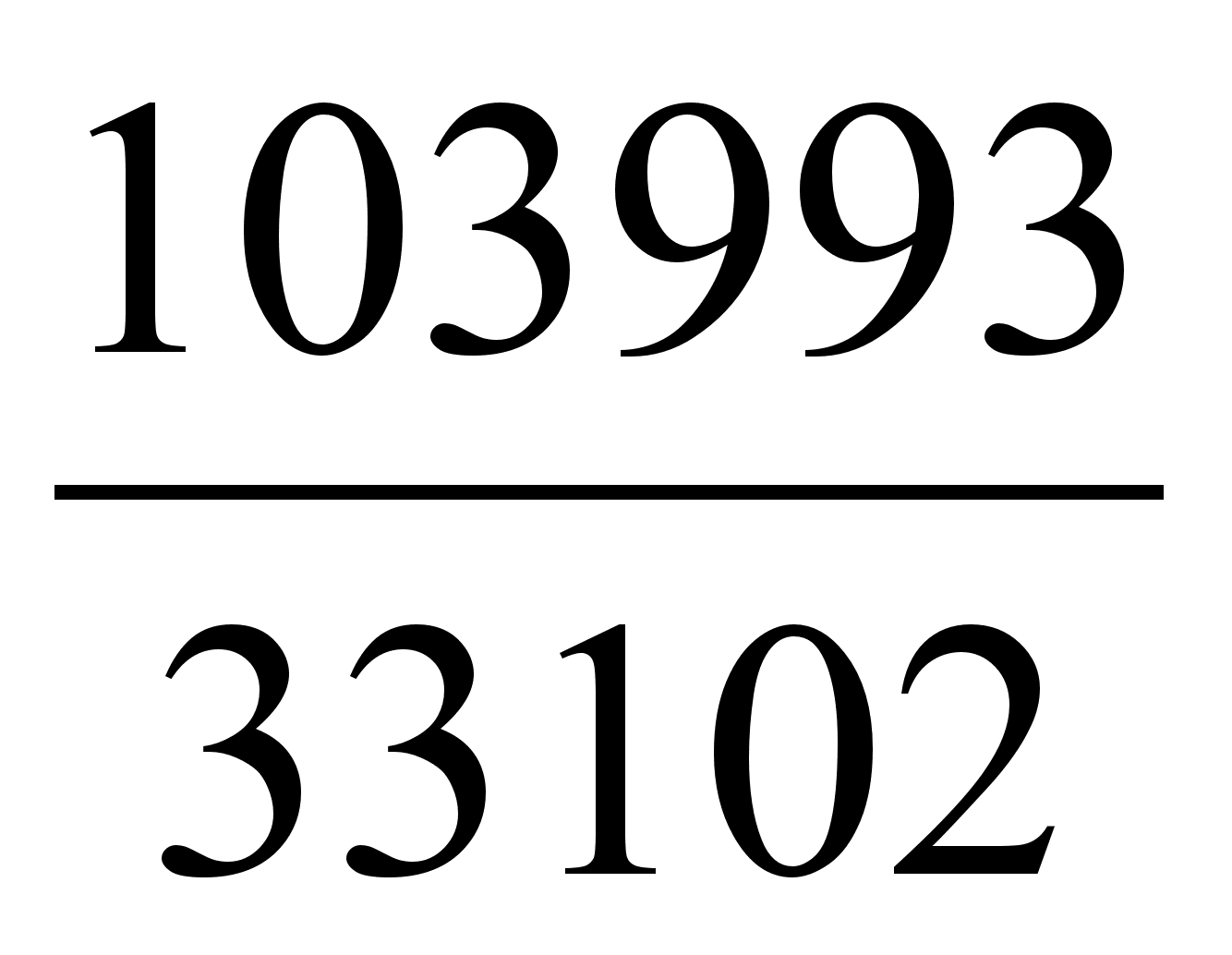 =(3,
7, 15, 1, 292);
=(3,
7, 15, 1, 292);2,98976=
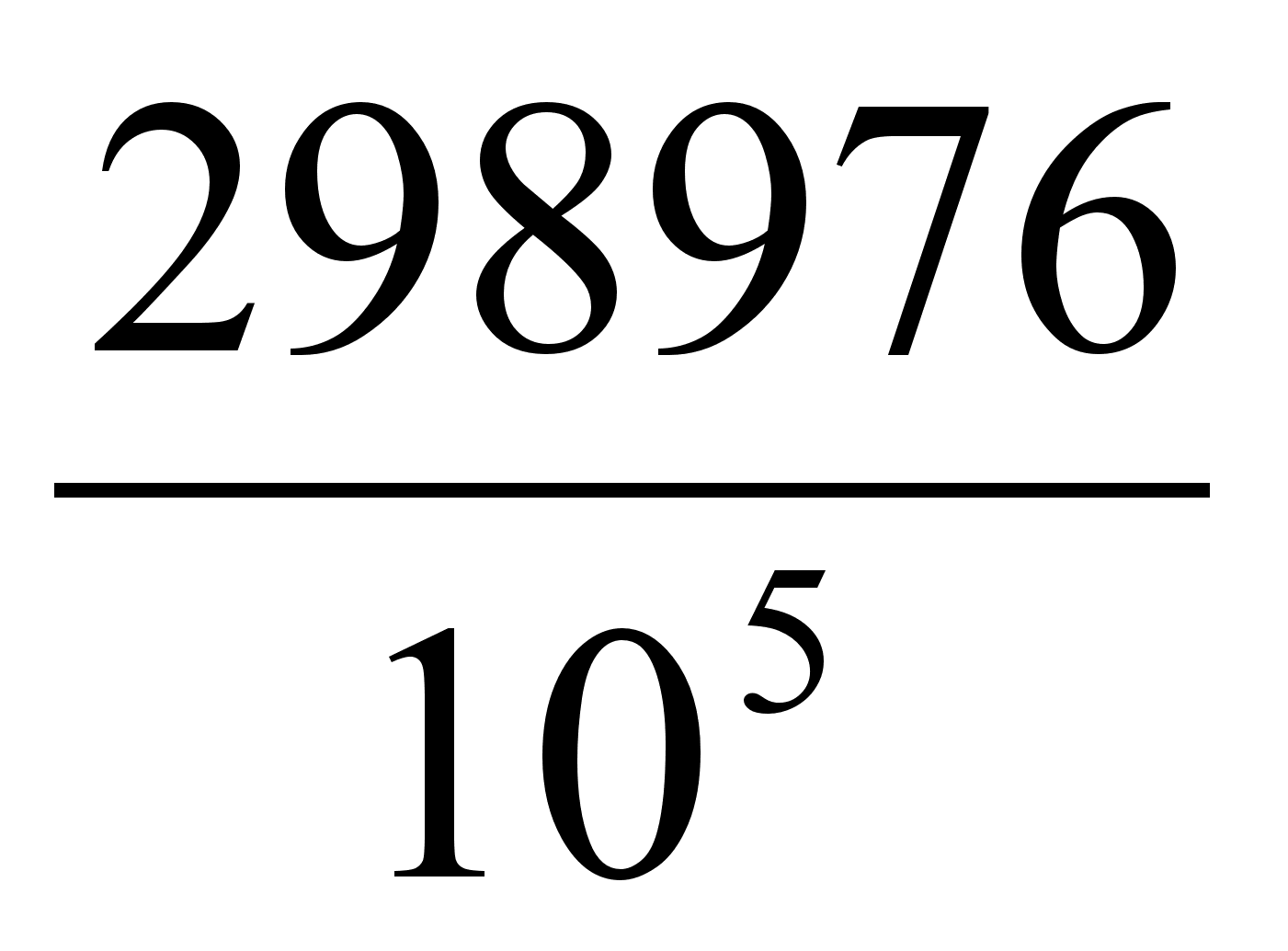 =(2,
1, 96, 1, 1, 1, 10);
=(2,
1, 96, 1, 1, 1, 10);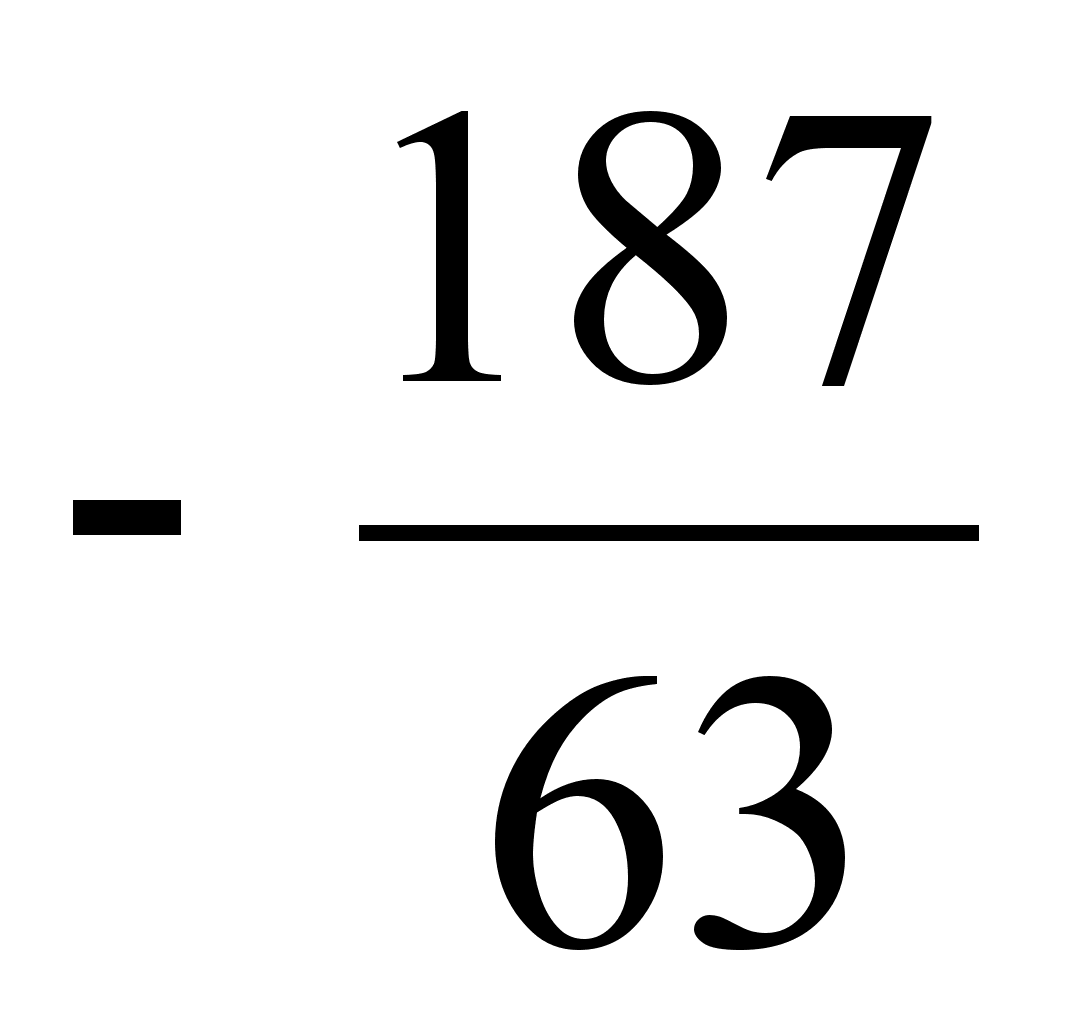 =–(2,
1, 30, 2)=(-2, 1, 30, 2)
=–(2,
1, 30, 2)=(-2, 1, 30, 2)
Разложить простую дробь в цепную дробь и найти ее подходящие дроби.
a)
![]() ;
b)
;
b)
![]() ;
c)
;
c)
![]() ;
d)
;
d)
![]()
Решение:
a)
![]() =(3,
2, 1, 24);
=(3,
2, 1, 24);
Находим подходящие дроби:
|
3 |
2 |
1 |
24 |
||
|
|
1 |
3 |
7 |
10 |
247 |
|
|
0 |
1 |
2 |
3 |
74 |
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]()
b)
![]() =(3,
3, 33);
=(3,
3, 33);
|
3 |
3 |
33 |
||
|
|
1 |
3 |
10 |
333 |
|
|
0 |
1 |
3 |
100 |
![]() =
=![]() ;
;
![]() =
=![]()
c)
![]() =
= =(3,
7, 15, 1, 292);
=(3,
7, 15, 1, 292);
|
3 |
7 |
15 |
1 |
292 |
||
|
|
1 |
3 |
22 |
333 |
355 |
103993 |
|
|
0 |
1 |
7 |
106 |
113 |
33102 |
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
;
d)
![]() =(0,
2, 2, 3);
=(0,
2, 2, 3);
|
0 |
2 |
2 |
3 |
||
|
|
1 |
0 |
1 |
2 |
7 |
|
|
0 |
1 |
2 |
5 |
17 |
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() .
.
3. Сократить дробь
a)![]() ;
b)
;
b)![]() ;
c)
;
c)![]()
Решение:
a)![]() ;
;
Разложим ее в конечную цепную дробь и найдем последнюю подходящую дробь для нее.
![]() =(4,
1, 1, 6)
=(4,
1, 1, 6)
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]()
Дробь
![]() несократима
и
несократима
и
![]() =
=![]() .
.
b)![]() =(0,
3, 3, 1, 6, 1, 3, 2)
=(0,
3, 3, 1, 6, 1, 3, 2)
![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]()
Дробь
![]() несократима
несократима
![]()
![]() =
=![]() .
.
c)![]() =(1,
1, 2, 2, 32)
=(1,
1, 2, 2, 32)
![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() - несократима
- несократима
![]()
![]() =
=![]() .
.
4. Найдите
первые четыре
подходящие
дроби разложения
в цепную дробь
числа
![]() =3,14159265…
=3,14159265…
![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]()
Ответ:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
5. Преобразуйте в обыкновенную дробь следующие цепные дроби: a) (2, 1, 1, 2, 1, 6, 2, 5); b) (2, 3, 1, 6, 4); c) (1, 3, 2, 4, 3, 1, 1, 1, 5);
d) (0, 3, 1, 2, 7).
Решение:
a) (2, 1, 1, 2, 1, 6, 2, 5)=![]()
Составим таблицу подходящих дробей:
|
2 |
1 |
1 |
2 |
1 |
6 |
2 |
5 |
|
|
|
2 |
3 |
5 |
13 |
18 |
121 |
260 |
1421 |
|
|
1 |
1 |
2 |
5 |
7 |
47 |
101 |
552 |
Ответ:
![]() =
=![]()
b)
(2, 3, 1, 6, 4)=
![]()
|
2 |
3 |
1 |
6 |
4 |
|
|
|
2 |
7 |
9 |
61 |
253 |
|
|
1 |
3 |
4 |
27 |
112 |
Ответ:
![]() =
=![]()
c) (1, 3, 2, 4, 3, 1, 1, 1, 5)
|
1 |
3 |
2 |
4 |
3 |
1 |
1 |
1 |
5 |
|
|
|
1 |
4 |
9 |
40 |
129 |
169 |
298 |
467 |
2633 |
|
|
1 |
3 |
7 |
31 |
100 |
131 |
231 |
362 |
2041 |
Ответ:
![]() =
=![]()
d)
(0, 3, 1, 2, 7)=![]()
|
0 |
3 |
1 |
2 |
7 |
|
|
|
0 |
1 |
1 |
3 |
22 |
|
|
1 |
3 |
4 |
11 |
81 |
Ответ:
![]() =
=![]()
6. Разложить в цепную дробь и заменить подходящей дробью с точностью до 0,001 следующие числа:
a)
![]() ;
b)
;
b)
![]() ;
c)
;
c)
![]() ;
d)
;
d)
![]() .
.
Решение:
a)
![]() =
=![]() .
Выделим
из
.
Выделим
из
![]() его целую часть:
его целую часть:
![]() ,
а дробную часть
,
а дробную часть
![]() -2,
которая
-2,
которая ![]() ,
где
,
где
![]() .
Повторяя эту
операцию выделения
целой части
и переворачивания
дробной, получаем:
.
Повторяя эту
операцию выделения
целой части
и переворачивания
дробной, получаем:
![]() ;
;
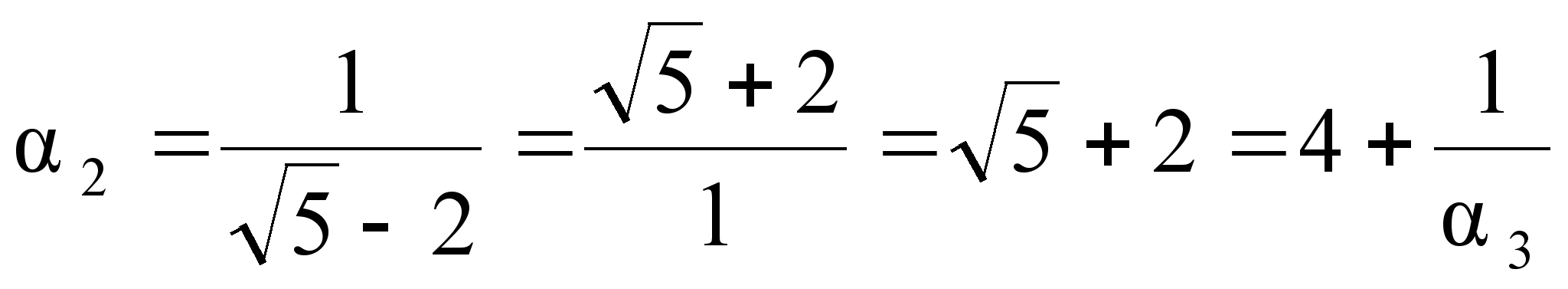 ;
;
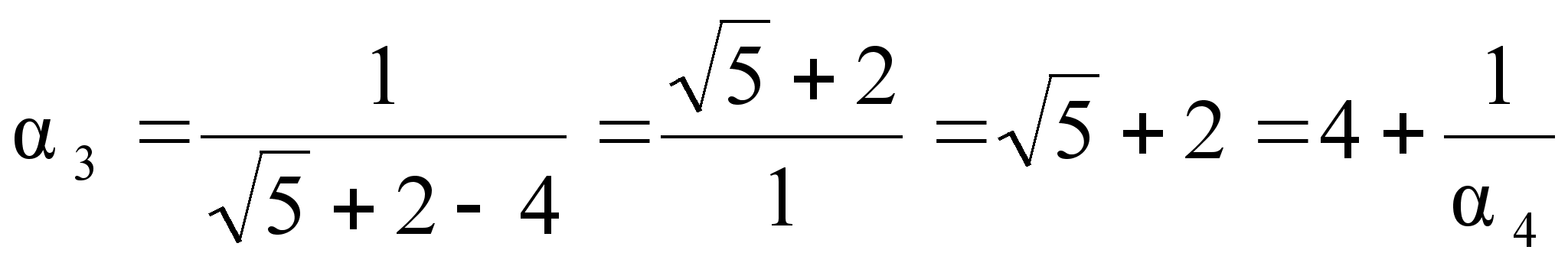 .
.
Мы
получили, что
![]() ,
следовательно,
неполные частные,
начиная с
,
следовательно,
неполные частные,
начиная с
![]() будут повторяться
и
будут повторяться
и
![]() =(2,
(4)).
=(2,
(4)).
Составим таблицу подходящих дробей:
|
2 |
4 |
4 |
4 |
… | |
|
|
2 |
9 |
38 |
||
|
|
1 |
4 |
17 |
72 |
Нам
необходимо
найти такую
подходящую
дробь
![]() ,
чтобы
,
чтобы
![]() .
Очевидно, что
это
.
Очевидно, что
это
![]() ,
так как 17·72>1000.
,
так как 17·72>1000.
Ответ:
![]() .
.
b)
![]() =
=![]() ;
;
![]() =5
=5
![]() ;
;
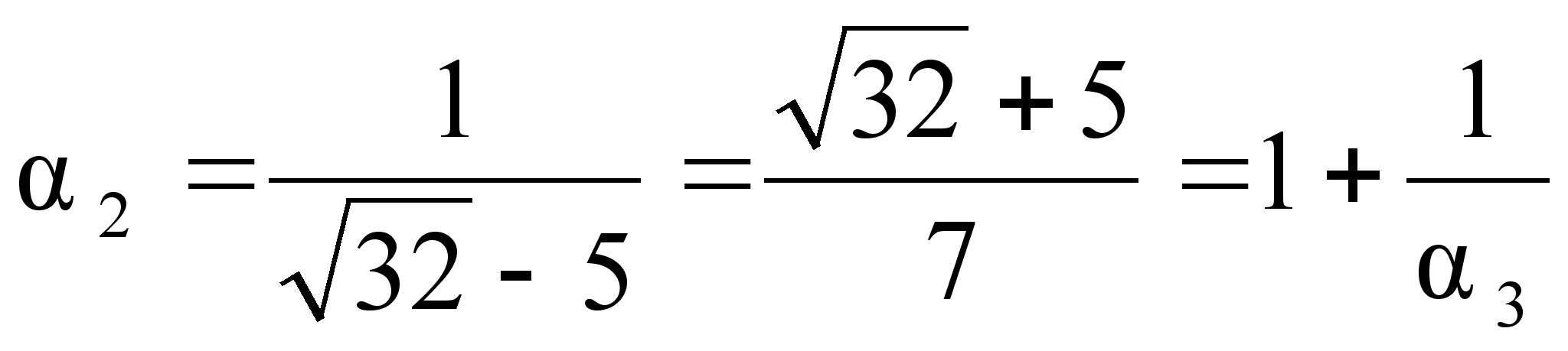 ;
;
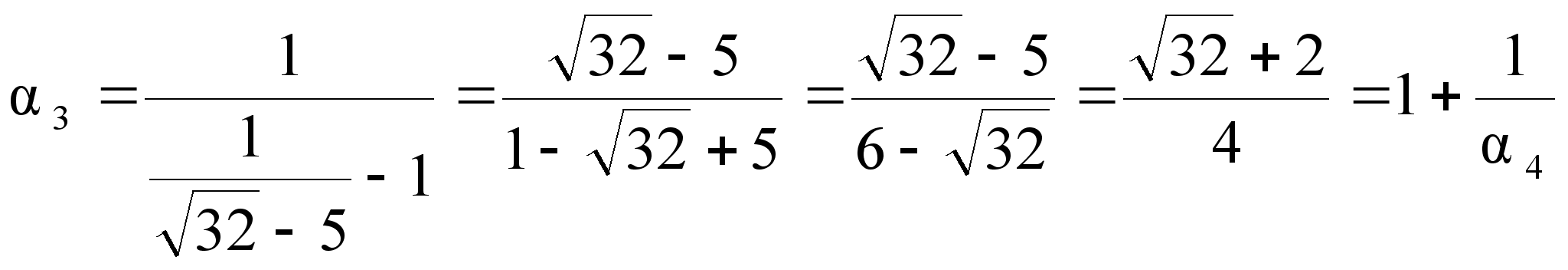 ;
;
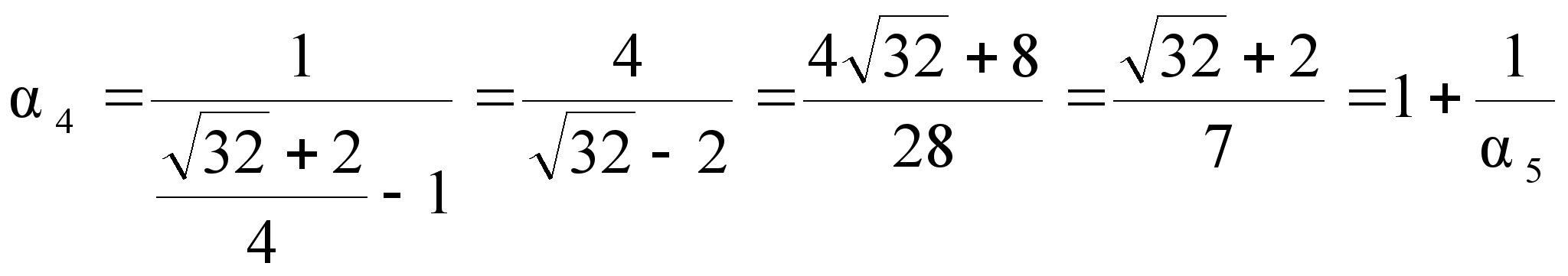 ;
;
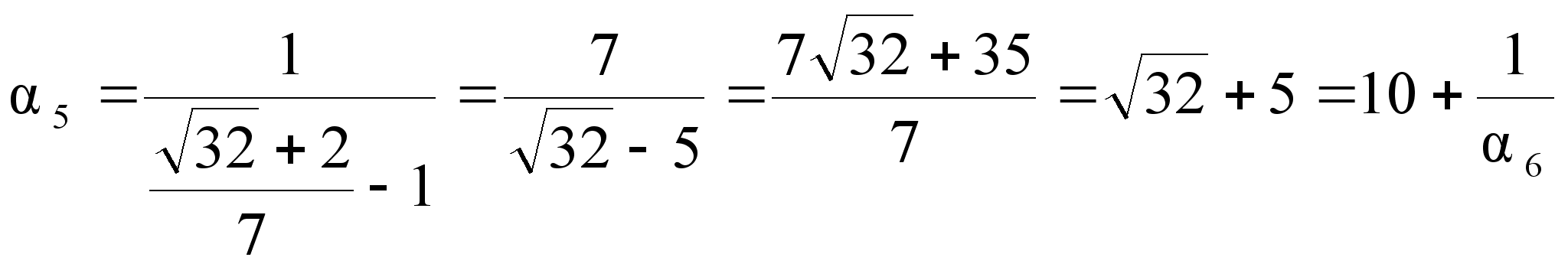 ;
;
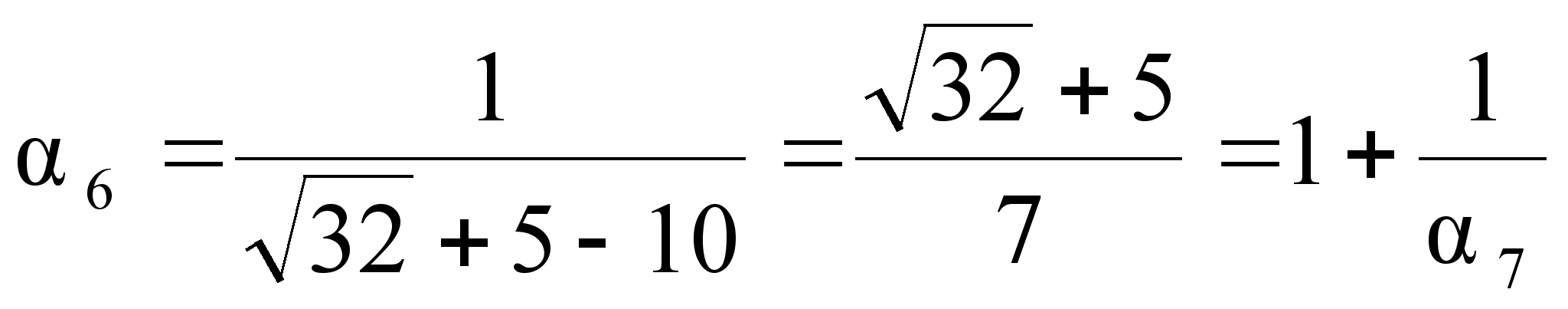 .
.
Мы
получили
![]() неполные
частные, начиная
с
неполные
частные, начиная
с
![]() будут повторяться
и
будут повторяться
и
![]() =(5,
(1, 1, 1, 10)).
=(5,
(1, 1, 1, 10)).
|
5 |
1 |
1 |
1 |
10 |
1 |
… | |
|
|
5 |
6 |
11 |
17 |
181 |
198 |
|
|
|
1 |
1 |
2 |
3 |
32 |
35 |
![]() ,
так как 32·35>1000.
Ответ:
,
так как 32·35>1000.
Ответ:
![]() .
.
c)
![]() =(3,
2, 5, 2, 7, 2);
=(3,
2, 5, 2, 7, 2);
|
3 |
2 |
5 |
2 |
7 |
2 |
|
|
|
3 |
7 |
38 |
83 |
619 |
1321 |
|
|
1 |
2 |
11 |
24 |
179 |
382 |
![]() ,
так как 24·179>1000.
,
так как 24·179>1000.
Ответ:
![]() .
.
d)
![]() =
=![]() ;
;
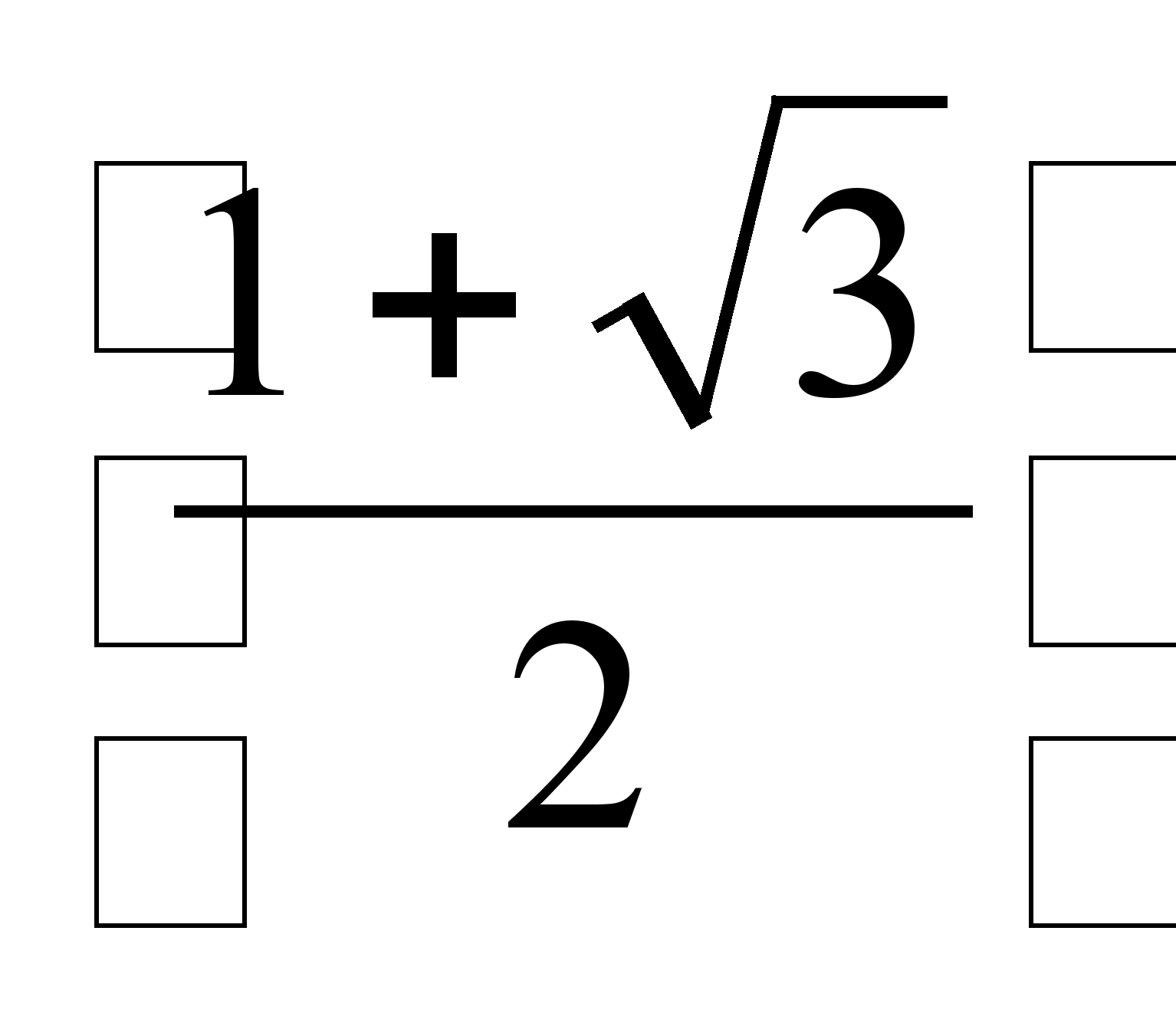 =1
=1
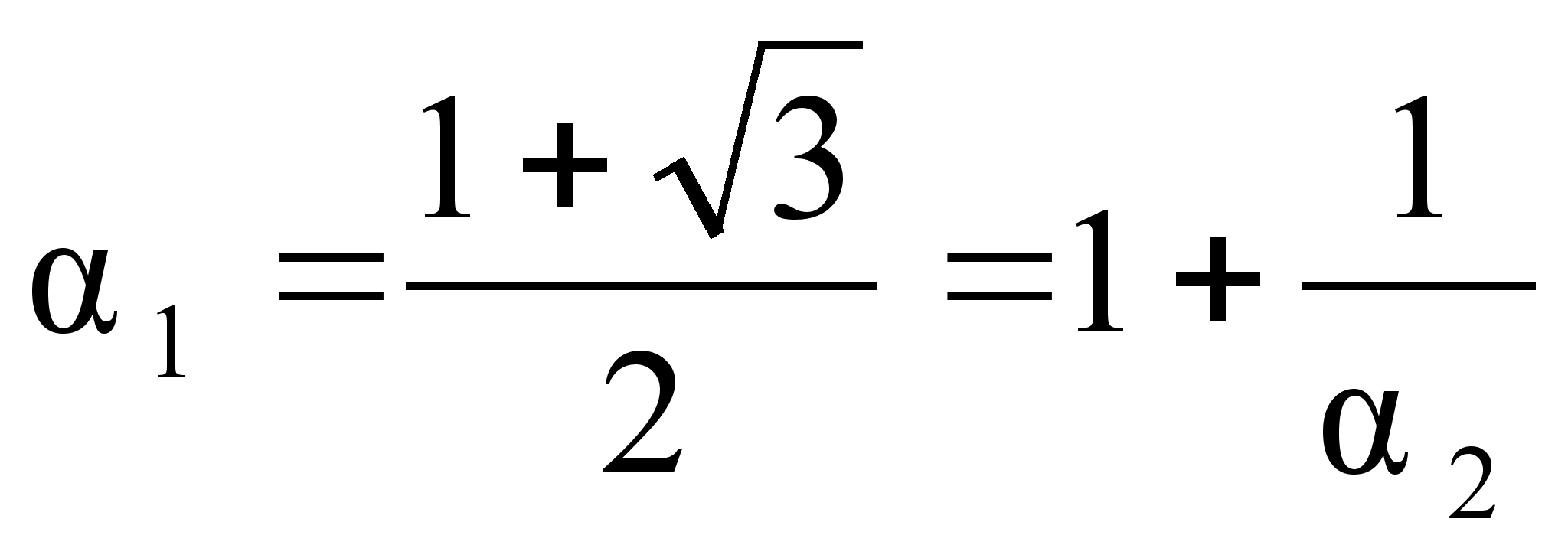 ;
;
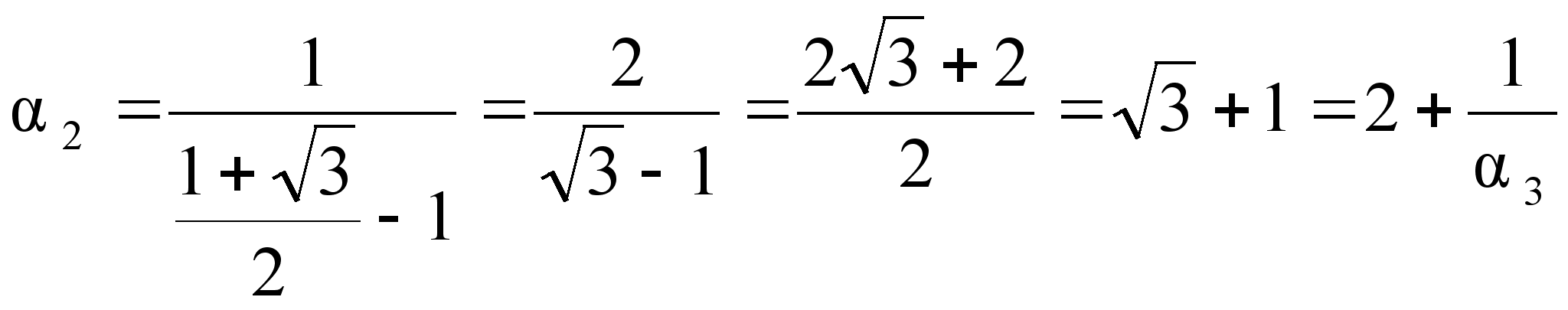 ;
;
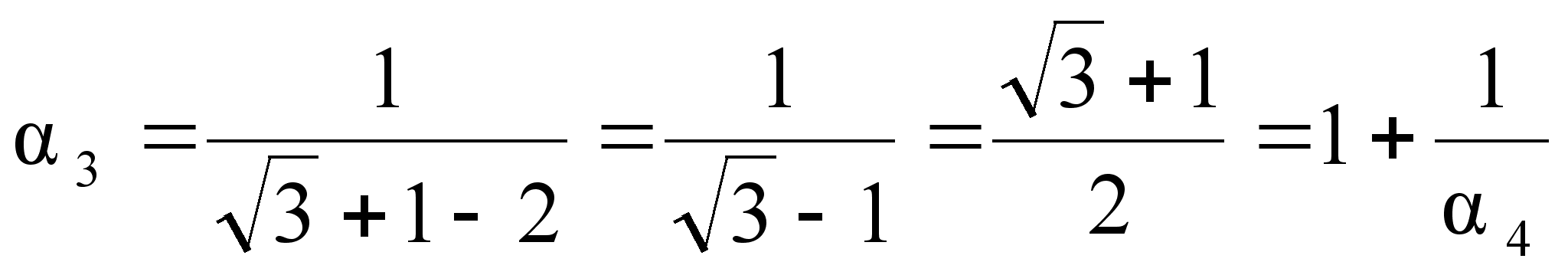 ;
;
![]()
![]() =((1,
2))
=((1,
2))
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
|
|
|
1 |
3 |
4 |
11 |
15 |
41 |
56 |
153 |
|
|
|
1 |
2 |
3 |
8 |
11 |
30 |
41 |
102 |
![]() ,
так как 30·41>1000.
,
так как 30·41>1000.
Ответ:
![]() .
.
7. Найти действительные числа, которые обращаются в данные цепные дроби:
a) (4, (3, 2, 1)); b) ((2, 1))
Решение:
a) (4, (3, 2, 1)) - смешанная периодическая дробь.
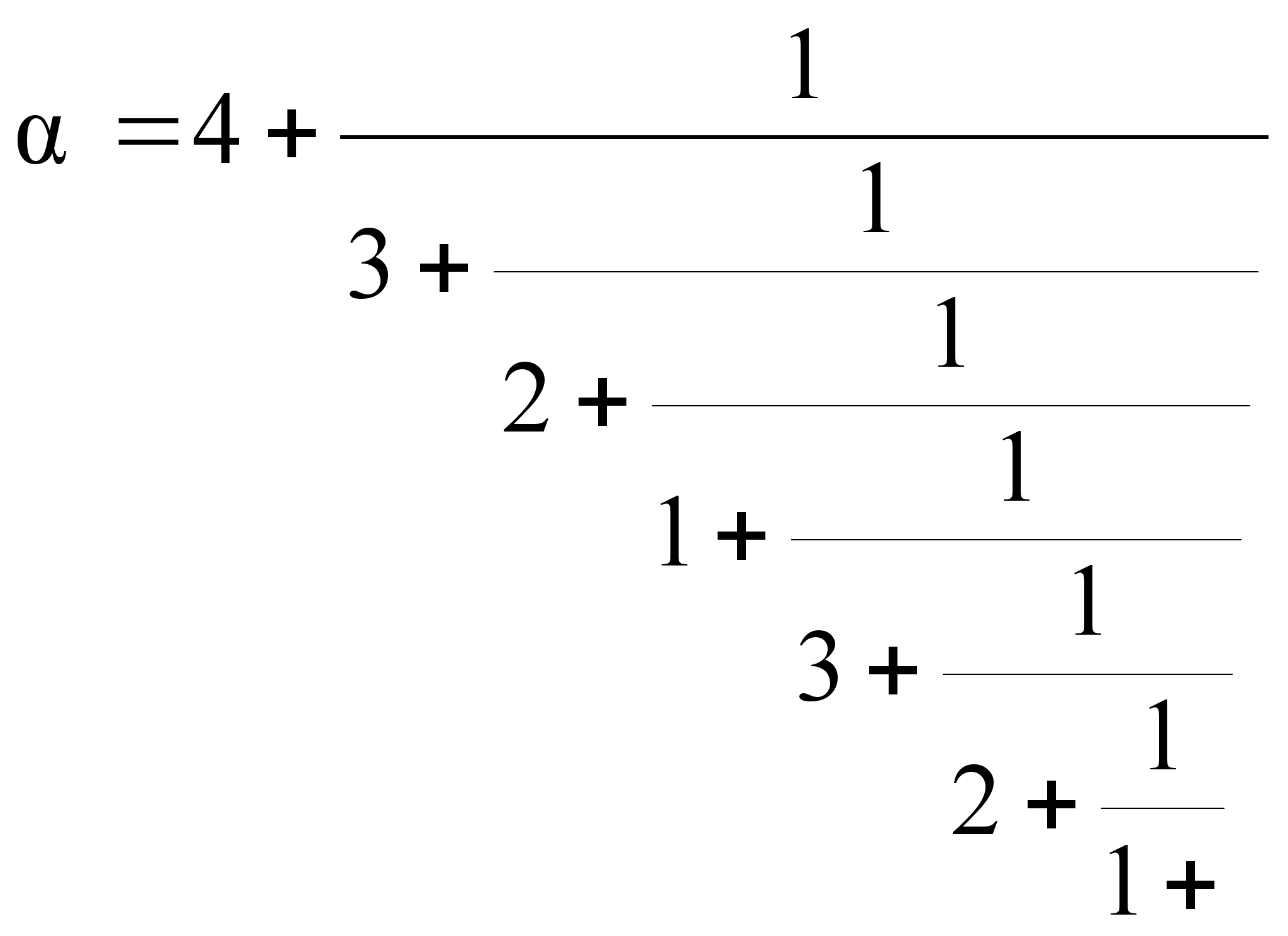
![]() ,
то есть
,
то есть
![]() ,
где
,
где
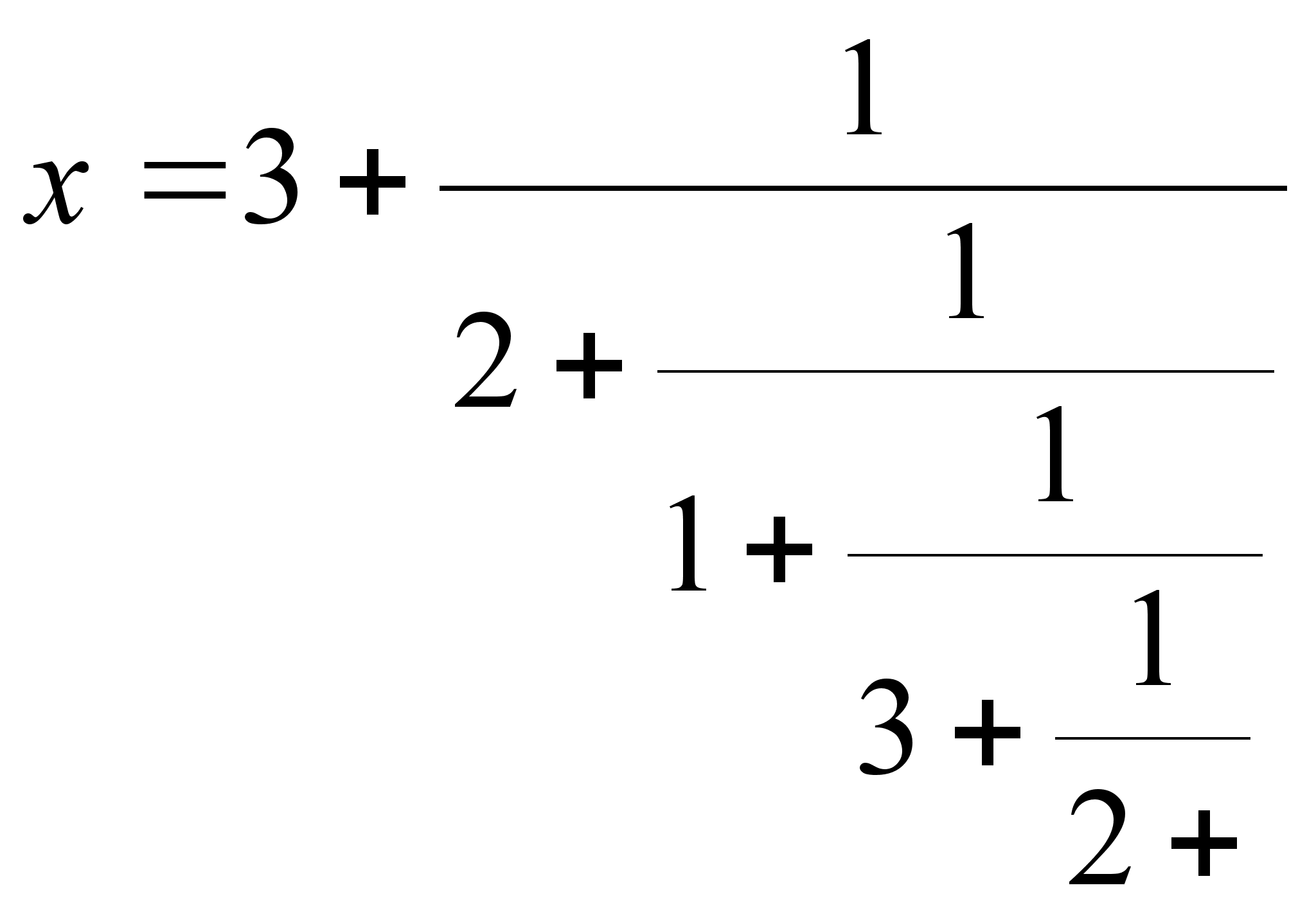
![]()
x=((3, 2, 1)) - чисто периодическая цепная дробь. Так как выражение, начинающееся с четвертого неполного частного 3, имеет тот же вид:
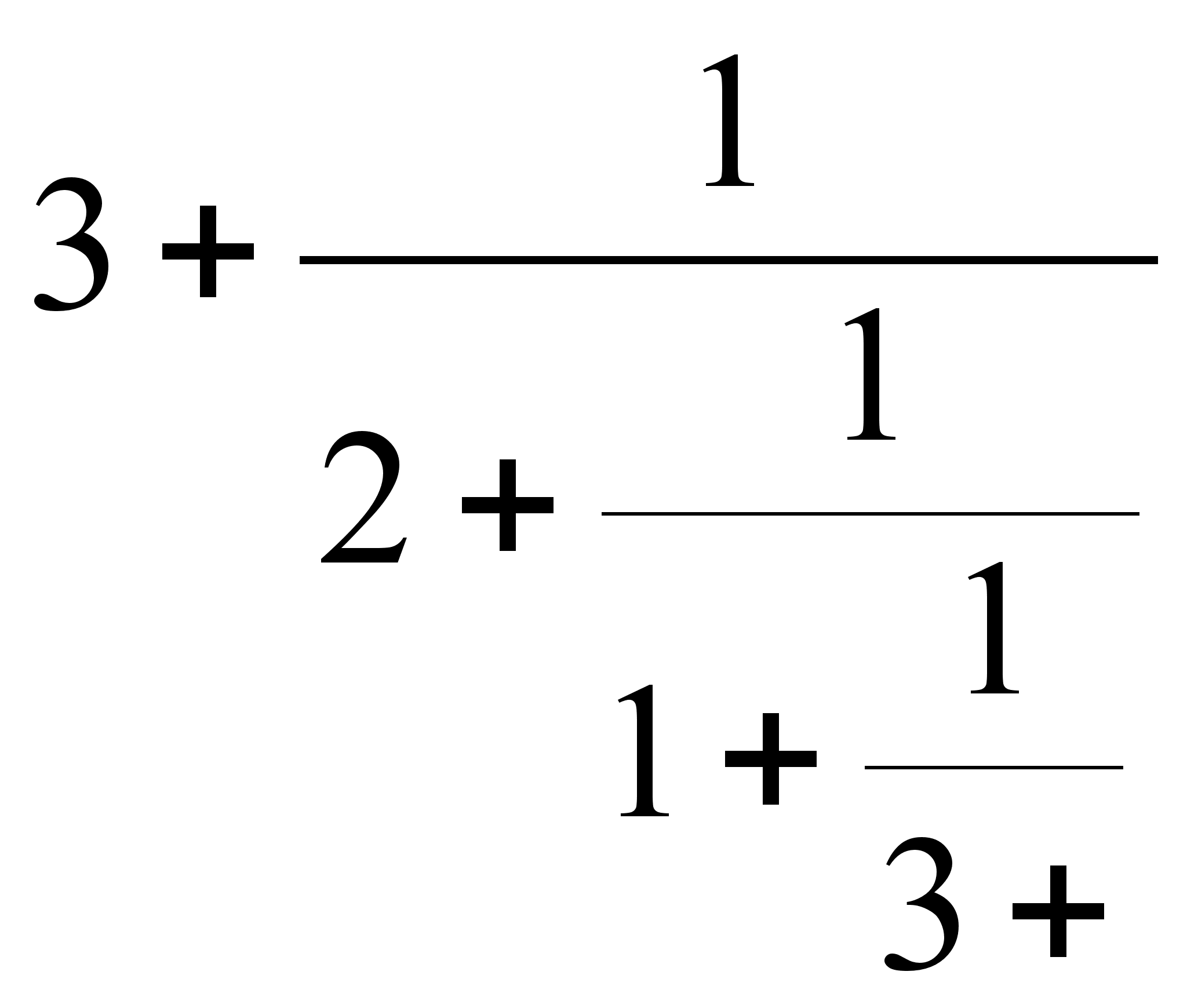
![]() ,
то мы можем
записать x=(3,
2, 1, x)=
,
то мы можем
записать x=(3,
2, 1, x)=
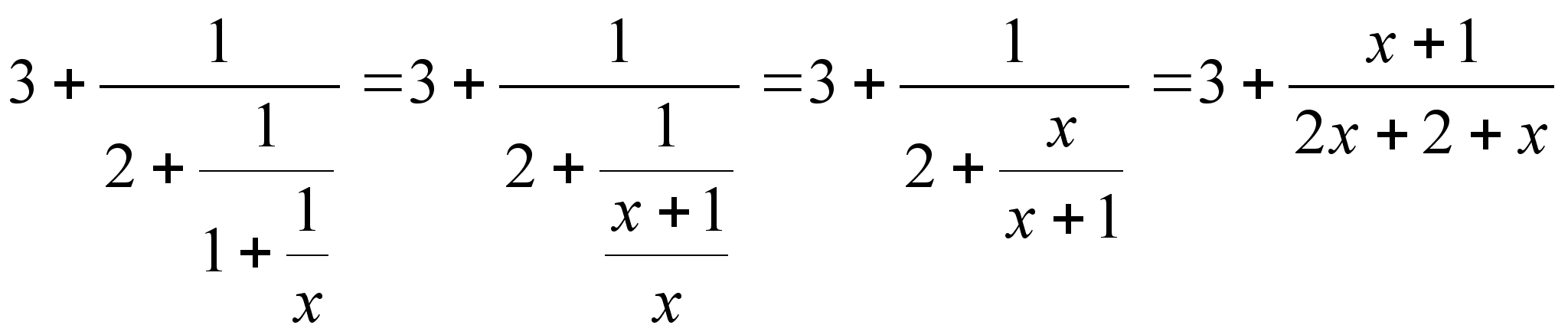 =
=![]() ,
после чего
приходим к
квадратному
уравнению
относительно
x:
,
после чего
приходим к
квадратному
уравнению
относительно
x:
![]()
![]()
D=64+12·7=148
![]() .
.
Положительное
решение и есть
x.
![]() .
Найдем
.
Найдем
![]() .
.
![]() =4+
=4+![]() =
=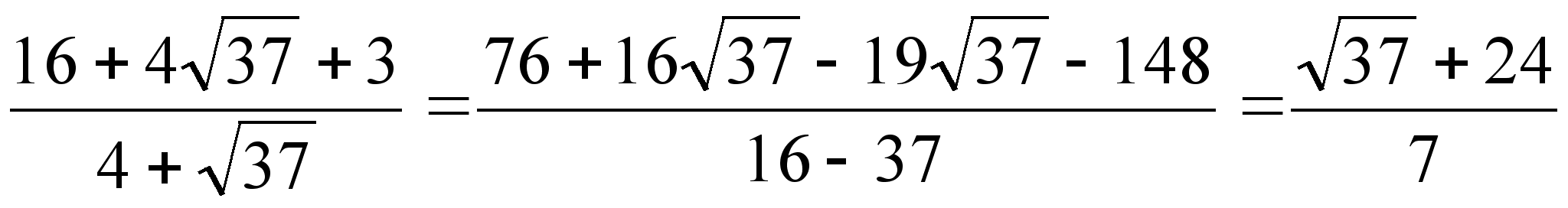
Ответ:
![]() .
.
b)
((2, 1))=![]()
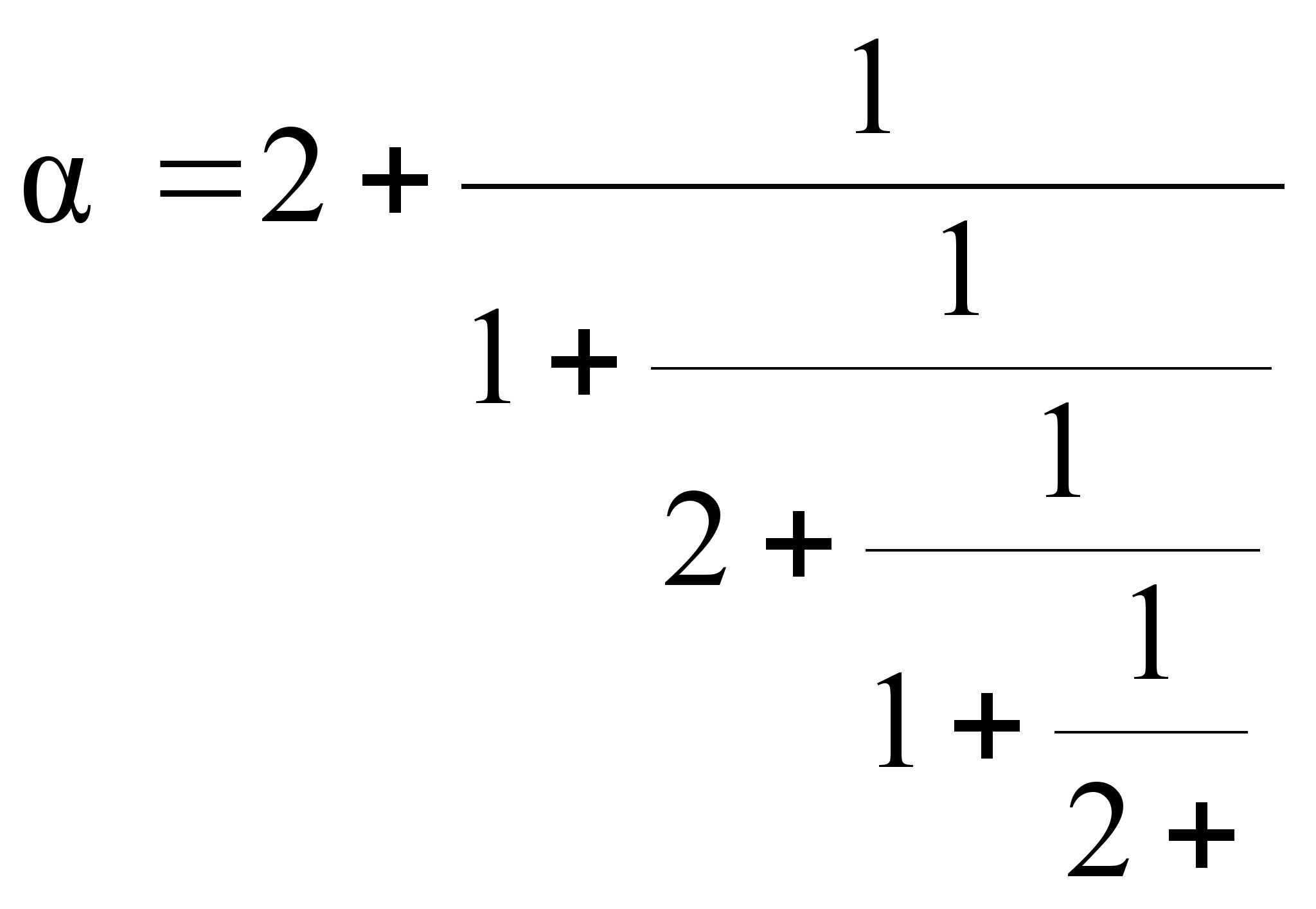
![]() =(2,
1,
=(2,
1,
![]() )
)
![]()
Сейчас мы можем найти таким же путем, как и в задаче a), но можно решить задачу легче. Составим таблицу подходящих дробей:
|
2 |
1 |
|
|
|
|
2 |
3 |
3 |
|
|
1 |
1 |
|
![]() =
=![]()
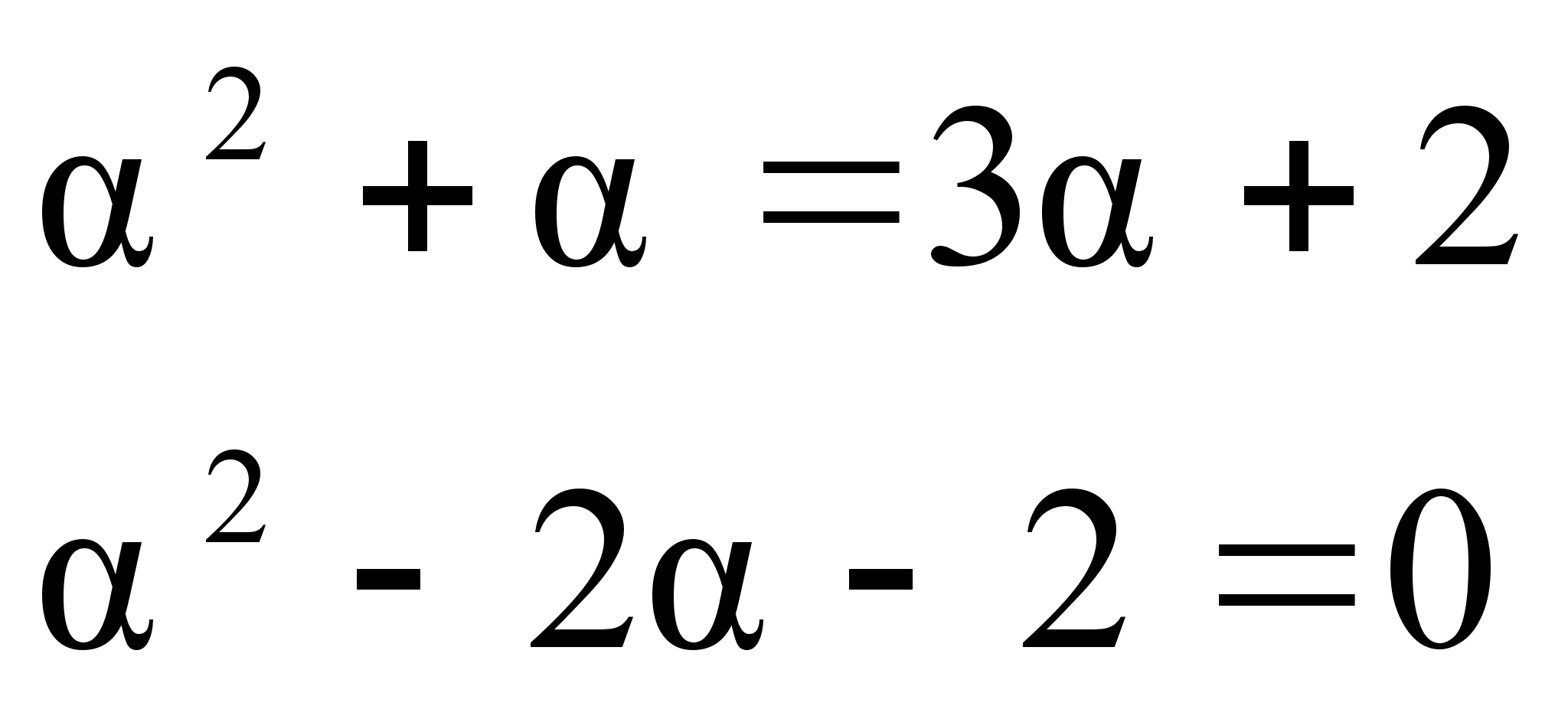
D=4+4·2=12
![]()
Положительное
решение и есть
искомое
![]() .
.
Ответ:
![]() .
.
8. Решить в целых числах уравнения:
a) 143x+169y=5; b) 2x+5y=7; c) 23x+49y=53.
Решение:
a) 143x+169y=5 - диофантово уравнение.
(143, 169)=13(НОД находим с помощью алгоритма Евклида)
![]() уравнение
решений не
имеет.
уравнение
решений не
имеет.
Ответ:
![]() .
.
b) 2x+5y=7
(2,
5)=1
![]() уравнение
имеет решение
в целых числах.
уравнение
имеет решение
в целых числах.
Разложим
![]() в цепную дробь.
в цепную дробь.
![]() =(0,
2, 2). Составим
все подходящие
дроби.
=(0,
2, 2). Составим
все подходящие
дроби.
![]() ;
;
![]() ;
;
![]()
На
основании
свойства подходящих
дробей
![]() получим
получим
2·2-1·5
=(-1)3
или
2·2+5(-1)=-1
![]()
2·(-14)+5·7=7,
то есть
![]()
![]() – частное решение.
– частное решение.
Все решения могут быть найдены по формулам
![]() или
или
![]()
c) 23x+49y=53
(23,
49)=1
![]() существуют
целые решения.
существуют
целые решения.
![]() =(0,
2, 7, 1, 2)
=(0,
2, 7, 1, 2)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
17·23-8·49=(-1)5
23·17+49·(-8)=-1
![]()
23·(-901)+49·424=53
![]()
![]()
![]() или
или
![]()
9. Разложите число 150 на два положительных слагаемых, одно из которых кратно 11, а второе – 17.
Решение: Пусть 11x – первое число 11x>0 x>0;17y - второе число 17y>0 y>0.
Тогда 11x+17y=150
(11,
17)=1![]() существуют
решения.
существуют
решения.
(11, 17)=(0, 1, 1, 1, 5)
|
0 |
1 |
1 |
1 |
5 |
|
|
|
0 |
1 |
1 |
2 |
11 |
|
|
1 |
1 |
2 |
3 |
17 |
11·3-2·17=(-1)5=–1
11·3+17·(-2)=-1
![]()
11·(-450)+17·300=150
x=-450+27·17=9![]() 99
- первое
число
99
- первое
число
y=300-11·27=3![]() 51
- второе
число.
51
- второе
число.
Ответ: 99; 51.
10. Решить уравнения Пелля:
a)
![]() b)
b)
![]()
Решение:
a)
![]()
Представим
![]() в виде цепной
дроби:
в виде цепной
дроби:
![]()
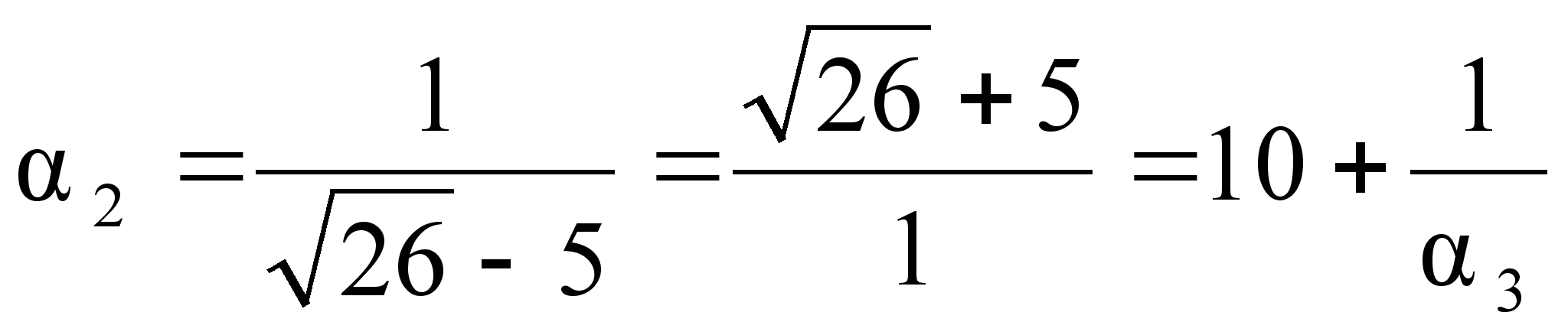
![]()
![]()
![]() =(5,
(10)).
=(5,
(10)).
Количество
чисел в периоде
нечетное (одна)
![]()
![]() =(5;
10)=
=(5;
10)=![]() .
.
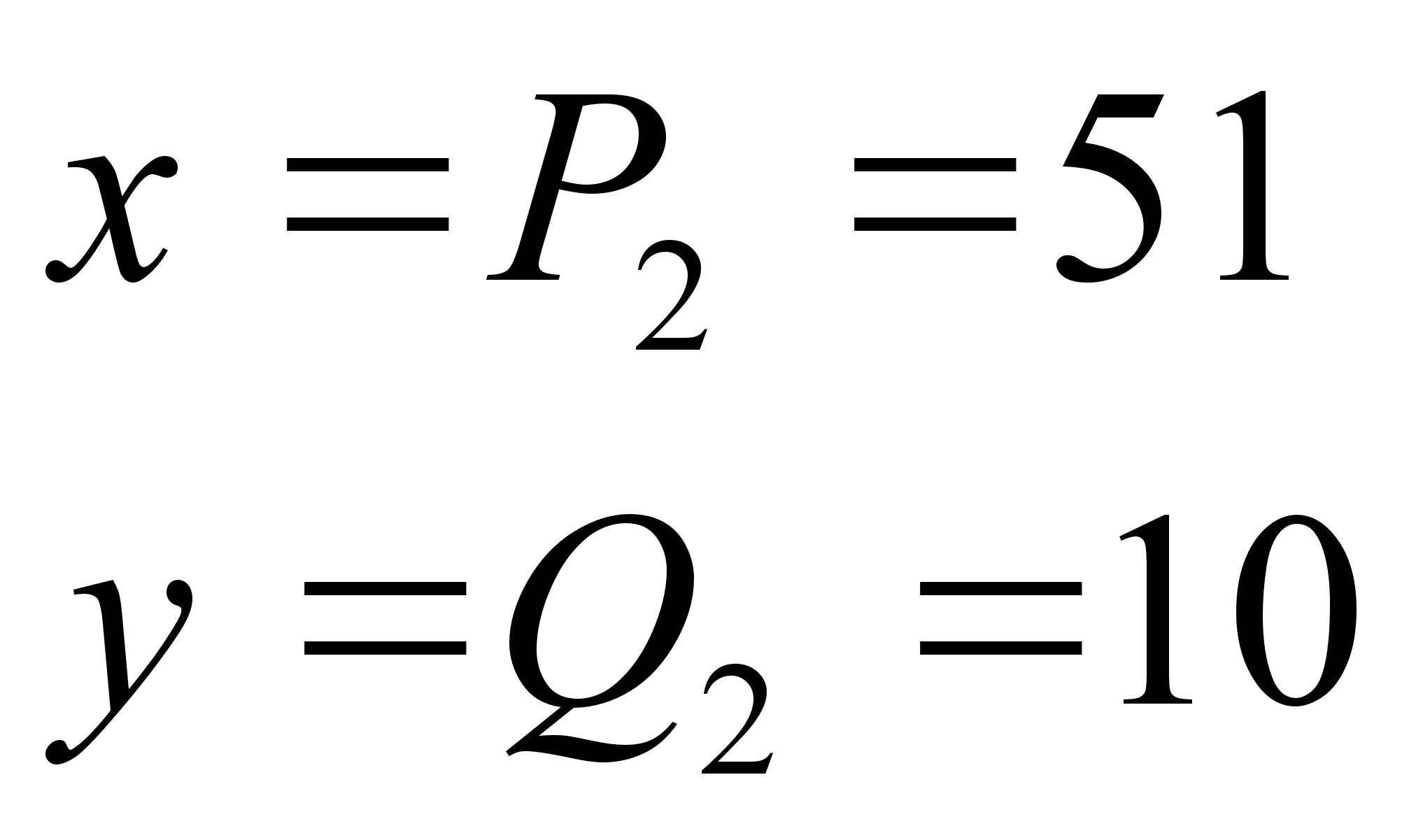 - наименьшее
положительное
решение.
- наименьшее
положительное
решение.
Ответ: x=51, y=10.
b)
![]()
![]()
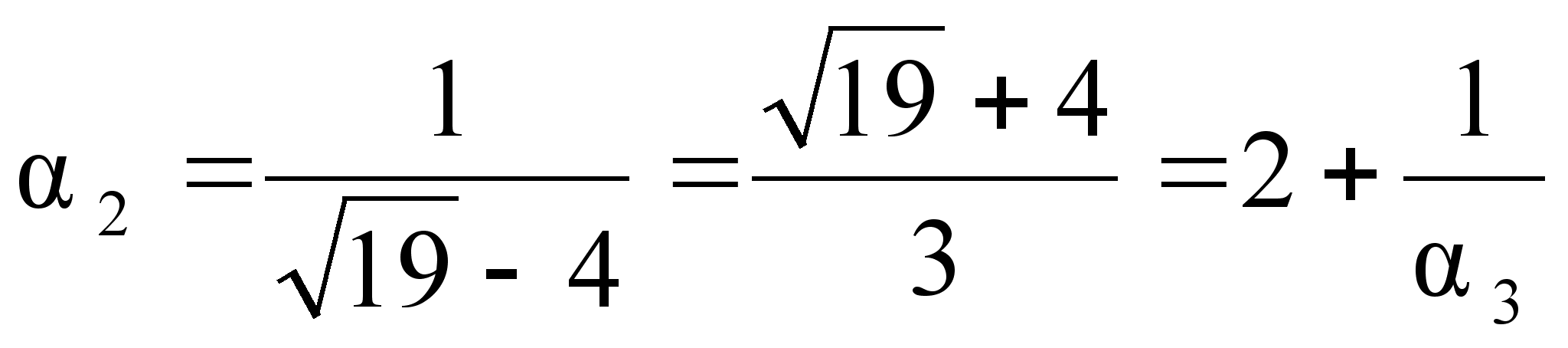

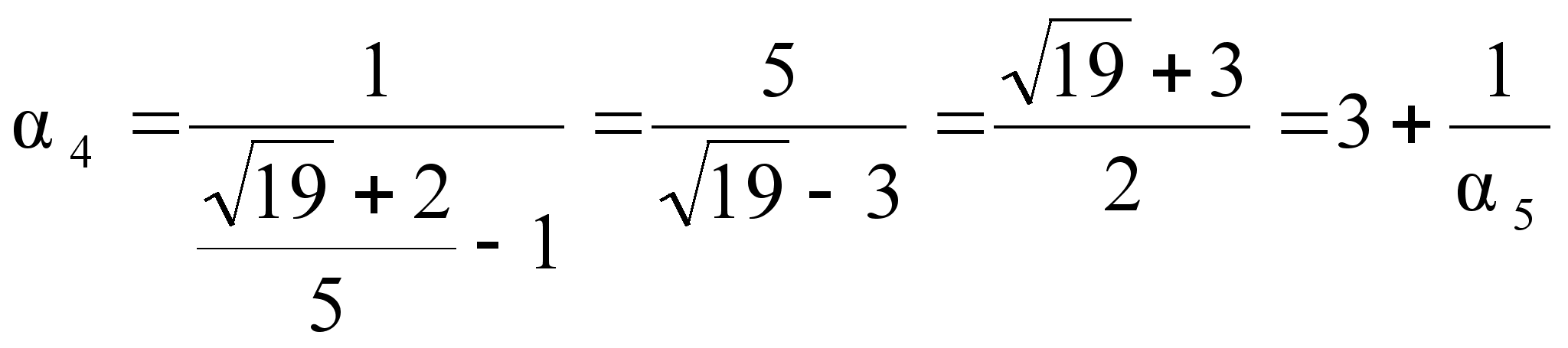
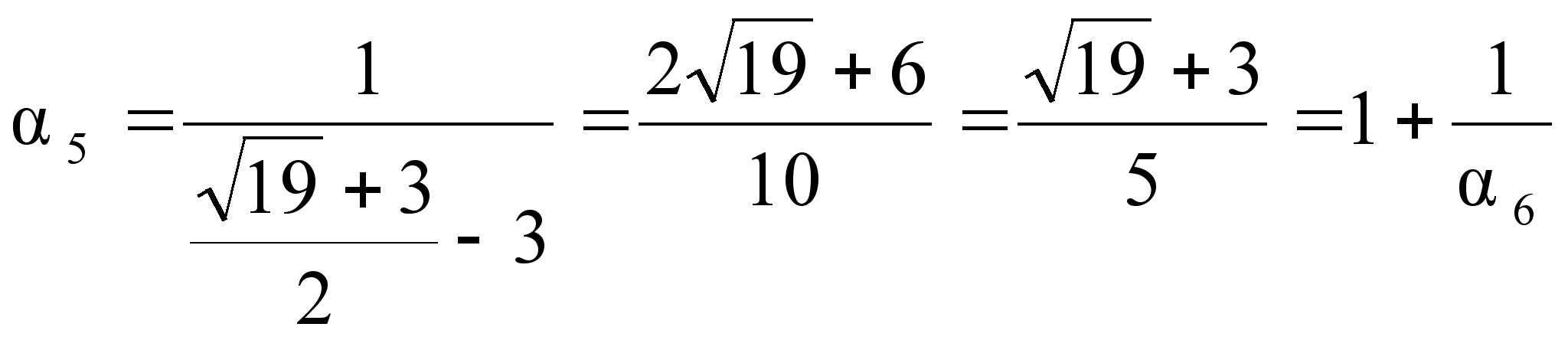
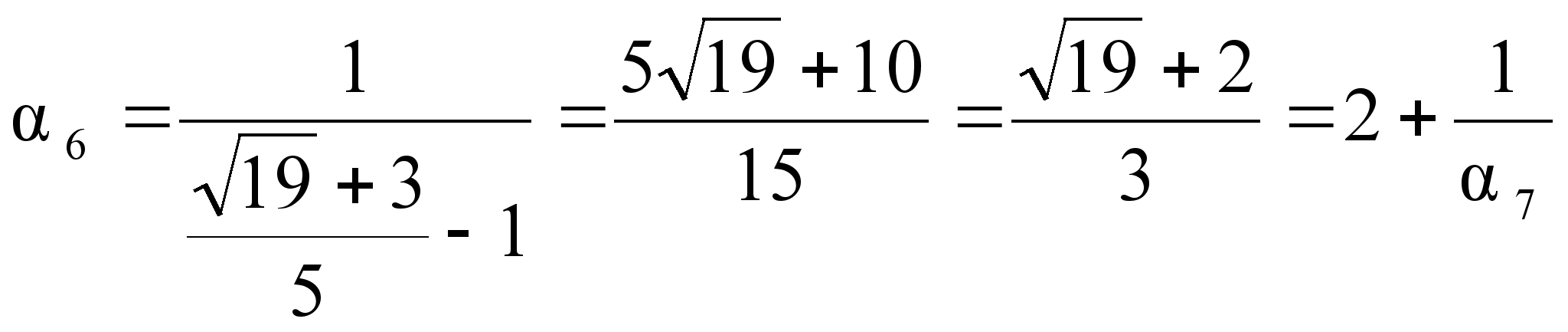
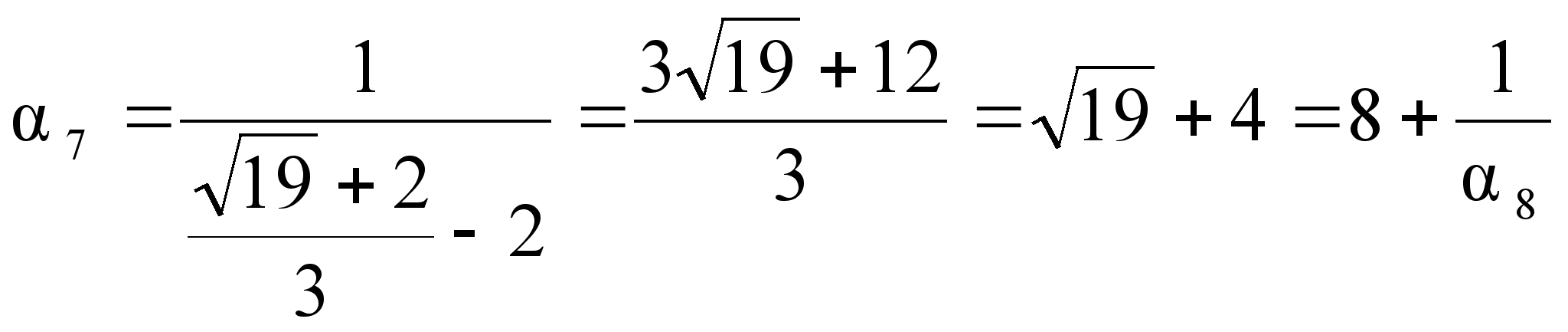
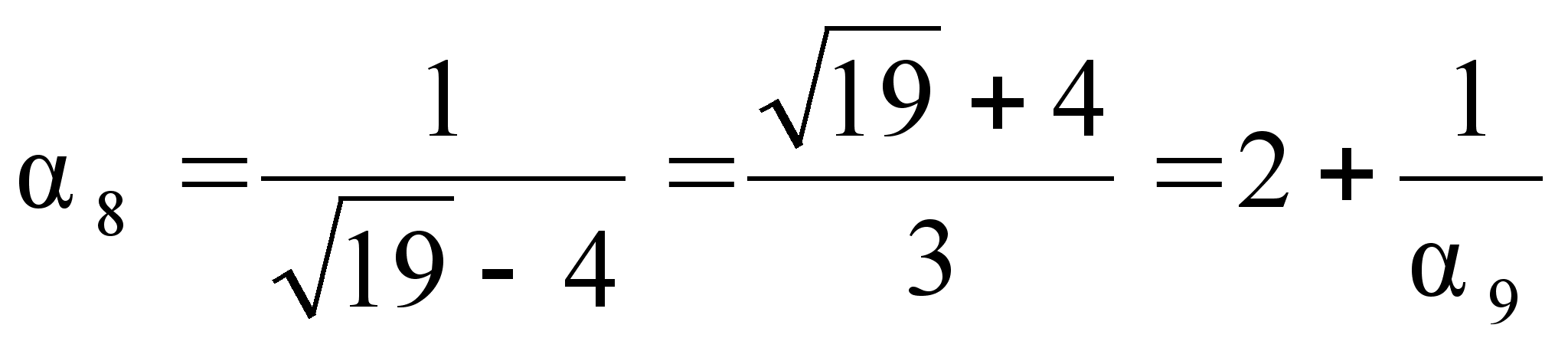
![]()
![]() =(4,
(2, 1, 3, 1, 2, 8))
=(4,
(2, 1, 3, 1, 2, 8))
Количество чисел в периоде четное (шесть)
|
4 |
2 |
1 |
3 |
1 |
2 |
|
|
|
4 |
9 |
13 |
48 |
61 |
170 |
|
|
1 |
2 |
3 |
11 |
14 |
39 |
![]()
Ответ: x=170, y=39.
Заключение
Данная курсовая работа показывает значение цепных дробей в математике.
Их можно успешно применить к решению неопределенных уравнений вида ax+by=c. Основная трудность при решении таких уравнений состоит в том, чтобы найти какое-нибудь его частное решение. Так вот, с помощью цепных дробей можно указать алгоритм для разыскания такого частного решения.
Цепные дроби можно применить и к решению более сложных неопределенных уравнений, например, так называемого уравнения Пелля:
![]() (
(![]() ).
).
Бесконечные цепные дроби могут быть использованы для решения алгебраических и трансцендентных уравнений, для быстрого вычисления значений отдельных функций.
В настоящее время цепные дроби находят все большее применение в вычислительной технике, ибо позволяют строить эффективные алгоритмы для решения ряда задач на ЭВМ.
Литература:
1. М.Б. Балк, Г.Д. Балк. Математика после уроков. М, «Просвещение», 71.
2. А.А. Бухштаб. Теория чисел. М, «Просвещение», 96.
Алгебра и теория чисел. Под редакцией Н.Я. Виленкина, М, «Просвещение», 84.
И.М. Виноградов. Основы теории чисел. М, «Наука», 72.
А.А. Кочева. Задачник-практикум по алгебре и теории чисел. М, «Просвещение», 84.
Л.Я. Куликов, А.И. Москаленко, А.А. Фомин. Сборник задач по алгебре и теории чисел. М, «Просвещение», 93.
Е.С. Ляпин, А.Е. Евсеев. Алгебра и теория чисел. М, «Просвещение», 74.
Математическая энциклопедия, том V, М, «Советская энциклопедия», 85.
Ш.Х. Михелович. Теория чисел. М, «Высшая школа», 67.