
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Реферат: Исследование явления дисперсии электромагнитных волн в диэлектриках
Реферат: Исследование явления дисперсии электромагнитных волн в диэлектриках
Содержание.
Введение........................................................................................................................3
§ 1. Материальные уравнения электромагнитного поля в среде с дисперсией.....5
§ 2. Закон дисперсии. Вектор объемной плотности поляризации.........................10
§ 3. Зависимость показателя преломления и поглощения от частоты..................12
Заключение.................................................................................................................15
Литература..................................................................................................................16
Введение.
Важнейшей
характеристикой
линейной
распределенной
системы является
закон дисперсии,
который связывает
волновое число
и частоту
монохроматической
волны. Он может
быть записан
как
![]() ,
,
![]() или в неявной
форме
или в неявной
форме
![]() .
.
Когда плоская
волна описывается
одним (вообще
говоря, интегродифференциальным)
уравнением,
закон дисперсии
получают, отыскивая
его решение
в виде
![]() .
В простейшем
случае процесс
распространения
волны описывается
уравнением
.
В простейшем
случае процесс
распространения
волны описывается
уравнением
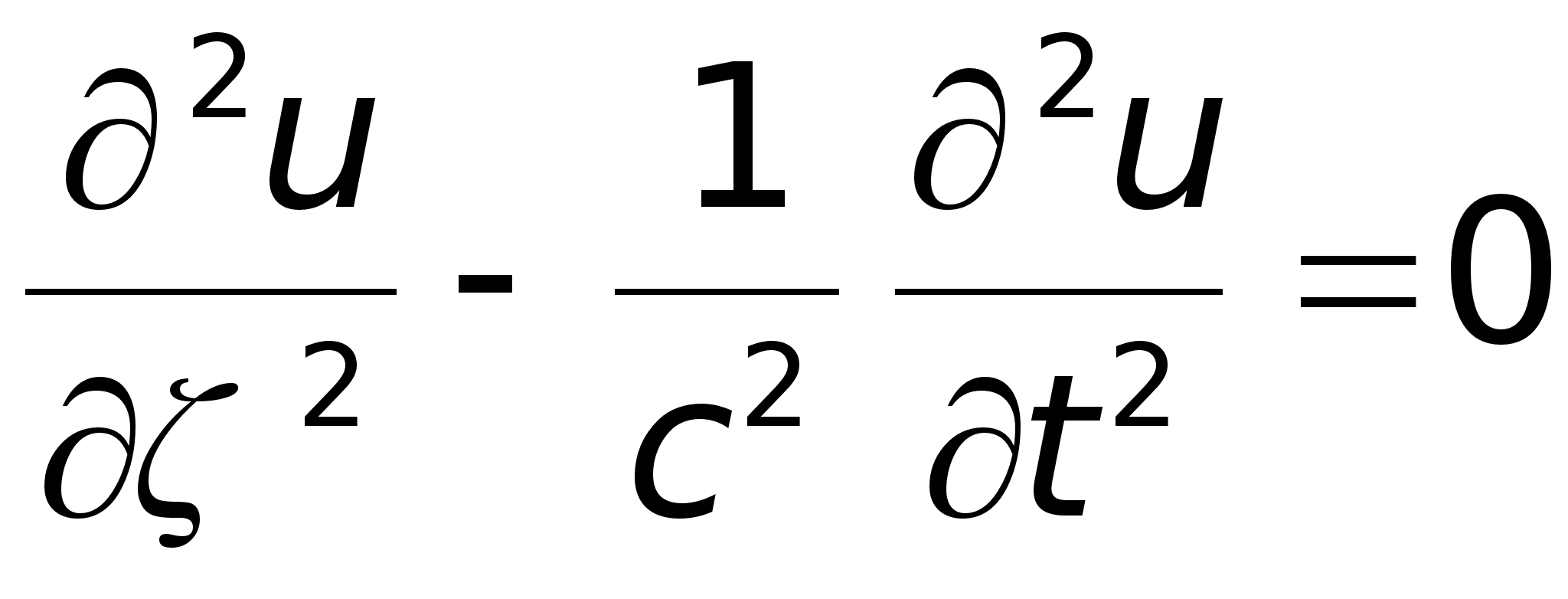 .
.
При этом
волновое число
связано с частотой
линейной зависимостью
![]() ,
или
,
или
![]() ,
где скорость
распространения
волны
,
где скорость
распространения
волны
![]() есть постоянная
величина. Однако
уже при учете
диссипативных
процессов
поведение волны
описывается
более сложными
уравнениями.
Закон дисперсии
есть постоянная
величина. Однако
уже при учете
диссипативных
процессов
поведение волны
описывается
более сложными
уравнениями.
Закон дисперсии
![]() также усложняется.
Для звуковых
волн в вязкой
теплопроводящей
среде и электромагнитных
волн в среде
с проводимостью
справедливы
следующие
соотношения
между волновым
числом и частотой:
также усложняется.
Для звуковых
волн в вязкой
теплопроводящей
среде и электромагнитных
волн в среде
с проводимостью
справедливы
следующие
соотношения
между волновым
числом и частотой:
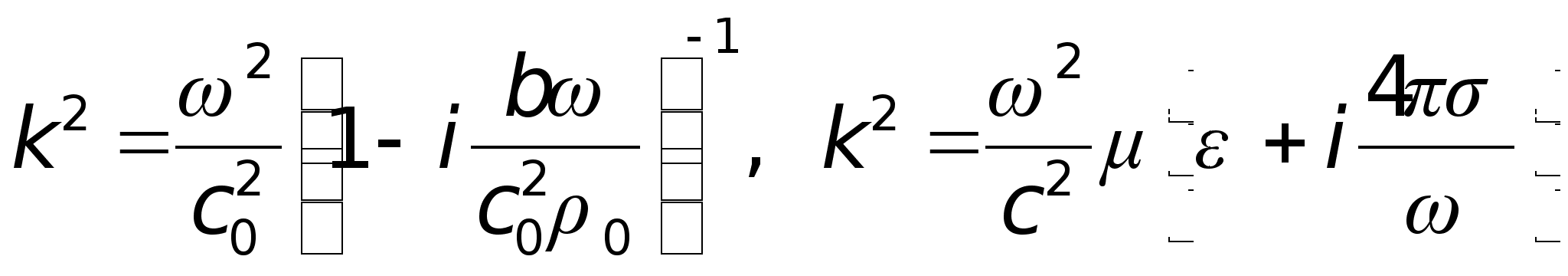 .
.
В более общих случаях от частоты могут сложным образом зависеть действительная и мнимая части волнового числа:
![]() .
.
Действительная
часть характеризует
зависимость
от частоты
фазовой скорости
распространения
волны
![]() ,
а мнимая часть
— зависимость
коэффициента
затухания волны
от частоты.
,
а мнимая часть
— зависимость
коэффициента
затухания волны
от частоты.
Во многих
случаях волновой
процесс удобно
описывать не
одним уравнением
типа волнового,
а системой
связанных
интегродифференциальных
уравнений
![]() .
Здесь
.
Здесь
![]() — матричный
оператор, действующий
на вектор-столбец
— матричный
оператор, действующий
на вектор-столбец
![]() .В
качестве
.В
качестве
![]() ,
например, для
акустических
волн может
служить совокупность
переменных
,
например, для
акустических
волн может
служить совокупность
переменных
![]() (колебательная
скорость, приращения
плотности,
давления,
температуры),
а для электромагнитных
волн — компоненты
векторов
напряженностей
электрического
и магнитного
полей, электрического
смещения и
магнитной
индукции. В
этом случае
формальная
схема отыскания
закона дисперсии
такова. Ищем
решение системы
в виде
(колебательная
скорость, приращения
плотности,
давления,
температуры),
а для электромагнитных
волн — компоненты
векторов
напряженностей
электрического
и магнитного
полей, электрического
смещения и
магнитной
индукции. В
этом случае
формальная
схема отыскания
закона дисперсии
такова. Ищем
решение системы
в виде
![]() :
:
![]() ,
,
Решение будет
нетривиальным,
только если
![]() .
Отсюда получаются
искомые зависимости
.
Отсюда получаются
искомые зависимости
![]() .
Наличие у
дисперсионного
уравнения
нескольких
корней
.
Наличие у
дисперсионного
уравнения
нескольких
корней
![]() означает, что
система может
описывать
несколько типов
собственных
волн (мод) среды.
означает, что
система может
описывать
несколько типов
собственных
волн (мод) среды.
Частотная дисперсия приводит к изменению закономерностей распространения немонохроматических волн. Действительно, различные спектральные компоненты обладают в диспергирующей среде отличающимися скоростями и коэффициентами затухания:
![]() .
.
В силу дисперсии
фазовой скорости
в процессе
распространения
изменяются
фазовые соотношения
между спектральными
компонентами.
Следовательно,
изменяется
результат их
интерференции:
форма немонохроматической
волны искажается.
Дисперсия
коэффициента
поглощения
![]() приводит к
трансформации
частотного
спектра волны
приводит к
трансформации
частотного
спектра волны
![]() и дополнительному
искажению формы
импульса.
и дополнительному
искажению формы
импульса.
§1. Материальные уравнения электромагнитного поля в среде с дисперсией.
Дисперсионные эффекты часто проявляются при распространении электромагнитных волн. Покажем, как видоизменяются исходные уравнения при учете этих свойств. Система уравнений Максвелла сохраняет свой вид. Свойства среды должны быть учтены в материальных уравнениях:
![]() .
.
Для статических и медленно изменяющихся полей можно написать
![]() ,
,
где
![]() — константы,
т. е. значения
— константы,
т. е. значения
![]() и
и
![]() в некоторой
точке среды
и в некоторый
момент времени
определяются
значениями
в некоторой
точке среды
и в некоторый
момент времени
определяются
значениями
![]() и
и
![]() в той же точке
и в тот же момент
времени.
в той же точке
и в тот же момент
времени.
При быстром изменении поля вследствие инерции внутренних движений и наличия пространственной микроструктуры среды наблюдается зависимость поляризации от поля, действующего в других точках и в другие моменты времени. При этом нужно иметь в виду, что в силу условия причинности поляризация и, следовательно, индукция зависят от полей, действовавших только в предыдущие моменты времени.
Сказанное можно записать математически, представляя материальные уравнения в общей интегральной форме:
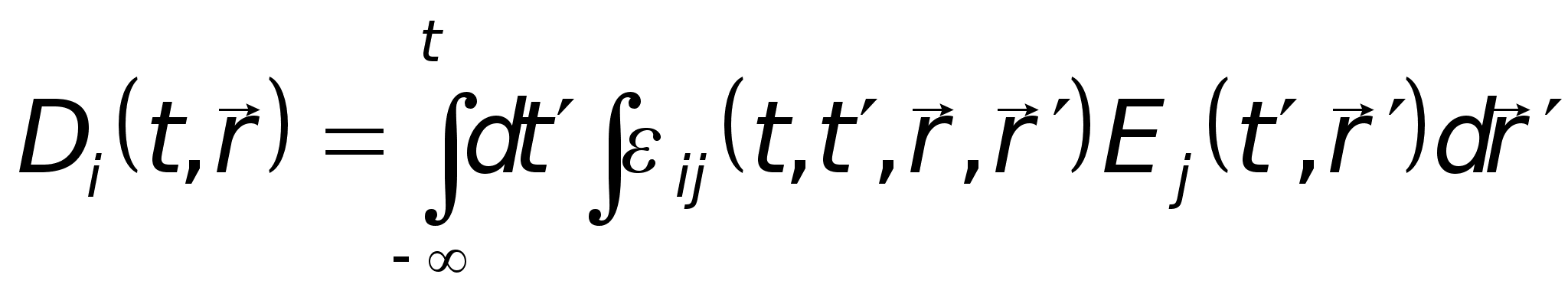 ,
(1.1)
,
(1.1)
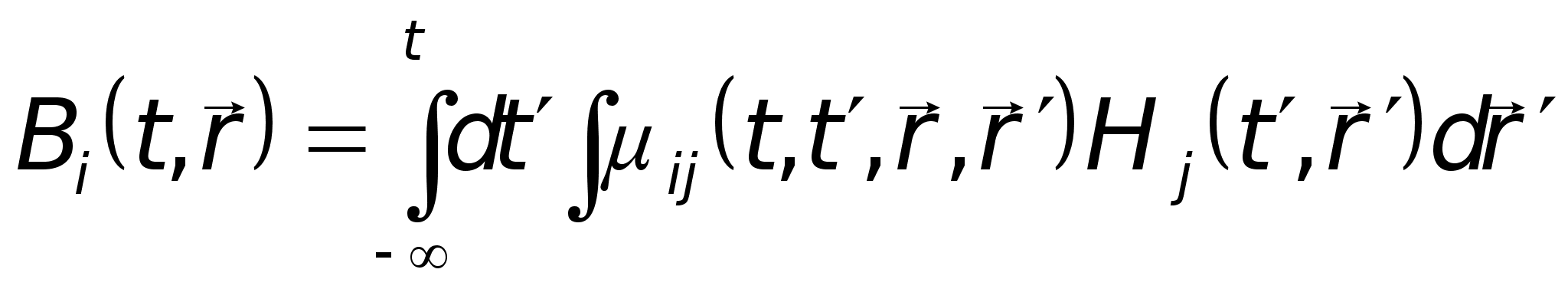 ,
(1.2)
,
(1.2)
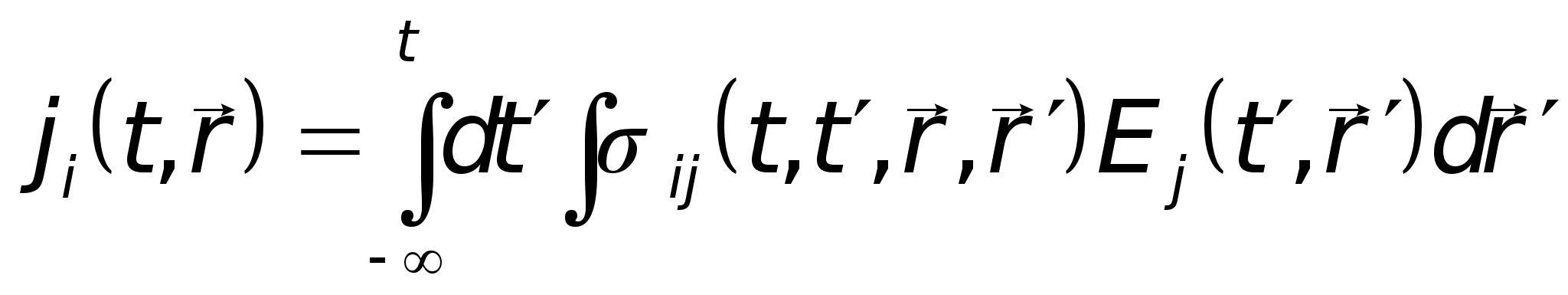 .
(1.3)
.
(1.3)
По дважды встречающимся индексам здесь и везде в дальнейшем предполагается суммирование.
Выражения (1.1) — (1.3) представляют собой наиболее общую функциональную форму записи материальных уравнений для линейной среды. В этой записи учтена возможность проявления нелокальности, запаздывания и анизотропных свойств среды.
В частном
случае, если
среда однородна
в пространстве
и не изменяет
со временем
своих свойств,
материальные
характеристики
![]() ,
,
![]() ,
,
![]() должны зависеть
лишь от разностей
координат
должны зависеть
лишь от разностей
координат
![]() и времени
и времени
![]() .
Тогда
.
Тогда
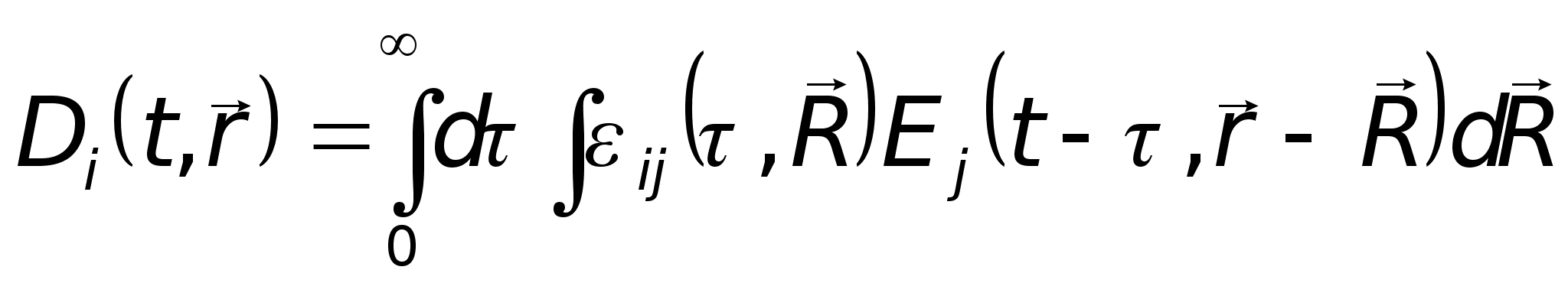 ,
(1.4)
,
(1.4)
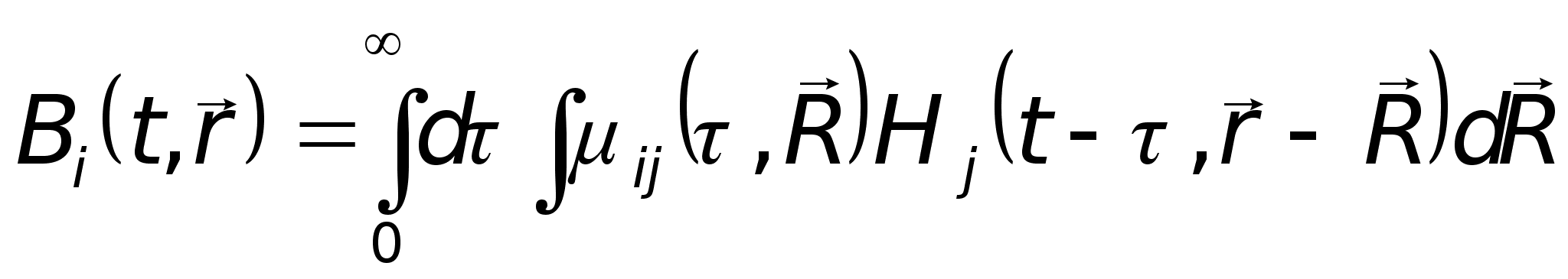 ,
(1.5)
,
(1.5)
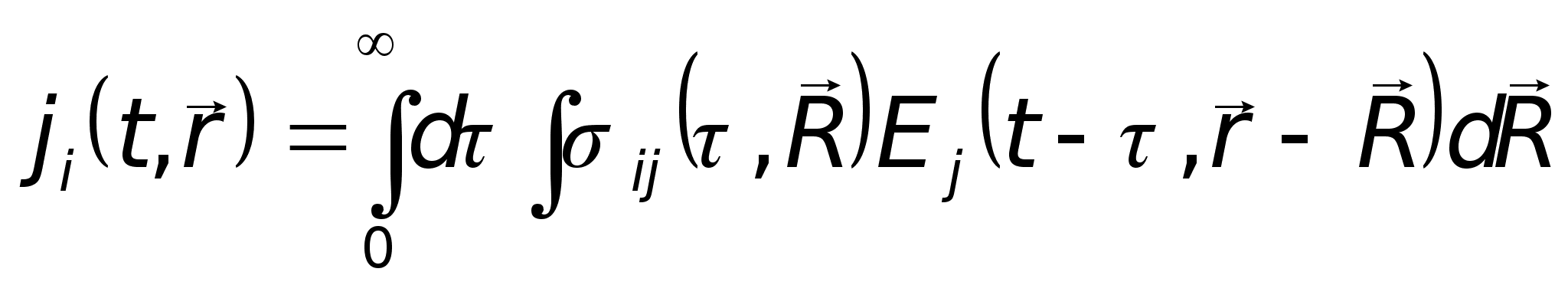 .
(1.6)
.
(1.6)
Связь между электрическим смещением и магнитной индукцией, полями и поляризациями среды определяется соотношениями
![]() .
(1.7)
.
(1.7)
Поэтому материальные уравнения можно записать также в виде
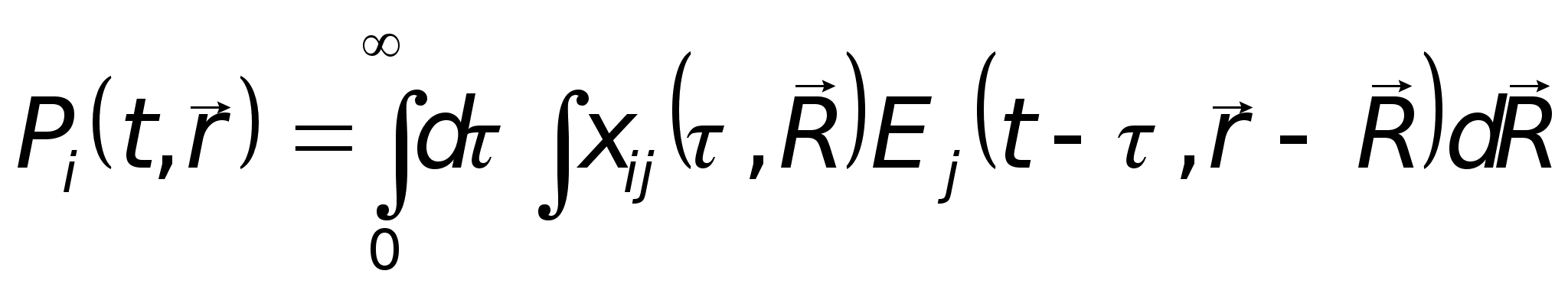 ,
(1.8)
,
(1.8)
где
![]() — тензор восприимчивости
среды. Аналогичное
выражение можно
записать для
— тензор восприимчивости
среды. Аналогичное
выражение можно
записать для
![]() .
.
Для проведения
дальнейшего
анализа удобно
разложить
![]() по плоским
волнам:
по плоским
волнам:
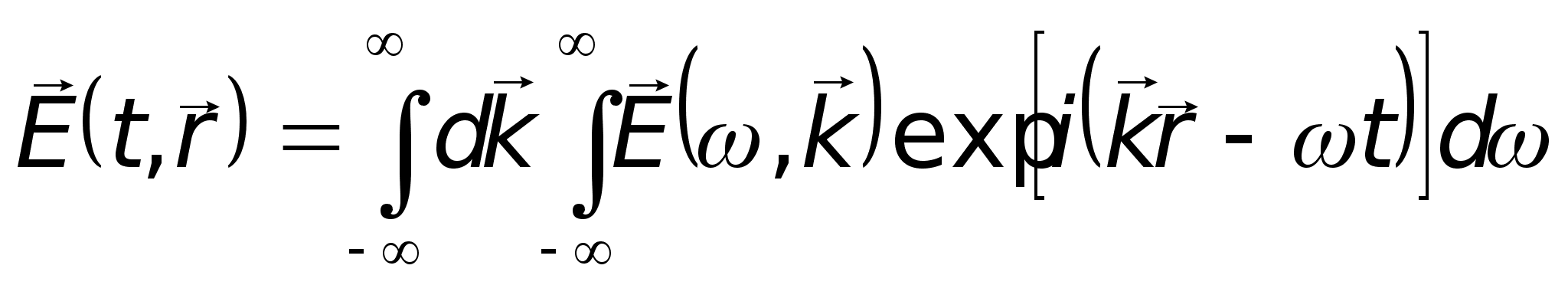 .
.
После обычного
перехода в
фурье-представление
в выражениях
для
![]() и
и
![]() получаем простую
зависимость
получаем простую
зависимость
![]() ,
(1.9)
,
(1.9)
![]() ,
(1.9)
,
(1.9)
где
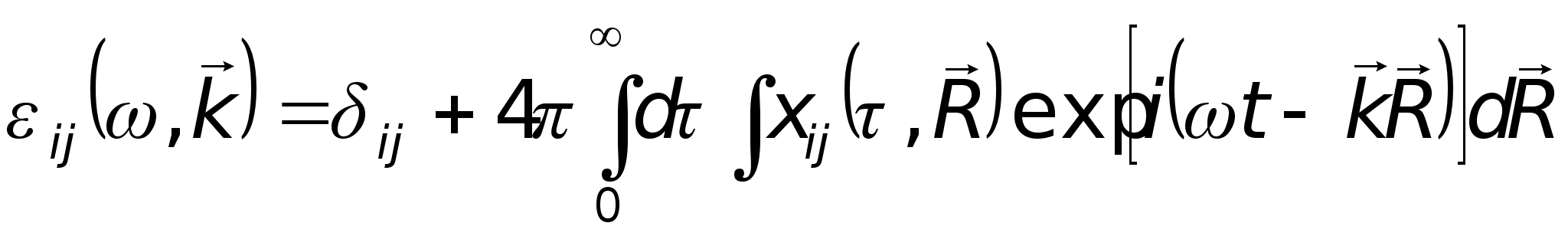 .
(1.10)
.
(1.10)
Видно, что компоненты тензора диэлектрической проницаемости зависят в общем случае от частоты и от волнового вектора волны.
Аналогичный
вывод можно
сделать для
магнитной
проницаемости
![]() и проводимости
и проводимости
![]() .
.
Таким образом,
дисперсия при
распространении
электромагнитных
волн может
проявляться
двояким образом
— как частотная
(за счет зависимости
![]() ,
,
![]() ,
,
![]() от частоты) и
как пространственная
(за счет зависимости
этих же параметров
от волнового
вектора
от частоты) и
как пространственная
(за счет зависимости
этих же параметров
от волнового
вектора
![]() ).
Частотная
дисперсия
существенна,
если частота
электромагнитных
волн близка
к собственным
частотам колебаний
в среде. Пространственная
же дисперсия
становится
заметной, когда
длина волны
сравнима с
некоторыми
характерными
размерами.
).
Частотная
дисперсия
существенна,
если частота
электромагнитных
волн близка
к собственным
частотам колебаний
в среде. Пространственная
же дисперсия
становится
заметной, когда
длина волны
сравнима с
некоторыми
характерными
размерами.
Для электромагнитных
волн в большинстве
случаев, даже
в оптическом
диапазоне,
характерный
размер
![]() (где
(где
![]() — длина волны
в среде:
— длина волны
в среде:
![]() )
и пространственной
дисперсией
можно пренебречь.
Однако в магнитоактивной
плазме существуют
области резонанса,
в которых
)
и пространственной
дисперсией
можно пренебречь.
Однако в магнитоактивной
плазме существуют
области резонанса,
в которых
![]() и параметр
и параметр
![]() становится
значительным
уже в радиодиапазоне.
Кроме того, при
полном пренебрежении
величинами,
содержащими
малое отношение
становится
значительным
уже в радиодиапазоне.
Кроме того, при
полном пренебрежении
величинами,
содержащими
малое отношение
![]() ,
не учитываются
некоторые
явления, возникающие
при распространении
электромагнитных
волн в различных
средах. Так,
учет пространственной
дисперсии в
плазме позволяет
объяснить
появление
бегущих плазменных
волн. Пространственная
дисперсия
является главной
причиной (а не
поправкой),
вызывающей
появление
естественной
оптической
активности
и оптической
анизотропии
кубических
кристаллов.
Если не интересоваться
этими специальными
случаями, то
при рассмотрении
частотной
дисперсии
пространственной
дисперсией
можно пренебречь.
,
не учитываются
некоторые
явления, возникающие
при распространении
электромагнитных
волн в различных
средах. Так,
учет пространственной
дисперсии в
плазме позволяет
объяснить
появление
бегущих плазменных
волн. Пространственная
дисперсия
является главной
причиной (а не
поправкой),
вызывающей
появление
естественной
оптической
активности
и оптической
анизотропии
кубических
кристаллов.
Если не интересоваться
этими специальными
случаями, то
при рассмотрении
частотной
дисперсии
пространственной
дисперсией
можно пренебречь.
При учете только частотной дисперсии материальное уравнение (1.9) имеет вид
![]() .
(1.11)
.
(1.11)
В отличие
от (1.9) здесь взяты
не компоненты
плоских волн
поля
![]() ,
а лишь временные
гармоники.
Диэлектрическая
проницаемость
,
а лишь временные
гармоники.
Диэлектрическая
проницаемость
![]() для волны с
частотой
для волны с
частотой
![]() — это тензор,
который в случае
изотропной
среды обращается
в скаляр:
— это тензор,
который в случае
изотропной
среды обращается
в скаляр:
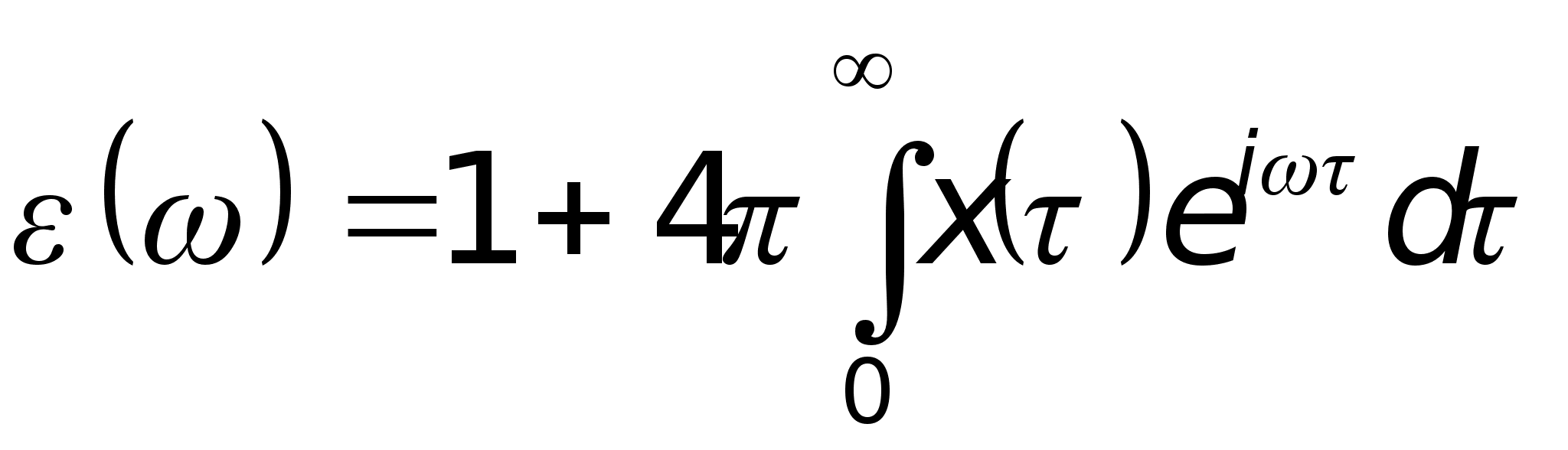 (1.12)
(1.12)
(напомним,
что
![]() — действительная
величина). Из
(1.12) следует, что
функция
— действительная
величина). Из
(1.12) следует, что
функция
![]() является комплексной:
является комплексной:
![]() ,
(1.13)
,
(1.13)
![]() ,
(1.14)
,
(1.14)
т.е.
![]() является четной
функцией, а
является четной
функцией, а
![]() — нечетной. Все
сказанное
справедливо
также для
— нечетной. Все
сказанное
справедливо
также для
![]() :
:
![]() .
(1.15)
.
(1.15)
Если в недиспергирующей среде диэлектрическая проницаемость — чисто реактивный параметр, а проводимость — чисто активный, то в среде с дисперсией это различие утрачивается. С увеличением частоты до значений, близких к собственным частотам среды, различие в свойствах диэлектриков и проводников постепенно исчезает. Так, наличие у среды мнимой части диэлектрической проницаемости с макроскопической точки зрения неотличимо от существования проводимости — и то и другое приводит к выделению тепла. Поэтому электрические свойства вещества можно характеризовать одной величиной — комплексной диэлектрической проницаемостью
![]() ,
(1.16)
,
(1.16)
где
![]() .
.
Можно установить
предельный
вид диэлектрической
проницаемости
при больших
частотах. В
пределе при
![]() имеем
имеем
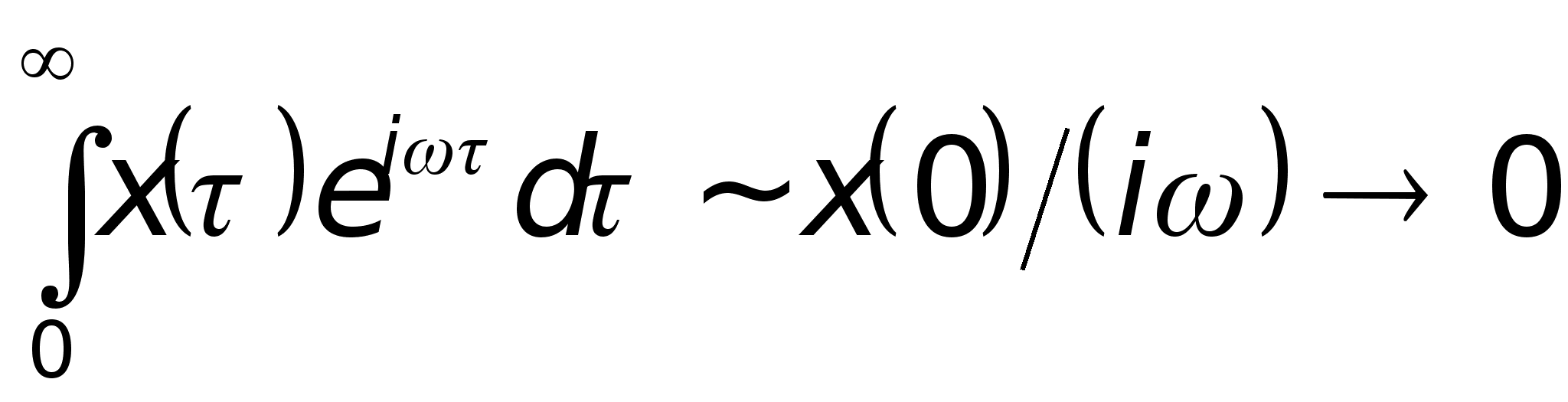 ,
,
и диэлектрическая
проницаемость
![]() ,
определяемая
выражениями
(1.6), (1.12), стремится
к единице при
,
определяемая
выражениями
(1.6), (1.12), стремится
к единице при
![]() .
.
Это же свойство
диэлектрической
проницаемости
следует и из
простого физического
рассмотрения.
При
![]() ,
когда частота
волны велика
по сравнению
с собственными
частотами
колебаний
электронов
в атомах вещества,
электроны можно
считать свободными.
Уравнение
движения свободного
электрона под
действием
гармонического
поля
,
когда частота
волны велика
по сравнению
с собственными
частотами
колебаний
электронов
в атомах вещества,
электроны можно
считать свободными.
Уравнение
движения свободного
электрона под
действием
гармонического
поля
![]() и решение этого
Уравнения имеют
вид
и решение этого
Уравнения имеют
вид
![]() .
.
Здесь
![]() — масса и заряд
электрона. Мы
не учитываем
силу, действующую
на заряд со
стороны магнитного
поля, так как
рассматривается
нерелятивистский
случай (
— масса и заряд
электрона. Мы
не учитываем
силу, действующую
на заряд со
стороны магнитного
поля, так как
рассматривается
нерелятивистский
случай (![]() ).
Поляризация
среды (дипольный
момент единицы
объема, содержащей
).
Поляризация
среды (дипольный
момент единицы
объема, содержащей
![]() электронов)
равна
электронов)
равна
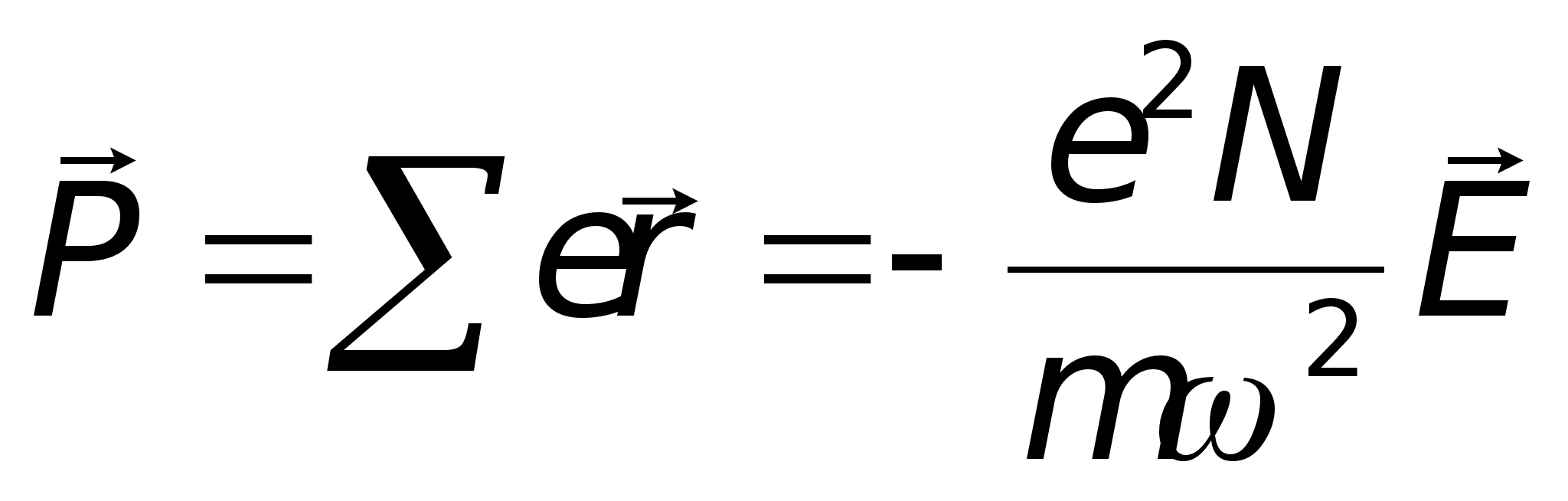 .
.
Отсюда
![]() и
и
![]() .
(1.17)
.
(1.17)
При
![]() мы получаем
из (1.17) прежний
результат:
мы получаем
из (1.17) прежний
результат:
![]() и
и
![]() .
Область применимости
формулы (1.17) для
сред, в которых
нет свободных
электронов,
лежит в диапазоне
далекой ультрафиолетовой
области для
самых легких
элементов.
.
Область применимости
формулы (1.17) для
сред, в которых
нет свободных
электронов,
лежит в диапазоне
далекой ультрафиолетовой
области для
самых легких
элементов.
С учетом (1.16) уравнения Максвелла для комплексных амплитуд примут вид
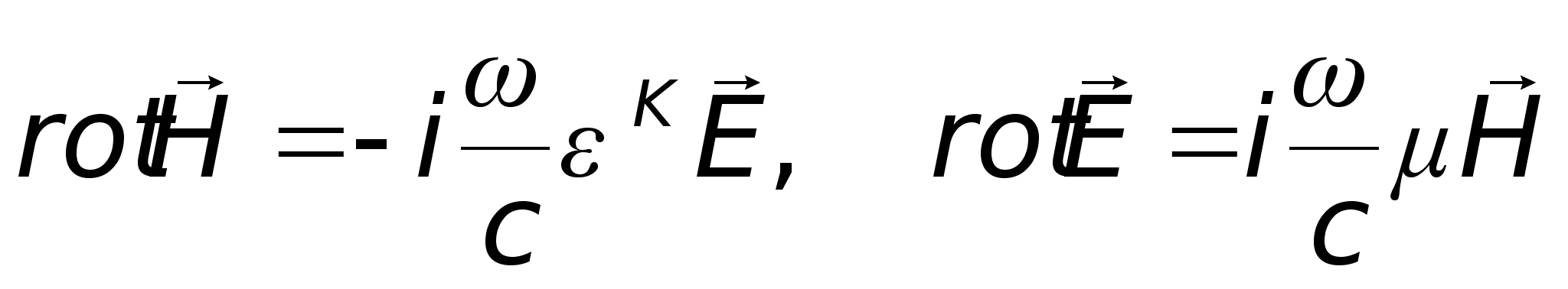 ,
(1.18)
,
(1.18)
![]() .
(1.18)
.
(1.18)
Поясним вывод
уравнения
![]() .
Из уравнения
непрерывности
при гармонической
зависимости
от времени
следует, что
.
Из уравнения
непрерывности
при гармонической
зависимости
от времени
следует, что
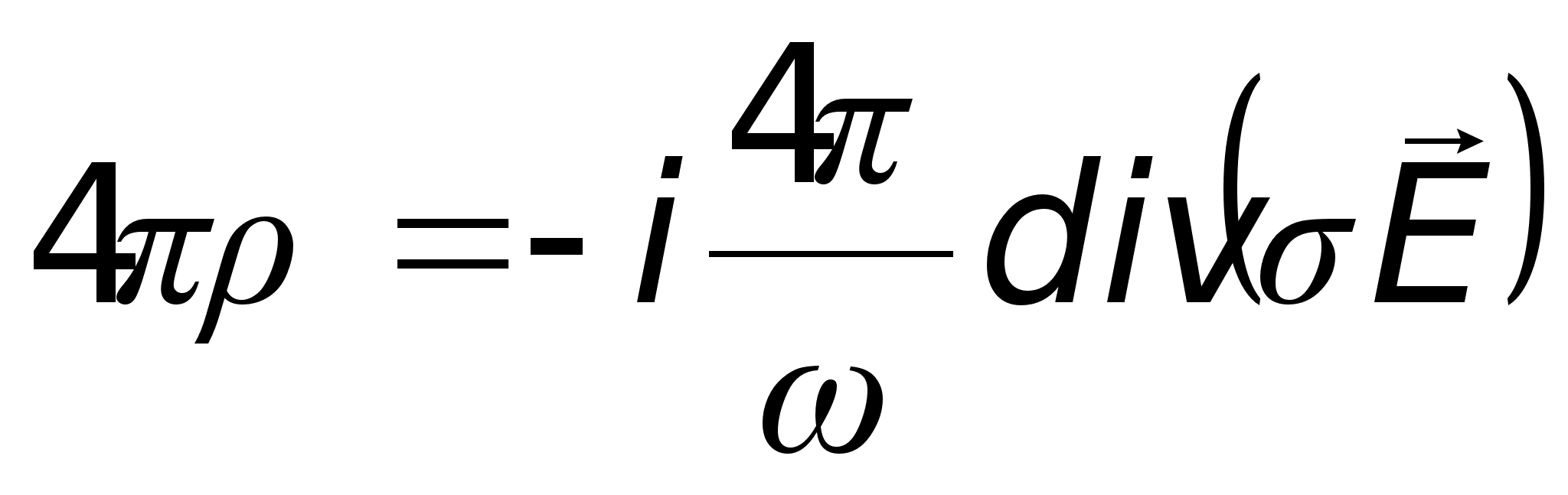 .
.
Подставляя
это соотношение
в уравнение
Максвелла
![]() ,
запишем его
в форме
,
запишем его
в форме
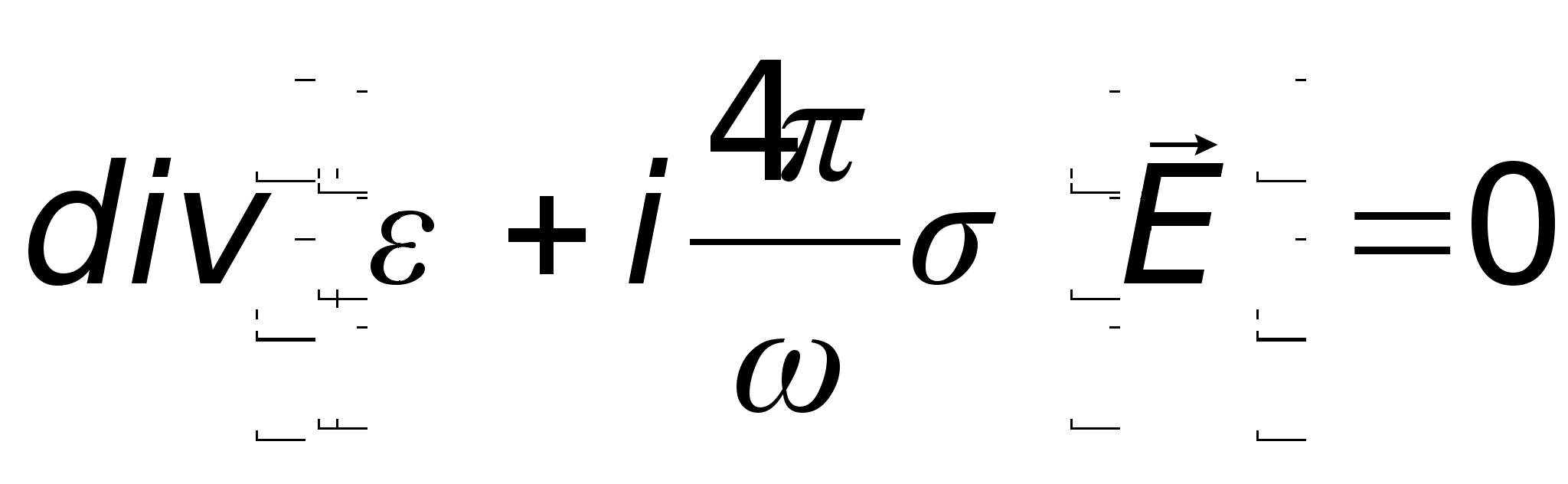 .
.
Учитывая
определение
![]() ,
получим уравнение
,
получим уравнение
![]() .
.
Таким образом, для высокочастотных монохроматических полей вместо диэлектрической проницаемости и проводимости удобно ввести комплексную диэлектрическую проницаемость, объединяющую оба эти понятия. Физически это означает, что ток в среде для высокочастотных полей нецелесообразно рассматривать как сумму тока проводимости и тока смещения. Вместо этого вводится полный ток
![]() ,
(1.19)
,
(1.19)
где
![]() — комплексный
вектор поляризации
среды.
— комплексный
вектор поляризации
среды.
§2. Закон дисперсии. Вектор объемной плотности поляризации.
Рассмотрим простые физические модели диспергирующих сред. Ясно, что простые модели, отражающие реальные свойства среды, могут быть построены в немногих случаях. Тем не менее они очень важны для понимания физики и заслуживают подробного обсуждения.
Для нахождения
зависимости
![]() от частоты
(закона дисперсии)
необходимо
решить задачу
о взаимодействии
электромагнитной
волны с имеющимися
в среде зарядами.
от частоты
(закона дисперсии)
необходимо
решить задачу
о взаимодействии
электромагнитной
волны с имеющимися
в среде зарядами.
Все современные теории дисперсии учитывают молекулярное строение вещества и рассматривают молекулы как динамические системы, обладающие собственными частотами. Молекулярные системы подчиняются законам квантовой механики. Однако результаты классической теории дисперсии во многих случаях приводят к качественно правильному выражению для показателей преломления и поглощения как функций частоты.
Диэлектрики
условно разделяются
на два типа —
неполярные
и полярные. В
молекулах
неполярных
диэлектриков
заряды электронов
точно компенсируют
заряды ядер,
причем центры
отрицательных
и положительных
зарядов совпадают.
В этом случае
в отсутствие
электромагнитного
поля молекулы
не обладают
дипольным
моментом. Под
действием поля
волны происходит
смещение электронов
(ионы при этом
можно считать
неподвижными,
поскольку их
масса велика
по сравнению
с массой электронов)
а каждая молекула
поляризуется
— приобретает
дипольный
момент
![]() .
Если диэлектрик
однороден и
в единице объема
содержится
.
Если диэлектрик
однороден и
в единице объема
содержится
![]() одинаковых
молекул, то
вектор объемной
плотности
поляризации
одинаковых
молекул, то
вектор объемной
плотности
поляризации
![]() .
.
Для определения
вектора
![]() необходимо
решить уравнение
движения электронов
в молекуле под
действием поля
волны и найти
смещение электронов
как функцию
поля. В классической
теории дисперсии
описание движения
электронов
в молекуле
основано на
модели Друде
— Лоренца, согласно
которой молекула
представляется
в виде одного
или нескольких
линейных
гармонических
осцилляторов,
соответствующих
нормальным
колебаниям
электронов
в молекуле.
Рассмотрим
уравнение
движения такого
осциллятора:
необходимо
решить уравнение
движения электронов
в молекуле под
действием поля
волны и найти
смещение электронов
как функцию
поля. В классической
теории дисперсии
описание движения
электронов
в молекуле
основано на
модели Друде
— Лоренца, согласно
которой молекула
представляется
в виде одного
или нескольких
линейных
гармонических
осцилляторов,
соответствующих
нормальным
колебаниям
электронов
в молекуле.
Рассмотрим
уравнение
движения такого
осциллятора:
![]() .
(2.1)
.
(2.1)
Здесь
![]() — эффективная
масса,
— эффективная
масса,
![]() — константа
затухания,
имеющая размерность
частоты,
— константа
затухания,
имеющая размерность
частоты,
![]() — резонансная
угловая частота
нормального
колебания,
— резонансная
угловая частота
нормального
колебания,
![]() — поле, действующее
на диполь. Для
плотных сред
действующее
поле
— поле, действующее
на диполь. Для
плотных сред
действующее
поле
![]() в однородном
диэлектрике
отличается
от среднего
макроскопического
поля в среде
на величину
в однородном
диэлектрике
отличается
от среднего
макроскопического
поля в среде
на величину
![]() и равно
и равно
![]() .
.
Отметим, что последнее равенство справедливо для изотропной среды и для кристаллов кубической симметрии.
При гармонической
зависимости
от времени поля
![]() из уравнения
(2.1) получим следующее
соотношение:
из уравнения
(2.1) получим следующее
соотношение:
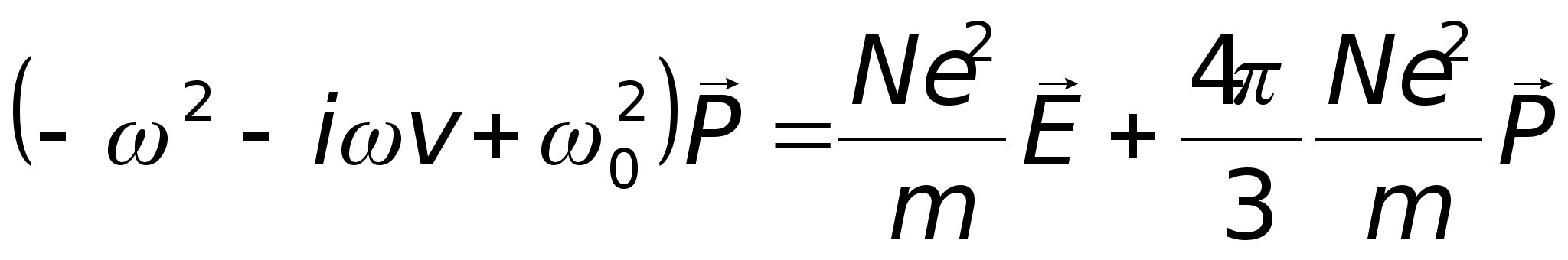 .
.
Отсюда удобно
выразить
![]() :
:
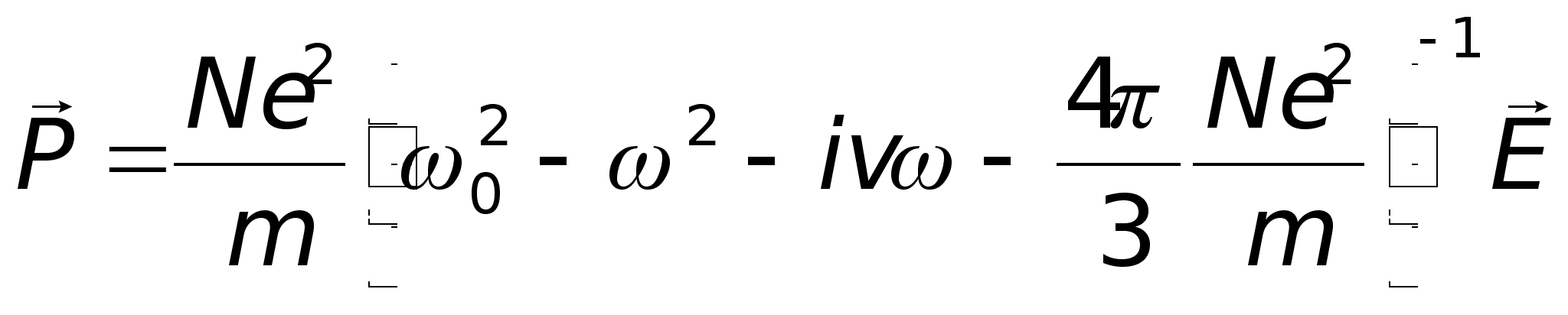 .
(2.2)
.
(2.2)
Учитывая,
что
![]() ,
из (2.2) найдем
,
из (2.2) найдем
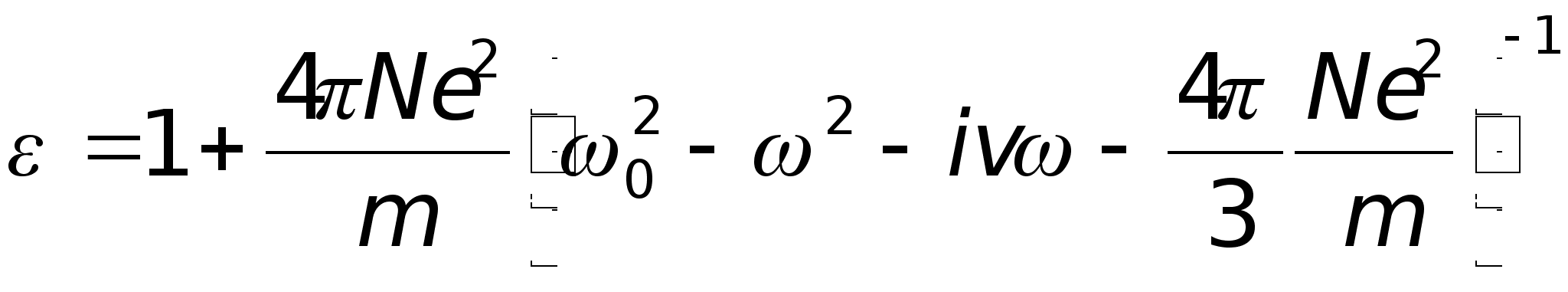 ,
(2.3)
,
(2.3)
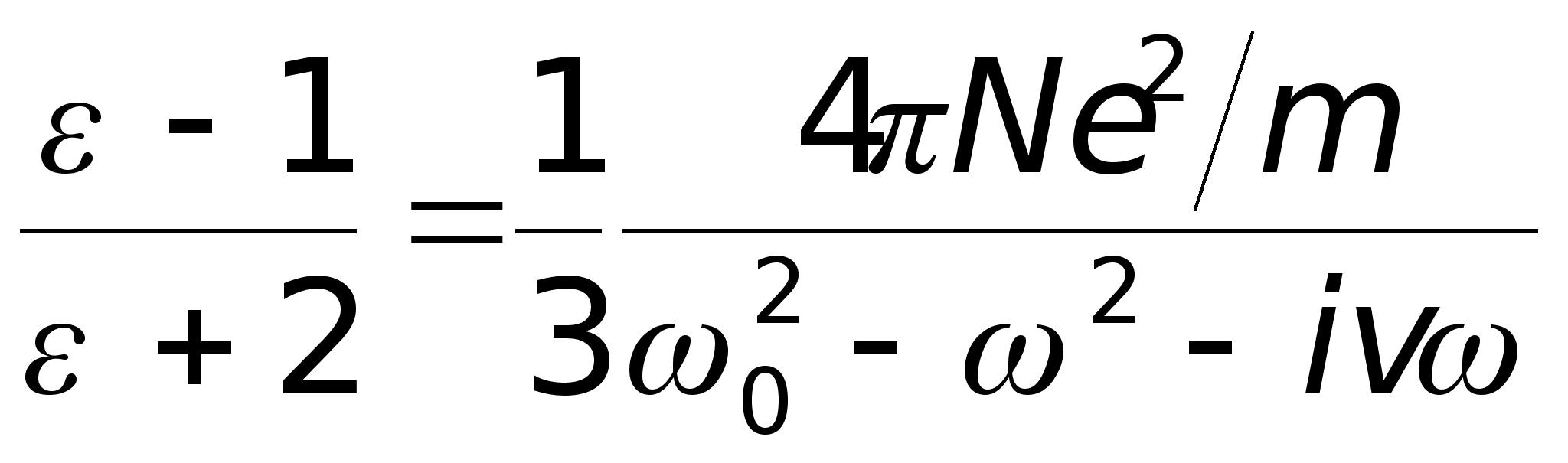 .
.
Разделяя в (2.3) действительную и мнимую части, получим
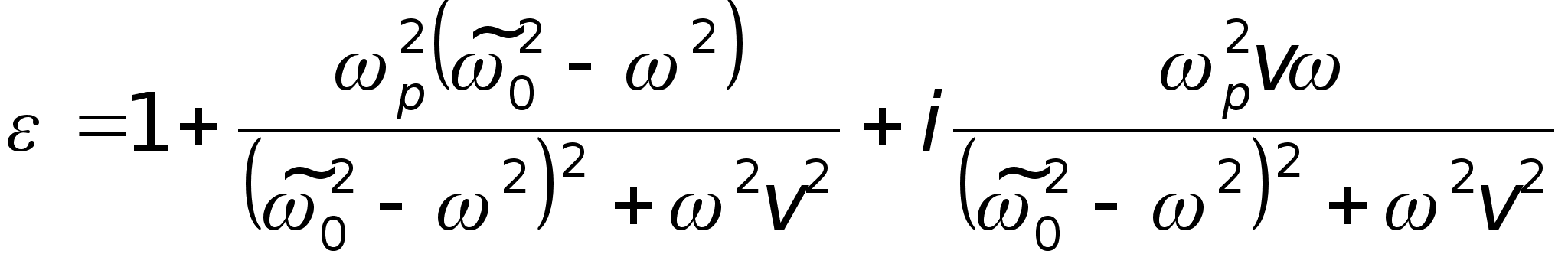 .
.
Здесь введены
обозначения
![]() ,
,
![]() .
В случае низких
частот, удовлетворяющих
условию
.
В случае низких
частот, удовлетворяющих
условию
![]() ,
придем к выражению
для статической
диэлектрической
проницаемости
,
придем к выражению
для статической
диэлектрической
проницаемости
![]() .
.
Для твердых
и жидких диэлектриков
![]() может значительно
превышать
единицу.
может значительно
превышать
единицу.
В газах плотность
поляризованных
молекул обычно
невелика. При
этом
![]() и можно считать,
что
и можно считать,
что
![]() мало отличается
от единицы.
Поэтому
мало отличается
от единицы.
Поэтому
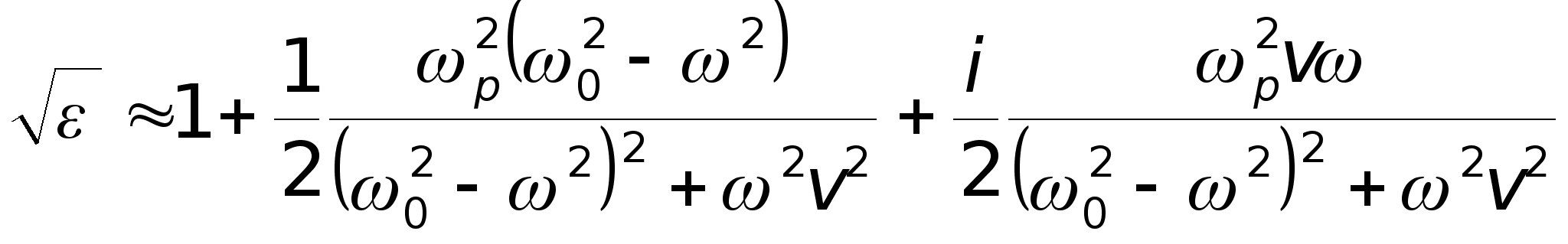 .
(2.4)
.
(2.4)
§3. Зависимость показателя преломления и поглощения от частоты.
Из (2.4) с учетом формул
![]()
для показателя преломления и поглощения получим
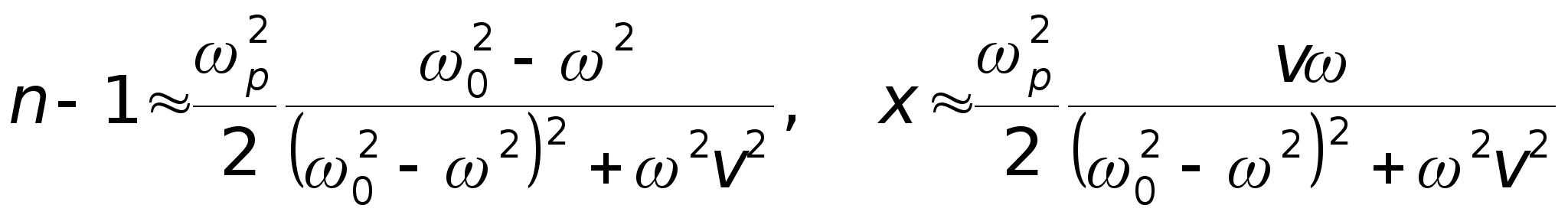 .
(3.1)
.
(3.1)
Выясним, как
зависят показатели
преломления
и поглощения
от частоты.
Если выполняется
условие
![]() ,
т. е. если частота
волны далека
от резонансной
(
,
т. е. если частота
волны далека
от резонансной
(![]() или
или
![]() ),
то
),
то
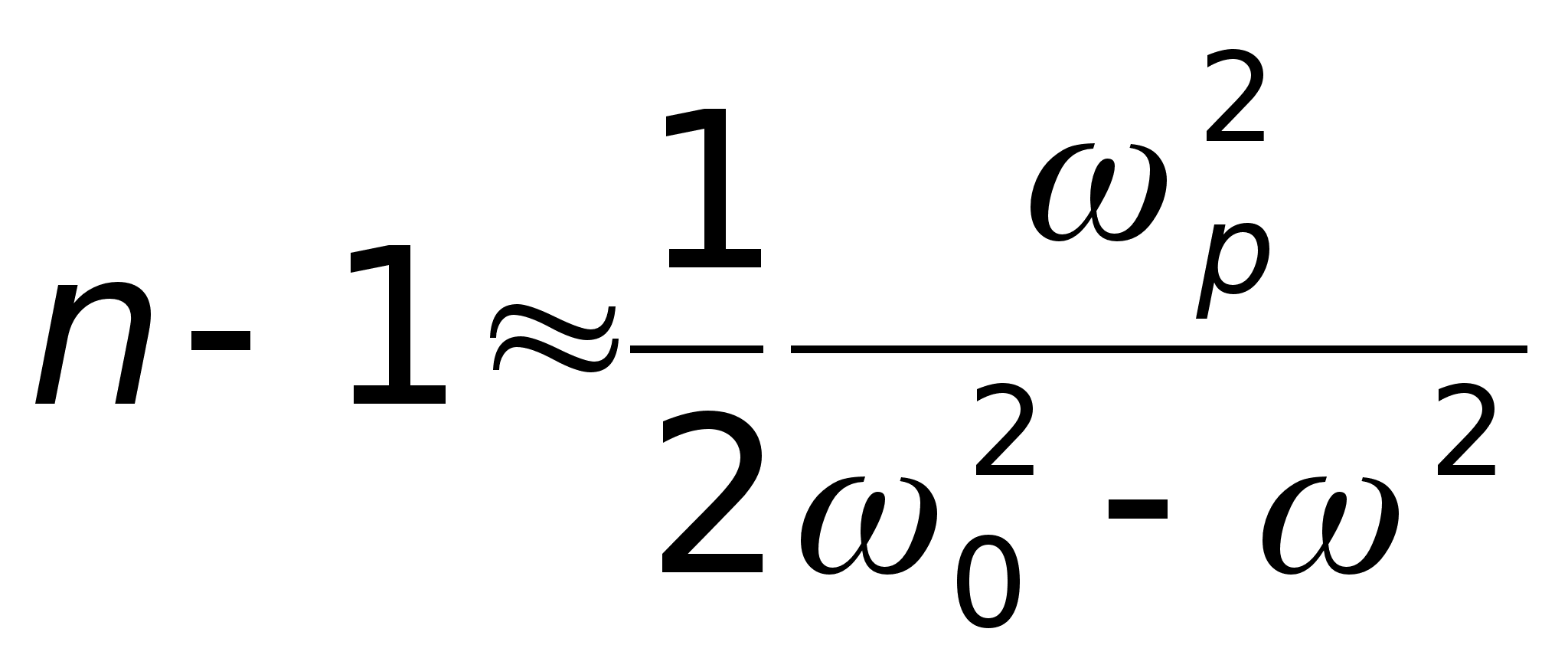 ,
(3.2)
,
(3.2)
т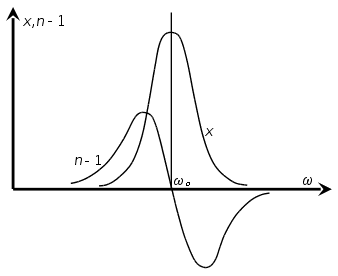
![]() .
е. показатель
преломления
мало отличается
от единицы. При
.
е. показатель
преломления
мало отличается
от единицы. При
![]() ,
величина
,
величина
![]() ;
она увеличивается
с ростом частоты.
При
;
она увеличивается
с ростом частоты.
При
![]() значение
значение
![]() отрицательное;
отрицательное;
![]() также увеличивается
с ростом
также увеличивается
с ростом
![]() ,
приближаясь
к единице (рис.
1). Показатель
поглощения
,
приближаясь
к единице (рис.
1). Показатель
поглощения
![]() в этом диапазоне
частот мал.
Вблизи резонанса
в этом диапазоне
частот мал.
Вблизи резонанса
![]() показатель
преломления
уменьшается
с ростом частоты.
При условии
точного резонанса,
когда
показатель
преломления
уменьшается
с ростом частоты.
При условии
точного резонанса,
когда
![]() ,
,
![]() обращается
в единицу, а
показатель
поглощения
принимает
максимальное
значение. Область
частот, в которой
показатель
преломления
убывает с увеличением
частоты, называется
областью аномальной
дисперсии;
здесь имеет
место возрастание
фазовой скорости.
обращается
в единицу, а
показатель
поглощения
принимает
максимальное
значение. Область
частот, в которой
показатель
преломления
убывает с увеличением
частоты, называется
областью аномальной
дисперсии;
здесь имеет
место возрастание
фазовой скорости.
В случае, когда молекула моделируется совокупностью осцилляторов различных типов, обладающих разными резонансными частотами, для диэлектрической проницаемости можно получить выражение, обобщающее (2.3):
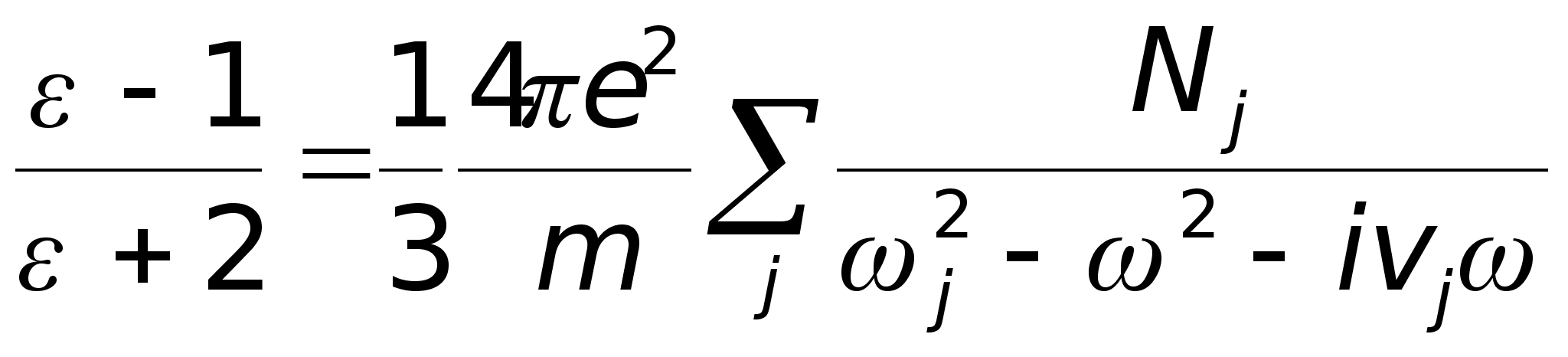 .
(3.3)
.
(3.3)
Здесь
![]() — объемная
плотность числа
осцилляторов
с частотой
— объемная
плотность числа
осцилляторов
с частотой
![]() .
.
Если вычислить
дипольный
момент единицы
объема, пользуясь
методами квантовой
механики, то
для
![]() получается
формула, аналогичная
(3.3), с той лишь
разницей, что
получается
формула, аналогичная
(3.3), с той лишь
разницей, что
![]() заменяется
в ней на
заменяется
в ней на
![]() ,
где
,
где
![]() — сила осциллятора
для перехода
с частотой
— сила осциллятора
для перехода
с частотой
![]() .
Суммирование
ведется по всем
разрешенным
дипольным
переходам.
.
Суммирование
ведется по всем
разрешенным
дипольным
переходам.
Формулы (2.3) и (3.3) получены для модели независимых атомов, однако они дают вполне правильное феноменологическое описание любой системы, спектр поглощения которой представляет набор дискретных линий.
Мы обсудили модель, дающую закон дисперсии для диэлектриков, молекулы которых приобретают дипольный момент только во внешнем поле. Но молекулы полярных диэлектриков (например, воды) обладают дипольным моментом и в отсутствие поля. Механизм поляризации такого диэлектрика сводится к ориентирующему действию поля волны.
Пусть дипольный
момент одной
молекулы равен
![]() .
При отсутствии
волны векторы
.
При отсутствии
волны векторы
![]() из-за теплового
движения
ориентированы
хаотически.
Если же в среде
распространяется
волна, каждый
элементарный
диполь приобретает
составляющую,
параллельную
вектору
из-за теплового
движения
ориентированы
хаотически.
Если же в среде
распространяется
волна, каждый
элементарный
диполь приобретает
составляющую,
параллельную
вектору
![]() .
Следовательно,
становится
отличным от
нуля дипольный
момент
.
Следовательно,
становится
отличным от
нуля дипольный
момент
![]() единицы объема:
единицы объема:
![]() .
(3.4)
.
(3.4)
В этом выражении
![]() — угол между
векторами
— угол между
векторами
![]() и
и
![]() — случайный
параметр; угловые
скобки обозначают
усреднение
по ансамблю
молекул. Для
вычисления
— случайный
параметр; угловые
скобки обозначают
усреднение
по ансамблю
молекул. Для
вычисления
![]() воспользуемся
статистическим
законом распределения
Больцмана
воспользуемся
статистическим
законом распределения
Больцмана
![]() .
.
Здесь
![]() — потенциальная
энергия молекулы
в электрическом
поле;
— потенциальная
энергия молекулы
в электрическом
поле;
![]() эрг/К — постоянная
Больцмана;
эрг/К — постоянная
Больцмана;
![]() — константа,
определяемая
условием нормировки
— константа,
определяемая
условием нормировки
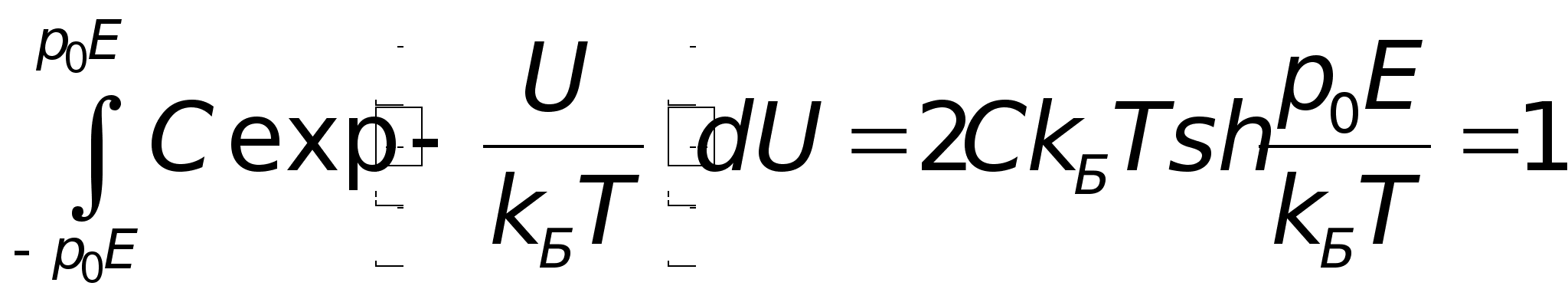 .
(3.5)
.
(3.5)
Мы не будем
интересоваться
здесь нелинейными
эффектами,
поэтому считаем
энергию ориентации
малой по сравнению
с энергией
теплового
движения:
![]() .
В этом приближении
из (3.5) имеем
.
В этом приближении
из (3.5) имеем
![]() .
Проводя усреднение
в формуле (3.4),
получим
.
Проводя усреднение
в формуле (3.4),
получим
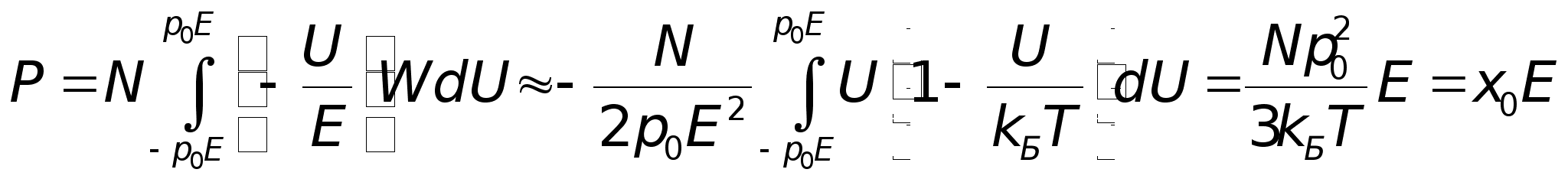 .
(3.6)
.
(3.6)
Если
![]() ,
то в разложении
,
то в разложении
![]() в ряд по степеням
в ряд по степеням
![]() появятся нелинейные
члены.
появятся нелинейные
члены.
До сих пор предполагалось, что переориентация диполей мгновенно следует за изменениями поля электромагнитной волны. На самом же деле имеется запаздывание, учет которого позволяет описать эффекты частотной дисперсии при распространении сигнала в среде с хаотически ориентированными дипольными молекулами.
Считаем,
следуя Дебаю,
что при включении
в момент
![]() поля волны
поля волны
![]() поляризация
в данной точке
пространства
изменяется
по закону
поляризация
в данной точке
пространства
изменяется
по закону
![]() .
(3.7)
.
(3.7)
Здесь
![]() — статическая
(при
— статическая
(при
![]() )
восприимчивость.
При учете только
частотной
дисперсии для
изотропной
среды из формулы
(1.8) получаем
)
восприимчивость.
При учете только
частотной
дисперсии для
изотропной
среды из формулы
(1.8) получаем
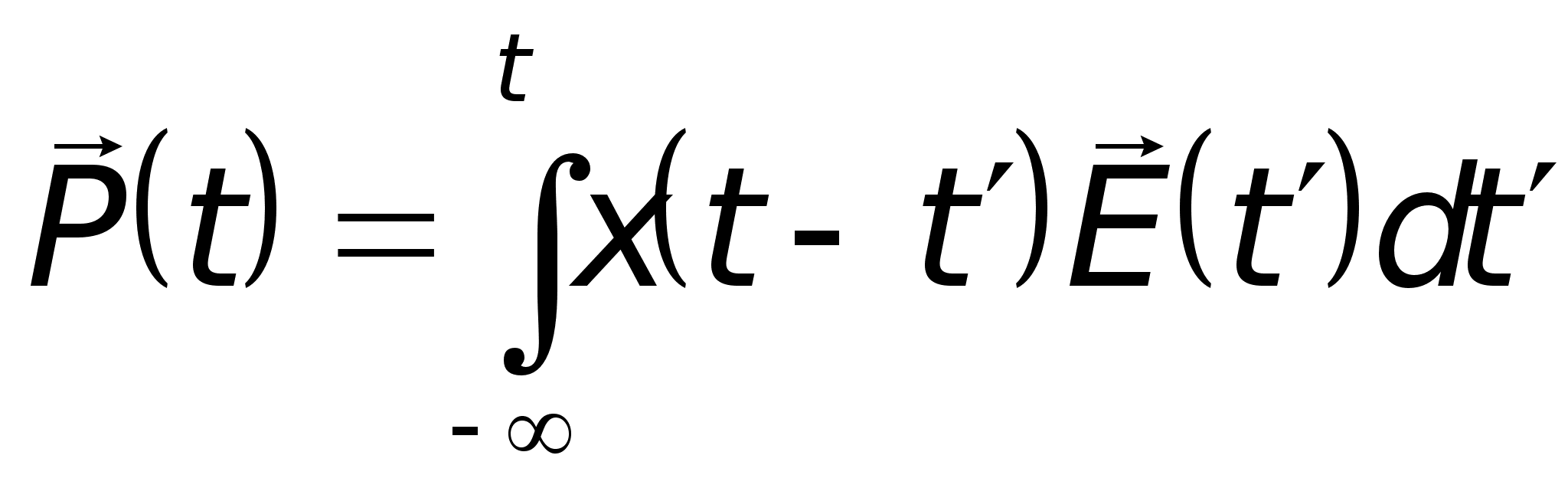 .
(3.8)
.
(3.8)
Как нетрудно проверить, зависимость (3.7) следует из (3.8) при
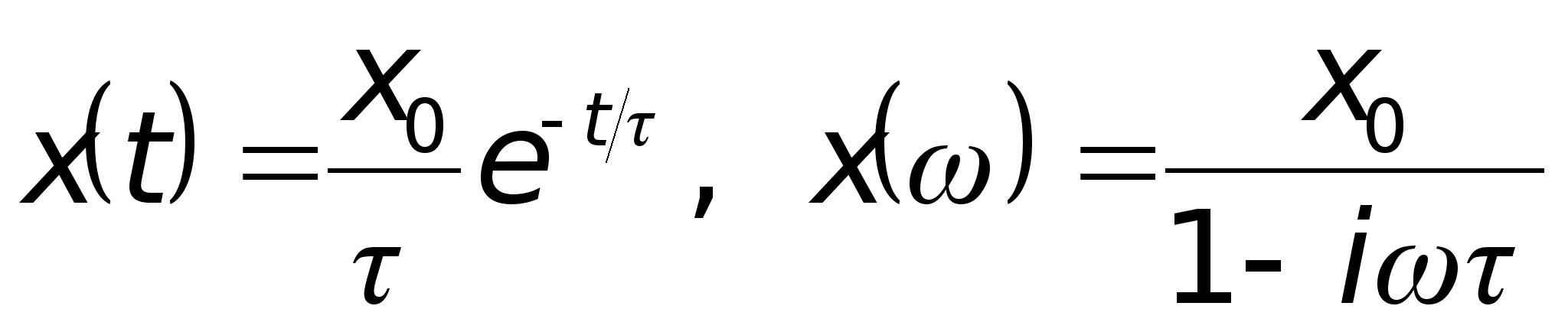 .
(3.9)
.
(3.9)
Следовательно,
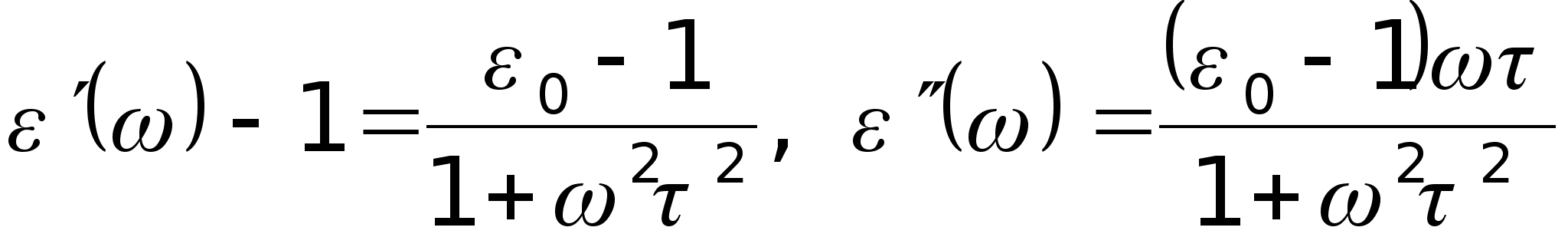 ,
(3.10)
,
(3.10)
где
![]() — статическая
диэлектрическая
проницаемость.
Функция
— статическая
диэлектрическая
проницаемость.
Функция
![]() ,
а значит, и потери
энергии имеют
максимум при
,
а значит, и потери
энергии имеют
максимум при
![]() .
Время релаксации
.
Время релаксации
![]() ,
например, в
парах воды
имеет порядок
,
например, в
парах воды
имеет порядок
![]() ,
и «резонансное»
поглощение
возможно в
миллиметровом
диапазоне
электромагнитных
волн.
,
и «резонансное»
поглощение
возможно в
миллиметровом
диапазоне
электромагнитных
волн.
При
![]() дисперсия
(3.10)
несущественна.
Так, при распространении
волн сантиметрового
диапазона и
более длинных
в тропосфере,
представляющей
собой смесь
молекул воздуха
(кислород, азот
и т. д.) и паров
воды, можно
пользоваться
формулой
дисперсия
(3.10)
несущественна.
Так, при распространении
волн сантиметрового
диапазона и
более длинных
в тропосфере,
представляющей
собой смесь
молекул воздуха
(кислород, азот
и т. д.) и паров
воды, можно
пользоваться
формулой
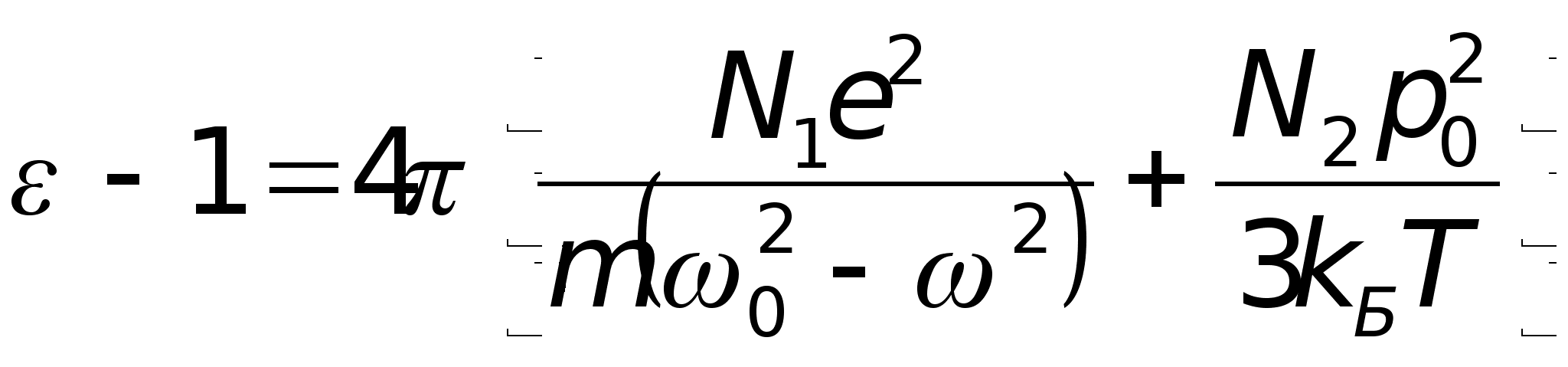 .
(3.11)
.
(3.11)
Здесь
![]() — объемные
концентрации
молекул воздуха
и пара. Принято,
что поле в среде
равно полю
волны, и соударениями
можно пренебречь.
Собственные
частоты молекул
газов, входящих
в состав воздуха,
лежат в области
— объемные
концентрации
молекул воздуха
и пара. Принято,
что поле в среде
равно полю
волны, и соударениями
можно пренебречь.
Собственные
частоты молекул
газов, входящих
в состав воздуха,
лежат в области
![]() >15
ГГц (
>15
ГГц (![]() см). Поэтому в
(3.11)
для
см). Поэтому в
(3.11)
для
![]() см
см
![]() .
Однако в оптическом
и миллиметровом
диапазонах
имеются области
резонансного
поглощения
волн. Поэтому
для целей радиосвязи
в тропосфере
в этом диапазоне
необходимо
выбирать «окна
прозрачности»,
т. е. пользоваться
частотами, не
совпадающими
с собственными
частотами
среды.
.
Однако в оптическом
и миллиметровом
диапазонах
имеются области
резонансного
поглощения
волн. Поэтому
для целей радиосвязи
в тропосфере
в этом диапазоне
необходимо
выбирать «окна
прозрачности»,
т. е. пользоваться
частотами, не
совпадающими
с собственными
частотами
среды.
Заключение.
Подводя итоги,
следует отметить,
что дисперсию
электромагнитных
волн можно
условно разделить
на частотную
(за счет зависимости
![]() ,
,
![]() ,
,
![]() от частоты) и
пространственную
(за счет зависимости
этих же параметров
от волнового
вектора
от частоты) и
пространственную
(за счет зависимости
этих же параметров
от волнового
вектора
![]() ).
Как уже говорилось,
частотная
дисперсия
существенна,
если частота
электромагнитных
волн близка
к собственным
частотам колебаний
в среде. Пространственная
же дисперсия
становится
заметной, когда
длина волны
сравнима с
некоторыми
характерными
размерами.
).
Как уже говорилось,
частотная
дисперсия
существенна,
если частота
электромагнитных
волн близка
к собственным
частотам колебаний
в среде. Пространственная
же дисперсия
становится
заметной, когда
длина волны
сравнима с
некоторыми
характерными
размерами.
При использовании диэлектриков в переменных электромагнитных полях необходимо знать собственные частоты колебаний молекул вещества диэлектрика для установления характера зависимости показателя преломления и поглощения (и других параметров) от частоты и во избежание (если это необходимо) резонансного поглощения электромагнитных волн.
Характерной особенностью диэлектриков является необходимость отдельного рассмотрения явления дисперсии для полярных и неполярных молекул, что обусловлено наличием (отсутствием) дипольного момента в отсутствии внешнего электромагнитного поля у полярных (неполярных) диэлектриков.
Литература.
Виноградова М. Б., Руденко О. В., Сухоруков А. П. «Теория волн». Москва «Наука», 1990 г.
15

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ им. В.Н.КАРАЗИНА
Курсовая работа на тему:
“Исследование явления дисперсии электромагнитных волн в диэлектриках”.
Выполнил: студент 3 курса ХНУ
Радиофизического
факультета группы РР-33
Зинченко Д. И.
Преподаватель: Богатская О. В.
Харьков 2003