Реферат: Универсальная геометрия в природе и архитектуре

Реферат: Универсальная геометрия в природе и архитектуре

“Геометрия владеет двумя сокровищами: одно из них - это

теорема Пифагора, и другое – деление отрезка в среднем и

крайнем отношении…Первое можно сравнить с мерой

золота, второе больше напоминает драгоценный камень”

Иоганн Кеплер

(Н.Васютинский. Золотая пропорция.-М.:Молодая

гвардия,1990,с.8)

Теория архитектурных пропорций развивалась не только как профессионально-эстетическое отражение практики, но и как процесс адаптации к архитектурным задачам представлений о геометрии и законах пространства, полученных в других областях знания (физика, философия, биология, психология и т.д.). В рамках профессиональной практики, эмпирическое познание законов гармонии осуществлялось через диалектическое отражение единства и противоположности модульных и геометрических систем пропорций.

Ориентация на необходимость гармонизации формы всегда опиралась на объективность избирательного подхода человека при восприятии пространства (т.е. на предположение о существовании в природе и механизмах восприятия особенных отношений, соответствующих живой материи, а в отдельных древних гипотезах – и природе всего космоса). Это утверждало гармонию как законную норму, как порядок отношений в геометрии объекта искусственной природы, соответствующий законам естественной природы. С древности, мерой архитектурных объектов выступал человек. Позже, под давлением социальных требований унификации и стандартизации, антропометрические системы измерения сменились абстрактными численными и линейными мерами.

Эмпирический поход получил импульс в развитии в связи с бурным ростом капиталистической промышленности (резко возросшие объемы и скорость строительства, новые технологии). Но утвердить в социальной практике право человека на эстетику и гармонию, в противовес элементарной модульной системе (кубической решетке, основанной на механическом членении пространства на абстрактные доли - метры, сантиметры и миллиметры), ему не удалось.

К середине ХХ в. эмпирический подход, не смог отстоять свою состоятельность и исчерпал себя. К этому времени на базе традиционной геометрии были отработаны различные методы пропорционирования. Но в условиях массового индустриального строительства, осуществляемого анонимными заказчиками архитектуры, их применение было крайне ограничено. Одновременно, на уровне идей и концепций, были выработаны новые подходы к нормативному обоснованию объективности пространственной гармонии.

Серьезный шаг в этом направлении сделал Цейзинг (середина ХIХ века), установивший связи пропорций тела человека с отношениями “золотого сечения” (числами Фибоначчи) и возродившей антропоцентрическую идею в архитектурной метрологии (3). Спустя почти столетие, Ле Корбюзье реализовал идею Цейзинга в “Модулоре” - модульной системе для строительства, которая соответствовала статическим и динамическим пропорциям человека (7).

Расширился перечень прикладных математических средств архитектурной пропорции: векторный анализ в приложении к природным формам (20), модели геометрического кодирования зрительной информации, так называемые коды размерно-пространственных структур (19), применение систем уравнений (теорема Пифагора и отношения среднепропорционального), как механизма выделения приоритетных отношений и конструирования особых, архитектурных, модульно-геометрических (3,4,5,6) пространственных образований.

1.2 Зрительное восприятие и геометрия. Принцип соответствия пропорций архитектуры и человека, находит свое дальнейшее развитие на более тонком уровне отражения пространства человеком, в механизмах зрительного восприятия. Он связывается с законом Вебера-Фехнера (9,12): процесс отражения пространственной информации зрительной системой связан с логарифмическими механизмами восприятия, преобразования, коммуникации и представления ее в зрительной коре. Иначе, сетчатка логарифмирует изображенные на ней проекции объектов, превращая действительные пространственные величины в частоты колебаний нейронов. Степени возбуждения, или пространственные частоты, пройдя длинный путь, передают степень возбуждения в мозг, и возбужденная зрительная кора воспроизводит образ объекта восприятия, превращая степени, в обратном порядке, в действительные отношения. Это уже специфическая оптика, реализуемая на уровне прямых и обратных связей нервной деятельности и поддержанная электрическими и химическими процессами. Не удивительно, что с логарифмическими механизмами восприятия зрительной информации естественно связываются отношения “золотого сечения”, сочетающего в себе, как арифметическую, так и геометрическую прогрессии, и обладающего универсальными логарифмическими особенностями (9).

С позиций современного знания о зрительном восприятии, предположения древних ученых и философов (Пифагорейская школа, Эмпедокл, Евклид) о том, что глаза испускают особые лучи во внешнее пространство, благодаря чему человек видит (Л.В.Тарасов, А.Н.Тарасова, Беседы о преломлении света, - М.: Наука, 1982 г. с.123), сегодня представляются не такими уж и наивными. Они правильно отражают принцип зрения, с тем уточнением, что мозг действительно испускает “лучи”, но не во внешнее пространство, а на сетчатку, и производит локацию пространственной геометрии внешнего пространства, но представленной в проекциях на сетчатке оптической системой глазного яблока.

Во второй половине ХХ века появляются информационные подходы (приложение закона Клода Шеннона о количественной мере информации к исследованию архитектурных пропорций), согласующиеся с законом Вебера-Фехнера и обосновывающие логарифмические принципы отражения пространства (13), но уже с позиций теории информации. Современное естествознание так же подтверждает логарифмическую природу физических явлений (например, периодичность, длительность). В частности, согласно второму началу термодинамики (закону энтропии), естественная природа теряет упорядоченность по логарифмической зависимости (11,21,24), т.е. процесс распада вещества периодически связан с его количеством (массой) в логарифмической форме.

Заметное расширение естественнонаучного начала в познании архитектурных пропорций характеризует не только кризис эмпирического познания, но и стремление к большей объективации знания, выходящее за рамки исследований возможностей абстрактных геометрических конструкций и численных мер. Кризис эмпирической методологии пропорций поставил новые задачи, связанные с более глубокой интеграцией в сфере интересов теории архитектурных пропорций математических, философских и физических моделей пространства (19,20). В этом отношении, физико-математические теории ХХ века, а так же философские работы, связанные с рефлексией результатов современной физики, представляют особую сферу для исследования категории гармонии вообще, гармонии в архитектурной геометрии, в частности.

1.3. Физика и геометрия природы. Как показывает анализ, современная физика пока не имеет готовых идей о законах и геометрии пространства-времени, приложимых к архитектуре в части сопоставимости физической и архитектурной геометрий. Даже обнадеживающие в начале ХХ века разработки А. Эйнштейна, сначала, в специальной (СТО), а потом и в общей (ОТО) теориях относительности, не привели к ожидаемым результатам. Практически, для всех областей знаний (за пределами физики), пространство-время носит мифологическую форму отчужденного от реальности “сюрреалистического” бытия природы. Релятивизм, разрушивший классическую традицию, по существу так и не представил взамен более убедительной, доступной и априори очевидной для человека идеи геометрии пространства-времени.

В СТО четырехмерное пространство-время Минковского, подобно трехмерному пространству и времени классической физики, носит абсолютный характер. В известном смысле пространство Минковского является экстраполяцией абсолютного трехмерного пространства Исаака Ньютона на еще одно измерение (21). Пространство Минковского однородно и изотропно (но уже в четырех измерениях), т.е. аналогично пространству Ньютона: как в механике Ньютона, так и в СТО, пространство-время пассивно. Это тот же сосуд, внутри которого тела, поля и т.п., движутся, не оказывая обратного воздействия на пространство-время (21). А.Эйнштейн сам отказался от СТО, в которой новый принцип относительности еще следует материалистическим принципам классической механики Ньютона. Он следующим образом объяснял отказ от СТО: “Итак, прежний способ, заключающийся в определенном построении координат в пространственно-временном континууме, оказывается неприменимым; представляется, что не существует пути, который бы позволил приспособить к четырехмерному миру такие координатные системы, чтобы с помощью их можно было бы ожидать особенно простой формулировки законов природы. Поэтому не остается ничего другого, как признать все мыслимые координатные системы принципиально равноправными для описания природы” (21).

В ОТО Эйнштейн заложил основы геометризации уравнений материи. Дж. Уиллер так выразил идею Эйнштейна: “Я глубоко потрясен сознанием всего величия пророческой мечты Эйнштейна, владевшей им на протяжении последних 40 лет его жизни. Я спрашиваю себя, как воплощается сегодня надежда Эйнштейна понять материю как форму проявления пустого искривленного пространства-времени. Его давняя мечта, так и не осуществленная им на протяжении всей его жизни и к осуществлению которой не приблизились еще и сегодня, может быть выражена древним изречением “все есть ничто”. Сегодня эту мысль можно высказать в виде рабочей гипотезы: материя есть возбужденное состояние динамической геометрии” (16).

Как отмечает Г.И.Шипов (22) так же как в СТО, так и в ОТО Эйнштейну не удалось преодолеть фундаментальное и принципиальное противоречие, свойственное абсолютной системе отсчета Ньютона: пространство-время и материя по прежнему представляют собою раздельные сущности. Будущее теории пространства-времени, которая бы устранила это противоречие, связывается с физическим вакуумом, как некоторой первоматерии, положившей начало вещественной эволюции Вселенной (11,21,22). Геометрия этой не квантованной субстанции связана с кручениями и лишена привычных представлений о трансляционных координатах пространства-времени (22). В частности, концепция физического вакуума Г.И.Шипова (22), базируется на ОТО А.Эйнштейна, но представляет движение в 10-мерной форме, где к 4 трансляционным координатам пространства-времени приложены 6 торсионных уравнений, описывающих изменение ориентации четырехмерного пространства-времени (три уравнения Эйлера, описывающих вращательное движение твердого тела для центра масс, и 3 неголономных координаты – приращения углов Эйлера, описывающих реальное, а не координатное, как у А.Эйнштейна, вращение).

Современное направление познания физического движения связывается с абсолютно геометризированными уравнениями движения, исключающими его классические характеристики (массу, энергию, импульс и т.д.). Но как бы ни подтверждался опытными данными предельно геометризированный подход к описанию природы, проблема понимания и объяснения объективных законов движения материи (равно как и причинно-следственное обоснование идей геометризации) остается открытой. Неразрешенность фундаментальной для физики проблематики, связанной с силами инерции (реальны ли они вообще? что является их источником? являются ли они внешними или внутренними по отношению к изолированной системе?) (22), является иллюстрацией скромной реализации в естествознании конца ХХ века, идей начала ХХ века.

1.4. Математика и физические модели материи. Кризис в естествознании косвенно отражает и прикладные проблемы математики. Применяемые в физике математические средства, не всегда доступны, не только специалистам другим областей, но даже ограниченному кругу физиков. В тоже время априори очевидно, что живые системы, органические формы природы пользуются какими-то чрезвычайно простыми механизмами вычислений, тесно связанными с особенностями симметрии их организации.

Одна из прикладных к физике проблем математики связана с интегральным исчислением, при котором, например, для зарядов и фотонов (как точечных масс), интегрирование ведется в пределах от 0 до, в результате чего соответствующие интегралы обращаются в бесконечность. Создатель квантовой электродинамики П.Дирак (22) эту проблему сформулировал в радикальной форме: “Правильный вывод состоит в том, что основные уравнения неверны. Их нужно существенно изменить, с тем, чтобы в теории вообще не возникали бесконечности и чтобы уравнения решались точно, по обычным правилам, без всяких трудностей. Это условие потребует каких-то очень серьезных изменений: небольшие изменения ничего не дадут”.

Существуют проблемы, связанные с математикой мнимых и комплексных чисел. Появившись в математике как пробочный продукт операций с действительными числами, мнимые и комплексные числа долгое время не могли получить геометрической интерпретации, не говоря о физической (И.К.Андронов, Математика действительных и комплексных чисел, - М.: Просвещение, 1975 г, с.96-115). Появление мнимых чисел в физике вызывало серьезные теоретические споры, а их физическое толкование, например, в волновой функции Шредингера Максом Борном, связывалось с вероятностными характеристиками движения в микромире (11).

Подобные споры, после представления Минковским геометрической интерпретации пространства-времени, были связаны с правомочностью включения мнимой единицы () в уравнения. Это произошло после того, как в 1905 году Пуанкаре обнаружил, что преобразования Лоренца математически соответствуют повороту в четырехмерном пространстве имеющем три пространственных измерения и одно временное измерение - три действительных координаты х, у, z и мнимую координату времени ict. В 1908 году Минковский завершил построение четырехмерной модели пространства-времени. В соответствии с подходом Минковского, вместо действительной сt можно использовать мнимую ict. Четырехмерные координаты, в которых используется мнимое время, называют координатами Минковского, в физике используются ограниченно, носят название Галилеевых координат и, по мнению физиков, более пригодны для глубокого анализа явлений, однако требуют усложнения математического аппарата (21).

Утверждение Минковского о единой природе пространства и времени вызвало критику ученых. В частности Дж. Уиллер отмечает: “Но теперь уже понимают, что нельзя преувеличивать утверждений Минковского. Совершенно справедливо, что время и пространство, неразделимые части единого целого. Однако неверно, что время качественно то же самое, что пространство. Почему же это неверно? ….. Какой же еще может быть к ним законный подход, как не равноправный, в формуле для пространственно-подобного интервала? Равноправный подход – конечно, но одинаковая природа - никак нет! В этой формуле есть знак минус, и его не изгнать оттуда никакими уловками. Знак минус отражает разную природу пространства и времени. Перейти к мнимому числу– вовсе не означает избавиться от этого “минуса”. Это случилось бы, если бы величина it была реальной, но она мнима. Нет часов, которые бы показывали секунд или метров. Реальные часы показывают реальное время, например t = 7сек. Поэтому член (время) всегда противоположен по знаку (расстоянию). Никакими закручиваниями и поворотами никогда не удастся заставить оба знака совпасть друг с другом” (14).

Аналогичную точку зрения по поводу мнимой единицы высказывает Э.Шмутцер: “…с помощью искусственного приема – введения мнимой единицы i - мы чисто формально наделяем время теми же качествами, что и пространство. Это дает возможность обобщить понятие вращения в трехмерном пространстве на четырехмерное пространство. Впрочем, это чисто математический трюк, за которым не кроется никакого физического смысла, но который оказывается полезным для некоторых целей” (21). Уравнения физики (волновая функция Шредингера (11), античастицы П.Дирака (11), теория физического вакуума Г.И.Шипова (22) и другие) вынужденно включают мнимую единицу, связывая с ней вероятностные характеристики движения. Представляется, что вероятностная трактовка не снимает проблем физической интерпретации мнимых и комплексных чисел в физике.

1.5. Философия, математика, диалектика. Математика, долгое время развивавшаяся в направлении узкой специализации, в самой себе, сегодня нуждается в синтезе и диалектической классификации математического знания, обслуживающего естественнонаучные исследования. Здесь уместно вспомнить о попытках Ф.Энгельса в “Диалектике природы” провести классификацию форм движения материи и соответственно классификацию наук, изучающих эти формы, опираясь на исследование диалектического содержания математики, механики, физики, химии, биологии (23). При этом Энгельс в математике выделял проблему кажущейся априорности математических абстракций: “Так называемые аксиомы математики – это те немногое мыслительные определения, которые необходимы в математике для исходного пути… Спенсер прав в том отношении, что кажущаяся нам самоочевидность этих аксиом унаследована нами. Они доказуемы диалектически, поскольку они не чистые тавтологии” (23). Иначе, Ф.Энгельс указывает на то, что в простых числовых величинах (1;-1;; 0), и в простых операциях (сложение, вычитание, умножение и деление), скрыты априори очевидные законы диалектики: закон единства и борьбы противоположностей, закон перехода количественных изменений в качественные, закон диалектического отрицания. Очевидность этих законов в действительности является естественной способностью человеческого сознания, а, следовательно, и естественной способностью диалектического отражения природы человеком.

Развитие естествознания сегодня требует философско-математического переосмысления таких системообразующих категорий как “относительное” и “абсолютное”. Требуется внедрение новых идей в понимание систем отсчета пространства-времени, неотделимых от движения самой материи. Накопленные в различных областях знания, а так же множество конструктивных идей в “пограничных зонах” смежных областей знаний, еще не получивших статуса научного, позволяют надеяться на возможность разработки геометрических моделей, способных объективно отражать законы движения в простой, классической форме, естественной для чувственного человеческого восприятия.

2. ПРИНЦИП СИММЕТРИИ

“Насколько я могу судить, все априорные утверждения физики имеют своим источником симметрию”

Weyl H. Symmetry–Princeton: Princeton Universal Press,1952

2.1. Методология естествознания. В качестве методологической основы анализа геометрических идей в современном естествознании (в плане их применения в теориях пропорций) могут быть принципы, на которые Э.Шмутцер (21) указывает как на основные, для создания физической теории: принцип простоты (максимально полное описание с помощью минимального числа законов); принцип ковариантности (независимость законов, наполненных физическим содержанием от субъекта и произвольно выбираемых параметров системы отсчета); геометрические основы (возможен переход к геометрии с кручениями); квантовый характер (выход за рамки классических представлений); правила перестановок и динамические законы; симметрия; причинность; принцип непрерывности познания (законы на более высоком уровне включают нижние, как частные случаи). Исследование геометрических моделей в физике с позиции соблюдения принципа симметрии, и его преемственности при переходе с одних уровней на другие, может быть принято для анализа проблем геометрии архитектурных пропорций.

2.2. Принцип непрерывности познания. Принцип непрерывности познания предполагает естественный переход от старой теорий к новой, корректный ввод новых представлений и процедур преобразований, связанных с математическим переоформлением прошлого знания. Анализируя проблемы геометрии релятивистской физики ХХ века и следуя принципу непрерывности в познании, мы должны: 1) вернуться к той исторической ситуации, когда была создана теория относительности; 2) к причинам отрицания СТО и разработки ОТО; 3) к тому фундаментальному открытию, которое привело к отрицанию абсолютной системы отсчета Ньютона - к открытию конечной величины скорости света.

2.3. Принцип симметрии. Принцип симметрии один из ведущих принципов познания. Он лежит в фундаменте диалектики. Законы единства и борьбы противоположностей по существу отражают основной закон симметрии связанный с различием и тождеством диалектических сторон явления, составляющих сущность его движения, развития.

Пьер Кюри рассматривал симметрию как результат диалектического взаимодействия объекта со средой. Он придавал симметрии огромную роль в исследовании физических явлений: “Думаю, что представляет интерес ввести в изучение физических явлений понятие о симметрии, столь привычной кристаллографам” (Пьер Кюри, 1894г. “О симметрии физических явлений; симметрии электрического и магнитного поля”). По Кюри, симметрия порождающей среды накладывается на симметрию тела, образующегося в этой среде. Получившаяся в результате форма тела сохраняет только те элементы собственной симметрии, которые совпадают с наложенными на него элементами среды, т.е. сохраняются только тождественные свойства (среда, тело–диалектические противоположности, порожденный объект - их единство).

Понятие симметрии, развиваемое Пьером Кюри, шире обыденного понимания симметрии как, например, зеркальное равновесие масс, и предполагает, прежде всего, симметрию как движение, как развитие, как отношение отрицания единичных свойств тела и среды и утверждения их общих свойств в форме особенного, порожденного ими нового тела (2,10,18). Другим примером динамической симметрии является процесс метаболизма, свойственный органическим формам, как единство синтеза и распада. При очевидном различии (жизнь и смерть), эти процессы находятся в отношении симметрии.

В научной методологии, смысл симметрии (отношений) так же предполагает, что фундаментальный закон должен быть инвариантным по отношению к действию некоторой операции симметрии (преобразования координат, функциональные преобразования и т.п.).

3. СИММЕТРИЯ В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

3.1. Геометрия специальной теории относительности. Соответствует ли принципам симметрии модель пространства-времени, разработанная специальной теорией относительности с целью органичного включения открытой физической постоянной – скорости света в физическую теорию, взамен представлениям Ньютона, об отсутствии ограничений на скорость?

Геометрическим способом введения в физику световой константы и светоподобного интервала является псевдоевклидова геометрия (теорема Пифагора, связывающая в псевдоевклидовой метрике абсолютный и относительные интервалы пространства и времени). Пространство-время представлено ортогональными координатами и разделено образующими, для которых x = t (это взаимно-перпендикулярные, развернутые вокруг центра системы отсчета (x,t) под углом образующие (ct,-ct). Они разделяют ИСО на две области: область до световых скоростей и область сверхсветовых скоростей. Область до световых скоростей, в свою очередь, состоит из области прошлого и области будущего (Рис.1). Квадрат абсолютного интервала равен разности квадратов относительных интервалов пространства и времени:,.

3.2. Нарушение принципа симметрии специальной теорией относительности. Отметим следующие нарушения принципа симметрии в модели ИСО СТО:

1. Кроме скорости v (абсолютной скорости пробной частицы), и скорости с (абсолютной скорости света), в уравнениях присутствует скорость, физический смысл которой не ясен, кроме того, что она входит в выражение коэффициента Лоренцева сокращения (расширения). Как производная абсолютных скоростей v и c, она должна иметь аналогичный смысл и указывает на существование некоторого реального физического объекта, с движением которого она связана.

2. При равноправной v и c, отношения c/c = 1/1 = 1 и c/v = 1/ так же должны иметь смысл адекватный смыслу. Иначе, предположительно, в световой модели Вселенной должны существовать три типа равноправных ИСО, со своими коэффициентами сокращения (расширения).

3. Введение понятия светоподобного интервала, в связи с открытием в природе предельной скорости света (граничные параметры скоростей v=0, v=c), предполагает два типа равноправных ИСО, для которых состояние покоя формулируется относительно граничных параметров скорости света:, состояние покоя которой соответствует скорости v=0 (система отсчета Лоренца-Минковского в СТО) и, состояние покоя которой соответствует скорости света (фотон, как покоящаяся система). СТО не рассматривает такую равноправную. При заданном условии покоя v=c), покоится на образующих светоподобного конуса (сt ,-ct) на таких же законных основаниях как покоится при v=0. зеркальна. Если расширяется, то– сокращается. Скорость частицы в -, = c/v=. Так как - v в и в связаны скоростью света (или светоподобным интервалом), и являются относительными, связанными между собой светоподобным интервалом, подсистемами одной и той же системы отсчета. Иначе, светоподобный интервал это не только предельная величина скорости, что утверждает СТО, но, прежде всего, скорость, связывающая две равноправные, но качественно различные ИСО покоя в движении одной и той же “пробной массы”, т.е. системы отсчета присущих ей различных форм движения, например, как частицы - v и как излучения -. Эти скорости могут быть связаны с различной плотностью массы пробной частицы (например, v – скорость положительной плотности +p и - скорость отрицательной плотности -p).

4. В связи с тем, что в ИСО Минковского часть пространства-времени связана с досветовыми скоростями (конуса будущего и прошлого), а часть - со сверхсветовыми скоростями, она не только полностью не определена, но допускает нарушение исходного принципа своей конструкции – движение со сверхсветовой скоростью. Если допустить существование сверхсветовых скоростей, мы, при конструировании ИСО, должны отказаться от скорости света, связанного с ней и определяться в новом геометрическом принципе ИСО. Но это уже будет совершенно другая система отсчета.

5. В уравнении закона сохранения (например, для абсолютного интервала массы покоя):

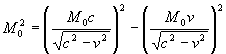1)

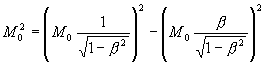
2)

Где - абсолютный интервал t-подобной массы покоя

- относительный интервал t-подобной энергии;

- относительный интервал x-подобного импульса

об абсолютной природе интервала можно говорить лишь в относительном смысле, в связи с применением, так как по аналогии с правой частью равенств 1) и 2), абсолютный интервал в левой части равенства, может быть выражен в форме. Интервал абсолютен только при.

Поскольку 1/1, 1/ не могут рассматриваться иначе, как равноправные (наравне с), ясно, что масса покоя 1),2) теряет свой абсолютный смысл, если ее рассматривать относительно = 1/ или = 1/1, т.е. представление абсолютности интервала 2) справедливо лишь при.

3.3. Незавершенность геометрии ИСО в СТО. Внутренние (нарушение симметрии в уравнении скоростей, наличие несистемных областей пространства-времени) и внешние (независимость системы отсчета от материи, неточность отражения движения в связи с гравитационными эффектами) противоречия ИСО в СТО, необоснованность выражения пространственно-временного континуума теоремой Пифагора в связи с принципиально различной природой пространства (как протяженной характеристики) и времени (как длительной характеристики), позволяют сделать вывод, что ограниченность ИСО в СТО связана, прежде всего, с незавершенностью, неразвернутостью геометрии ее координатного пространства.

4. ПРЕОБРАЗОВАНИЕ СИСТЕМЫ ОТСЧЕТА МИНКОВСКОГО

С учетом вышесказанного, преобразование ИСО СТО Минковского, с целью снятия противоречий, предполагает две главных процедуры (рис.1, рис.2):

4.1. Мнимый поворот координатных осей пространства-времени Минковского.

А) Мнимый поворот х-подобной оси х (ИСО СТО) на до совмещения с отрицательной полуосью времени -t (конус прошлого) и превращением ее в отрицательную мнимую величину -iх, противонаправленную времени t (Г.Корн, Т.Корн. Справочник по математике, -М.: Наука, 1973, с.31-33). Закон сохранения (для интервала массы покоя) приобретает следующее выражение:

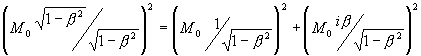3)

Поворот не изменил отношений в формуле 2). Пространственный вектор приобрел отрицательный знак относительно положительного вектора и заменил суммой разность между двумя квадратами относительных интервалов ИСО СТО, но при этом, вошедшая в выражение импульса мнимая единица, вернула нас вновь к разности квадратов интервалов.

Б) Этому повороту соответствует аналогичный поворот и совмещение -ct и ct (далее) и, кроме того, общий поворот совмещенных осей () на в положение, перпендикулярное совмещенным осям (T,iХ), т.е в положение, занимаемое осью пространства ИСО СТО :

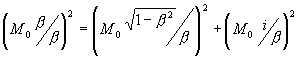4)

Относительный интервал энергии () получил зеркальную, x-подобную форму, относительный интервал импульса (Мо* 1/), наоборот, t-подобную форму, абсолютный интервал Мо* / – x-подобную форму. Взятые относительно светоподобного интервала = 1/1, уравнения приобретают абсолютно идентичную количественную форму с зеркальной метрикой: свойство абсолютного интервала приобретает энергия (x-подобная и t-подобная), абсолютные интервалы в уравнениях 3) и 4) приобретают роль относительных импульсов. Абсолютные, комплексные: t-подобный и x-подобный интервалы энергии связывают в псевдоевклидовой геометрии Минковского пары относительных осевых противоположно направленных импульсов, при этом :

5)

6)

Природа псевдоевклидовой метрики связана с осевым (положительным и отрицательным) направлением относительных импульсов. Абсолютный интервал - комплексная величина. Квадрат абсолютного интервала энергии - полная энергия оси, равная разности квадратов импульсов (при скоростях и i). С учетом мнимой величины, не исключена возможность того, что разность квадратов импульсов в правой части равенства - это разность кинетической и потенциальной энергий. Характерной особенностью уравнений, кроме их зеркальной симметрии, является то, что при действительном и мнимом импульсах, интервал энергии выступает как абсолютный, комплексный, скалярный интервал, но в случае, если мнимый импульс приобретает действительную форму, комплексная энергия приобретает действительную форму и при = =, (прис), ее интервал равен нулю. В ИСО СТО условие равенства относительных интервалов выполняется при =1 (при скорости света). Второй особенностью является то, что из уравнений сохранения (в связи с переходом к = 1/1) , устранены бесконечные величины (уравнения 5), 6)). Кроме того, x-подобные (так же как и t-подобные) полуоси связаны теоремой Пифагора в Евклидовой метрике. При всех значениях разрешенных скоростей осевые и взаимно ортогональны.

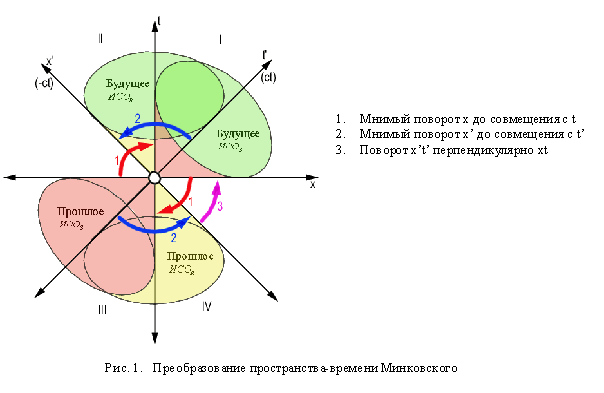
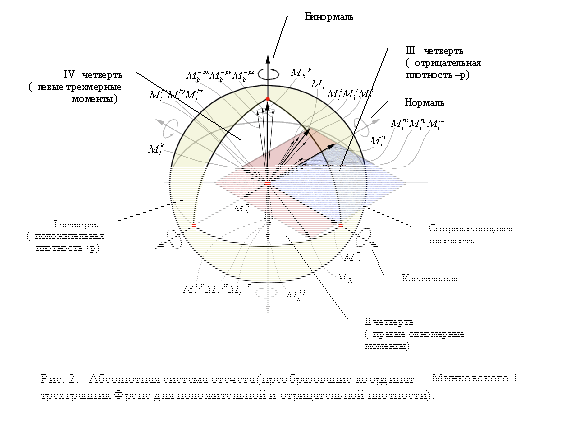
4.2. Подвижный трехгранник Френе и пространство кручений. Поскольку вновь образованная, за счет зеркальной симметрии, ИСО уже не может быть связана с поступательным движением (обе ИСО имеют единый центр, и следовательно движение может быть связано с изменением направления скорости, в условиях отсутствия трансляций), поскольку при изменении скоростей координатное пространство не подвержено преобразованиям с кручениями осей подобно ИСО СТО, она может рассматриваться только как вращательная (торсионная) система отсчета, а движение в ней (расширение или сокращение), может рассматриваться как функция изменения состояния пробной массы (объема, плотности). В связи с вышесказанным, ИСО может интерпретироваться как комплексная форма соединения мнимого и действительного “подвижных” трехгранников Френе для случая кручений по направлениям базисных (нормального, касательного, бинормального) векторов. При этом, плоскость векторов нормального и касательного моментов, соответствующая относительным импульсам в и, представляется как соприкасающаяся плоскость, а третий вектор, ортогональный двум указанным – бинормаль, равен векторному произведению нормального и касательного векторов (Г.Корн, Т.Корн. Справочник по математике. – М.: Наука, 1973г., с.521-524).

Характерно, что нормаль (или главная нормаль), касательная и бинормаль – компоненты базисных векторов трехгранника Френе, связаны с кривизной и кручением пространства и лежат в основе тензорного определения кривизны пространства (например, тензоры Риччи второго ранга), примененного А.Эйнштейном в ОТО. В связи с комплексной формой выражения законов сохранения, ИСО представлена тремя (действительным, мнимым и комплексным) трехгранниками Френе. Результатом зеркальной симметрии двух трехгранников, подвижных в противоположных направлениях, является статичная система отсчета, в которой отсутствуют трансляционные координаты (т.е. отсутствует пространство-время). Потеря пространственно-временной определенности – цена перехода к шестимерному пространству кручений. В условиях зеркальной симметрии нормального и касательного базисных векторов, векторное произведение нормальной скорости (мнимой или действительной) на касательную (мнимую или действительную) в инерциальной системе отсчета будет иметь форму квадратов относительных скоростей соответственно = 11, ,.

Таким образом ИСО связана с кручениями, где: 1, и - относительные угловые скорости ; = 11, , - бинормальные (квадратичные) скорости. Импульсы и энергии в законах сохранения, соответственно, являются моментами (инерции) энергий и импульсов. Поскольку в полученной системе отсчета состояние покоя связано с = = или 0,707… скорости света, (при, связанной с массами положительной плотности и при, связанной с массами отрицательной плотности), состояние покоя результирующей системы будет характеризоваться нулевой плотностью покоя. (+p) + (-p) = 0, а сама система отсчета может рассматриваться как абсолютная система отсчета движения изолированной физической системы. Различие в метрике отдельных элементов системы отсчета отражает не отношения пространства и времени, а отношения между 3-мерными и 1-мерными элементами пространства скоростей (в частности нормальные и касательные скорости).

4.3. Уравнения законов сохранения в абсолютной системе отсчета. Геометрия преобразованной системы включает следующие основные законы сохранения (при следующих физических величинах):

- момент инерции (эквивалентный массе покоя),

1 - абсолютный интервал относительной угловой скорости 1 = с/с

- относительный интервал относительной угловой скорости = v/c, может, например, рассматриваться как угловая скорость положительной массы, как векторное разложение квадратичной бинормальной скорости на равные между собой нормальную и касательную скорости инерции положительной массы

- относительный интервал относительной угловой скорости может, рассматриваться как угловая скорость отрицательной массы, как векторное разложение квадратичной бинормальной скорости на равные между собою нормальную и касательную скорости инерции отрицательной массы

- угол между скоростью и скоростью 1

;;; -общая форма уравнения скоростей

Ниже, в принципиальной форме, приведены основные уравнения абсолютных и относительных интервалов моментов (в примерном виде по модулю), без учета изменения направлений векторов скоростей и мнимых характеристик крутящих моментов. Уравнения легко переводятся в чисто геометрическую форму для единичной сферы (при =1).

А) Относительные (нормальные и касательные правовинтовые и левовинтовые) моменты в соприкасающейся плоскости подвижного трехгранника Френе (всего - 4):

1а) - нормальный x-подобный интервал левого момента инерции

2а) - касательный x-подобный интервал левого момента инерции

3а) - нормальный t-подобный интервал правого момента инерции

4а) - касательный t-подобный интервал правого момента инерции

Б) Абсолютные (нормальные и касательные правовинтовые и левовинтовые) интервалы моментов инерции в соприкасающейся плоскости подвижного трехгранника Френе (всего – 4):

1б) - абсолютный x-подобный интервал (4-я четверть)

2b) - абсолютный t-подобный интервал правых (2-я четверть)

3b) - абсолютный осевой xt-подобный интервал нормальных (,) -моментов

4b) - абсолютный осевой xt-подобный интервал касательных (,) -моментов

В) Бинормальные 3х мерные моменты инерции (,) для (+P) и (-P) плотности на бинормали подвижного трехгранника Френе:

1в) - относительный интервал бинормального момента инерции -P плотности

2в) -относительный интервал бинормального момента инерции +P плотности

3в) абсолютный бинормальный момент инерции +P плотности

нормальный и касательный моменты инерции в соприкасающейся плоскости могут рассматриваться как производные (корни) от положительных и отрицательных бинормальных моментов: и, соответственно, могут принимать значения:;;;

4в) - относительный векторный бинормальный RL-момент инерции

где = - угол между и продолжением

5в) - относительный скалярный бинормальный RL-момент инерции

где = - угол между и продолжением

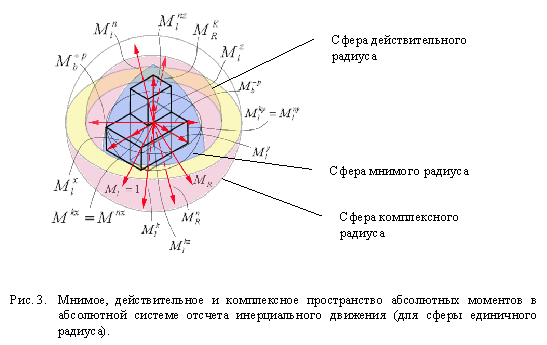
Кроме того, поскольку бинормальный момент является произведением нормального и касательного векторов, один из которых 3-мерный, бинормальный вектор представляется в его трехмерной проекции.

Г) Нормальное (действительное), касательное (мнимое) и бинормальное (комплексное) пространства 3-мерных x-подобных моментов.

1г) (, ,) – касательный x-подобный момент и его ХУZ-проекции

2г) () - нормальный x-подобный момент и его ХУZ -проекции

3г) ()- комплексный (результирующий) x-подобный момент и его ХУZ- проекции.

4г); 5г); 6г);

7г); 8г)

9г), при

10г), при

11г)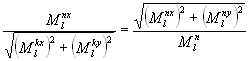; 12г)

Уравнениям x-подобных моментов инерциального движения в системе декартовых координат, соответствуют инвариантные уравнения в полярных координатах (угол восхождения радиуса равен углу склонения, угол восхождения радиуса равен минус удвоенный угол склонения), отражающие специфику симметрии геометрии комплексного пространства (рис.4). При всех значениях скоростей, для пространственных модулей характерны среднепропорциональные отношения (11г, 12г).

Приведенные уравнения (а всего с учетом x-подобных, t-подобных, xt-подобных моментов, интервалов и результирующих моментов в их более 50: -13 осевых на нормали, - 13 осевых на касательной, - 13 RL-винтовых, между x-подобной и t-подобной четвертями, - 16 осевых xt-подобных на бинормали) демонстрирует богатство отношений закона сохранения движения, определяя геометрию инерциального движения на всем () диапазоне скоростей. С учетом различных, возможных вариаций мнимых и действительных моментов, общее количество уравнений сохранения значительно больше. Подобное многообразие мнимых, действительных и комплексных отношений инерциального движения проявляется, вероятно, не только на “виртуальном” уровне микро-материи (в мире микрочастиц), но и на других, более сложных макро- и мега- уровнях организации материи.

Переход из ИСО СТО в абсолютную систему отсчета можно проиллюстрировать следующим образом. Внешний наблюдатель явлений, происходящих в ИСО, неудовлетворенный тем, что гравитационные эффекты не обеспечивают, неискаженных кривизной пространства-времени результатов наблюдений пробной массы, обнаруживает, что в наблюдаемой ИСО, кроме базового координатного пространства (), существует инвариантная, но зеркальная система координат (относительно). Переход в нее связан с зеркальными преобразованиями, заменой с (расширяющаяся) на (сокращающаяся). Заняв место в новой, он обнаруживает; что центры обоих ИСО, совпадают; что изменение скорости не связано, ни с перемещениями относительно центра, ни с преобразованиями координатного пространства; что он всегда находится, в общем, для обоих ИСО центре, но в зеркальной системе, привычное для него расширение массы, превратилось в сокращение. Зная, что относительные связаны между собой абсолютной скоростью света, он обнаруживает еще одну, третью, , (. = 1/1 = с/с), которая ни расширяется, ни сокращается, а всегда находится в состоянии покоя. Относительно третьей ИСО, движение исследуемой массы - суть взаимосвязанные процессы сжатия и расширения (относительно состояния покоя =) под действием правых и левых моментов кручения, положительных и отрицательных энергий плотности

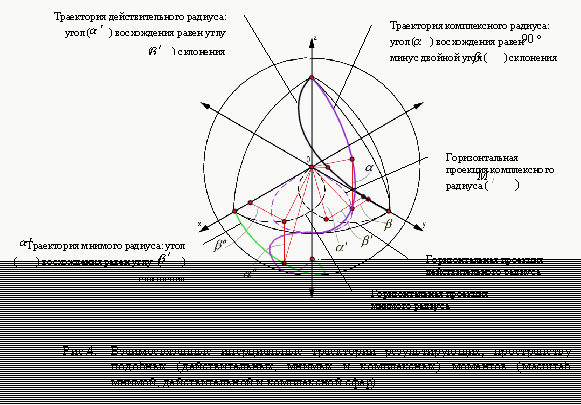
5. ОСНОВНЫЕ СВОЙСТВА АБСОЛЮТНОЙ СИСТЕМЫ ОТСЧЕТА.

5.1. Абсолютная система отсчета () является следствием соединения принятой в СТО (покой при v=0) и не выявленной в СТО (покой при v=c). Каждая ИСО представлена одной осью (нормалью или касательной) в соприкасающейся плоскости трехгранника Френе. Обе ИСО взаимно ортогональны. Результирующая представлена на бинормали и является следствием векторного произведения на. С другой стороны, мнимые и действительные, положительные и отрицательные моменты в соприкасающейся плоскости трехгранника Френе являются следствием квадратичного разложения бинормальных моментов. С мнимыми моментами могут быть связаны различные "виртуальные" эффекты (например, когда действительный бинормальный момент распадается на два мнимых момента). Координатные оси имеют переменную сигнатуру в зависимости от знака направления оси. В связи с вышесказанным, результирующая система отсчета может рассматриваться или как бинормаль, или как эквивалентная ей соприкасающаяся плоскость, что, безусловно, определяет ее специфику (т.е. дуализм) и может быть связано с различными, существенными в физике, эффектами.

5.2. имеет ортогональную 6-мерную систему пространства кручений. Мнимый и действительный трехгранники Френе, по положительным и отрицательным направлениям касательной и нормали, связаны абсолютными осевыми интервалами (принятым в СТО уравнением 4-мерного пространственно-временного континуума, но не для трансляций, а для 3-мерных, x-подобных и 1-мерных, t-подобных, противоположных по направлению, моментов инерции. О пространстве-времени мы говорим условно, имея в виду различие в метрике (как между 3-мерной касательной скоростью и 1-мерной нормальной скоростью).

5.3. Геометрия включает три взаимосвязанных на афинной плоскости геометрии: геометрия Минковского (М-геометрия), геометрия Евклида (Е-геометрия), геометрия Галилея (Г-геометрия). Для этих геометрий действительны: аксиома о параллельных прямых, определение координатного пространства (ортогональная система), определение расстояний (теорема Пифагора). Можно говорить о том, чтосинтезирует три А-геометрии в целостную геометрическую систему - МЕГа – геометрию (4). В частности, положительные и отрицательные осевые моменты в соприкасающейся плоскости связаны абсолютными светоподобными моментами в М-геометрии; относительные, нормальные и касательные “левые” моменты связаны абсолютным x-подобным моментом в Е-геометрии; нормальные и касательные “правые” моменты связаны абсолютным t-подобным моментом в Е-геометрии; положительные и отрицательные бинормальные моменты связаны абсолютным бинормальным моментом в Г-геометрии. Е-геометрия и М-геометрия являются следствием векторного разложением Г-геометрии.

5.4. Система координат остается ортогональной для всех состояний инерциального движения (в отличии от координат пространства-времени ИСО ОТО, где действительные кручения массы пробной частицы перенесены на мнимые преобразования (повороты) координатных осей при изменении скорости. В связи с отсутствием гравитационных эффектов (пробная частица адекватна всей области координатного пространства) и отсутствием ограничений на величину пробной массы частицы (сняты ограничения гравитации), предполагает принципиально новое и отличное от ИСО СТО определение инерциального движения (например, в отличии от 14). В частности, в геометрии кручений теряет смысл трансляционная метрика, а движение (изменение скорости) связывается с изменением состояния (плотности, размера) пробной частицы, без ограничений на ее массу.

5.5. Инерциальное самодвижение в является следствием противодействия положительной и отрицательной плотности (экстремум при = 1 и = 0 в I и III четвертях единичной окружности, рис.2), с одной стороны, и противодействия результирующих x-подобного (левого) и t-подобного (правого) моментов инерции (экстремум при = во II и IV четвертях рис.2). Поскольку состояние покоя плотности связано с максимальной энергией кручений (энергия - как скалярное произведение x-подобных на t-подобные моменты) и, наоборот, состояние покоя кручений связано с максимальной энергией плотности (энергия - как векторное произведение x-подобных и t-подобных моментов), самодвижение в - результат противодействия энергии плотности и энергии кручений.

5.6. Включение в ИСО мнимых величин позволяет приблизиться к новому пониманию природы сил инерции и по новому ставит диалектику отношений внутреннего и внешнего. В частности, действительный, но отрицательный бинормальный момент, распадающийся на два мнимых момента в соприкасающейся плоскости, по форме является “внешней силой”, по отношению к действительным моментам в соприкасающейся плоскости, как “внутренним силам”. В связи с этим, законы сохранения интервалов в замкнутой, связывающие мнимые и действительные моменты, могут рассматриваться как уравнения внешних и внутренних сил инерции изолированной системы. Самодвижение есть следствие взаимодействия собственных “внешних” и “внутренних” сил изолированной пробной массы. Отношения равновесия (сохранения количества движения) самодвижения, могут рассматриваться в форме столкновения энергий (масс) положительной и отрицательной плотности.

5.7. Инерциальное самодвижение может быть связано, как с представлениями Ньютона (21), который утверждал, что центробежная сила, в отличии от прочих сил, берет свое начало в абсолютно пустом пространстве, так и с представлениями Э.Маха (“принцип Маха”), который считал, что космические массы (“далекие массы”) создают, после усреднения их относительных движений, выделенную систему отсчета (космическую систему Маха), и которая принимается нами за абсолютно существующее пространство (21). Позиции Ньютона и Маха близки развиваемой концепции в том смысле, что предполагают существование некоторых мнимых, "внешних" сил, необходимо связанных с действительным движением.

5.8. Инерциальное самодвижение может быть связано с некоторыми следствиями теории физического вакуума Г.И.Шипова. В частности, решения уравнений, описывающих вакуумное возбуждение без массы и заряда, но обладающие трехмерным спином. Как указывает Шипов: “Поля, имеющие нулевую энергию, но способные к взаимодействию (например вращать плоскость поляризации света) в физике встречаются впервые, поэтому при их изучении надо быть готовым к неожиданным физическим эффектам. Например, потенциальная энергия взаимодействия решения уравнения равна нулю, однако “вращательная траектория” материальной частицы, подчиняющаяся уравнениям движения, будет меняться, передавая “вращательную” информацию. Такие поля можно было бы определить как информационные поля, переносящие торсионную информацию о физическом объекте” (22 с.188)

5.9. 6-мерное пространство кручений, отсутствие трансляционной метрики указывает на то что, система отсчета описывает среды, отличные от твердых тел. Это могут быть упругие среды (в квантовой теории поля – физический вакуум). Если связана с физическим вакуумом, что очень вероятно при ее исключительно торсионной геометрии, то абсолютный физический вакуум следует определять как неквантованное состояние первоматерии, без ограничений на плотность, в отличие от традиционного понимания (предельно растянутая материя, пустота). В соответствии EGS-концепцией А.Акимова (22), можно предполагать связь трех принципиальных форм закона сохранения в с основными поляризационными состояниями вакуума - по осям нормали и касательной - гравитационная поляризация, с t-подобными (II четверть) и x-подобными моментами (IV четверть) – электрон-позитронная поляризация, с бинормальными моментами - торсионная поляризация. Связи этих состояний поляризации может так же рассматриваться в контексте отмеченной выше связи между геометриями Галилея, Евклида и Минковского.

5.10. Уравнения инерциального движения однозначно определены на всем диапазоне скоростей, поддаются полной геометризации (взаимное сокращение массы в правой и левой частях равенства). Пространство моментов энергий импульсов может рассматриваться в отношениях 6-мерного векторного пространства кручений сферы единичного радиуса для единичной массы (мнимая, действительная и комплексная геометрии с угловыми скоростями, представленными тригонометрическими функциями). Философское и математическое содержание развиваемой идеи симметрии связано с качественно новым математическим определением понятия точки. Традиционное определение точки, связанное с трансляционными преобразованиями пространства в точку (объем – плоскость – линия - точка), отражают лишь относительное изменение масштаба, но не вносят в определение точки нового качества, отличного от трехмерного пространства. Как бы мы ни старались описывать точку, как некоторую микроскопическую величину, ее трехмерная природа сохраняется, она не может быть выделена как новое качество никакими изменениями “калибра”. В новом смысле, точка определяется в безразмерном 6-мерном пространстве кручений, связанном действительной, мнимой и комплексной системой геометрий на Афинной плоскости (геометрии Евклида, Галилея, Минковского). Дальнейшая трансформация точки в трехмерное пространство теперь связана не с ее трехмерными трансляциями вовне, а с внутренним процессом ее деления (квантования). В мире кручений физика и геометрия адекватны и геометрия выступает как абсолютная система идеально геометризированных физических уравнений, соответствующих природе материи.

5.11. Очевидно, что, взятая относительно и , приводится обратным путем (с учетом явлений связанных с зеркальной симметрией и комплексным трехгранником Френе) в относительные ИСО СТО, с преобразованием абсолютных интервалов в относительные и наоборот, относительных в абсолютные. Геометрия относительных, локальных ИСО будет связана с применением коэффициентов расширения (сокращения). Но относительно, расширение или сокращение локальных ИСО будет иметь мнимую форму (подобно “мнимым” киноэффектам при монтаже сказочных фильмов с превращениями карликов в великанов, и, наоборот, благодаря изменению масштаба, калибра окружающего ландшафта). С учетом эффектов зеркальной симметрии, уравнения инвариантны уравнениям ИСО СТО, или другим физическим уравнениям, которые включают 4-мерный пространственно-временной континуум ИСО СТО. Вероятно, что 6-мерная торсионная геометрия, согласуется с торсионными координатами Г.И.Шипова (с 6-ю угловыми координатами - тремя пространственными углами и тремя псевдоевклидовыми углами - 10-мерного пространства событий произвольно ускоренных четырехмерных систем отсчета) концепции физического вакуума).

5.12. Преобразование ИСО СТО переводит ее с частного случая ОТО в абсолютную, всеобщую систему отсчета. изначально лежит в основе общего принципа относительности Эйнштейна, объявляющего равноправность локальных, ускоренных инерциальных систем отсчета, является его обоснованием (как и обоснованием геометризации уравнений материи ОТО). в качественно новой форме утверждает принципы классической механики. Являясь синтетической основой соединения математики и естественно-научного знания, (в основе симметрии которой лежат диалектические противоположности – “правое-левое”, “положительное-отрицательное” - и их тождество, разрешаемое в законах сохранения интервалов), является системообразующей моделью для философского познания природы в категориях и законах диалектики. Иначе, развитие развиваемой концепции симметрии, в перспективе, предполагает новый уровень понимания природы, в основе которого лежит гармоничный синтез математики, философии и естествознания.

6. ГИПОТЕЗЫ ФИЗИЧЕСКИХ ЯВЛЕНИЙ В АБСОЛЮТНОЙ ИНЕРЦИАЛЬНОЙ СИСТЕМЕ ОТСЧЕТА

“Ты – Един, начало всех чисел и основа всех построений.

Ты - Един и Твое Единство никогда не умаляется и никогда не расширяется и не может быть изменено”

(Из Гимна Абсолюту – Парабраману, Единому Божественному началу С.В.Стульгинскис. Космические легенды востока –М.: Сфера, 1997. с.22)

6.1. Новые идеи симметрии в современной физике. Способность спинорного поля описывать полуцелый спин элементарной частицы Вернер Гейзенберг (1901 – 1976) положил в основу первичного поля материи, связывая с ним нелинейное уравнение на основании предположения, что существование элементарной частицы обусловлено ее взаимодействием с самой собой. В уравнение поля была заложена глубокая симметрия, при достаточно сложном математическом обеспечении (21). Исходя из законов симметрии, Я.Терлецкий предположил, что у каждого физического поля с положительной плотностью энергии р+>0 существует “двойник”, поле с отрицательной плотностью энергии р-<0, и что, при рождении частиц из физического вакуума, должны рождаться частицы как с положительной, так и с отрицательной массой. Положительные массы притягиваются между собой, образуя плотное звездное вещество, отрицательные отталкиваются, равномерно распределяясь по Вселенной (22). Опираясь на гипотезу симметрии Я.Трелецкого, Г.Шипов (22) предполагает рождение частиц четверками, “квадригами”, (положительная и отрицательная массы с положительными и отрицательными зарядами). В теории Г.Шипова рождение “квадриг” соответствует расщеплению уравнений Картана геометрии абсолютного параллелизма (геометрия абсолютного параллелизма - А4 так же лежит в основе псевдоевклидовой геометрии Минковского в СТО) на торсионные уравнения правого и левого мира. По Г.Шипову, физический вакуум, в процессе возбуждения, распадается на левые и правые вакуумные поля кручения, каждое из которых включает как материю, так и антиматерию, при общей нейтральности замкнутой физической системы, как по плотности /(+p)+(-p)=0/, так и по заряду /(+e)+(-e) =0/.

Пространство кручений, его абсолютная геометрическая форма и генетическая связь с 4-мерным пространством-временем ИСО СТО, позволяет утверждать за ним универсальную способность описывать, в простой и точной форме, те состояния физической материи, к которым ОТО Эйнштейна и теория всеобщей относительности Г.Шипова, базирующаяся на 4-мерных трансляционных координатах с добавлением 6 торсионных координат, подходят со стороны теоретической интерпретации результатов физического опыта с привлечением сложных геометрий (в частности, уравнений и систем уравнений геометрии абсолютного параллелизма Килинга-Картана, Эйнштейна-Янга-Милса, Кармели, Ньюмена-Пенроуза, Шипова-Эйнштейна, Шипова в приложении к ОТО).

Свойства симметрии, а так же ряд приведенных выше идей физиков, связанных с общими принципами симметрии в движении материи, позволяют в самом общем виде высказать некоторые гипотезы и предположения о возможности применения в моделировании разнообразных физических явлений.

6.2. Колебания в форме математического маятника. Простые колебания массы в форме математического маятника осуществляются при последовательной актуализации мнимых моментов на положительных и отрицательных полуосях соприкасающейся плоскости. При одном действительном относительном моменте (например, или ) будет всегда один действительный относительный, но отрицательный бинормальный момент - (i* i= или i * i=), который будет связан с изменением знака плотности энергии и знака моментов кручений. Четыре последовательные фазы инерциального колебания математического маятника: а) падение "справа" под действием силы тяжести, б) подъем "влево" за счет касательной скорости, в) падение "слева" под действием силы тяжести, г) подъем "вправо" за счет касательной скорости и т.д., для колебания вакуума будут иметь следующий примерную форму моментов в соприкасающейся плоскости:

А) (; i; i; i) - расширение из сжатого состояния до состояния равновесия при =, при нормальной угловой скорости расширения;

Б) i; ; i; i) - расширение из сжатого состояния после равновесия при =, при касательной угловой скорости расширения;

В) ( i; i; ; i) - сжатие из растянутого состояния до равновесия при =, при нормальной угловой скорости сжатия;

Г) ( i; i ; i ; )- сжатие из растянутого состояния после равновесия при =, при касательной угловой скорости сжатия.

В каждый момент масса (сфера) будет представлена новой величиной объема и новой величиной плотности (единой по всему объему). Предельные характеристики плотности и, соответственно, предельные характеристики объема реализуются при =1 и =0. Среднее значение объема и плотности реализуются при =. Пространственные механические перемещения маятника здесь представляются колебаниями плотности, т.е. связаны с изменением субстанциональных свойств пробной массы.

В условиях значительных по размерам масс, колебания в форме математического маятника возможно будут затухающими, в связи с проявлением локальных (негармонических) колебаний плотности (сферические области различной плотности), которые будут противодействовать инерции, тормозить колебания, что, в конечном счете, должно привести массу к среднему состоянию покоя при =.

6.3. Гармонические синусоидальные колебания плотности массы. В связи с максимальным энергетическим потенциалом кручений, при = потенциальное состояние покоя положительной и отрицательной плотности не достижимо. Следствием разрешения этого противоречия будет самовозбуждение гармонических колебаний (сферических волн) сопровождающихся расслоением плотности (чередующиеся сферы положительной и отрицательной плотности) при сохранении нулевого результирующего момента. Колебания могут начаться самопроизвольно, нарастать и, при сохранении нулевого результирующего момента (при симметричном возрастании положительной и отрицательной плотности), осуществляться в условиях стационарного объема (Vcт).

В условиях Vcт, центр и оболочка сферы пробной “массы-вселенной”(как мнимые, “внешние” границы) будут подобны отражателям волн сжатия-растяжения (защемленная с двух концов стоячая волна) и стимулировать процесс колебания в режиме ускорения и самосинхронизации. Колебания в каждом слое будет протекать в четырех фазах (математический маятник). Колебания в условиях расслоения плотности вероятно будут связаны с изменением температур (сжатие +Т, растяжение -Т), проявлением электромагнетизма и термодинамических эффектов (типа четырехтактного цикла Карно (23), способствуя развитию процесса расслоения вакуума. Механические, электромагнитные и термодинамические эффекты будут проявляться в неотделимой, друг от друга, форме.

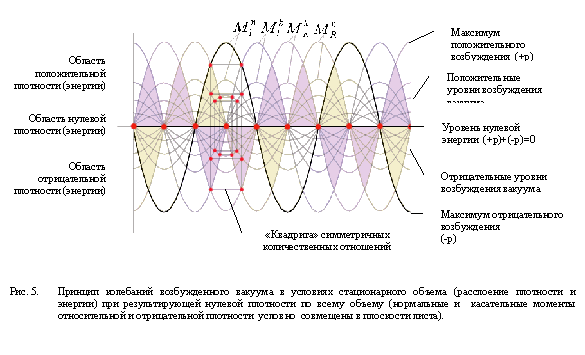
Графики колебаний относительных нормальных и касательных моментов в соприкасающейся плоскости имеют синусоидальную форму (примерно как на рис.5). При нарастании возбуждения, актуализации потенциальных энергий положительной и отрицательной плотности в кинетические, будет возрастать частота, сокращаться длина волн (расширение расслоения). При превращении всей потенциальной энергии в кинетические (, ,), средняя суммарная угловая скорость областей положительной и отрицательной плотности соответствуют условию =, т.е. состоянию покоя, соответствующего средней плотности и среднему объему невозбужденной массы; экстремальные значения скорости в областях положительной и отрицательной плотности равны светоподобному интервалу; расслоение достигает максимума; возбужденная масса доведена до состояния "кипения".

В этой стадии вакуум, будет подобен расслоенной сфере (одновременно растянутой и сжатой), что в условиях достижения экстремума напряжения, возможно, обеспечивает одновременный разрыв (взрыв по всему объему, или два противоположных взрыва – в направлении расширения и в направлении сжатия). Каждой точке разрыва на “синусоиде” будет свойственна свое значение скорости. Появившиеся в момент разрыва дискретные образования (локальные вихри) консервируют свою скорость как индивидуальную характеристику, а в совокупности, по всей “синусоиде”, актуализируя одновременно весь диапазон угловых скоростей, которые при математическом колебании проявляются только в последовательной форме, т.е. изолированно друг от друга. Очевидно также, что сжатые и растянутые сферические области будут разграничены сферическими областями невозбужденного вакуума со средними характеристиками плотности, объема, скорости. Аналогично, внешняя граничная сфера и область центра сферической массы “пробной вселенной” будут также представлены невозбужденным “покоящимся” вакуумом. Если в первом случае покоящийся вакуум может быть представлен особыми квантами при дальнейшем процессе образования дискретных вакуумных структур, то во втором, вакуум в чистом виде (внешняя оболочка сферы и центр) останется при любых последующих превращениях. Внешняя оболочка и центр возможно влияют на кривизну пространства, создают специфическое вакуумное поле кручений, определяя пространственную целостность возбужденного образования (абсолютной системы отсчета).

6.4. Эволюция вещества. Разрывы и процессы квантования могут происходить или при переходе от сжатия к расширению (в сферах +р) и наоборот от расширения к сжатию (в сферах –р) т.е. в экстремальных значениях плотности в момент смены направления кручений (с левого на правый и наоборот) и мгновенной остановки движения, или в состоянии равной и средней по всему объему плотности (где расслоение представлено различными угловыми скоростями в отношениях синусоидального графика), т.е. в момент изменения знака плотности энергии). Вероятно, что первая фаза разделения происходит в состоянии средней плотности, где достигается максимум кинетических скоростей и, соответственно, максимум кинетических энергий, а квантованный вакуум закрепляет равные порции массы для всех значений скорости.

В момент разрыва возможно образование симметричных вихрей с последующим взаимным захватом двух зеркальных вихрей и образованием вихревых дуплетов, или двухвихревых ”фитонов” (по А.Акимову, 22). При этом дуплеты будут закреплять собой элементы системы отсчета (осевые моменты) фиксируя присущее им в момент образования “индивидуальные” значения угловой скорости.

Дуплеты, после образования, перейдя в область противоположной плотности, продолжают инерциальное движение еще по сценарию математического маятника (несмотря на приобретенное новое качество), когда их движение определяется отрицательным бинормальным моментом, двух собственных мнимых моментов. При этом, реакция дуплета на инерциальное изменение плотности и объема может быть связана с изменением частоты колебаний (поочередного проявления, актуализации зеркальных вихрей). В областях положительной и отрицательной плотности частоты будут иметь, соответственно, положительные и отрицательные характеристики (степени, логарифмы).

Вхождение в экстремумы плотности (+p) и (-p), будет сопровождаться повышением степени возбуждения дуплета (повышением частоты смены вихрей) и может завершиться новым “разрывом”, с переменой направления и метрики моментов (с правых на левые и наоборот, с 1-мерной на 3-мерную и наоборот)) с последующим зеркальным удвоением дуплетов, т.е. с появлением “квадриг” из четырех вихрей, с актуализацией дополнительных полуосей соприкасающейся плоскости кручений, с фиксацией значений угловых скоростей, но уже в четырехвихревой “квадриге”. В захваченной вихрями части первичной материи, система отсчета будет представлена в дискретной форме (в форме периодической смены моментов кручений и поочередной актуализации элементов ортогональной системы отсчета - полуосей координатного пространства). Соединение на одной полуоси противонаправленных моментов, возможно, лежит в основе появления пространства в привычном нам представлении в форме 3-мерных трансляций. Пространство проявляется как комплексная характеристика, связанная с актуализацией мнимых моментов и соединения их с действительными моментами, с консервацией (стабилизацией) вращательного движения и актуализацией направленных трансляционных координат.

6.5. Стационарная Вселенная. Примерно по такой схеме инерциальный процесс колебаний может продолжаться несколько циклов. Границей циклов являются экстремальные значения моментов и энергии плотности. Переход границы будет связан с изменением знака моментов, или изменением знака плотности, с очередным удвоением и образованием новых, более плотно упакованных, вихревых образований (2, 4, 8,..?), с появлением качественно новых структур. Завершение многоактного процесса квантования и актуализации координатного пространства пробной массы, может соответствовать сценарию Я.Терлецкого: на одной из завершающих стадий квантования, вихри положительной плотности сворачивают вакуум в сжатые кванты, а вихри отрицательной плотности - в растянутые кванты, происходит перераспределение плотности в границах стационарного объема в форме естественного самодвижения, без "взрывов" и “разлетания в никуда”. Процесс квантования вакуума будет связан с актуализацией электромагнитных, гравитационных и торсионных (спинорных) полей, и последующим перераспределения вещества с актуализацией гравитации, пространства и времени. Инертная масса вакуума получает эквивалентное выражение в отношениях гравитации квантованных структур.

В целом, процесс квантования предстает, как способ естественного разрешения противоречий (отношений плотности и отношений кручений) в. Разрешение противоречия учреждает качественно новое состояние покоя в границах стационарной “пробной Вселенной” (абсолютного, в целом, по всему объему, но относительного для каждой локальной ИСО). В приложении этого представления к реальной Вселенной, принцип Маха можно сформулировать в обратном направлении - абсолютная система отсчета не результат механического усреднения “далеких космических масс”, а, наоборот, исходное, начальное условие вещественной эволюции, определяющее квантование абсолютной системы отсчета на многообразие ускоренных относительных систем отсчета. Суммарный эффект локальных систем отсчета соответствует исходному состоянию покоя физического вакуума, чем обеспечивается стабильность, абсолютная устойчивость, и, в конечном счете, - гармония законов природы.

Гипотеза стационарной модели Вселенной противоречит утвердившейся гипотезе расширяющейся Вселенной (А.Фридман,1929г.), подтверждаемой эффектом Доплера и красным смещением Хаббла (1929). Открытие Хаббла (постоянная Хаббла) подтверждает однородность и изотропность Вселенной, но гипотеза расширения требует более убедительной аргументации. В частности, априори очевидно, красное смещение спектра связано с отражением излучающей свет космической материи и не связано с той материей, которая поглощает свет. Иначе, вероятная ограниченность наших систем измерения позволяет видеть лишь половину процесса, свидетельствующую о расширении. Распространение половинчатого результата на всю материю приводит к серьезным заблуждениям. В рамках геометрии СТО, гипотезы расширяющейся и сокращающейся Вселенной равноправны, а в случае соблюдения симметрии относительно светоподобного интервала, - они являются составляющими гипотезы стационарной, однородной и изотропной Вселенной, в которой начальные условия покоя формулируются на равновесие плотности = (или на половинную скорость света - с/2).

Каков предел процесса квантования возбужденного вакуума? Опираясь на такие научно установленные факты как: корпускулярно-волновой дуализм, дискретная форма излучения и поглощения энергии, необратимость физических явлений (энтропия), а так же исходя из двойственной природы (инвариантность соприкасающейся плоскости и бинормали, уравнения закона сохранения абсолютных интервалов), можно предположить, что процесс квантования завершается актуализацией мнимых моментов в соприкасающейся плоскости, а энергетические взаимодействия (излучение или поглощение) связаны с периодическим проявлением моментов в соприкасающейся плоскости и моментов на бинормали (или периодической сменой относительных и абсолютных моментов). Иначе, относительные и абсолютные моменты проявляются в дискретной форме, поддерживая и сменяя друг друга. Эта открытость системы отсчета через дискретное проявление “правой” и “левой” частей закона сохранения, "дуализм", вероятно, обеспечивает энергетические обмены, связана с необратимостью процессов в физической природе, в направлении потери материей вещественной упорядоченности , приобретенной в процессе квантования вакуума.

Дуализм, оставляет открытой возможность качественно новой эволюции материи, за счет соединения двух, аналогичных по количественным характеристикам, но зеркальных, в одну систему, с одновременной актуализацией моментов соприкасающейся плоскости и базисного вектора бинормали (или относительных и абсолютных моментов), с потерей новым “дуплетом” дискретных свойств и способности энергетического обмена с внешней средой, с учреждением внутреннего, закрытого между двумя зеркальными, энергетического обмена. Дискретные свойства энтропии и энергетического обмена отдельных составляющих дуплета, вместе превратились в непрерывный процесс внутренней циркуляции энергии. С этим свойством новый дуплет выделяется из процесса необратимой энтропии, и в этом смысле приобретает вечную, неуничтожимую форму. Вполне возможно, что становление неуничтожимого кванта включает несколько фаз удвоений.

Дальнейшее движение абсолютного кванта будет теперь связываться с развивающимся противоречием (все возрастающим различием между его внутренним абсолютным порядком и внешним относительным порядком), с “бессмертием” его абсолютной формы организации, с одной стороны, и “смертностью” относительной формы организации внешней физической природы, с другой стороны. Естественное разрешение этого противоречия – в противостоянии внешней вещественной энтропии, в развертывании негэнтропийного процесса, в приведении среды в соответствии с самим собой и с организацией равновесия энтропия-негэнтропия, т.е. в учреждении метаболизма как управляемого процесса синтеза и распада.

6.6. Энтропия и физическое время в. Согласно второму началу термодинамики вещественная материя подверженная энтропии, постепенно теряет упорядоченность, приобретенную вещественной эволюцией. Потеря упорядоченности (распад) связана с логарифмической формой. В условиях, когда предложенная ИСО СТО концепция времени, имеющего ту же природу что и пространство, при ее рассмотрении в теряет смысл, действительное физическое понятие времени может быть связано с энтропией, как с периодическим процессом, что, соответственно, меняет геометрическую форму закона сохранения пространственно-временного континуума.

С теоремой Пифагора связываются только пространственные (1-мерные и 3-мерные) характеристики. Временные характеристики могут быть связаны с логарифмической структурой пространства (с логарифмом возбужденного пространства относительно некоторого основания – состояния покоя), со степенью его возбуждения (и, соответственно, с его упорядоченностью как потенциальной длительностью, временной формой существования порядка, целостности). А это значит, что теорема Пифагора и пропорциональные отношения , базирующиеся на геометрических прогрессиях и степенных рядах, в совокупности являют собою количественный базис пространственно-временного континуума.

В стационарной Вселенной, тепловая энтропия связывается с перераспределением теплоты. Суммарная температура стационарной Вселенной постоянна и равна 0 (температуре покоя, при=). В стационарной Вселенной, следствие второго закона термодинамики может быть сужено до представления об энтропии, как процессе потери вещественной материей степени своей упорядоченности (структурной организации). Это свойство уже не симметрично внутри отношения звездной материи и межзвездного пространства (масс положительной и отрицательной плотности энергий), ибо и та и другая теряют упорядоченность, и их потенциальным будущим является абсолютный бесструктурный невозбужденный, покоящийся физический вакуум.

Для вещества, как возбужденного вакуума, уровень упорядочения структуры связан со степенью возбуждения первичного вакуума. Степень возбуждения может рассматриваться как логарифм возбужденной массы по основанию массы покоя вакуума для условий стационарного объема, характеризуя тем самым некий запас (количество) вещественной (временной) прочности первоматерии. Это соответствует как второму началу термодинамики (логарифмической форме периодизации распада), так и теории информации (логарифмической форме количества упорядоченности структуры). При этом, второе начало термодинамики может рассматриваться как приложение к физической природе теории информации, а потеря неорганической материей информации и ее накопление органической материей - как две диалектически противоположные формы единого процесса движения , определяемого одним логарифмическим законом.

Потеря информации неорганической природой и ее воспроизведение в особой форме органической природой - это две стороны одного явления. Квантование материи привело к запасу организации (к потенциальной длительности существования вещественных форм), к движению, связанному с потерей физической упорядоченности. Этот же процесс побуждает обратный поток - накопление организации. Но не буквальное ее восстановление, а через отражение потерянного количества и воспроизводство этого количества но в качественно новой, органической форме организации, критерием которой является самосохранение (противодействие энтропии). Энтропия и негэнтропия в природе - не случайное, механическое отношение симметрии, а диалектическое отношение симметрии, связанное с диалектикой равновесия и покоя природы в целом.

6.7. “Абсолютный квант”, органическое время, живая материя. Диалектической альтернативой второму началу термодинамики (необратимости распада материи) в рамках стационарной Вселенной, ориентированной на равновесие (=), является обратный распаду процесс - негэнтропия, а отношение энтропия-негэнтропия должно представлять очередной естественный уровень динамического равновесия. Физическим исполнителем этого синтеза, носителем генетической программы развития, может быть “абсолютный квант”, квант, рожденный вакуумом и абсолютно актуализировавший потенциальную способность. В силу своей природы и общего принципа динамического равновесия, “абсолютный квант” должен отражать в особой динамической форме симметрию относительно состояния покоя вакуума =.

В границах рассмотренной концепции (последовательная актуализация элементов координатного пространства в локальных ИСО) возможен такой квант, в котором актуализация элементов устраняет дискретное бытие (например, корпускулярно-волновой дуализм) и учреждает временную непрерывность за счет “очередного” удвоения, исключает энергетическую, физическую причинность взаимодействий (в трактовке причинности В.С.Тюхтиным в работе “Отражение, системы, кибернетика”.-М.:Наука,1970), и создает структуру, противодействующую энтропии физической материи исключительно, за счет негэнтропийных (организационно-информационных) процессов, включая естественные физические механизмы, - зеркальную симметрию, прямые и обратные информационные связи на основе универсальных пропорциональных систем (например, числа Фибоначчи) и пространственных структур (например, непрерывной ленты Мебиуса, К.Левитин. Геометрическая рапсодия, – М.:Знание,1984 с.38-69).

Эволюция неуничтожимого с позиций естественной энтропии “абсолютного кванта”, с одной стороны, и непрерывная энтропия физической материи, как среды, в которую он погружена, с другой стороны, создают возрастающие в логарифмической зависимости отношения возбуждения, которые разрешаются развитием “абсолютного кванта”, его самосохранением за счет связывания энтропии и негэнтропии в целостный динамический непрерывный процесс синтеза и распада (метаболизм) отчуждаемого от природы вещества и присеваемого в особым образом упорядоченной телесной форме. Критерием развития является сохранение исходных “абсолютных” внутренних условий, отношений, заданных при его возникновении, проявляющихся как генетическая программа. Сложность иерархической организации его телесной оболочки, как механизма динамичного метаболизма, отражает степень энтропии физической природы, степень приспособления к ее необратимым изменениям.

Вещественная, “телесная”, форма “абсолютного кванта” в процессе его эволюции - суть присвоенная природа - результат симметрии относительной, недолговечной, разрушающейся физической материи и абсолютной, неуничтожимой материи. Способность синтезировать живое тело из “мертвой” и “вечной” материй составляет суть его естественного самодвижения в вещественной природе, от простейших форм, неотличимых от физических элементов, до сложных иерархий, включивших большие объемы физической материи в процесс непрерывного метаболизма. В своем развитии, необходимо присваивая и упорядочивая внешнюю природу, познает ее, и через ее познание, он познает себя, свои феноменальные способности.

В математическом отношении, наиболее соответствующей этим целям могла быть локальная инерциальная ИСО с отношениями “золотого сечения”, т.е. с относительными симметричными (==) угловыми скоростями: == =0,6180338875; = = 0,7861513775.

Этим угловым скоростям могут соответствовать два типа симметричных квантов (положительной и отрицательной плотности энергии) с бинормальными моментами, соответственно: = ()=== 0,3819658860;

= = = 0,6180338875

Результирующий абсолютный квадратичный интервал энергии (в отношениях для единичной массы):

[] - []=-=0,381965 +0,618033=0,999999= 1

Можно предполагать, как возможность объединения “абсолютных квантов” положительной и отрицательной плотности энергии в одну систему, так и возможность их отдельного существования и развития, когда различие знаков энергии (-p; +p), рождает две симметричных и равноправных и различных формы органической жизни и, соответственно, возможно порождает более высокие уровни равновесия и симметрии в живой природе.

Отношения (угловые скорости) нормальных, касательных и бинормальные моментов инерции составляют величины числового ряда Фибоначчи:

() или целые и половинчатые, положительные и отрицательные степени числа Ф – (…-3, -5/2, -2, -3/2, -1, -1/2, 0, 1/2 ,1, 3/2, 2, 5/2, 3…) . Ряд соответствует арифметической и геометрической прогрессиям, обладает исключительными логарифмическими свойствами, что могло быть естественным образом (например, самосинхронизация и самонастройка прямых и обратных взаимопроникающих частот на отношения “золотого сечения”) выделено “абсолютным квантом” в основу особенной, организации, при создании устойчивых, самонастраивающихся механизмов отражения и воспроизводства действительных отношений внешней среды.

Нейтрализация материального эффекта (нулевая масса покоя), выход на уровень информационной причинности взаимодействий (нейтрализация энтропии), связанной с процессами отражения степеней упорядоченности (возбуждений), обладание универсальной системой пространственно-временных отношений, выделяют “абсолютный квант” в феноменальное явление физической природы. Он может быть неожиданным материальным воплощением той начальной активной субстанции, которую объективный идеализм, в частности Георг Гегель (1770-1831), понимает под категорией “абсолютная идея” (“Энциклопедии философских наук”, 1817г.). Абсолютная идея (абсолютный дух) по Гегелю, это активное, самопорождающееся и саморазвивающееся начало субстанции как субъекта. В своем развитии абсолютная идея проходит три этапа: 1) развитие абсолютной идеи в ее собственном лоне, в стихии чистого мышления (Логика); 2) развитие абсолютной идеи в форме “инобытия”, т.е. в форме природы (Философия природы); 3) развитие идеи в мышлении и истории, в духе (Философия духа). Под развитием Гегель понимает познание абсолютной идеей самой себя. (И.Т.Фролов. Философский словарь, - М: Политиздат, 1987г).

“Абсолютный квант”, в отличие от мертвой природы, теряющей информацию, вынужден накапливать ее в форме, учреждаемого им, “живого порядка” с целью самосохранения. Целеполагание становится его атрибутивно присущим его субстанции “физическим” свойством. Время, как логарифмическая функция от умирающей природы, есть длительная, историческая, количественная мера этого порядка, свойственная различным уровням иерархии живой материи (1,8). Исходя из общей концепции, происхождение живых форм и их развитие это законный в объеме стационарной, однородной и изотропной Вселенной результат. Реализация “абсолютной идеи” возможна в любой части Вселенной, где есть вещественные условия необходимые для развертывания и организации стабильного, обеспечивающего самосохранение, метаболизма. При этом, не исключена принципиальная возможность полного включения всего вещества Вселенной в негэнтропийный процесс развития, как целостной органической формы, т.е. возможность абсолютного деятельного познания природы, через ее включение в процесс метаболизма (вплоть до тотальной, всеобщей формы).

Такой подход, вероятно может быть согласован с идеей Г.И.Шипова-А.Акимова (22, с.188-210) о потенциальной сознательной и информационной способности первичных вакуумных полей. В теории физического вакуума эта идея связывается с существенной особенностью вакуума, с существованием полей, обладающих нулевой энергией, но способных к взаимодействию. С точки зрения А.Акимова и В.Бинги, более всего на роль материальных оболочек-носителей информации претендуют первичные торсионные поля, называемые информационными полями. В концепции Татура, в основу физической картины мира положены три субстанции – аксионные поля, слабая метрика и Отображения, которые обеспечивают такие свойства материи, как самодвижение и целостность. Аксионные поля – поля сверхлегких частиц, которые отображают мир элементарных частиц - каждую элементарную частицу сопровождает свойственное ей поле. Со слабой метрикой связывается параметрическое пространство, в котором нет протяженности. Субстанция Отображения определяет монадные свойства слабой метрики и является источником самодвижения материи. Отображение между элементами слабой метрики приводит к кручениям. Существует две группы отображений, порождающих правые и левые пространственно-временные вихри. Отображение, кручение пространства более фундаментальны, чем время (22,с.188-210).

Если говорить о том, что абсолютный квант является специфической ИСО (базирующейся на основе), и что его самосохранение связано с воспроизводством своей пространственно-временной формы посредством отражения внешней среды, естественно полагать, что кроме натуральной геометрии пространства унаследованной с, он должен иметь в своем распоряжении универсальный логарифмический механизм отражения, коммуникации, преобразования и представления информации, функционирующий в режиме прямых и обратных связей.

Этот механизм должен быть связан, как с действительной физической геометрией – теоремой Пифагора, так и с информационной (логарифмической) системой пропорциональных отношений (рис.6.). Это условие осуществимо, наряду с другими отношениями на синусоидальном графике скоростей, при двух, симметричных относительно состояния покоя =, угловых скоростях на осях моментов в соприкасающейся плоскости =; = или =; =. При этом квадратичные скорости бинормальных моментов будут равны ()=; ()=; ()=; ()=;

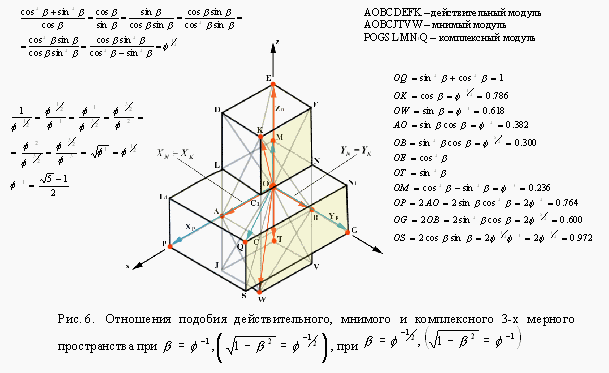
Относительные (угловые) скорости моментов инерции составляют величины ряда Фибоначчи: (или целые и половинчатые, положительные и отрицательные степени числа Ф – …-3, -5/2, -2, -3/2, -1, -1/2, 0, 1/2 ,1, 3/2, 2, 5/2, 3…). Иначе, все отношения кручений здесь определяются отношениями “золотого сечения” - уникальным числовым рядом, сочетающим арифметическую и геометрическую прогрессии, имеющем оптимальную логарифмическую структуру и обладающим переносной, поворотной и зеркальной симметрией, (рис.6). Приведенное в начале обсуждения высказывание Кеплера, по существу указывает на ключевые отношения пространства-времени: теорема Пифагора - геометрия пространства, среднепропорциональные (логарифмическое) отношения – геометрия времени. Синтез геометрий пространства и времени в системе уравнений порождает особую геометрию отношений, связанную с числами Фибоначчи (золотое сечение) (4,6).

Проведенное исследование геометрии физического пространства позволяет установить наличие еще не реализованных в практике и теории естествознания идей геометрической упорядоченности материи, связанных с применением принципа симметрии, и обладающих большими конструктивными возможностями для моделирования физических явлений. Так как цель настоящего рассмотрения связана с общей проблемой геометрии и гармонии в природе и затрагивает различные сферы знаний, предложенные в тексте математические конструкции и схемы представлены в черновой, упрощенной форме (в качестве грубой иллюстрации математического содержания развиваемой философско-математической концепции) и требуют дальнейшей специальной разработки.

Являясь непротиворечивой в своей основе, развиваемая концепция предполагает уточнение ряда утвердившихся в физике, математике и философии понятий и категорий (светоподобный интервал, инерциальное движение и самодвижение, пространственно-временной континуум, теория мнимых и комплексных чисел, математическое и физическое определение точки, теория логарифмов и т.д.). так же предлагает широкие конструктивные возможности в моделировании разнообразных процессов в природе (органическая и неорганическая эволюция, информационная и физическая причинность взаимодействий, процессы отражения информации живыми системами и т.д.).

Главная страница